基于自適應未知輸入觀測器的多故障快速重構
高 升, 馬廣富, 郭延寧,*
(1. 哈爾濱工業大學航天學院, 黑龍江 哈爾濱 150001; 2. 中國科學院沈陽自動化研究所, 遼寧 沈陽 110016)
0 引 言
現代工程系統變得越來越復雜的同時,人們對高可靠性和安全性的需求也日益增加。由于系統經常受到各種類型的外部環境的影響,導致系統易發生故障,從而影響系統的可靠性,甚至出現系統崩潰的情況。因此,及時地發現故障并定位故障就顯得尤為重要。近10年來,現代工程系統的故障診斷技術已成為一個重要且熱門的研究課題,并已成功應用于航空航天系統、工業機器人系統、水下航行器系統等。
故障在實際工程中是非常常見的,而故障診斷的目的便是檢測故障的發生,并進一步確定其位置。在最近的一篇綜述文章中,故障診斷方法被分為4類,即基于解析/數學模型的方法、基于信號的方法、基于知識的方法和混合方法。基于模型的方法是研究最早、成果最多的方法,其中基于觀測器的故障診斷方法更是受到學者們的青睞,也得到了大量應用。Tan等人指出,基于觀測器的故障診斷就是將系統的輸出與基于系統模型設計的觀測器的輸出進行比較,形成殘差,并將其作為故障診斷的依據。雖然該方法和生成的殘差可以用于檢測和定位故障源并產生警報信號,但不能提供故障幅度的信息。因此,需要應用故障重構方法進一步提供更深層次的故障信息。
近年來,基于觀測器的故障重構研究成果頗豐,如自適應觀測器(adaptive observers, AO)、未知輸入觀測器(unknown input observers, UIO)、滑模觀測器(sliding-mode observers, SMO)、神經網絡觀測器(neural-network observers, NNO)和廣義系統觀測器(descriptor system observers, DSO)等。文獻[11-12]針對非線性系統設計UIO將系統未知輸入干擾與故障完全解耦,從而達到故障重構的目的,但其主要問題是需要滿足觀測器匹配條件,許多實際系統難以滿足。文獻[13]針對非線性系統設計SMO完成系統的故障重構任務,當擾動和故障分布矩陣滿足一定條件且抖振效應可以忽略時,該方法可以獲得較高的故障重構精度。基于NNO的方法也可以達到故障重構的目的,但其參數的隨機性在一定程度上限制了其應用。Gao等人提出一種基于廣義觀測器的故障重構方法,該方法將傳感器故障與系統狀態向量組合構建增廣系統,從而達到多故障重構的目的,但其未考慮測量噪聲對故障重構結果的影響。
在過去的幾十年里,許多學者對基于AO的故障重構方法進行了研究,并在非線性系統中取得了一些重要的成果。這些方法考慮了傳統AO中固有的嚴格正實(strictly positive real, SPR)假設條件,這比觀測器的匹配條件更為保守。Zhang等人基于優化的思想設計了一種快速AO以提高故障重構的性能,并拓寬了AO的應用范圍。文獻[19]采用AO來重構故障,該方法需要知道故障與故障導數的上界。
為了進一步改善AO的估計性能及應用范圍,學者們圍繞自適應UIO (adaptive UIO, AUIO)進行了大量的研究工作,得到了豐富的研究成果。起初是在UIO的基礎上引入自適應算法,用于估計常值的或者隨時間變化的未知參數故障,達到故障檢測與隔離的目的。然后,為了進一步實現執行器故障和傳感器故障的同時估計,學者們將傳感器故障視為一種增廣狀態,在此基礎上設計AUIO完成多故障估計任務。文獻[22-23]提出了可用于非線性系統魯棒故障估計的AUIO,但沒有考慮故障估計的性能,即故障估計的快速性問題。文獻[24-26]雖然考慮了故障估計的性能但未考慮測量噪聲對重構結果的影響。與此同時,這些研究成果均未考慮執行器故障耦合于非線性函數的情況。
基于上述分析,本文提出一種基于AUIO的多故障快速重構方法(fast AUIO, FAUIO),該方法同時考慮了未知輸入干擾和測量噪聲干擾,并能同時重構系統中的執行器故障和傳感器故障。與已有方法相比,本文創新性地考慮一類非線性函數中耦合執行器故障的非線性系統,并設計相應的執行器故障解耦方法。為了盡可能達到魯棒故障重構的目的,本文基于優化的思想設計H性能指標,通過線性矩陣不等式求解所設計的快速自適應未知輸入觀測器參數。最后,將本文方法應用于單關節柔性機器人算例,實現了一類非線性系統的多故障重構,驗證了該方法的有效性。
1 問題描述
考慮下面帶有執行器故障和傳感器故障的非線性動態系統,其中執行器故障耦合于非線性函數中:
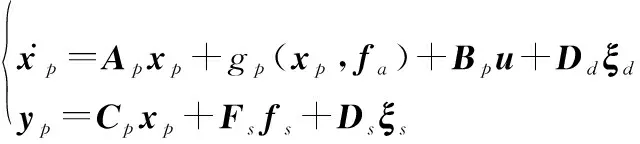
(1)
式中:∈,∈,∈分別表示系統的狀態向量、測量輸出向量和控制輸入向量;∈表示未知輸入干擾;∈表示測量噪聲干擾;∈和∈分別表示系統的執行器故障和傳感器故障;(,)表示系統的非線性函數;∈×,∈×,∈×,∈×,∈×,∈×是已知的適維常矩陣,并假設矩陣和為列滿秩矩陣。
不失一般性,對非線性函數(,)做如下分解:
(,)=+,2(,)
(2)
式中:是已知的適維常矩陣且列滿秩。
系統是可觀測的,即(,)可觀。
未知輸入干擾和測量噪聲干擾有上界但未知,的一階導數存在且有界,即
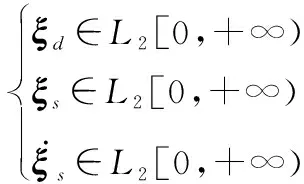
(3)
,2(,)為Lipschitz非線性項, 滿足
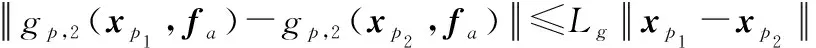
(4)
式中:為Lipschitz未知常數。
執行器故障中的元素都是連續可微函數,即可定義為時間的多項式函數,滿足
()=+++…+-1-1
(5)
式中:=1,2,…,;是未知的常數且已知;=1,2,…,-1。
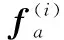
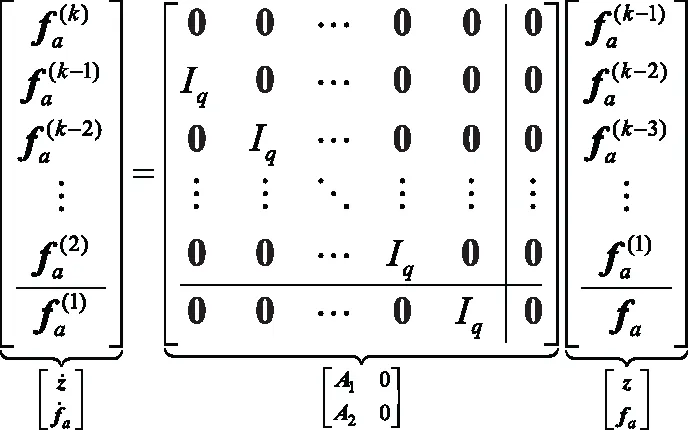
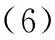
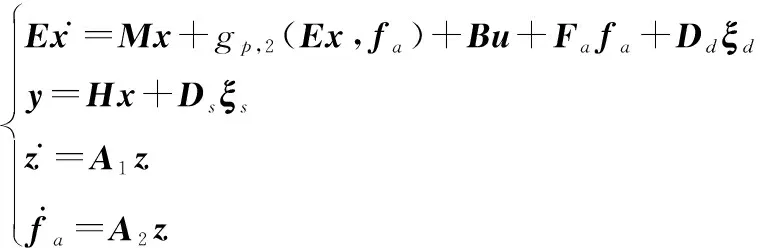
(7)
式中:=[,×];=[,×;=[,];=。
顯然,新的增廣狀態向量包含傳感器故障。因此,如果可以為系統設計一個有效的觀測器,則可以直接得到執行器故障(解耦于非線性函數)和傳感器故障的準確估計。
2 多故障重構觀測器設計
針對增廣系統,考慮如下形式的FAUIO:
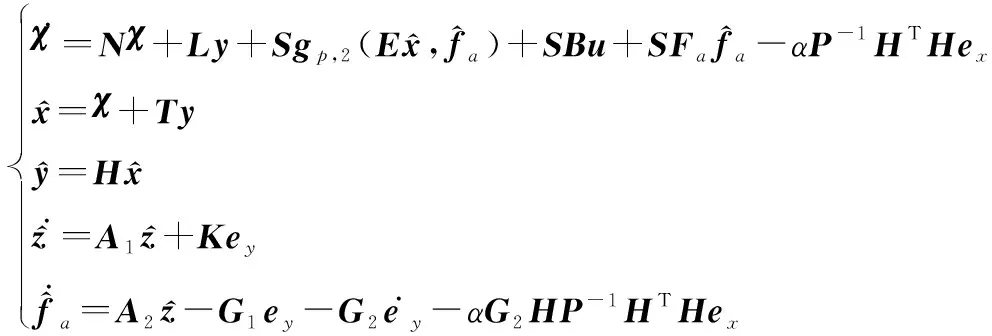
(8)
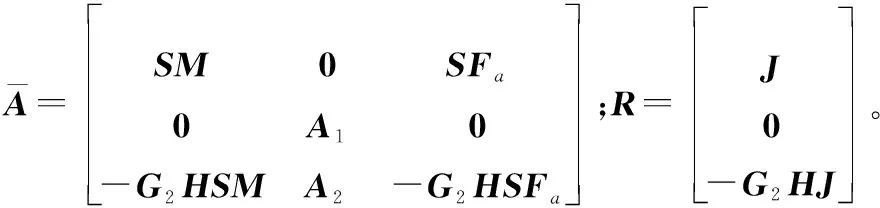
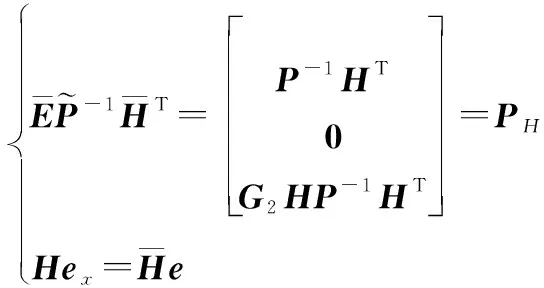
其中,根據文獻[12]和文獻[23]給出的結論,矩陣,,和應滿足如下等式:
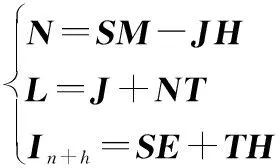
(9)
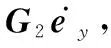
因為矩陣[,]是列滿秩矩陣,因此逆矩陣([,][,])存在,令
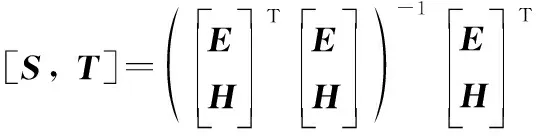
(10)
因此,式(9)中的等式+=+成立。
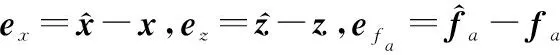
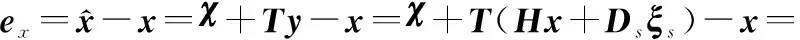
(11)
進一步可以得到
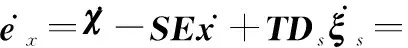
(12)
由于=-和=+成立,因此有
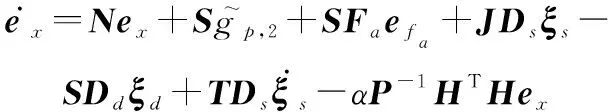
(13)
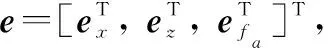
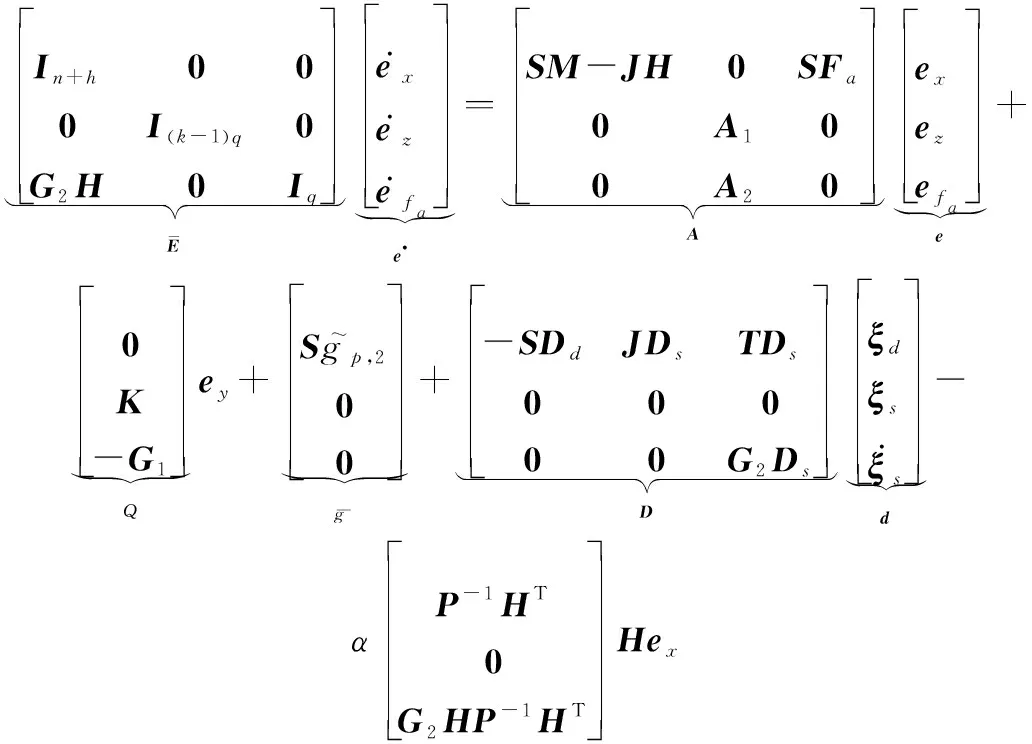
(14)
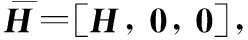
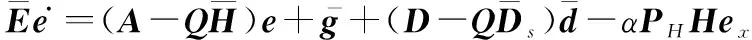
(15)
其中,
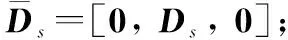
=[(),, ()]
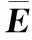
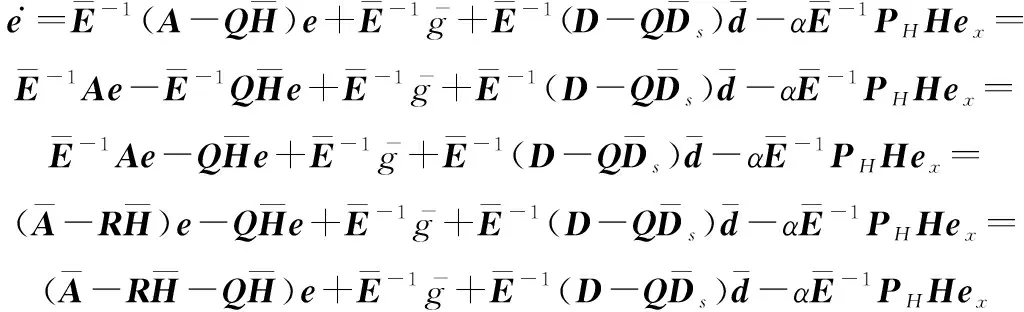
(16)
其中,
針對滿足假設1~假設4的非線性系統,設計FAUIO,如果存在對稱正定矩陣和矩陣,,和以及干擾抑制參數使得如下的LMI優化問題存在可行解:
min
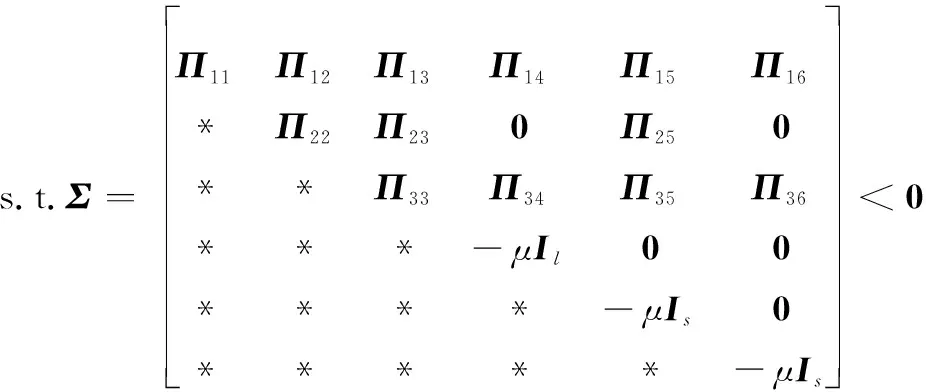
(17)

定義Lyapunov函數為
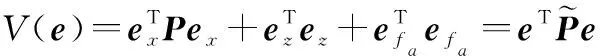
(18)
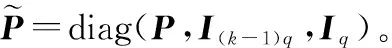
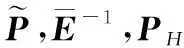
(19)
因此,估計誤差動態系統可表示為
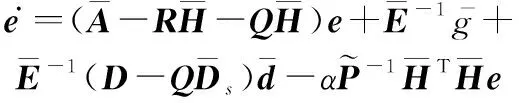
(20)
進一步對()沿著誤差動態系統求導可得
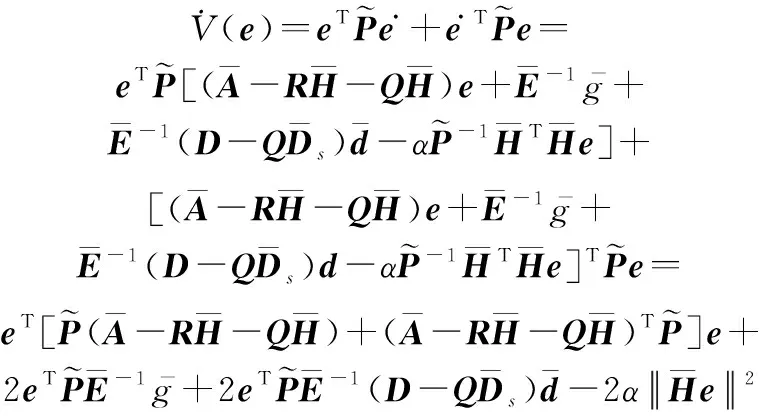
(21)
因為,2(,)是Lipschitz非線性項,因此有
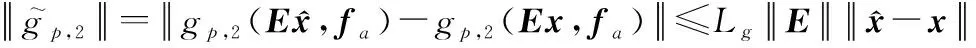
(22)
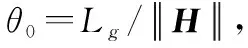
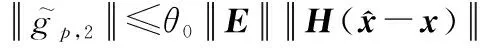
(23)
應用不等式+≤+2,可以得到:
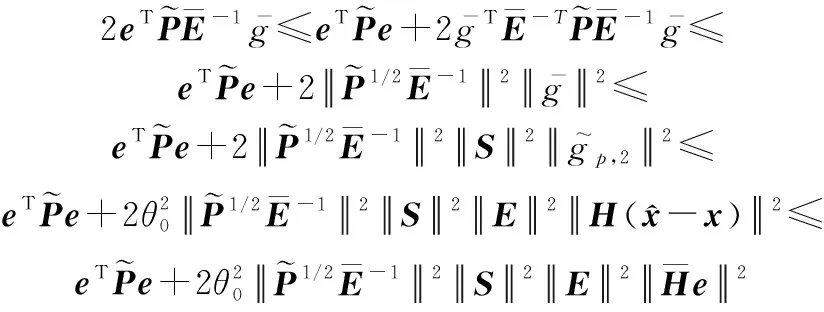
(24)
如果式(8)中的參數滿足:

(25)
有
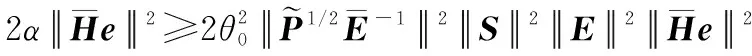
(26)
則式(24)可進一步變為
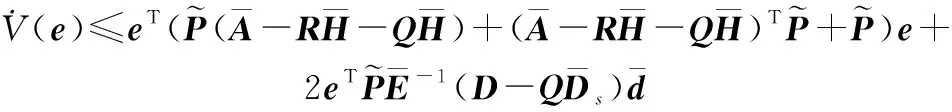
(27)
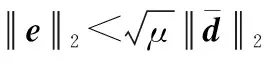
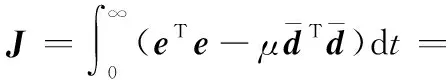
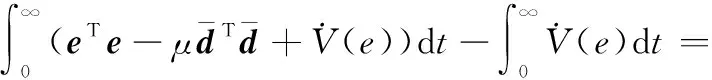
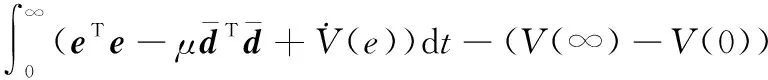
(28)
假設(0)=,因此有:

(29)
又因為(∞)>0成立,則可以求得
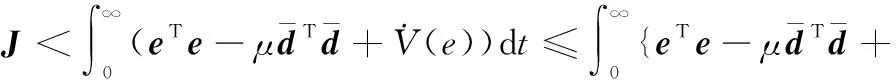
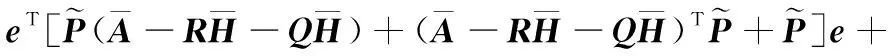
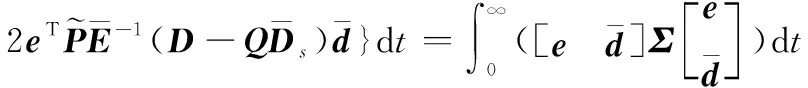
(30)
其中
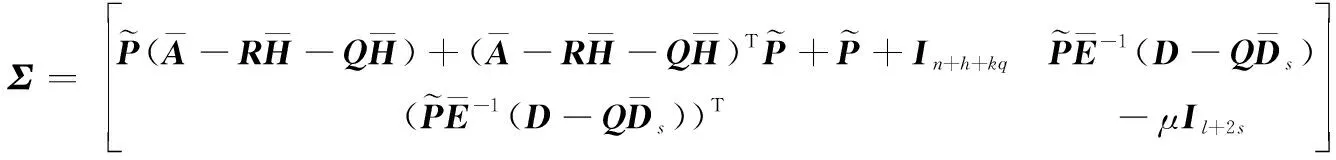
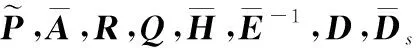
證畢
因為式(17)存在非線性項,屬于非線性矩陣不等式,不便于求解,因此需要將其轉化為線性矩陣不等式(linear matrix inequality, LMI),然后應用Matlab的LMI工具箱進行求解。因此,給出如下引理和定理用于求解LMI優化問題。
給定矩陣=,以及適維矩陣,和,則
++<
(31)
對任意滿足≤的成立的充分必要條件為存在常數>0,使得
+ε+<
(32)
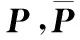
min
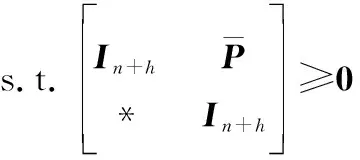
(33)

(34)
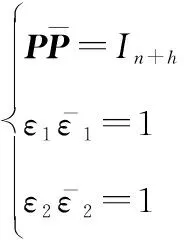
(35)
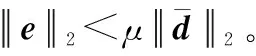
令=,則式(17)可重新表示為
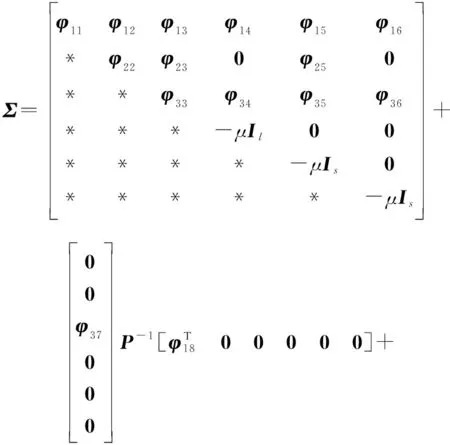
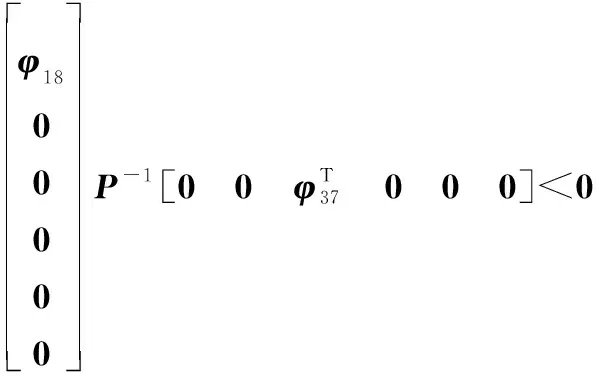
(36)
令正定矩陣滿足≤+。因此,利用引理1可以得到一個標量>0,使不等式滿足
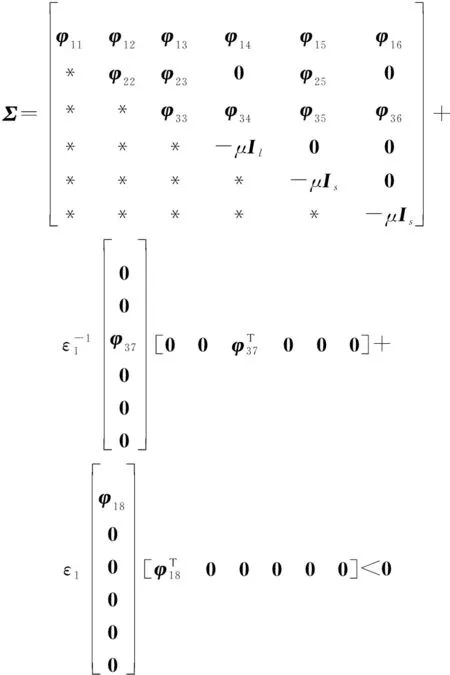
(37)
根據Schur補定理,式(37)等價于式(38),≤+等價于式(39)。

(38)
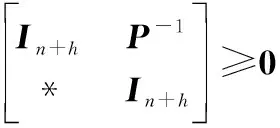
(39)
進一步令=[()],則式(38)可重新表示為

(40)
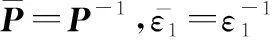
證畢
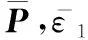
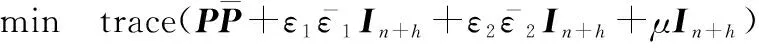
s.t. 式(33)、式(34)以及
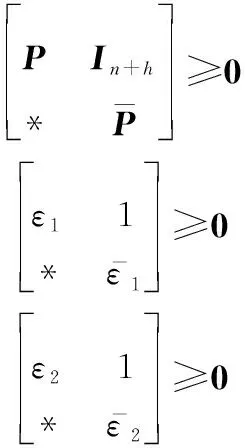
(41)
式(41)的求解過程可參考文獻[17],這里不再贅述。
3 多故障重構
若由式(41)所描述的優化問題有解,則可以通過式(1)同時完成非線性系統中執行器故障和傳感器故障的重構,即非線性系統的多故障重構任務。
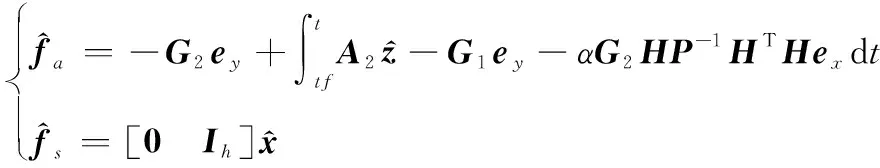
(42)
下面給出觀測器進行多故障重構的具體流程:
首先將原始系統構造成如式(7)所示的增廣系統;
應用式(10)求解得到觀測器增益矩陣和;
使用文獻[17]設計的優化迭代算法解算式(41)描述的優化問題,從而得到觀測器增益矩陣,,和=;
根據式(9)計算求得其他觀測器增益矩陣和;
最后應用所求得的FAUIO在式(42)的引導下重構執行器故障和傳感器故障。
4 算例仿真
為進一步驗證本文所提出的基于FAUIO的非線性系統多故障重構算法的有效性與可行性,以文獻[13]給出的單關節柔性機器人算例進行仿真分析,其非線性動力學方程表示為
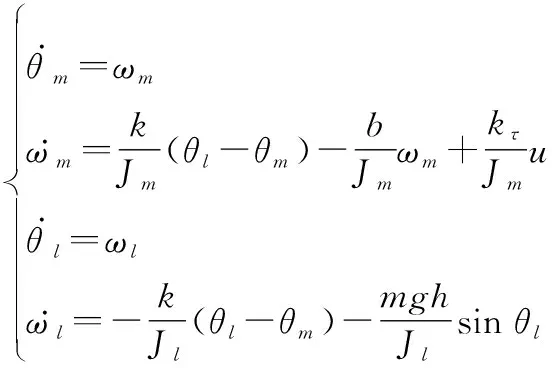
(43)
式中:,,和分別表示電機位置、電機速度、連桿位置和連桿速度。
式(43)的相關參數定義見文獻[20]。與此同時,定義系統狀態向量為=[,,,]。因此,可以得到系統的矩陣分別為
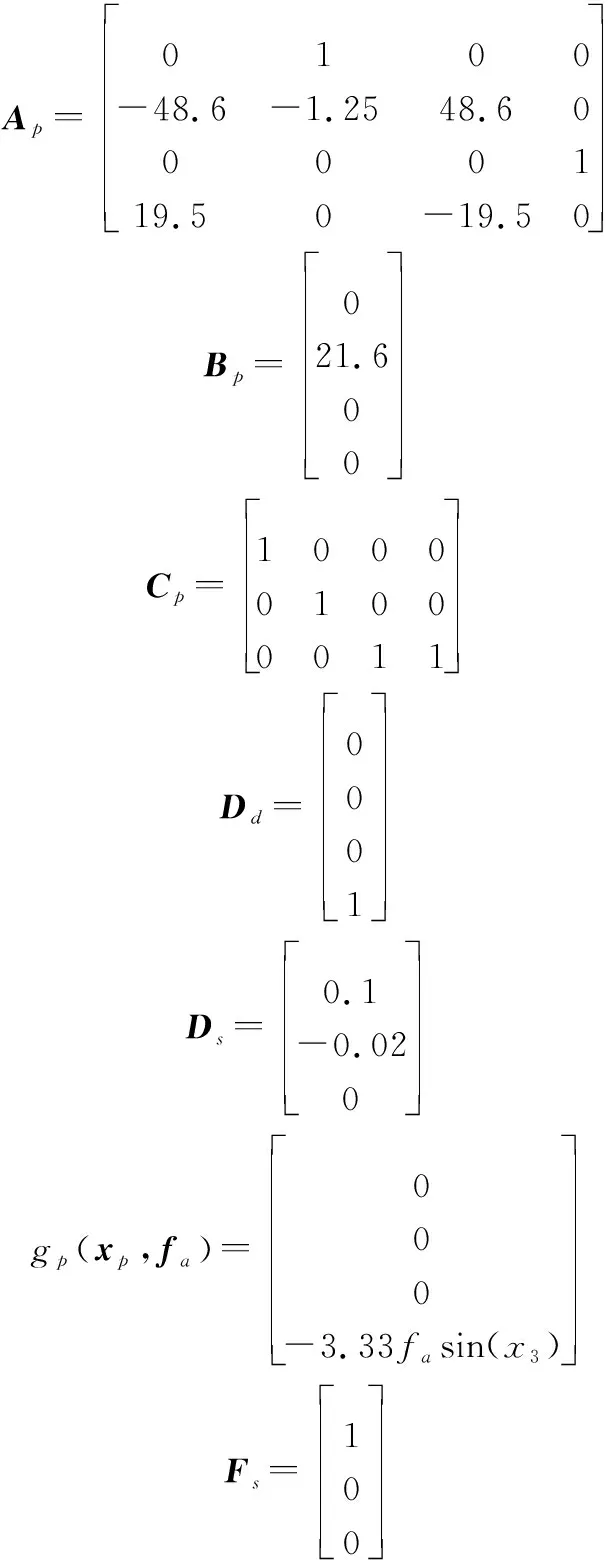
系統的未知輸入干擾及測量噪聲干擾分別定義為=02sin(10)和=01sin(10)。
與此同時,系統的控制輸入和狀態向量的初始值分別為=2sin(2π)和(0)=[0, 0, 0, 0]。觀測器的初始狀態也都為0。
最后給出系統的傳感器故障(漸進故障)和多項式形式的執行器故障(漸進故障):
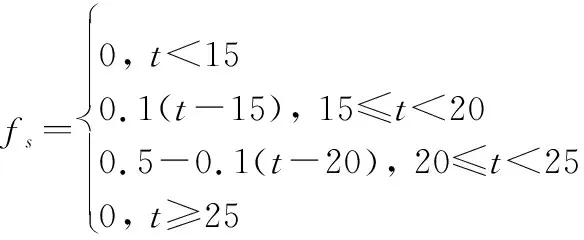
=01(-3)·(-3)-01(-8)·(-8)
式中:()為Heaviside單位階躍函數。
首先根據式(10)求得觀測器增益矩陣和為

接著應用LMI工具箱求解由式(41)描述的非線性優化問題,得到觀測器的相關設計參數分別為
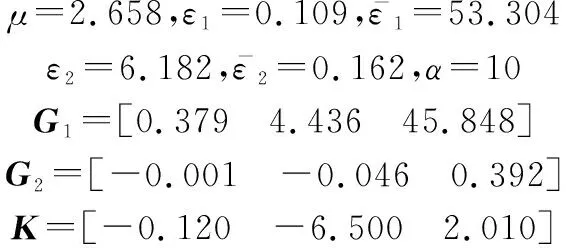



考慮到空間的限制,這里只給出系統部分狀態向量和其重構值曲線,如圖1和圖2所示,圖3和圖4表示系統執行器故障的重構值和重構誤差值曲線,圖5和圖6表示系統傳感器的重構值和重構誤差值曲線。從圖1和圖2可以看出本文提出的FAUIO能夠迅速跟蹤系統的狀態且跟蹤精度較高。從圖3~圖6可以看出,本文提出的基于FAUIO的多故障重構策略可以同時重構系統執行器故障(耦合于非線性函數中)和傳感器故障,且重構精度和魯棒性能都符合預期的設計要求。
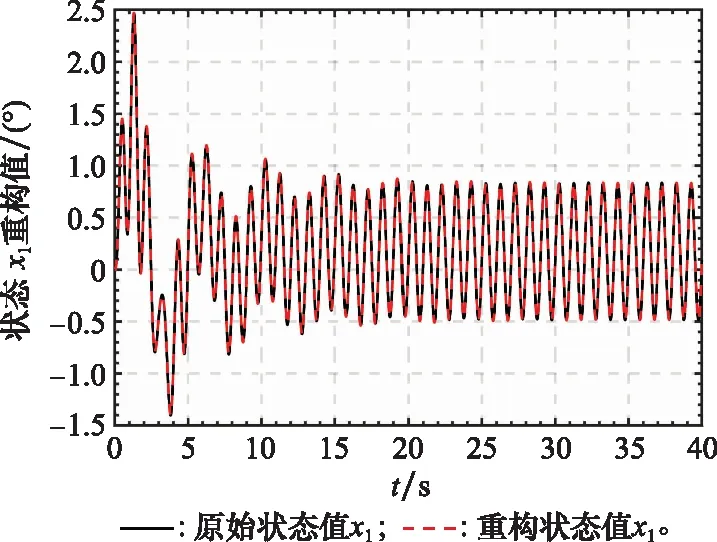
圖1 系統狀態x1和x1的重構值Fig.1 System state x1and its estimated value
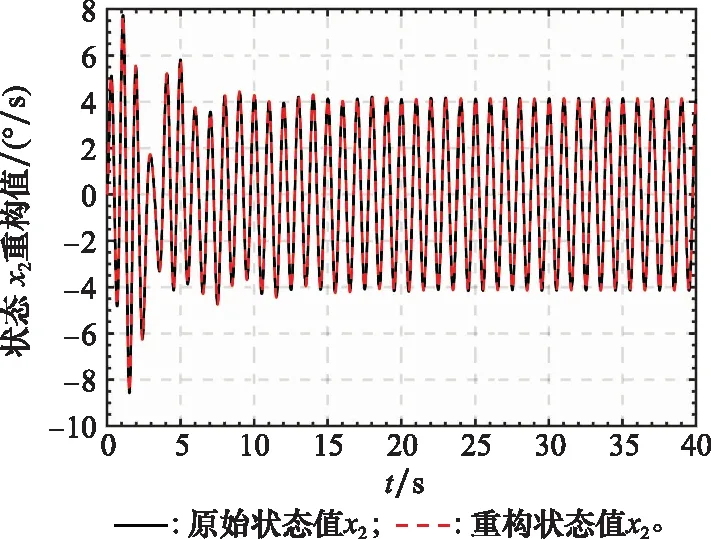
圖2 系統狀態x2和x2的重構值Fig.2 System state x2 and its estimated value
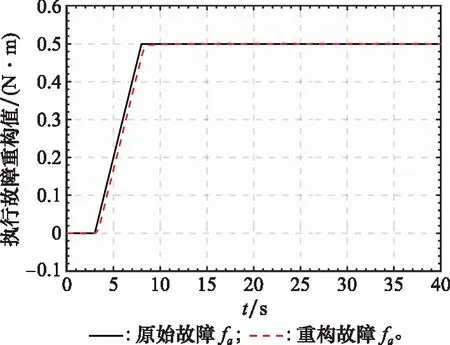
圖3 執行器故障fa和fa的重構值Fig.3 Acurater fault fa and its estimated value
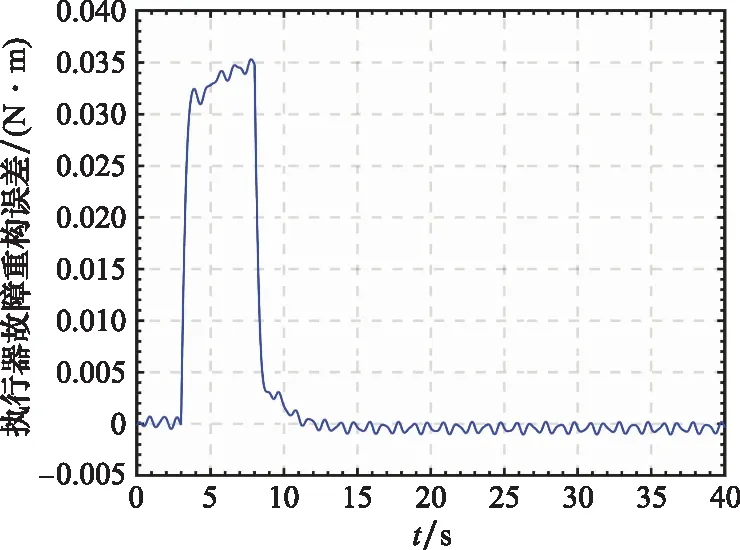
圖4 執行器故障fa的重構誤差值Fig.4 Acurator fault fa estimation error
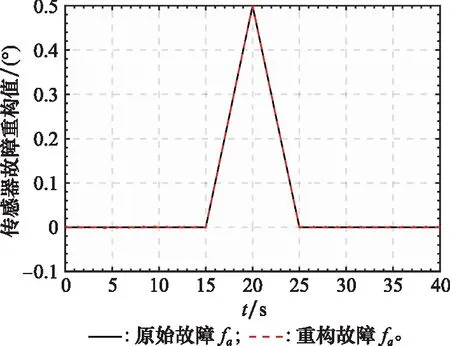
圖5 傳感器故障fs和fs的重構值Fig.5 Sensor fault fs and its estimated value
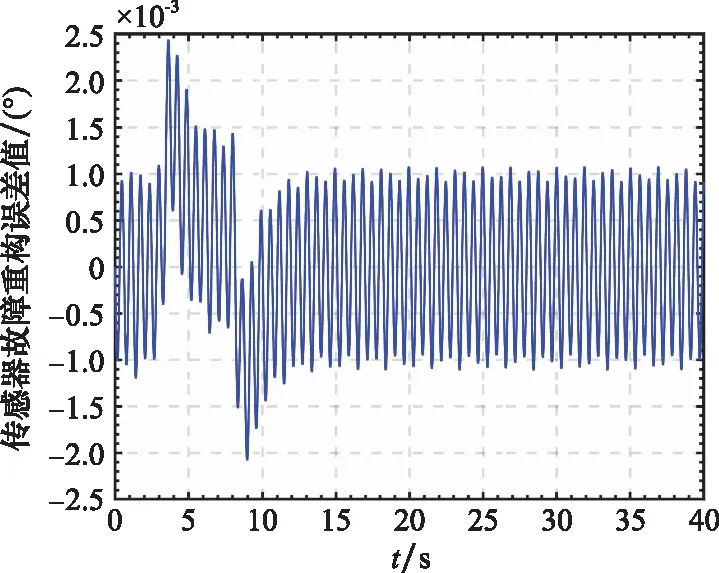
圖6 傳感器故障fs的重構誤差值Fig.6 Sensor fault fs estimation error
為了進一步說明本文所提出FAUIO的優越性能,將其與文獻[18]中提出的傳統自適應觀測器,即AO和文獻[23]中提出的自適應未知輸入觀測器,即AUIO進行了比較。同樣,考慮到空間的限制以及傳統AO不能用于估計系統傳感器故障,這里只給出執行器故障重構結果的對比分析,如圖7和圖8所示。此外,為了定量地分析仿真結果,采用故障估計誤差的均方根值(root mean square of the estimation error, RMSE)來評估不同觀測器估計不同類型故障時的準確性,如表1所示。同時,采用穩定時間,即估計誤差收斂至穩定態時所花費的時間,以此來評估不同觀測器估計不同類型故障時的快速性,如表2所示。
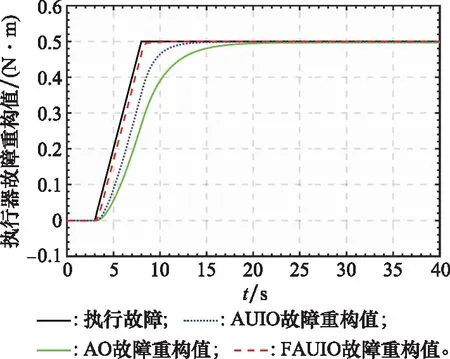
圖7 執行器故障fa重構對比結果(漸進故障)Fig.7 Comparison of actuator fault faestimation results (a ramp-type fault)
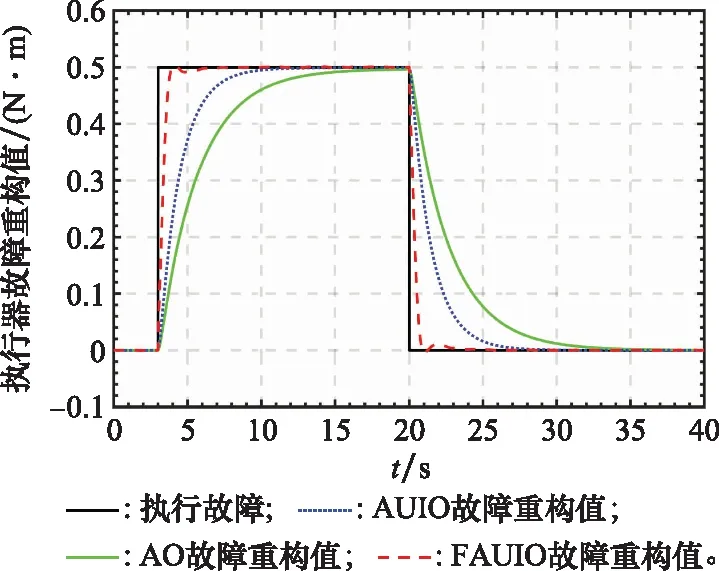
圖8 執行器故障fa重構對比結果(突變故障)Fig.8 Comparison of actuator fault fa estimation results (a pulse-type fault)
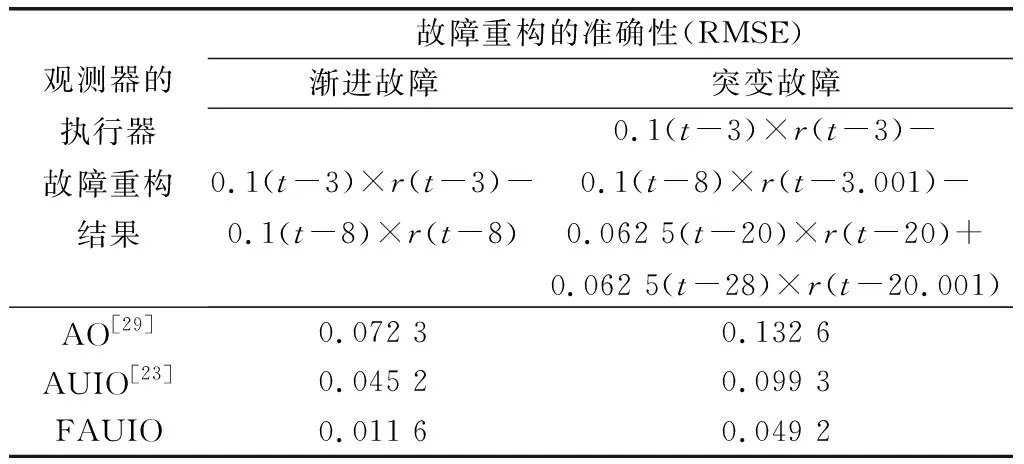
表1 觀測器重構不同類型故障時的RMSE指標
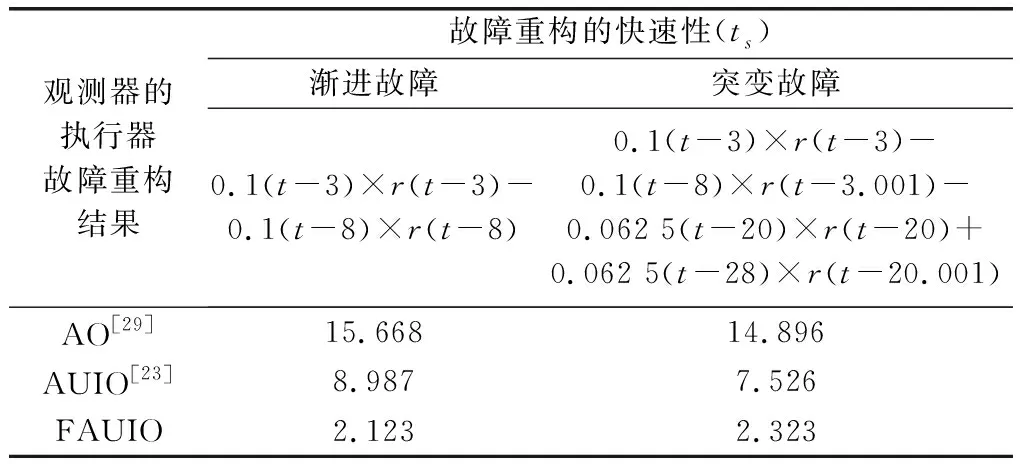
表2 觀測器重構不同類型故障時的穩定時間ts指標
由上述仿真結果可以看出,不論是在定性評估方面(見圖7和圖8所示結果),還是在定量評估方面(見表1和表2所示結果),本文提出的FAUIO重構不同類型故障時的準確性和快速性都優于傳統的AO和AUIO。因此,本文提出的FAUIO的故障重構性能得到了充分驗證。
5 結 論
本文提出了一種基于AUIO的非線性系統多故障重構策略,實現了系統中執行器故障和傳感器故障的同時重構。利用性能指標同時削弱了未知輸入干擾和測量噪聲對重構結果的影響。通過引入比例項提高了故障重構的快速性。與已有方法相比,本文創新性地考慮了一類非線性函數中耦合執行器故障的非線性系統,設計執行器故障解耦方法并成功實現了故障重構。最后,將本文提出的FAUIO應用于單關節柔性機器人系統,仿真算例結果驗證了所提方法的有效性。
將本文提出的FAUIO拓展到更復雜的系統中,如T-S模糊非線性系統、馬爾可夫跳躍系統和時滯系統,以及在考慮系統的穩定性、魯棒性、可靠性和控制性能的同時,將FAUIO的故障估計結果應用于不確定非線性系統的容錯問題研究將是下一步重點研究的內容。

