任意分布的冷備表決系統可靠度求解

胡聽春, 孫宇鋒, 李肖肖, 趙廣燕

(北京航空航天大學可靠性與系統工程學院, 北京 100191)

0 引 言

為提升系統的容錯性和可靠性,一種常見的設計是增加冗余備件,帶個冷備件的k/n(G)表決系統是一種重要的冗余設計,記作k/n:M(G)冷備表決系統。冷備表決系統結構與運行邏輯較為復雜,其可靠度求解多采用仿真法獲得,需借助軟件建模或編寫仿真程序,而解析法則更具有通用性、快速性和易實現性。因此,研究冷備表決系統可靠度解析公式具有實際意義。

k/n(G)表決系統屬于熱儲備系統。傳統的表決系統各部件多采用同型單元,然而在實際工程應用中,由于單元件的選用、采購不一致,維修換件等情況,以及復雜機電產品的發展,非同型單元組成的系統有實際的使用背景。而同型表決系統可看作非同型表決系統的特殊情況,其可靠性已有廣泛的研究成果。文獻[8]分別利用最小路集法和狀態空間法對非同型表決系統可靠度進行了解算。

冷備件在儲備時不消耗功率,在功率和維修資源有限的情況下,系統通常設計有冷儲備冗余。對于部件獨立同分布的冷備系統,其可靠度分析通常采用狀態空間法, 但狀態空間法對于大型系統都存在狀態爆炸的問題。文獻[13]利用馬爾可夫模型描述指數分布系統。文獻[14]建立了考慮故障序列直接求解系統可靠度的方法。文獻[15]提出了一種基于計數過程的解算方法。文獻[16-19]應用該方法解算各類冗余系統可靠度,簡化了求解的復雜度。以上工作均針對部件服從同一分布的系統。

表決和冷儲備模型,普遍存在于工業和軍事領域中,如電力、電子、機械、航空航天等。為保障任務可靠性需求,系統往往由表決模型和冷儲備模型組合而成,屬于冷、熱儲備混合冗余策略。k/n:M(G)冷備表決系統的定義為:系統中有個部件執行中取表決邏輯,且額外存在個冷備件。文獻[23-28]研究了具有一個冷儲備件的同型k/n:M(G)系統。文獻[29]針對帶兩個冷儲備件的同型k/n:M(G)系統剩余壽命進行分析。文獻[30]利用馬爾可夫模型研究了冷、熱備的混合備用策略的可修k/n(G)系統。以上研究均只考慮了一種儲備件替換策略,文獻[31]研究了部件獨立同指數分布的3/5:2(G)冷備表決系統,提出了備件的兩類不同的替換策略。

針對以上研究現狀,發現存在以下不足:① 現有對于k/n:M(G)冷備表決系統的研究均針對部件獨立同指數分布的情況,沒有針對部件服從任意不同分布的的情況;② 現有研究中僅文獻[31]考慮了儲備件不同的替換策略,但未考慮工作件非同型分布的情況。因此,本文在不考慮維修的情況下,對工作部件服從非同型任意分布的k/n:M(G)冷備表決系統可靠度的進行解算。

1 k/n:M(G)冷備表決系統模型

系統模型如下:

(1) 系統中共有工作件個,備用件個,當不少于個部件正常工作時系統正常工作;令表示系統累計失效次數,則系統正常工作的條件為0≤≤+-;

(2) 系統各工作件和備用件相互獨立且僅有兩態(正常和故障);

(3) 表決器及切換裝置不發生故障,即可靠度為1,且不考慮部件切換時間;

(4) 備件在儲備過程中不發生失效或劣化。

當=,一旦系統部件失效則冷備件立刻替換,n/n:M(G)冷備表決系統等效為帶個交叉儲備的級串聯系統,記作n/n+M(G)交叉儲備系統。

當<,依據冷備件的替換原則及特征,可將冷備表決系統定義為兩類,分別定義如下:

(1) Ⅰ類冷備表決系統

初始時刻開始,當任意工作部件故障,備件立即去替換。當最后一個冷備件替換后,剩余個部件組成k/n(G)系統繼續運行,直到系統故障。

(2) Ⅱ類冷備表決系統

初始時刻系統個部件開始工作,發生失效到剩個工作件正常時,再有任意工作件故障則冷備件替換。當最后一個冷備件替換后,剩余個部件組成串聯系統運行,直到系統故障。

為便于區分備件替換策略不同的兩類系統,并與經典k/n(G)表決系統相區別,將上述兩種系統分別記作k/n:M(G1)系統、k/n:M(G2)系統。

2 n/n+M交叉儲備系統的可靠度

根據工作件的不同,將交叉儲備系統分為同型與非同型系統。在同型系統中,部件獨立同指數分布的系統可靠度解算存在一種簡化的方法,故在第2.1節單獨進行討論。服從非指數分布的同型系統與非同型系統的可靠度解算方法,在第2.2節進行討論。

2.1 獨立同指數分布n/n+M交叉儲備系統可靠度

首先,針對部件及儲備件均獨立同指數分布的n/n+M(G)交叉儲備系統進行研究。系統的壽命可看作+1個獨立同指數分布的隨機變量之和。則系統可靠度可表示為

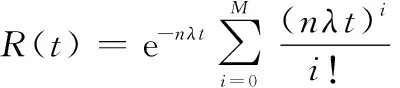
(1)

式中:表示工作件和備件的失效率。

2.2 非同型n/n+M交叉儲備系統可靠度

對于非同型n/n+M(G)交叉儲備系統,假設其個工作件服從任意不同分布,儲備件服從任意相同分布。

各組件服從非指數分布時,系統的工作過程難以用標準的隨機過程進行描述。因此,本文基于計數過程,將一個系統工作件視為一個邏輯位置。當各工作位置共享備件池且備件同型時,各工作件位置的故障過程可視為相互獨立的。

令表示在工作件位置處剛好有次失效的概率(=1,2,…,),首先需計算出系統各工作件位置發生0到+1次失效的概率,令:

(2)

令()表示在工作件位置處至少有次失效的概率,則有:

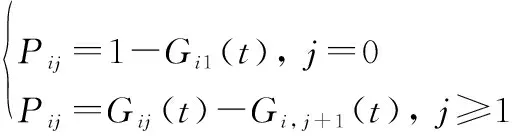
(3)

當=1時,有:

(4)

式中:()和()為系統位置(0<≤)上工作件失效概率密度函數和不可靠度函數。

當>1時,令()表示冷備件不可靠度函數,則()為, -1與()的卷積,即

(5)

n/n+M(G)交叉儲備系統正常工作的條件為0≤≤,則系統可靠度如下:

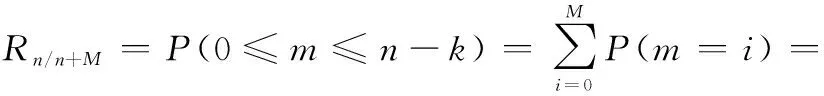
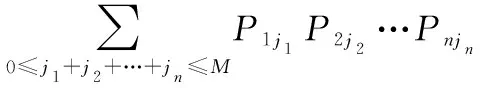
(6)

式中:(=)表示系統失效總次數為的概率,也可對概率矩陣行向量進行離散數組卷積求解。

3 k/n:M(G1)系統的可靠度

冷備表決系統分為同型與非同型系統,在同型系統中部件服從指數分布的情況同樣存在簡化的可靠度解算方法,在第31節進行討論。對于部件服從非指數分布的同型系統與非同型系統,其可靠度解算方法在第32節進行討論。

3.1 獨立同指數分布k/n:M(G1)系統可靠度

k/n:M(G1)系統壽命分為兩階段,在第一階段系統可以看作n/n+M交叉儲備系統,第二階段轉換為k/n(G)表決系統。

在第一階段,系統中任意部件故障,冷備件立即替換,系統壽命為個獨立同指數分布的隨機變量之和,則其不可靠度為

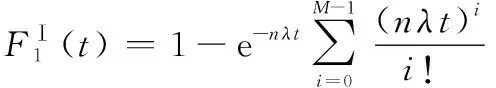
(7)

在第二階段,系統中部件故障后無備件替換,系統不可靠度使用k/n(G)表決系統公式進行求解,可表示為

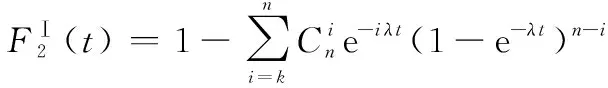
(8)

獲得不可靠度函數后,系統失效概率密度函數求解如下:

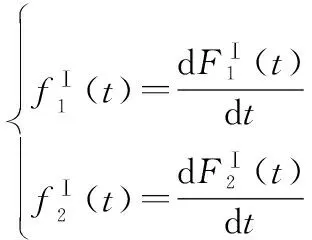
(9)

系統的工作壽命為兩階段壽命相加,則Ⅰ類冷備表決系統的失效概率密度函數為

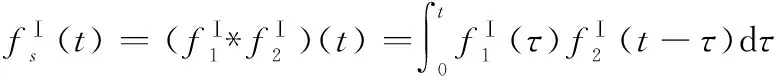
(10)

式(10)可直接求解卷積積分,也可用拉普拉斯變換法求解。系統的可靠度為

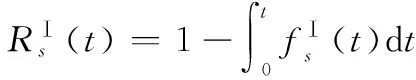
(11)

3.2 非同型k/n:M(G1)系統可靠度

對于工作件服從任意分布的非同型k/n:M(G1)系統,需分析系統正常工作時部件可能的狀態組合,稱為成功模式。考慮帶單備件的情況,k/n:M(G1)系統可能的成功模式共有1++(-1)+…+(-1)…(-)種,可表示為4類情況,如圖1所示。

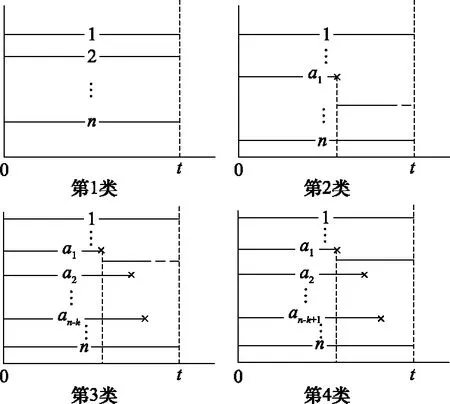
圖1 k/n:1(G1)冷備表決系統成功模式Fig.1 Successful model of k/n:1(G1) cold standby voting system

成功模式的概率之和,即系統可靠度解析式為

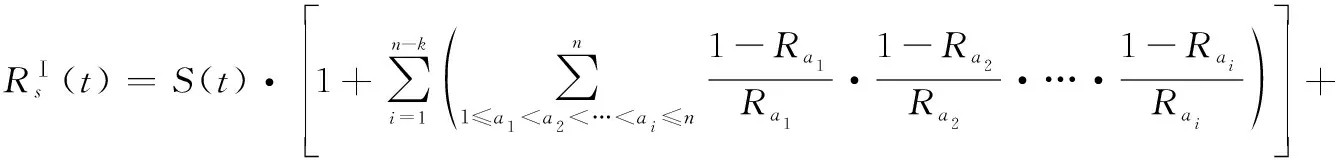
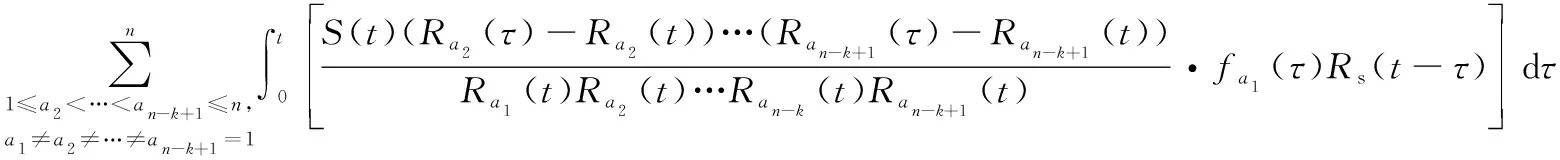
(12)

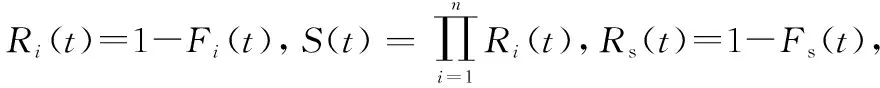
當各部件獨立同分布,系統可靠度解析式可簡化為

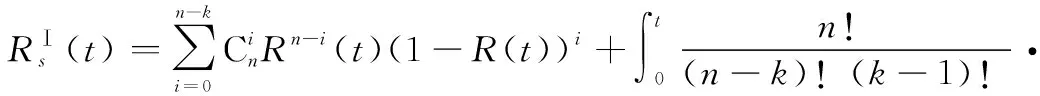
-1()(()-())-()(-)d

(13)

進一步的,當,,取任意值,k/n:M(G1)系統可靠度可表示為:=[(0個工作件故障)+…+(-個工作件故障)+(備件替換前1個位置且未故障|-+個工作件位置故障)]。

4 k/n:M(G2)系統的可靠度

第41節討論了部件獨立同指數分布的k/n:M(G2)系統可靠度的簡化計算方法,部件服從非指數分布的同型系統與非同型系統可靠度解算方法在第4.2節進行討論。

4.1 獨立同指數分布k/n:M(G2)系統可靠度

k/n:M(G2)系統第一階段可以看作k/n(G)表決系統,第二階段轉換為k/k+M交叉儲備系統。

在第一階段,系統中部件故障后備件不替換,用k/n(G)表決系統不可靠度公式表示:

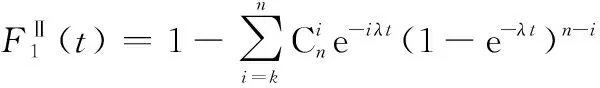
(14)

第二階段,系統中剩余部件故障后備件將進行替換,直到個冷備件耗盡,系統不可靠度表示為k/k+M交叉儲備系統可靠度:

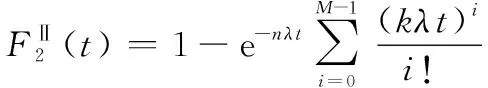
(15)

對比第31節k/n:M(G1)系統公式,k/n:M(G2)系統第一階段失效概率與k/n:M(G1)系統第二階段失效概率相等,第二階段失效概率小于k/n:M(G1)系統第一階段失效概率。因此,在系統結構與部件相同的情況下,采用Ⅱ類儲備件替換原則系統可靠性更高。

4.2 非同型k/n:M(G2)系統可靠度

對于k/n:M(G2)系統,當備件數量M為1時,與k/n:1(G1)系統相似,k/n:1(G2)系統可能的成功模式共有1++(-1)+…+(-1)…(-)種,可表示為4類情況,但備件替換的時機不同,如圖2所示。

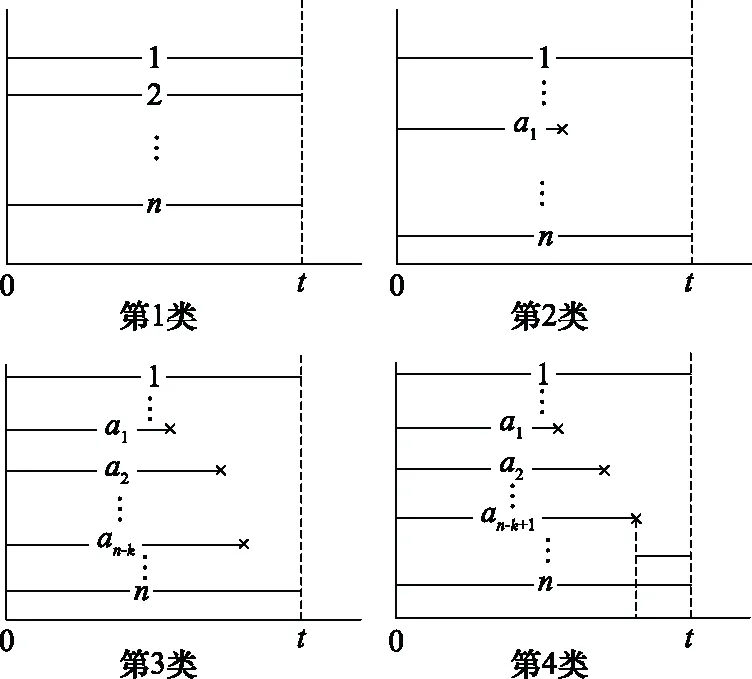
圖2 k/n:1(G2)冷備表決系統成功模式Fig.2 Successful model of k/n:1(G2) cold standby voting system

系統可靠度解析式為

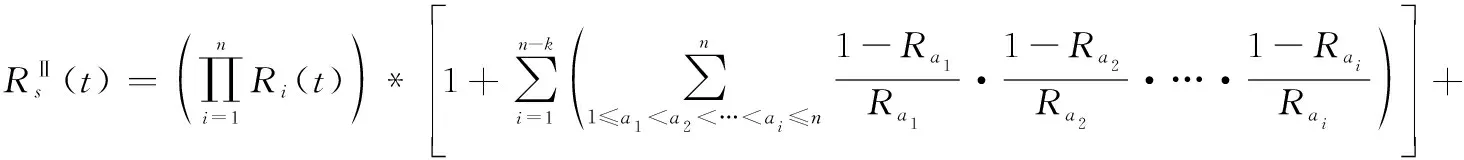
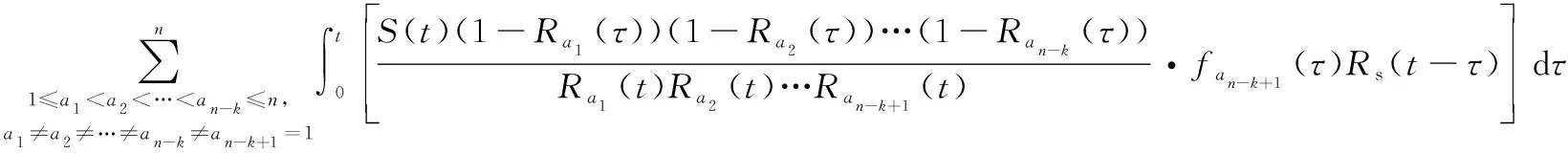
(16)

當各部件獨立同分布,系統可靠度解析式可簡化為

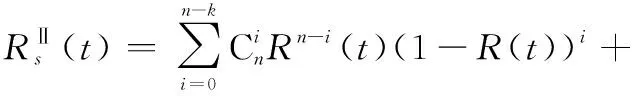
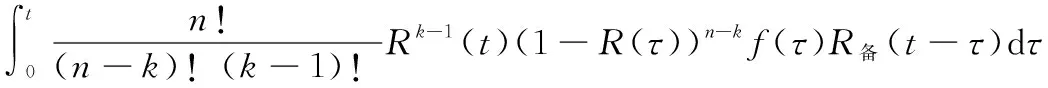
(17)

式(17)與文獻[26]中給出的同型k/n:1(G)可靠度解析式相同。

對比第3.2節非同型k/n:1(G1)系統可靠度公式,發現兩類系統解析式構型相同,不同部分存在如下關系:

(18)

因此,在系統結構與部件相同的情況下,采用Ⅱ類儲備件替換原則系統可靠性更高。

進一步推導當=-1,=2時系統可靠度,n-1/n:2(G1)系統可能的成功模式共有1++(-1)+…+2(-1)+(-1)(-2)種,可表示為5類情況,如圖3所示。

圖3 k/n:2(G2)冷備表決系統成功模式Fig.3 Successful model of k/n:2(G2) cold standby voting system

系統可靠度解析式為

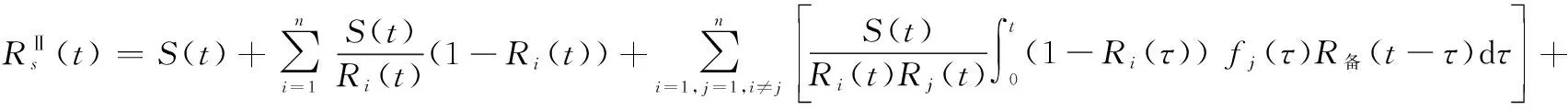
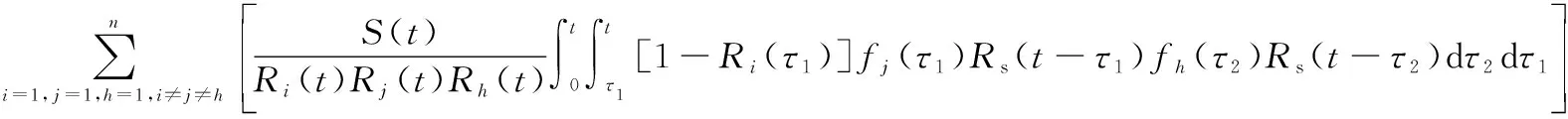
(19)

當,,取任意值,系統可靠度可表示為=[(0個工作件故障)+…+(-個工作件故障)+(至少1個備件未故障|-+1個工作件位置故障)+…+(至少個備件未故障|-+個工作件位置故障)]。

5 算例分析

在本節中,利用幾個算例,通過蒙特卡羅仿真對本文提出解析式正確性進行了驗證。利用蒙特卡羅仿真法抽樣得到系統可靠度,認為其反映真實系統可靠度。

同型35(G)交叉儲備系統

假設系統部件和儲備件均服從=001的指數分布。利用蒙特卡羅仿真獲得一個仿真解,利用第21節方法獲得一個解算解,并將卷積對象進行離散化處理(精度取1),利用第22節方法近似計算出一個解算解。將結果進行對比,如表1所示。

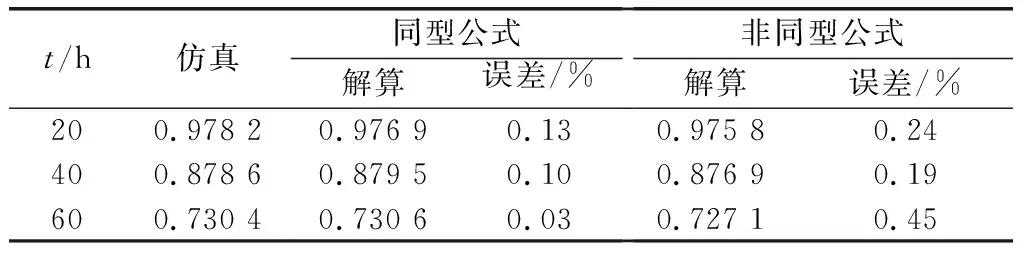
表1 同型3/5(G)系統案例結果

非同型3/5(G)交叉儲備系統

進一步驗證上述非同型n/n+M交叉儲備系統的可靠度計算方法,驗證案例的信息如表2所示。取分別為20、40、60,將仿真結果與第22節方法解算結果進行對比,如表3所示。

表2 非同型3/5(G)系統案例信息

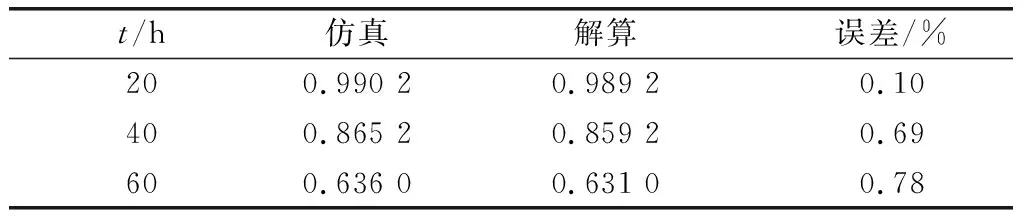
表3 非同型3/5(G)系統案例結果

同型3/5:4(G)冷備表決系統

設系統工作件和冷備件獨立同指數分布,故障率=001。對于Ⅰ類和Ⅱ類系統,時間分別取50、100、150、200,單位為h。對比利用第31節和第41節方法與仿真方法結果,如表4所示。

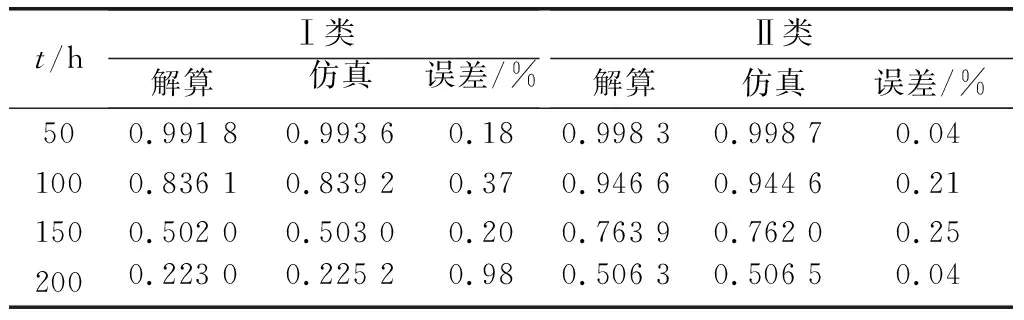
表4 同型3/5:4(G)系統案例驗證結果

非同型1/3:1(G)冷備表決系統

設系統部件服從不同的指數分布,工作件故障率取值為[,,]=[1100,1120,1150],冷備件故障率=001。取分別為50、100、150、200,單位為h。將仿真結果和第32節和第42節方法解算結果進行對比,如表5所示。

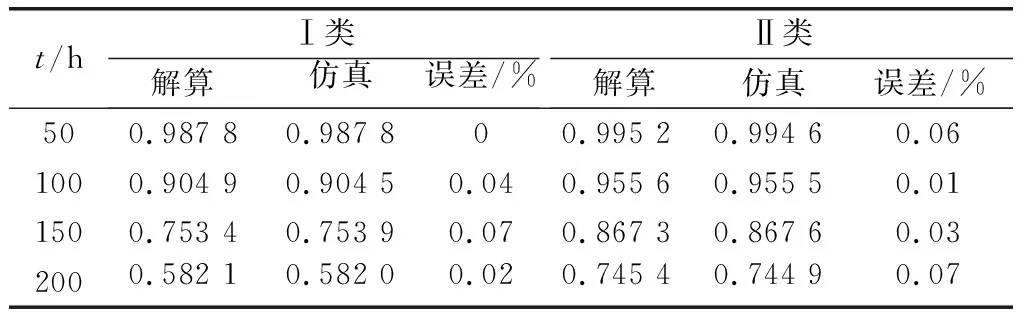
表5 非同型1/3:1(G)系統案例驗證結果

非同型2/3:2(G2)冷備表決系統

系統組件同案例4,工作件服從不同指數分布,當其運行邏輯為2/3:2(G2),仿真與解算結果對比如表6所示。

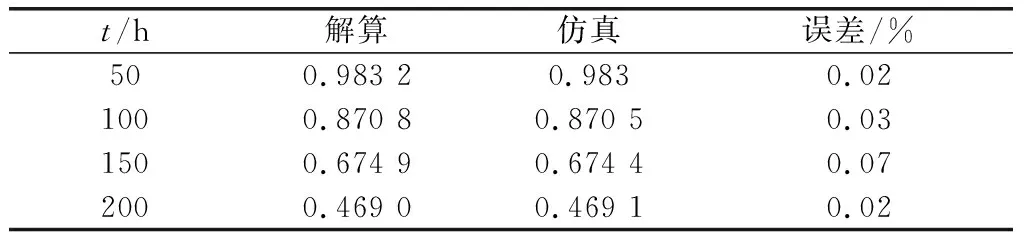
表6 非同型2/3:2(G2)系統案例驗證結果

非同型8/9:1(G)系統

進一步驗證上述方法對部件服從多種分布的復雜非同型k/n:M(G)系統的適用性,考慮部件服從4種分布類型的8/9:1(G)系統,驗證案例的信息如表7所示。取分別為500、700、800、1 000,單位為h,仿真與解算結果對比如表8所示。

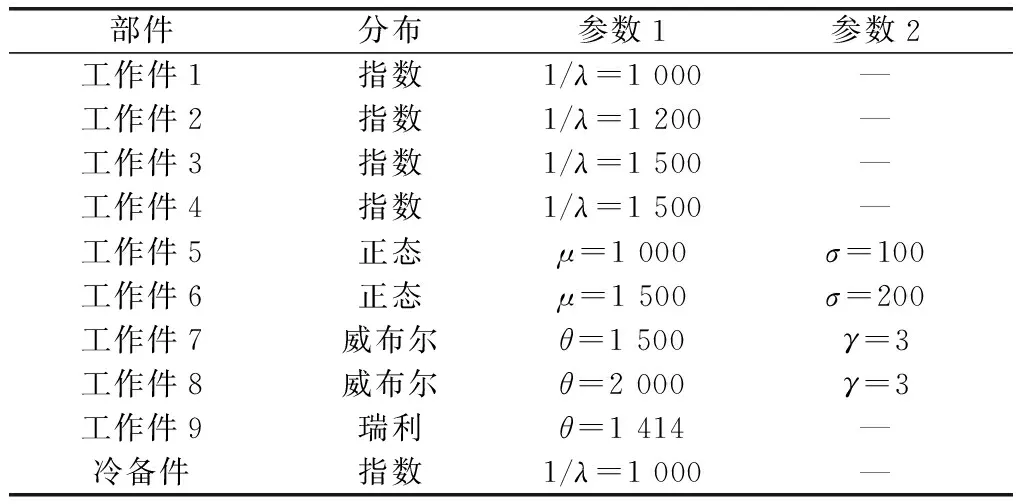
表7 非同型8/9:1(G)系統案例信息

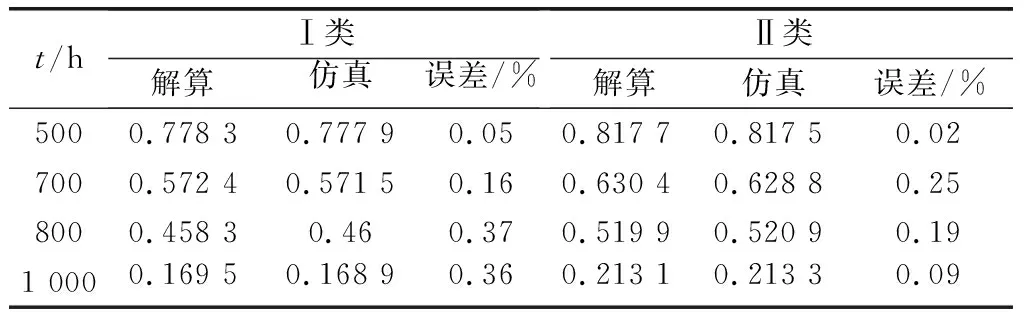
表8 非同型8/9:1(G)系統案例驗證結果

通過以上案例驗證可知,利用蒙特卡羅法獲得的仿真結果與本文方法獲得的解算結果,其相對誤差均不超過1%,利用本文方法可以準確的計算Ⅰ類和Ⅱ類冷備表決系統可靠度。

此外,通過以上案例的Ⅰ類和Ⅱ類冷備表決系統可靠度對比可知,在系統組成結構、部件類型相同的情況下,采用Ⅱ類替換策略,即部件剩余-1個時再進行替換,可以獲得更高的系統可靠性。

6 結 論

本文考慮了k/n:M(G)冷備表決系統的不同運行模式,給出的解算公式可求解系統工作部件和冷儲備件服從任意分布且系統工作部件非同型的系統可靠度。將蒙特卡羅仿真結果與本文求解方法的結果進行對比,結果表明6組實驗誤差均未超過1%,驗證了本文方法的準確性。此外,本文對比了k/n:M(G)系統的不同替換策略,發現采用Ⅱ類策略(即先壞后替),系統具有更高可靠性。

當>1,要求解k/n:M(G)系統可靠度,分析其成功模式,存在著狀態空間爆炸的問題,還需進一步研究簡化的可靠度計算方法。