彈性高超聲速飛行器智能控制系統設計

王 冠, 茹海忠, 張大力, 馬廣程, 夏紅偉,*

(1. 哈爾濱工業大學航天學院, 黑龍江 哈爾濱 150001; 2. 上海衛星工程研究所, 上海 201109)

0 引 言

高超聲速飛行器因其飛行速度快、機動能力強、效費比高等優點,在航空航天及軍事領域具有重要的研究意義。近年來已有不少高超聲速飛行器項目取得長足進步,但由于其具有強非線性、強不確定性、強耦合性等特性,給高超聲速飛行器的控制技術研究帶來了很多問題和挑戰[1]。

當前文獻中,滑模控制[2]、自適應控制[3]、容錯控制[4]等多種先進控制策略已經應用到高超聲速飛行器控制系統設計。文獻[5]針對滑模控制中的抖振現象,設計了高階滑模控制器,實現了高超聲速飛行器的穩定跟蹤控制。文獻[6]將自適應與模糊神經網絡結合,解決了高超聲速飛行器的時變動力學結構問題。文獻[7]在考慮了彈性高超聲速飛行器氣動伺服彈性問題的情況下,構建了一種結合線性自抗擾和自適應陷波器的綜合控制方案,最終達到對頻率時變的彈性振動進行抑制。以上控制技術以及實際工程中廣泛應用的比例積分微分(proportional integral derivative, PID)控制技術可保證一定精度的軌跡和姿態控制。然而,面向未來高超聲速飛行器控制系統的實時、魯棒和高精度需求,現有技術仍存在諸多不足和缺陷。

由執行機構受限導致的輸入受限問題已經成為當前高超聲速飛行器控制領域研究的熱點之一。為了處理執行機構幅值約束,文獻[8]通過引入輔助系統對誤差信號進行補償,保證了高超聲速飛行器在執行機構受限情況下對參考指令的穩定跟蹤。類似地,文獻[9]構建了輔助系統并結合指令濾波器來處理執行機構的幅值和速率約束。文獻[10-11]采用控制分配的方案處理執行機構受限問題,分別基于二次規劃和偽逆矩陣設計了控制器,但存在計算復雜度較高、無法保證分配最優的問題。在此基礎上,文獻[12]提出了一種基于循環神經網絡的控制分配方法,采用該神經網絡近似求解二次規劃問題,然而這一方法對在線計算能力要求較高。模型預測控制(model predictive control, MPC)是當前工業控制界具有代表性且較常用的技術之一[13],能夠很好地解決高超聲速飛行器執行機構的約束問題。文獻[14]設計了一種基于MPC的容錯控制器來處理執行器幅值飽和問題,但是該方法需要飛行狀態量的高階導數,這在實際工程中難以獲得。文獻[15]考慮高超聲速飛行器線性變參數模型下的執行器受限問題,所設計的控制器需要對較復雜的矩陣進行優化處理,由此帶來的緩慢求解速度難以應對實際需求。文獻[16]綜合考慮了控制量的幅值和速率約束,基于神經網絡控制和MPC提出了一種新的控制方法,實現了對氣動舵指令的優化分配。但是,由于MPC的引入大大增加了計算的復雜度,并導致控制系統的指令延遲,這些問題在高機動的高超聲速飛行器控制中尤為突出。

人工智能技術具有精度高、實時表現性強的特點[17],因而其符合未來高超聲速飛行器對控制系統的快速高精度的需求。當前,包括神經網絡控制、深度學習、強化學習在內的智能控制技術逐漸應用于設計航空航天器的控制系統[18-20]。文獻[21]利用神經網絡對未知非線性進行逼近,結合反步法實現高超聲速飛行器縱向動力學控制。文獻[22]基于強化學習技術對衛星控制系統的參數進行調整和更新,實現姿態自適應跟蹤控制。然而,在實際工程和落地轉化中,樣本、算力、最優性以及可靠性等因素制約著人工智能技術的應用。根據S698PM星載計算機的最新數據顯示[23],其600 MHz主頻、20 MB運行內存的星載配置與地面仿真條件存在量級上的巨大差距,很難應用強化學習、深度神經網絡(deep neural network, DNN)等算法。在此情況下,可考慮將這些技術與傳統控制器相結合,即“傳統控制架構+人工智能技術” 來提高控制性能。

基于以上分析,為了實現氣動舵受限下的高超聲速飛行器高精度跟蹤控制,本文提出了一種基于神經自適應的智能控制方案。針對速度子系統,借助強化學習技術對控制器參數的在線調整能力,設計基于深度強化學習(deep reinforcement learning, DRL)的PID參數整定策略,提高控制器的穩定性和魯棒性。在高度子系統中,以神經自適應控制為主體架構,利用非線性MPC (nonlinear MPC, NMPC)對氣動舵指令進行控制分配。不同于已有方法,本文利用NMPC生成大量樣本數據集并訓練DNN,以此代替NMPC進行氣動舵指令優化分配的過程,實現快速計算控制指令,提升系統性能。為了處理外部擾動引入自適應超螺旋微分器,增強了系統的魯棒性。仿真實驗證明所提方案能實現系統狀態的快速穩定收斂,具有較高的跟蹤精度。

1 系統描述和預備知識

1.1 彈性高超聲速飛行器的縱向模型

本文采用的某型高超聲速飛行器的縱向動力學模型[24]為

(1)

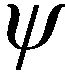
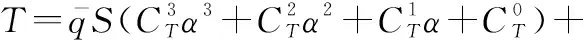
1.2 氣動舵非線性

從工程實際的角度,氣動舵偏角應該滿足幅值和速率的約束:

(2)

式中:δ代表鴨翼偏角δc和升降舵偏角δe。

此外,執行機構動力學模型描述了舵面偏轉或舵機偏轉的動態特性[25],模型描述如下:

(3)

額定狀態下,τSF=0.002 s,ωSF=90 rad/s,ζSF=0.7。

1.3 自適應超螺旋微分器

由于非匹配不確定性等擾動的存在,會給控制器的設計帶來諸多不便,鑒于自適應超螺旋微分器具有良好的逼近效果[26],本文采用自適應超螺旋微分器逼近擾動量以得到更加精確的值。

(4)

(5)

其中,函數h(x)定義為

(6)

其中,c4>0,κ1>0,κ2>0。

根據文獻[26],可知自適應超螺旋微分器的跟蹤誤差是有界的。通過選擇合適的參數,可以保證自適應超螺旋微分器的狀態量在有限時間內實現精確跟蹤。

為便于后面的論證,給出以下引理。

引理 1[27]對于任意的ε>0,下面的不等式成立:

(7)

式中:κ為常數,κ=e-κ-1,即κ=0.278 5。

2 控制器設計

由式(1)知,可以將模型分解為速度子系統和高度子系統。首先針對速度子系統進行控制器設計。

2.1 速度子系統智能PID控制器設計

對于速度子系統,控制器的設計目標是跟蹤速度指令Vr。針對速度子系統,采用PID控制為基本框架。定義速度跟蹤誤差eV=V-Vr,燃料當量比Φ選擇如下的PID控制律:

(8)

式中:kp、ki和kd是PID參數。

PID參數整定是一個復雜的過程,一般需要根據對象慢慢進行。高超聲速飛行器作為一類具有強不確定性和強非線性的被控對象,采用傳統的人工試錯調參方案很大程度上依賴于調試人員的經驗,需要消耗大量的時間,同時難以滿足較高跟蹤精度的需求。針對速度子系統存在干擾等問題,設計一種基于深度強化學習的PID參數整定策略,對于式(8)的PID控制器,根據高超聲速飛行器當前飛行狀態調整PID參數,實現速度指令的跟蹤。

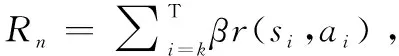
(9)

(10)

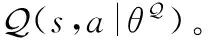
速度子系統作為外環系統,其控制器選用PID便能夠保證良好的跟蹤效果,在許多研究中被采用[8]。本節所設計的基于DRL的PID參數整定策略能夠節約人工調參的時間和成本,保障了高超聲速飛行器速度跟蹤的精確控制。同時,訓練得到的參數整定模塊具有一定的可移植性。對比相對簡單的外環控制器設計,本文采用神經自適應作為主體為高度子系統設計內環控制器。一方面能夠為控制器提供完善的Lyapunov穩定性證明,另一方面能夠在設計過程中解決氣動舵受限下的控制分配問題。值得說明的是,速度子系統中采用的智能PID控制器設計思路同樣可考慮用于高度子系統的控制器設計。

2.2 高度子系統神經自適應控制器設計

2.2.1 RBF神經網絡

本文中通過引入RBF神經網絡來逼近模型不確定項[30]:

f(x)=ωTφ(x)

(11)

式中:f∈R和x∈Rn分別為神經網絡的輸入和輸出;ω∈Rn為權值向量;φ(x)∈Rn為徑向基函數。

f(x)=ω*Tφ(x)+Δ(x)

(12)

(13)

2.2.2 基于DNN的控制分配策略

本節以NMPC為控制指令分配模板,生成大量包含氣動舵指令的樣本數據集,利用DNN學習控制分配策略,實現對氣動舵指令的智能分配。包括樣本數據生成和網絡離線訓練兩個部分。

(1) 樣本數據生成

在當前時刻k,根據期望舵偏角δk生成滿足約束的預測控制序列δp,k。可表示為如下形式的帶約束的非線性規劃問題:

(14)

定義優化目標函數為

J(δp,k)=wLΔL(δp,k)+wMΔM(δp,k)+wδΔδ(δp,k)

(15)

式中:wL>0,wM>0,wδ>0,且

(16)

(17)

(18)

在上述優化問題的目標函數中,Δx=δp,x(k+i|k)-δx(k+i|k),x=c,e表示k時刻對k+i時刻輸出的預測值差；Np和Nc分別表示所采用NMPC方法的控制及預測時域指標。在目標函數中,減小前兩項是為了實現由氣動舵提供的期望升力和力矩,減小第3項是為了平滑控制輸出,且該項的設立可以削弱控制面抖動,保護伺服系統,提高控制面氣動效率。

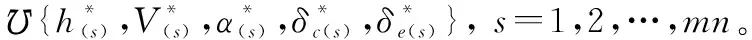
(2) DNN離線訓練

第j層的第i個神經元的輸出如下所示:

fij=G(wijfi-1+bij)

(19)

式中:wij、bij、G分別為第j層第i個神經元對應的權值向量、閾值、激活函數;fi-1為第i-1層神經元的輸出。通過訓練使如下損失函數的值收斂到設定的誤差范圍:

(20)

以上給出了利用DNN學習分配策略的具體步驟,所設計的DNN控制分配模塊將應用在下面設計的控制器中。

2.2.3 神經自適應控制器設計

定義航跡角跟蹤誤差eγ=γ-γr,其導數可表示為

(21)

式中:x1=γ,

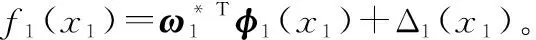
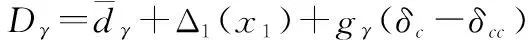
(22)

設計控制律為

(23)

式中:kγ>0,?γ>0。

設計RBF神經網絡的自適應調節律為

(24)

式中:τ1>0,l1>0。通過自適應超螺旋微分器估計Dγ為

(25)

(26)

式中:τγ,1>0,τγ,2>0。

然后,定義期望攻角α*,設計虛擬控制律:

αd=α*-eγ

(27)

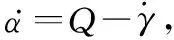
(28)

對此,設計虛擬控制律:

(29)

結合式(28)可得

(30)

定義俯仰角速度跟蹤誤差為eQ=Q-Qd,則其導數可寫為

(31)

式中:x2=[γ,α,Q]T,

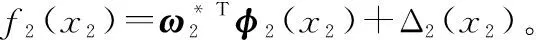
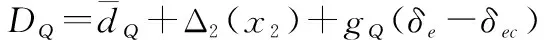
(32)

設計控制律為

(33)

式中:kQ>0,?Q>0。

設計RBF神經網絡的自適應調節律為

(34)

式中:τ2>0,l2>0。通過自適應超螺旋微分器估計DQ,表示為

(35)

(36)

式中:τQ,1>0,τQ,2>0。

以上部分完成了智能控制方案的設計,具體的控制系統框圖如圖1所示。

3 穩定性分析

由于速度子系統采用PID控制器,本小節主要對高度子系統進行穩定性分析。

定理 1針對系統式(1),使用控制律式(23)和式(33),更新律式(24)、式(26)、式(34)和式(36),自適應超螺旋微分器式(25)和式(35),系統可以實現一致有界跟蹤控制,誤差變量eγ、eα和eQ收斂到如下區域:

(37)

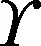
證明選取Lyapunov函數如下:

W=Wγ+Wα+WQ

(38)

式中:

對式(37)求導得

(39)

將式(22)、式(24)、式(26)、式(30)、式(32)、式(34)和式(36)代入式(39),可得

(40)

(41)

其中,

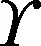
(42)

對式(42)求解可得

(43)

由式(43)可得W(t)≤W(0),即W(t)是有界的,聯合Lyapunov函數式(38),則有

(44)

進一步可得

(45)

式中：x=γ,α,Q。

證畢

4 訓練設計和仿真結果

4.1 速度子系統強化學習訓練

在設置基于DDPG算法的離線訓練時,設計最大的訓練回合為3 000,每回合最大步長為500,采樣時間為1 s。為使DDPG智能體適應多種環境,需要將訓練期間的參考軌跡設計在表1所示的飛行包線內,且盡量覆蓋不同類型具有代表性的飛行任務。

表1 高超聲速飛行器的狀態約束

由于高超聲速飛行器的狀態值不在同一個數量級,訓練所需的狀態值需進行歸一化處理為有效數據,然后隨機采樣進行訓練。當飛行任務輸出完成時,該回合停止,同時計算當前回合的總回報獎勵。表2給出了具體的訓練參數設置。

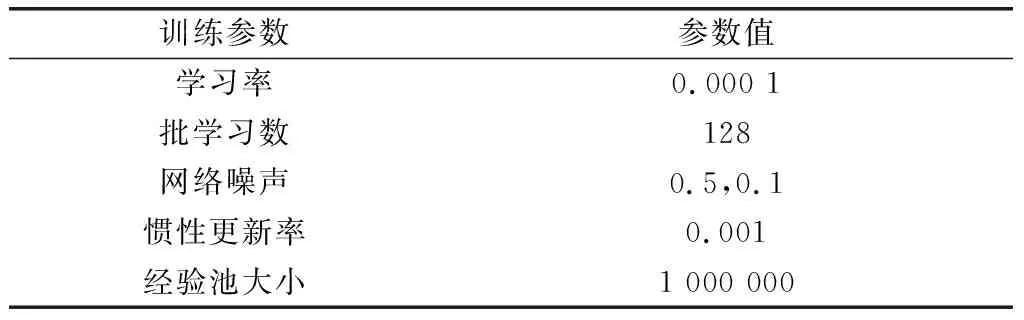
表2 訓練參數設置

由圖2可以看出,累計回報曲線在400回合附近逐漸呈現收斂趨勢。最后,訓練好的DDPG智能體將被移植于速度子系統控制器中,用于自適應調整PID參數。

4.2 高度子系統神經網絡訓練

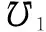
4.3 仿真結果

為了驗證所提出方案的有效性,本文設計如下兩個仿真實驗。其中,模型中的氣動數據見文獻[21],速度和高度參考信號采用文獻[16] 給出的指令濾波器,高超聲速飛行器的狀態初值如表3所示。

表3 高超聲速飛行器的狀態初值

本文的設計參數分別為kh=kγ=0.1,kα=1,kQ=5,其余參數根據具體仿真實驗和式(42)的約束進行適當調整。

4.3.1 驗證仿真

為驗證所提出控制方案的有效性,設計如下由階躍信號產生的參考指令:

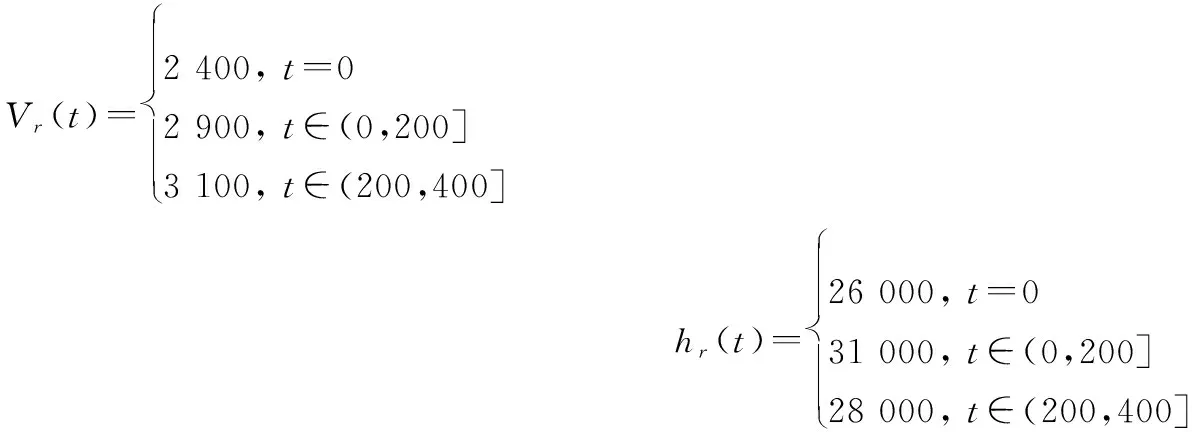
為了驗證控制器的魯棒性,引入以下干擾:當120≤t≤140,dV=2 cost;當220≤t≤240,dγ=0.005 cost;當320≤t≤340,dQ=0.02 cost,時間t的單位為s。

仿真結果如圖4～圖6所示。圖4給出了速度和高度的跟蹤結果,可以看出系統在干擾作用下的速度和高度都能夠穩定跟蹤設定的參考軌跡。圖5顯示的是系統狀態響應曲線,包括航跡角、攻角、俯仰角速率以及彈性模態,可以看出航跡角和攻角具有比較小的跟蹤誤差。圖6給出了包括燃料當量比、鴨翼偏角和升降舵偏角在內的輸入變化曲線,本文所考慮的氣動舵受限問題得到了有效解決。圖7給出了PID的變化曲線,可以看出kp、ki、kd隨著系統狀態變化,最終趨于穩定。神經自適應控制的權重變化在圖8中體現。圖9和圖10給出利用自適應超螺旋微分器處理擾動和誤差上界的估計值。此外,為了研究基于NMPC和DNN優化分配控制器的性能對比,表4給出了基于同一平臺(CPU: i7-7700HQ,RAM: 16.0 GB)的仿真時間。可以看出,基于DNN優化分配的方案將計算速度提升近90%。這主要是因為NMPC需要解決執行器模型的優化問題,而利用DNN代替復雜優化問題的過程將明顯縮短計算時間。

表4 控制分配算法運行時間比較

4.3.2 對比仿真

為了進一步驗證本文方法的優越性,選取文獻[16]中的神經自適應控制器(簡稱對比方法1)以及文獻[3]中的自適應反步控制器(簡稱對比方法2)與本文所提出的控制器(簡稱本文方法)進行對比。速度參考指令跟蹤幅值為200 m/s的階躍信號,高度指令為幅值為10 000 m的階躍信號。圖11～圖14為對比仿真的實驗結果。

從圖11可以看出,以上3種方法均能夠實現良好的跟蹤控制性能。通過對比可以發現,本文所提出的控制方法具有較快的跟蹤性能和較好的跟蹤效果,主要是因為所采用的智能控制方法實時調整控制參數以及網絡權值,并且采用的自適應超螺旋微分器對控制器提供較好的補償。圖12和圖13分別給出了對應的系統狀態曲線和控制輸入曲線,其中包括鴨翼偏轉角和升降舵偏轉角根據目標函數進行了優化分配的控制輸入曲線。圖14給出了3種方法在500次蒙特卡羅仿真下的平均絕對誤差曲線對比,可以看出,本文方法具有更高的跟蹤精度。

5 結 論

針對彈性高超聲速飛行器氣動舵受限情況下的高精度跟蹤控制問題,設計了一種基于神經自適應的智能控制方案。應用DRL方法構建了智能參數整定策略,實現了對速度指令的快速跟蹤控制。考慮氣動舵的約束和動態特性,設計了基于DNN的智能分配策略,并給出了神經自適應控制器設計過程和穩定性證明。通過引入自適應超螺旋微分器處理外部擾動,有效地增強了智能控制系統的魯棒性和抗擾能力。仿真結果表明,所提出的方案能夠較好地處理氣動舵受限問題,并實現快速高精度的速度和高度跟蹤控制。