雙正弦波紋柔性鉸鏈的設計與分析

伍建軍，王振飛

（江西理工大學 機電學院，贛州 341000）

0 引言

柔順鉸鏈相對于傳統依靠固定鉸鏈的多桿傳動機構，結構更加簡化，其通過構件的變形而產生力和位移[1]。目前精密定位技術廣泛應用于微型機器人、生物科學研究以及工業生產等領域[2]。使用柔順機構精密定位具有免裝配、無摩擦等優點，避免了由于鉸鏈間隙造成的誤差[2]。基于柔順機構的定位平臺的工作空間受限于鉸鏈的彈性形變范圍，而傳統矩形截面鉸鏈和圓形截面鉸鏈主要受剪切力形變，在遇到壓拉力形變時，行程十分有限。田延嶺等[3]設計出一種由彈性鉸鏈作為其導向機構的串聯微定位平臺；崔玉國等[4]基于Stewart并聯機構，研制出具有對稱雙圓弧薄板式彈性單元體的微動平臺新構型；王念峰等人[5]設計了一種以半圓形波紋簧片的兩自由度精密定位平臺，著重進行了鉸鏈的分析與有限元的對比，具有良好的解耦性。

綜上所示，本文以實現輸出位移大、結構緊湊的目標，提出了一種雙正弦波紋的柔性鉸鏈，在平面位移的兩自由度上都具有良好的傳導性，以此來替代傳統剛性運動副進行力和位移的傳導。分析傳統鉸鏈相比于波形鉸鏈的不足之處，使用ANSYS將之進行單段和多段的對比分析驗證雙正弦波紋鉸鏈的優勢。

1 正弦波紋鉸鏈設計

根據伯努利梁理論，對于一般懸臂梁的最大撓度可以用式(1)表示：

式中，δ為懸臂梁末端的撓度；F為施加在懸臂梁末端上的力；L為懸臂梁的長度；E為懸臂梁的彈性模量；I為轉動慣量。其中，轉動慣量I與懸臂梁的寬度b和厚度h有關，如式(2)所示：

因此，在材料和載荷不變的情況下，改變懸臂梁的長度以及寬和厚度便可以改變懸臂梁的最大撓度。假設懸臂梁的寬度與厚度不變，只改變其長度，可以將一般的懸臂梁設計為如圖1所示的三角形和矩形周期性懸臂梁的形式[6，7]。然而，雖然增加了梁的長度，但由于在拐角處出現的尖銳角，極易產生應力集中的問題。

圖1 三角形和矩形周期性懸臂梁

綜上所述，又根據王念峰等人提出的半圓形波紋柔性鉸鏈，如圖2所示。考慮到其結構緊湊在y軸方向上的行程有所不足，若適當增加每半個波紋之間的距離，便可以有效改善這一現象。基于此設想一，本文提出了一種基于正弦的曲線波紋鉸鏈，其公式如式(3)所示。

圖2 半圓形波紋柔性鉸鏈

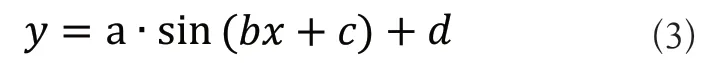
為對比兩者的行程，將在下一節中采用有限元仿真對其進行靜力分析，通過對比其x軸與y軸方向的最大位移來驗證其性能。

2 有限元對比分析

為了便于傳統矩形截面鉸鏈和圓形截面鉸鏈、半圓形波紋鉸鏈以及正弦波紋鉸鏈的對比，使其柔性部分總長、最薄弱處厚度、材料以及外力都統一。各鉸鏈的柔性部分使用鋁合金材料Al7075-T651。其中，半圓形波紋鉸鏈的厚度t=0.1mm，w=10mm，R=1mm，正弦波紋則采用等距0.1mm來繪制，各參數取值分別為a=2，b=1，c=0，d=0，在ANSYS中將其進行靜力學分析，如圖3所示。

圖3 各鉸鏈x軸向位移云圖

經有限元分析驗證，在各外部條件都一致時，半圓形波紋柔性鉸鏈的最大位移確實要好于傳統鉸鏈，但正弦波紋柔性鉸鏈的行程更為可觀，是半圓形波紋柔性鉸鏈的2.18倍。由此可見，波紋形鉸鏈在行程方面相比于傳統矩形截面以及圓形截面的鉸鏈有很大的優勢，同時波紋鉸鏈的行程隨著波紋單元的增加，其最大行程也會不斷增加。本文所提出的正弦波紋鉸鏈的性能相比于半圓形不僅在x軸向上的位移更佳，而且在y軸方向變形量也同樣更具優勢，如圖4所示，是半圓形的2倍，驗證了設想一的合理性，正弦波紋鉸鏈的柔度相比較于半圓形波紋更大。

圖4 波紋柔性鉸鏈y軸方向位移云圖

2.1 雙正弦波紋鉸鏈設計分析

雖然相比與圖1所示的三角形和矩形周期性懸臂梁拐角的容易產生應力集中的尖銳角，波紋柔性鉸鏈已經有所改善，但是在交變載荷的作用下，等厚波紋鉸鏈在波峰波谷處仍舊容易產生應力集中的現象，而導致疲勞勞損問題。據此，提出設想二：若在保持單元波紋整體側面面積不變的情況下，將其尺寸進行合理分布，在波峰波谷處適當增加厚度，可以有效改善應力集中的現象。而將正弦曲線上移0.1mm后所形成的雙正弦波紋鉸鏈則剛好可以達到相應的效果，單元等距正弦波紋和雙正弦波紋的側界面曲線圖分別如圖5所示。

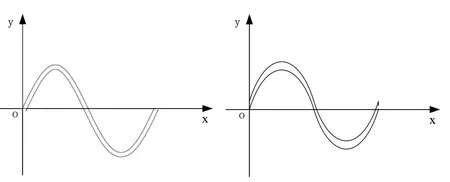
圖5 等距正弦與雙正弦單元波紋曲線圖

由圖5可以看出，等距0.1mm和上移0.1mm的正弦曲線所形成的波紋鉸鏈外形有所差異，雙正弦波紋鉸鏈的厚度在波紋方向是不斷變化的。如圖6所示，采用作圖法[8]，選取雙正弦單元波紋曲線作為作圖對象，作y1的切線l1與y1相交于點A(x1，y1)，再作l1的垂線l2交y2于點B(x2，y2)，連接OA和OB，OA與x軸夾角為α，OB與x夾角為β。如式(4)所示，根據投影定理，將三條線段投影于x軸，并采用向量法來表示其厚度的變化情況，通過式(4)、式(5)可以得出厚度AB的變化公式，如式(6)所示。

圖6 厚度AB作圖示意圖

將點A(x1，y1)和點B(x2，y2)坐標代入式(6)，可以得出|AB|的表達式(7)，再聯立y1和y2的正弦曲線公式以及式(7)使用MATLAB計算，結合各參數取值范圍如式(8)所示，便可以得出雙正弦波紋鉸鏈的厚度|AB|的變化曲線圖，如圖7所示，可以看出，厚度在波峰波谷的時候厚度值達到最高值，并以此建立對應的雙正弦波紋鉸鏈模型，對其進行有限元分析驗證，是否可以有效減少應力集中的問題。

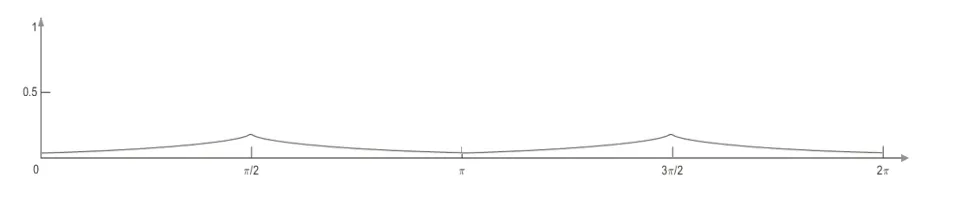
圖7 厚度AB變化曲線圖

2.2 波紋鉸鏈靜力學分析對比驗證

在三維軟件進行數字建模后，使用ANSYS對這三種波紋鉸鏈進行靜力學分析，得出三者在x軸和y軸上的最大行程以及最大應力，仿真結果如表1所示。由表中數據可以看出，等距正弦鉸鏈在x軸和y軸方向的最大位移，都是半圓形鉸鏈的2倍，最大應力則分別是3.4倍和1.5倍。但是在考慮到波紋鉸鏈波峰和波谷的在交變載荷作用下帶來應力集中的問題，而采用雙正弦鉸鏈使得波紋鉸鏈厚度尺寸得到更合理的分布后，由數據可以直觀地看出其優勢。雙正弦波紋鉸鏈在x軸和y軸方向上的最大位移分別是半圓形的14.8倍和8.9倍，最大應力甚至增加到了15.6倍和3.1倍。通過數據可以清楚地看出，相比于等厚的半圓形和等距正弦鉸鏈，在相同外部作用載荷下，以及同樣的材料和空間內，采用雙正弦結構的鉸鏈在性能上更具優勢，無論是在x軸和y軸的行程上，還是在能承受的最大應力方面，都得到了顯著的提高。同時，也驗證了先前2.1節中所提出設想二的正確性，合理的尺寸分布確實可以有效提高波紋鉸鏈的性能。

表1 三種波紋鉸鏈有限元分析數據對比表

（續）

2.3 雙波紋對稱結構分析

鉸鏈在外部載荷產生的最大位移是衡量柔性鉸鏈平臺的一個重要指標。為進一步驗證先前理論的合理性以及實用性，參考王等人將波紋鉸鏈應用于定位平臺的方案，本文中選取各波紋的雙波紋對稱結構來作為試驗對象，通過靜力學和模態分析對其性能進行對比參照，來分析三者的優劣。通過模擬在相同的作用力下，各波紋結構在x軸和y軸方向上的位移和應力應變情況，半圓形波紋、等距正弦波紋、雙正弦波紋鉸鏈的靜力學仿真結果依次如圖8和圖9所示。

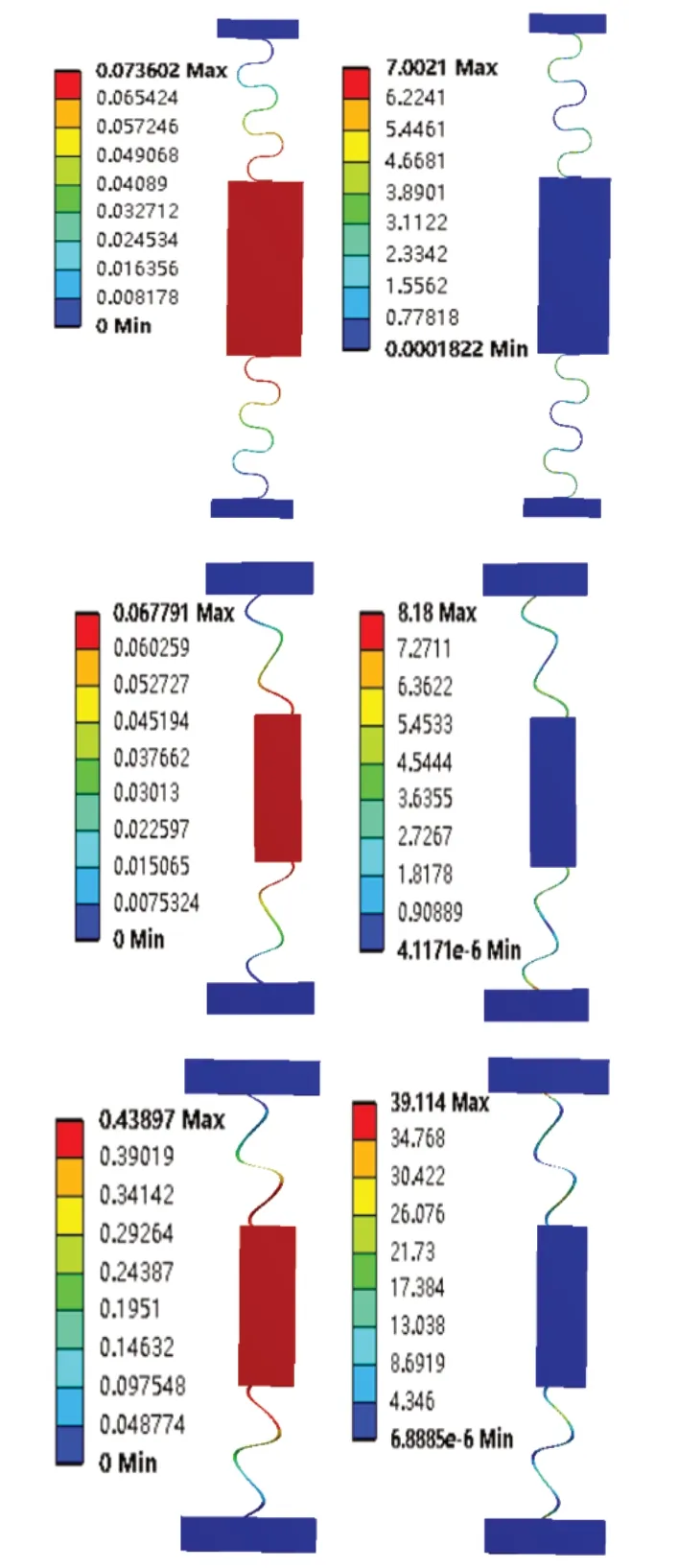
圖8 x軸方向受力位移及應變云圖

圖9 y軸方向受力位移及應變云圖

根據靜力學仿真結果，可以看出在將波紋鉸鏈應用于類似定位平臺的環境時，等厚度的半圓形與等距正弦波紋鉸鏈在x軸方向上的位移和應力都相差不大，而在波峰波谷厚度有所變化的雙正弦波紋鉸鏈的行程和最大應力都要較大程度上高于等厚波紋鉸鏈，說明合理的尺寸分布，不僅可以改善交變載荷下造成的應力集中現象，同樣也可以有效提升波紋鉸鏈在定位平臺上的應用性能。相應的，在y軸方向上則可以清楚看出，正弦波紋鉸鏈的最大位移和應力都要高于結構相對緊湊的半圓形波紋鉸鏈，同時也驗證了1節中所提到的設想一。由此可見，雙正弦波紋在x軸和y軸上的行程和最大應力相比于半圓形波紋鉸鏈皆得到了很大的提升，說明若將其應用于定位平臺同樣也可以使得定位平臺的性能得到一定的提升。

考慮到由于正弦波紋鉸鏈柔度高于半圓形波紋鉸鏈，可能導致正弦鉸鏈會比半圓形鉸鏈更易受外部振動影響，而帶來共振問題導致結構破壞的情況。因此，需要對三者進行相應的模態分析，觀察其各階模態下對應的頻率變化情況，具體參數如表2所示。

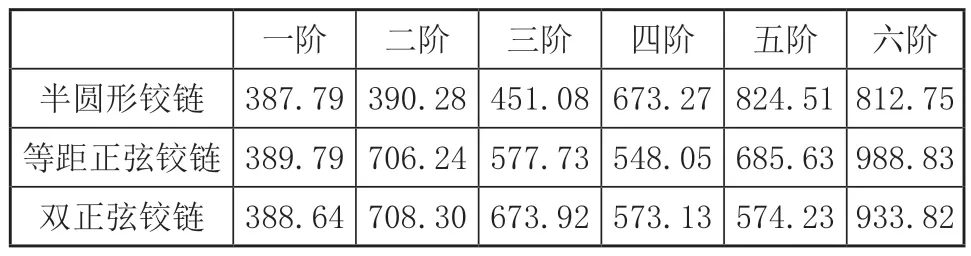
表2 三種波紋鉸鏈各階模態固有頻率（Hz）

模態是結構系統的動力學特性，是系統的固有振動特性，每一階模態都對應一個特定的固有頻率[9]。對三種波紋鉸鏈進行模態分析，可以了解到它們的固有頻率范圍，可以針對性地避免產生共振而導致損壞。由表2中的數據可以看出，這三種波紋鉸鏈的六階固有頻率范圍都相差不大，皆在Hz380～1000Hz之間。對此，也在一定程度上說明，這三類波紋鉸鏈可以用于相類似的工作環境之中。在柔順鉸鏈的質量(m)和材料為定值時，剛度越小則柔度越大，固有頻率也越大。其中，剛度(K)與柔度(δ)以及剛度與固有頻率(f)的關系式分別如式(9)和式(10)所示。

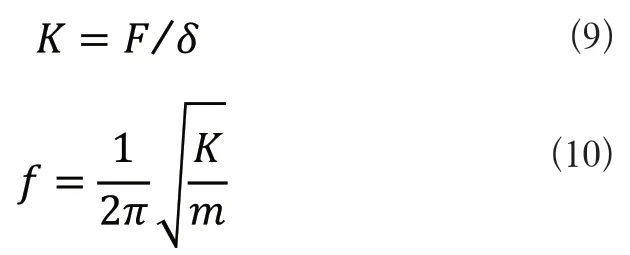
由式(9)和式(10)可看出剛度與柔度成反比關系，固有頻率則與剛度也成反比關系。通過聯立式(9)和式(10)可以得到固有頻率和柔度的關系式，如式(11)所示。

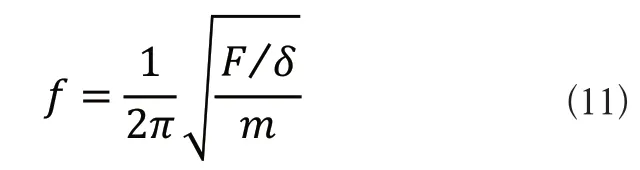
本文中為得到行程更佳的鉸鏈，根據式(11)所示，當固有頻率越大則柔度更大，同時，所得鉸鏈的行程也更佳。以平面二自由度定位平臺的位移為例，由于一階和三階模態分別是在x軸和y軸方向的振波頻率，以兩者為主要判別依據對雙波紋對稱結構進行對比分析。從表2數據可以看出，在x軸向上，波紋鉸鏈固有頻率大小差距不大，正弦波紋鉸鏈略微大于半圓形鉸鏈，說明x軸方向上正弦鉸鏈的柔度只是略優于半圓形鉸鏈。而在y軸方向上正弦鉸鏈固有頻率數值明顯要要高于半圓形鉸鏈，且雙正弦鉸鏈的數值更佳。綜合分析可知，根據式(11)中波紋鉸鏈固有頻率和柔度的關系式，結合各階模態分析的數值可以看出，數值與靜力學仿真結果大體一致，說明作為雙波紋對稱結構應用于定位平臺時，雙正弦波紋鉸鏈也同樣具有一定優勢。

3 對比驗證

為了更直觀地將單波紋和雙波紋鉸鏈結構的有限元分析結果進行對比驗證，其最大位移、最大應力以及相應的提升率如表3所示。

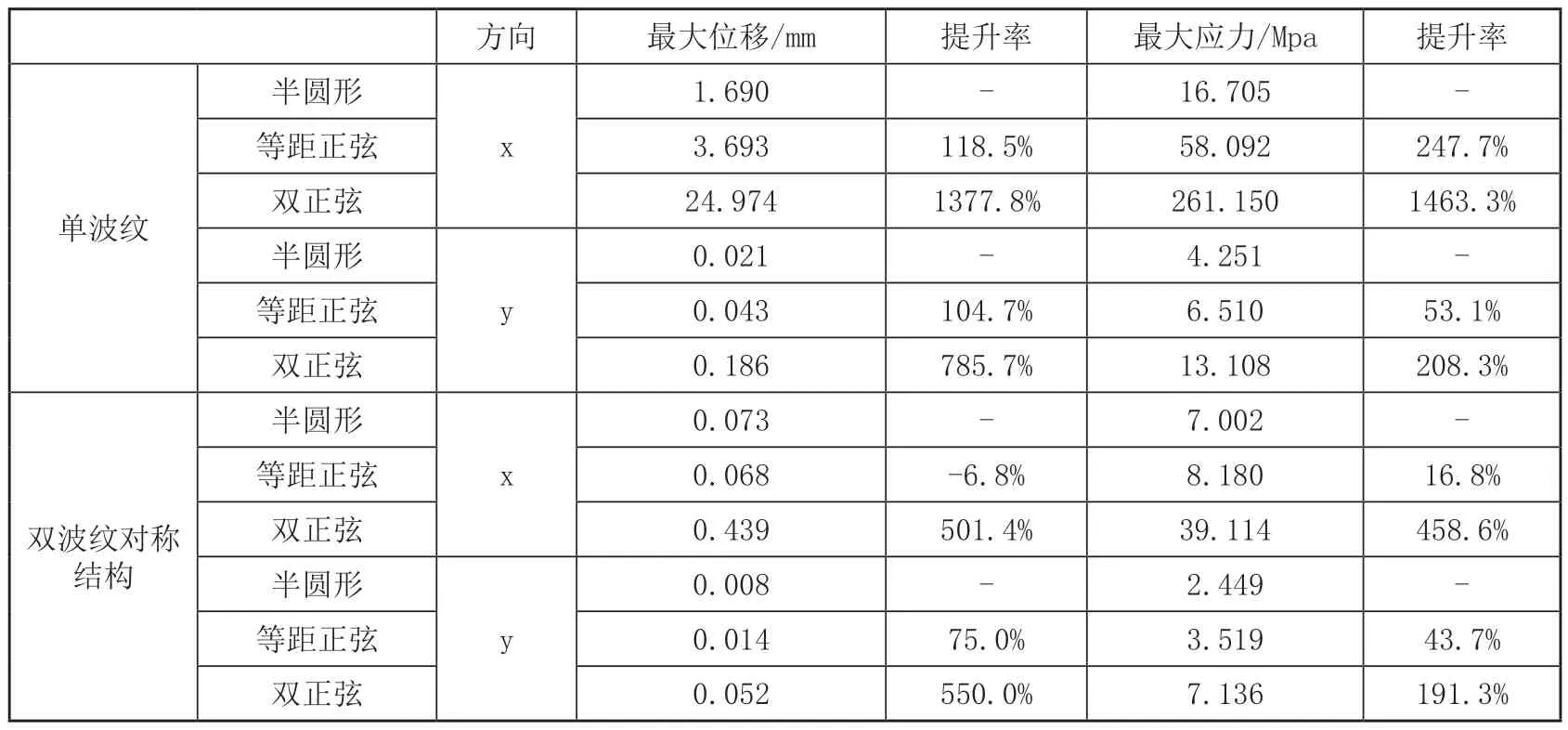
表3 波紋鉸鏈靜力學分析結果對比表

從表3中的數據可以看出，對于等距正弦波紋鉸鏈，在單段的結構時，最大位移以及應力方面相比去半圓形鉸鏈提升皆較為顯著，而在應用于雙波紋對稱結構時，可以看出，其在x軸的位移提升效果并不理想，但可以證明正弦鉸鏈相比于半圓形鉸鏈，在y軸位移具有一定的優勢，同時也驗證了1節中所提出的適當增加每半個單元波紋的距離設想一的正確性。針對于在交變載荷作用下，避免等厚鉸鏈波峰波谷出現應力集中的問題，將其厚度進行合理分布后得到的雙正弦鉸鏈，則明顯改善了等距正弦波紋鉸鏈的不足之處，無論是在x軸和y軸的位移方面還是在最大應力方面，性能都得到了巨大的提升，有效證實了2.1節中所提出設想二的正確性。

4 結語

1）提出了一種基于雙正弦曲線的波紋鉸鏈設計，根據投影定理采用向量法計算出波紋鉸鏈厚度的變化情況，通過實例仿真分析驗證了正弦波紋鉸鏈理論分析的正確性。

2）將半圓形、等距正弦波紋鉸鏈與雙正弦波紋鉸鏈的單段波紋，以及根據定位平臺而設計的雙波紋對稱結構，進行性能對比。結果表明，在y軸行程上，正弦波紋鉸鏈明顯優于半圓形鉸鏈；在x軸行程上，雙正弦波紋鉸鏈有效改善了波峰波谷會出現的應力集中問題，進行合理尺寸分布后的性能顯著提高。這也充分表明了雙正弦波紋鉸鏈結構設計的合理性與有效性。

3）由于本文中的同尺寸雙正弦鉸鏈參數受到人為設定的影響，若對曲線的參數a、b、c、d進行優化設計，所得的波紋鉸鏈效果會更加。同時也可以嘗試不同尺寸的正弦曲線組合來進行優化設計，為波紋鉸鏈設計提供了一定的研究思路。