岸邊集裝箱起重機防風系固裝置松弛設計

孫亞平 曾 鵬 羅振國 王寶海

上海振華重工(集團)股份有限公司 上海 200125

0 引言

防風系固是岸邊集裝箱起重機（以下簡稱岸橋）的重要安全裝置，其在暴風時，起限制起重機輪子抬起和防傾覆的作用。隨著國際集裝箱船舶大型化，岸橋的參數越來越大，抗暴風要求也越來越高，故對碼頭的系固承載能力要求也越來越高。對于新碼頭，在建造時需投入更大的成本；對于老碼頭，系固承載能力的限制制約了設備的升級換代。因此，更加科學、準確地對防風系固裝置進行設計計算，變得越來越迫切。

本文運用結構有限元FEA，計算分析輪壓、系固和松弛的關系，指出了傳統認識的不足，進而介紹了松弛設計原理，證明其能顯著降低系固力。在此基礎上，運用反力互等、局部剛度、自重撓度關系，從輪壓出發，給出了一種實用的簡化計算方法。

1 存在的問題

傳統上認為系固裝置必須是收緊的才能起到系固作用，實際上存在誤區。例如某岸橋大梁80°抗暴風，載荷組合為DL+TL+LS+1.2WLS，其中DL為固定質量，TL為小車質量，LS為吊具質量，WLS為暴風載荷。各風向如圖1所示，風向W4為陸側角度風，W5為海側角度風，W1為大車方向平行風。A、B、C、D表示4條門腿位置，以腿壓表示位置大車行走機構所有輪壓之和。文中傾覆力矩滿足W1＞W5=W4。

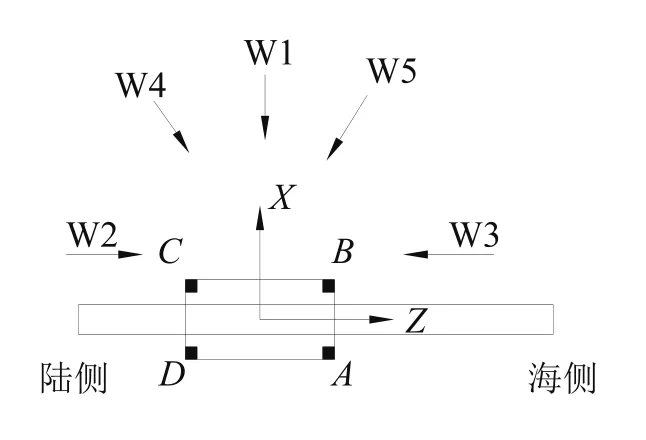
圖1 風向、位置示意

如圖2所示，定義杠桿比

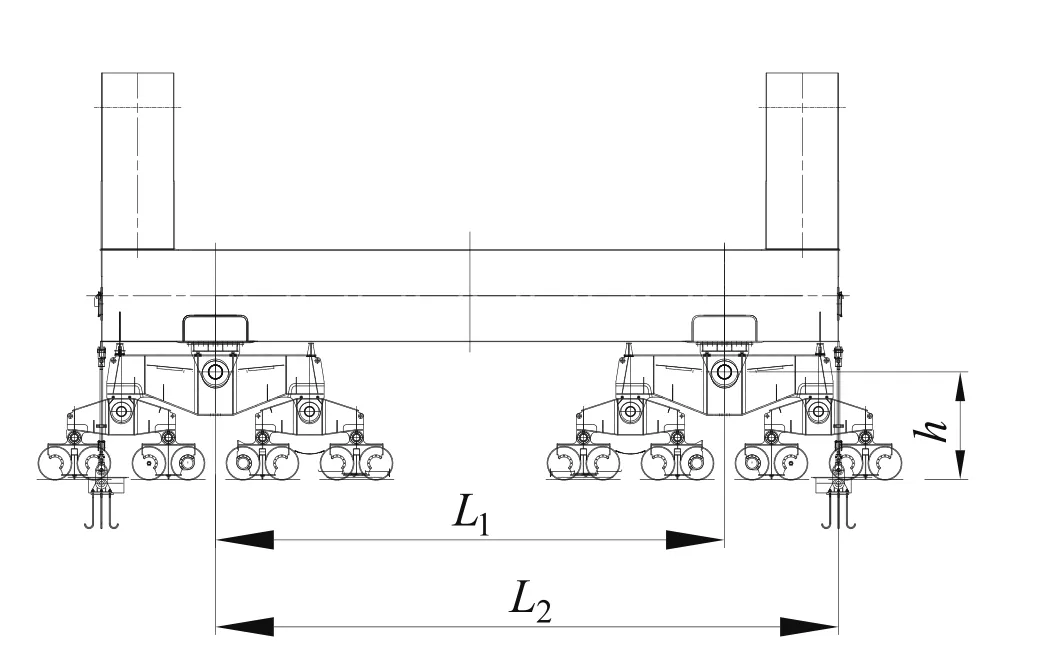
圖2 大車系固位置圖

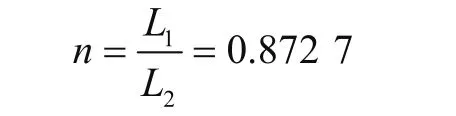
式中：L1為大車基距，L1=15.7 m；L2為系固離另一側大車距離，L2=17.99 m。通常系固裝置位于橋吊大車行走機構外側，即L2＞L1。

以下采用FEA來進行防風系固的研究，計算時遵循：

1）車輪只能受壓（正值），系固只能受拉（負值）。

2）自重時，系固收緊，且剛好不受力。具體FEA計算中采用link單元，通過設置單元預應變來進行控制。輪壓、系固力結果如表1。

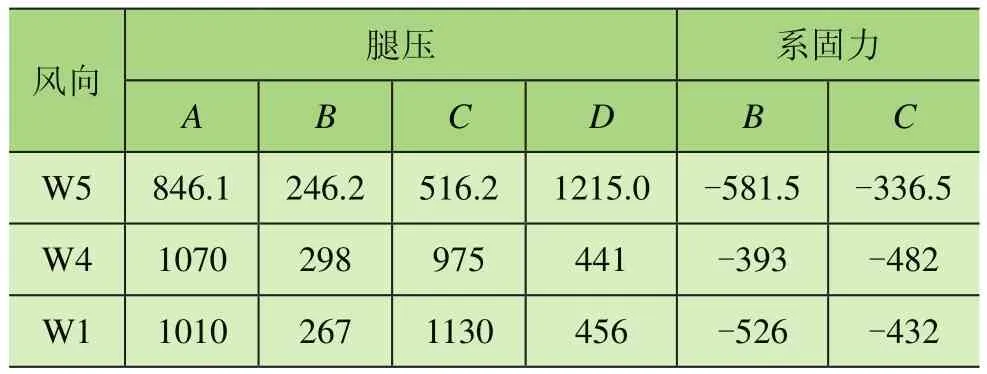
表1 FEA腿壓、系固力 t

因為系固裝置僅在出現負輪壓時才需要，由表1可見，W5、W4、W1時均有顯著的正輪壓，這與防風系固的設計原則有所矛盾，進一步從受力上看，系固與輪壓是一對內力，它們互為反作用，且正輪壓對系固載荷起了增大作用。可見，系固收緊會導致輪壓和系固載荷同時增大，適當松弛反而可以釋放正輪壓和系固載荷。

2 松弛設計原理

系固通常位于大車外側且靠近立柱，如圖3所示。自重條件下的垂直變形如圖3a。當系固收緊且有側向風載荷時，由于起重機鋼結構不是完全剛性的，防風系固優先、直接承受上拔力。而下部結構的下橫梁、大車行走結構重量此時無法參與受力。可以設想，將B處系固適當松弛，B處會逐漸產生抬腿；直至B處輪壓為0(即消除正輪壓)，如圖3b所示。此時，下橫梁和大車質量起到了抵消上拔力的作用，從而降低了系固載荷。

隨著松弛增加，直至C處也開始抬腿，如圖3c所示。此時，由于C處的輪壓也參與抵消了上拔力，從而進一步降低了B處的系固載荷。

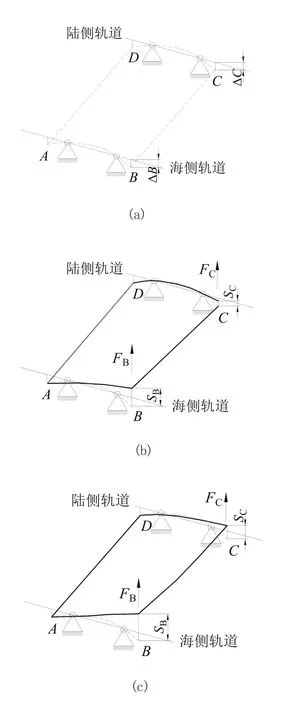
圖3 抬腿示意圖

因此，引入系固松弛與大車抬腿的理念，合理設計系固松弛量并允許門腿適量抬起，可以充分依靠正輪壓來克服上拔力，從而達到降低系固載荷的目的。

系固松弛定義為當自重作用時系固剛好收緊，以此為初始狀態，當此基礎上的松弛即松弛量。采用結構有限元計算FEA時，考慮僅海側或海陸側都有防風系固2種情況。通常情況下，海側角度風時有最大系固載荷，故以下按W5、W4、W1順序做計算研究。

3 計算研究

3.1 僅海側有系固時

從海側角度風(表2中序號1)出發，增加系固松弛量使得海側抬腿直至B處輪壓剛好為0(表2中序號2)，此時陸側C還有正輪壓，繼續增大B處系固松弛并直至C處輪壓為0(表2中序號3)，此時能得到海側最小系固載荷。在W4，W5風向時的系固載荷如表2中序號4、5。表中抬腿是指大車處抬起。

由表2可知：1）海側角度風時系固適當松弛，系固力從601.1 t低至374.0 t，下降了37.8%。這是由于大車剛度較大，系固松弛后，系固載荷下降較快。2）當松弛至陸側輪壓為0時，從374.0 t進一步降到252.6 t，為單側抬腿時的67.5%。此時由于抬2條腿，系固載荷最小，即為252.6 t。此時系固載荷僅與風載傾覆力矩有關。W4與W5的系固力相等，是因為風載傾覆力矩相等。

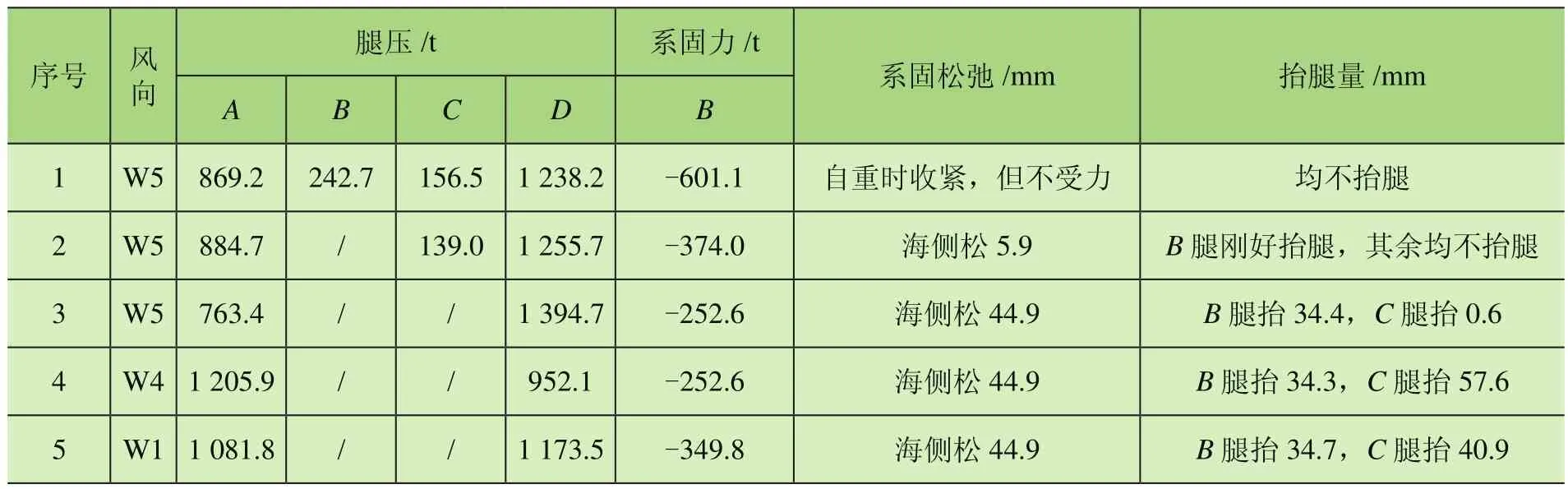
表2 僅海側有系固時的腿壓、系固力、松弛、抬腿結果

3.2 海、陸側均有系固時

同單側系固時類似，計算結果如表3。由序號3，4可知，只要B、C抬腿時，對應海、陸側系固力之和相同，也就是只與傾覆力矩有關。

由表3可知：1）當設海、陸側系固時，海側角度風時系固適當松弛，最大系固力從581.5 t低至374.3 t，下降了35.6%。同樣是因為大車剛度較大，所以系固松弛后，系固載荷下降較快。2）調節海、陸側松弛量，可調節海、陸側系固力，對于海陸側系固許用值不同的碼頭，這一可調特性，給系固設計帶來了一定的靈活性，特殊情況下能使兩側相等。另外，系固還起到了調節腿壓的作用。

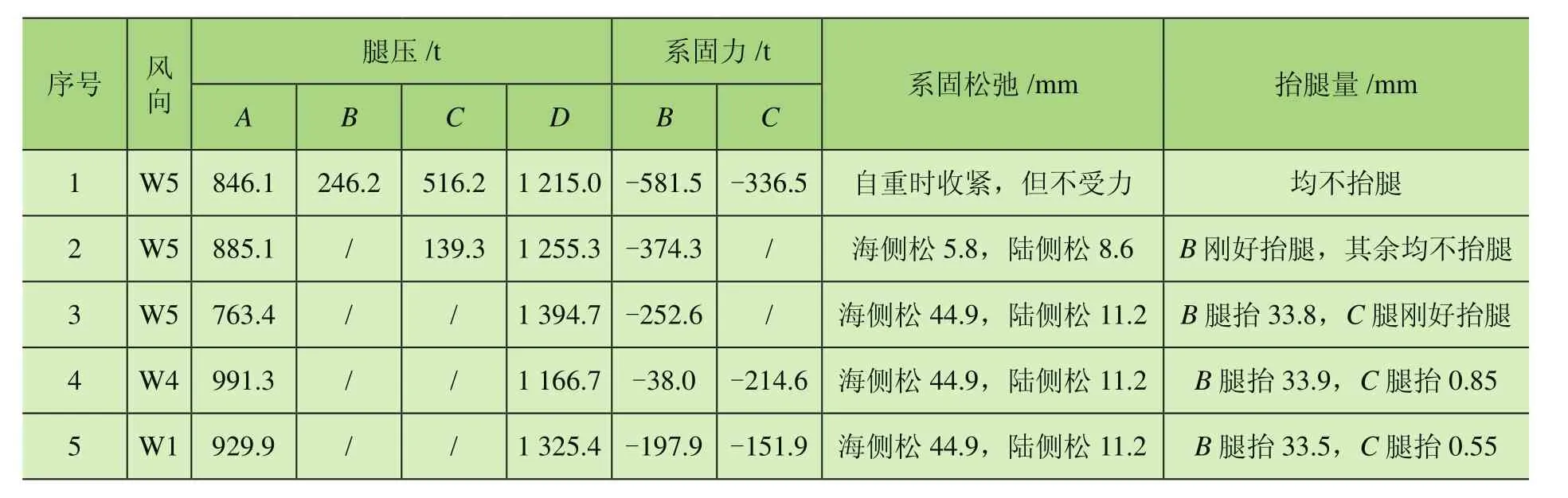
表3 海、陸側均有系固時的腿壓、系固力、松弛、抬腿結果

4 簡化算法

4.1 輪壓關系

本文岸橋大梁80°時自重輪壓、暴風FEA輪壓結果如表4所示。

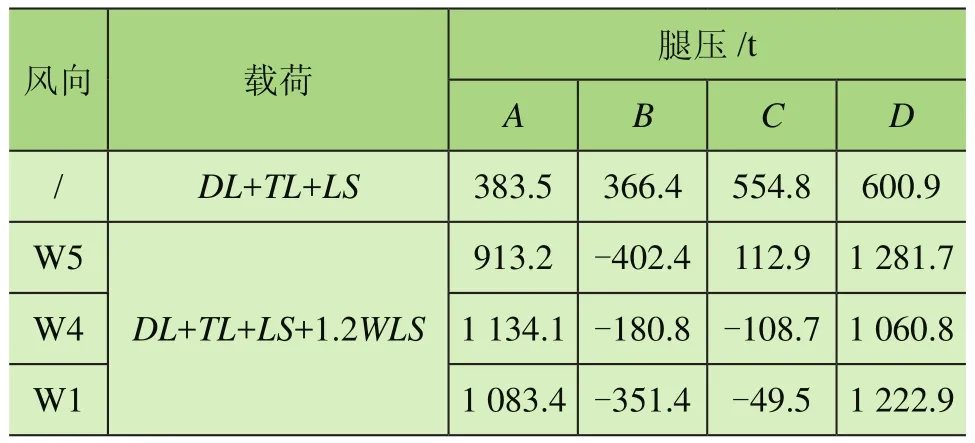
表4 FEA腿壓

4.2 剛度關系

結構剛度定義為對于整機結構，當大車A、C、D位置約束，在B處大車軌道面作用垂直載荷F時，產生垂直變形ΔL，結構剛度為

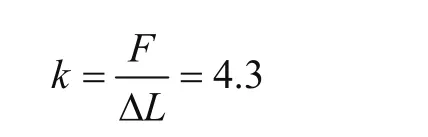
根據反力互等，A、C位置大車產生的支反力-F，D處大車反力F；B處系固的垂直變形近似為ΔL/n。式中：n是文前定義的杠桿比。

根據有限元結果，僅自重時，B、C系固位置下撓ΔB=6.5 mm，ΔC=10.2 mm，如圖3a所示。當輪壓從有輪壓減為0時，系固位置的自重變形近似為0。

4.3 簡化算法

B、C處總輪壓：自重時設為B0、C0；W5風向時設為B1、C1；W4風向時設為B2、C2。

B、C處系固位置：系固力為FB、FC，自重時下撓ΔB、ΔC。

1)海測系固

根據W5的輪壓，為使海側系固力最小，即充分利用C處正輪壓，得系固力

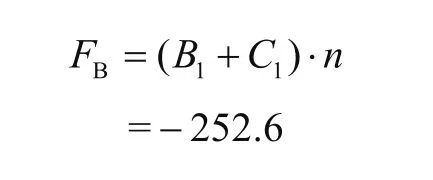
設B、C處松弛為SB、SC，得

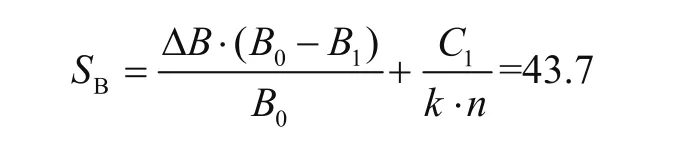
與表3中序號3的松弛44.9 mm相比僅小2.7%。與表3中序號3的B腿系固力完全一致。

2)陸側系固

根據W4的輪壓，為使陸側系固力最小，應使C負輪壓減為0，得松弛剛好應設為原重力撓度，即

根據W4輪壓得陸側系固力

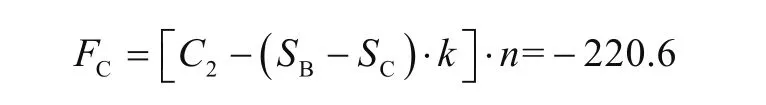
對比表3中序號4的C腿系固力214.6 t，僅大2.8%。

綜上可見，簡化算法與FEA結果差異小于3%，具有很好的精度。

4.4 調整

通過調整松弛量使得海、陸側系固載荷可以一定范圍內調節。如海陸側系固時，為了使不同風向時，海、陸側最大系固載荷相等，可增加某處松弛量，降低該處最大系固載荷，且只能采用增加此處松弛量的辦法。具體方法為：將該處松弛增加X，則此處系固在最大載荷基礎上減少為n·X·k，另一側的系固最大載荷增加為n·X·k。

5 松弛設計

防風系固一般采用螺桿設計以便于碼頭操作，如圖4a所示。為了實現松弛量的調節，在操作時，可先收緊再反轉操作手柄。可根據螺距-松弛量的關系，控制反轉角度或圈數。為了便于檢查松弛量，可在系固聯板設一定長度的長腰孔，如圖4b所示，反轉螺桿使得銷軸頂住長腰孔下極限點。

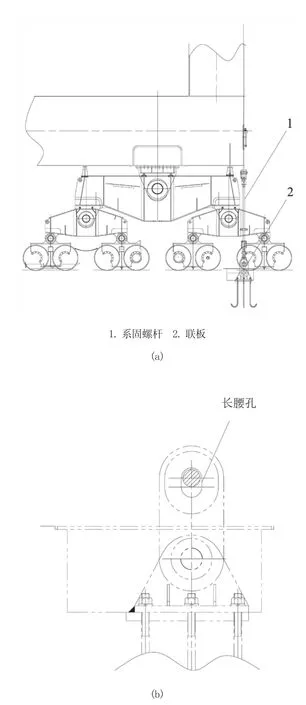
圖4 系固設計

抬腿量的值近視為n·(Δ-S)。抬腿量多少為合適，可視情況定。一方面抬腿降低錨定插入深度，要視碼頭錨定坑的深度是否足夠，否則影響傳遞大車軌道方向水平力。而輪緣是否能脫離軌道，此時要視結構強度是否足夠，必要時可以考慮加高大車輪緣。

6 結論

系固操作時理論上不應收緊。系固收緊是傳統認識的誤區，因為收緊導致了系固載荷的額外增加對起重機安全不利。其載荷與結構剛度和松弛程度有關，調節松弛量可以調節系固載荷分布，并可以降低最大系固力。

本文的簡化算方法建立了系固載荷與結構剛度、幾何尺寸、輪壓、松弛量的定量關系，且具有滿意的精度，適合工程應用。

另外，研究發現大車摩擦力的作用有利于降低最大系固力，抗傾覆裝置則能顯著降低最大系固力。考慮到它們受墊塊間隙，摩擦系數的影響較大，且計算分析復雜，一般情況下不作考慮，可視作安全儲備。