幾何模型在中考數學中的應用與滲透
彭熙
摘要:初中數學教學中,幾何知識的教學所占的比重較大,而解幾何題對培養學生的邏輯思維以及綜合運用數學知識處理問題能力具有良好的促進作用。幾何題業已成為數學中考題中的難點及熱點內容。在初中數學教學中,采用傳統單一的教學模式,會使學生難以深入理解和掌握幾何知識并逐漸失去學習數學的興趣。基于此,數學教師應該學會利用幾何模型開展幾何教學,引導學生更好的觀察和分析圖形,并在復雜圖形中分離出幾何基本模型,降低幾何題的難度,從而提高初中生解題能力。因此,本文對幾何模型在中考數學中的應用進行分析,提出幾何模型在數學教學中應用的有效措施,使得幾何模型教學的效率提升。這樣,將有利于初中生更好的應對中考,獲得較好的數學成績。
關鍵詞:幾何模型;中考;應用
引言
幾何教學內容是初中數學課程中的重要組成部分,也是中考數學經常設置難點的部分。幾何部分學習難度比較大,導致很多初中生難以清晰、有條理地分析其中的各種關系,在中考中無所適從。出現這種問題的關鍵因素就是老師在教學中采用傳統模式,使得學生對幾何知識的認識程度不足,無法有效地分析幾何問題,更找不到解題的切入點。為了提高初中生幾何知識掌握水平和解題能力,初中數學教師需要改變以往教學方式,多利用幾何模型開展教學,帶領學生把握幾何基本模型,再教導學生學會分析復雜的幾何圖形,理清其中的關系,提高學生幾何解題能力,更好的應對中考。
一、幾何模型在中考數學中的應用與滲透
(一)在線段最值解題中的應用
1.幾何模型及分析
點P為直線L外的一個點,點A為直線L上的一個點,讓PA線段值最短。如圖1所示。過點P做垂直于直線L的線,其垂足為點A,這是依據直線以外的一個點和直線上所有點連接的線段中,最短的為垂直線段的原理解決問題,由此可知,直線L上的各點與點P連接的線段中線段AP的最短,這個模型為“垂直段最短”。
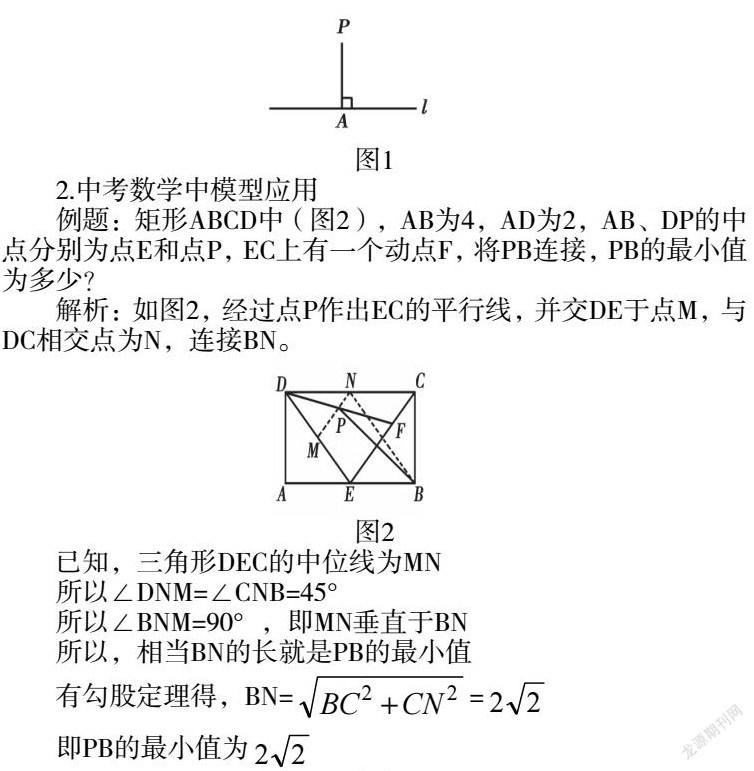
2.中考數學中模型應用
例題:矩形ABCD中(圖2),AB為4,AD為2,AB、DP的中點分別為點E和點P,EC上有一個動點F,將PB連接,PB的最小值為多少?
解析:如圖2,經過點P作出EC的平行線,并交DE于點M,與DC相交點為N,連接BN。
分析:根據題目中的已知條件,點F為EC上的動點,如果點F移動,線段DF也會發生移動,所以,點P也是動點。線段EC為點F的運動軌跡,由于點P為DF的中點,所以,點P運動的軌跡是三角形DEC的中位線MN。這時這道題目就轉化為“垂直線段最短”的幾何模型,在根據此模型的解題思路解答。這種幾何模型的解題方法降低原本題目的難度,使得學生快速且準確的解決數學問題。
(二)反比例函數中的應用
1.幾何模型及原理
點B、D、C在同一條直線上,∠B、∠ADE、∠C均為90°直角,這個模型為“一線三等角”。此幾何模型的解題原理為,∠ABD=∠ADE=∠ECD=90°,那么三角形 ABD 相似于三角形DCE。
2.中考數學的具體應用
例題:已知點A(2,3),點B(0,2),點A在反比例函數 圖形上,做出一條射線AB,并逆時針方向圍繞點A旋轉45°,與反比例函數圖像相交于點C,求點C的坐標。
解析:結合旋轉45度的已知條件,可以想到等腰直角三角形。如圖3所示,將點B作為圓心,按照順時針方向將AB旋轉90°,這時點A正好和直線AC相交于點D,然后作DE垂直于y軸,AF垂直于y軸,證明三角形ABF全等于三角形BDE,即得到點D(1,0),在結合點A(2,3)得知直線AC為y=3x-3。
分析:通過旋轉構造等腰直角三角形,轉化成已知點旋轉90°后的點求坐標問題,學生可以很直觀的聯想到一線三直角構造全等三角形模型,從而求出點的坐標.
二、提升幾何模型在中考數學中應用的措施
(一)加強各圖形以及知識之間的聯系
數學各個部分的知識之間均有一定的聯系,這就需要學生善于總結知識點,實現數學知識運用的融會貫通。初中數學幾何知識學習時,教師應引導學生了解各個圖形之間的相似知識點的聯系,促使學生深入掌握幾何知識。初中幾何解題常用方法為數形結合,這種方法能夠幫助學生正確地理解題意、掌握正確解題思路,同時能夠幫助學生把抽象而復雜的題目變得更為直觀簡單,從而極大地提高學生的解題速度和解題能力。比方說,我們初中數學教師在教授平行四邊形面積內容時,課前可以制作一個可以隨意活動的矩形,在課堂教學中,可以將矩形的對焦點拉動,為學生呈現發生形變的矩形,最終形成一個平行四邊形,以此引導學生將矩形和平行四邊形的知識點和圖形進行聯系,使知識變得更加系統。這些做法,有助于培養學生獨立思考的習慣,有助于培養學生探究問題的能力,有助于提升學生利用抽象思維解決幾何題的水平。
(二)合理使用圖形提高轉化能力
初中幾何教學中,圖形具有關鍵作用。培養學生圖形轉化能力,是初中數學教學的根本任務。初中生空間想象能力不足,分析問題較為片面化,而幾何教學中大部分內容都與圖形有關,學生只有具備良好的圖形轉化能力,才能了解幾何問題的本質,降低幾何問題的難度。因此,初中數學教師在幾何內容教學中應注重學生圖文轉化的能力,幫助他們合理分析問題和解決問題,從而樹立正確的解題意識。例如,在學生知道現有圖形的情況下,了解到AB與CD平行,而且AB= CD,
這時,數學教師應鍛煉學生將文字條件轉化為圖形中內容的能力,要求學生可以準確的在圖形中將條件標注,建立幾何模型,幫助學生更加徹底地明確相關數學概念,從而提高解題能力。
結語
中考復習期間,教師應強化學生幾何模型的應用能力,并不斷挖掘和整合典型的應用案例,讓學生掌握如何在復雜題型中分析出幾何模型,提高學生幾何模型應用水平和解題能力,促使初中生數學水平大大提高,為提高中考總分貢獻應有的力量。
參考文獻:
[1]彭艷輝.探究幾何體模型在初中數學教學中的應用[J].魅力中國,2020(38):58.
[2]胡清山.熟識幾何基本模型實現數學解題化繁為簡研究[J].成才之路,2020(15):84-87.
[3]張寧.提煉幾何模型破解線段最值——基于模型思想求解中考數學試題中線段或線段之和(差)的最值問題[J].理科考試研究(初中版),2020,27(11):11-16.

