基于2個滅點和局部尺度的三維空間尺度估計

周曉慧，丁曉鳳，熊赟暉，彭長歆

基于2個滅點和局部尺度的三維空間尺度估計

周曉慧1，丁曉鳳1，熊赟暉1，彭長歆2

(1. 華南理工大學數學學院，廣東 廣州 510641；2.華南理工大學建筑學院，廣東 廣州 510641)

三維空間尺度估計是三維重建中的一個重要工作，現實世界中也存在一些基于單幅圖像進行三維空間尺度估計的需求。通常情況下，尺度估計需先對相機進行標定。根據單目圖像符合透視原理的特性，提出了一種基于2個滅點和局部尺度信息的方法對相機進行標定，從而得到單目圖像物體中三維空間尺度信息的估計。首先，從單目圖像中選擇2組互相正交的平行線組，得到對應2個滅點的坐標；然后，利用滅點坐標和焦距信息得到世界坐標系和相機坐標系之間的旋轉矩陣，再利用滅點的性質和已知局部尺度信息得到平移向量，完成單目相機的標定；最后，還原二維圖像中像素點對應的三維世界坐標值，計算出圖像中2個像素點在三維空間的尺度信息。實驗結果表明，該方法能有效地對單幅圖像中的建筑物體進行尺度估計。

單幅圖像；滅點；局部尺度信息；相機標定；尺度估計

恢復單幅或多幅二維圖像中建筑物體的三維幾何結構，即三維重建技術[1-3]是計算機視覺的基礎，也是當前人工智能、虛擬現實等眾多前沿領域的研究難點和熱點。其中，現實世界中存在一些基于單幅圖像進行三維重建[4-6]的需求，例如：從古建筑照片復原照片中的建筑信息。要想從單幅照片或少量照片中對建筑物復原出相同大小的建筑物就需要知道需恢復的建筑物體各部分的尺度信息，這幾乎是一個不可能完成的任務。但在已知照片中某些局部尺度的情況下，通過本文的方法，可獲取到照片中一些其他物體的尺度信息。通常情況下，尺度估計需先對相機進行標定[7-9]，確定相機的內部參數，再獲取三維世界坐標和相機坐標變換中的旋轉和平移，之后便可完成一些建筑物體的尺度信息計算工作。由于單目圖像符合透視原理的特性及其計算的復雜性，利用滅點的屬性進行相機標定[10-15]是一個比較合適的方法。

本文在文獻[10]的基礎上提出了利用2個滅點及已知局部尺度進行三維空間尺度估計的方法。該方法只需做出假設：輸入的單目圖像可以供用戶至少選取2組正交的平行線用以計算相應的2個滅點；圖像中包含已知真實尺度的參照物體；投影中心是圖像中心。其步驟如下：

(1) 從單目圖像上選擇2組互相正交的平行線組，計算平行線所構成的2個滅點的坐標；

(2) 通過2個滅點坐標和與平行線組平行的一條已知線段的真實尺度，計算單目圖像相機標定的旋轉矩陣和平移向量；

(3) 將像素坐標轉化為世界坐標，根據三維空間物體各點的世界坐標和拓撲關系，估計三維空間物體的尺度。

1 相關工作

1990年，文獻[11]首次提出利用滅點進行相機標定，并證明了滅點的3個屬性，還根據這些屬性找到了相機內外參數與滅點之間的關系。

文獻[10]利用2個滅點和一已知線段長度進行相機標定和粗略的三維重建，但該方法并未充分利用滅點的性質使得計算略顯繁瑣。文獻[12]提出一種基于滅點的代數測距方法，通過平行共面空間直線的2個正交集即滅點和參考平面上2個不平行線段的長度，可以唯一地確定參考平面上任意2點之間的距離。但該方法固定的模型參數和參考平面的選擇會對尺度估計結果產生不良影響。

文獻[13]在總結滅點屬性的基礎上，提出了一種基于滅點的三維物體重建方法，首先利用滅點計算相機的內、外部參數，再計算出物體上各點的三維空間坐標，然后通過對物體的繪制及紋理映射，實現三維物體的重建。文獻[14]結合三維真實場景中的滅點提取、車道檢測和車輛檢測3個主要步驟，提出了基于攝像機標定的攝像機與正面車輛之間的距離估計方法。文獻[15]提出了一種在人工環境下使用滅點檢測進行自標定的算法，假設主點為圖像的中心，以滿足3個滅點的正交性，用于焦距的估計。但文獻[13,15]基于滅點的標定方法，則要求圖像中存在3組兩兩正交的平行線組，在實際應用中很難滿足該條件，因此應用范圍受到制約。

2 尺度估計流程

本文尺度估計的具體方法如圖1所示，首先在單目圖像上選擇2組互相正交的平行線組，進行相應2個滅點坐標的計算；然后利用計算所得的2個滅點坐標和已知局部尺度信息進行相機標定；最后恢復2組平行線組所張成的平面上任意2點間的尺度信息。

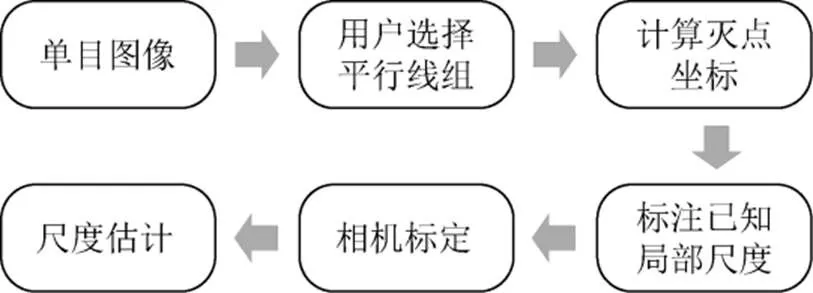
圖1 尺度估計主要流程

2.1 滅點坐標的計算

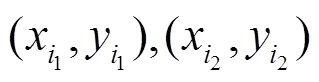
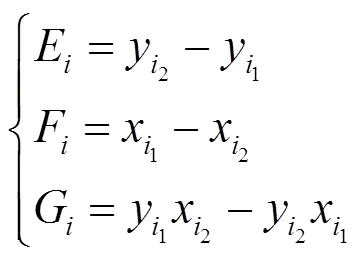
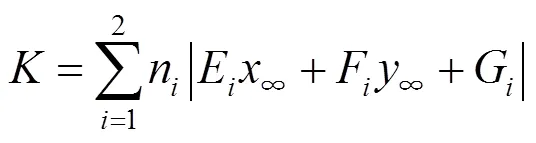
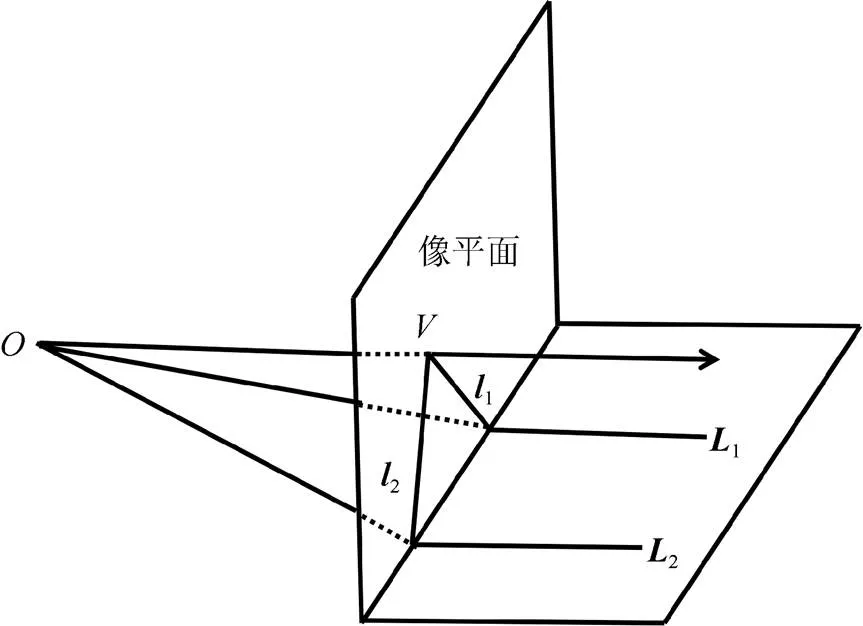
圖2 滅點示意圖

2.2 基于2個滅點和已知局部尺度的相機標定

在小孔成像的基礎上，相機模型的內外參數決定了像素坐標、圖像坐標、相機坐標和世界坐標之間的轉換。利用滅點的屬性進行相機標定需做如下假設：

(1) 輸入的單目圖像可以供用戶至少選取2組正交的平行線用以計算相應的滅點；

(2) 圖像中包含已知真實尺度的參照物體；

(3) 投影中心是圖像中心。

2.2.1 旋轉矩陣的計算

如圖3所示，世界坐標系以點作為原點，由3個方向的正交基向量,,(=×)構成：=(,,,)；相機坐標系以點為原點，由3個方向的正交基向量,,(=×)構成：=(,,,)；像平面坐標系為=(,,)，其中點為相機中心在像平面上的正交投影。世界坐標系到相機坐標系的旋轉矩陣為，則有

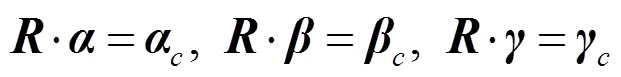
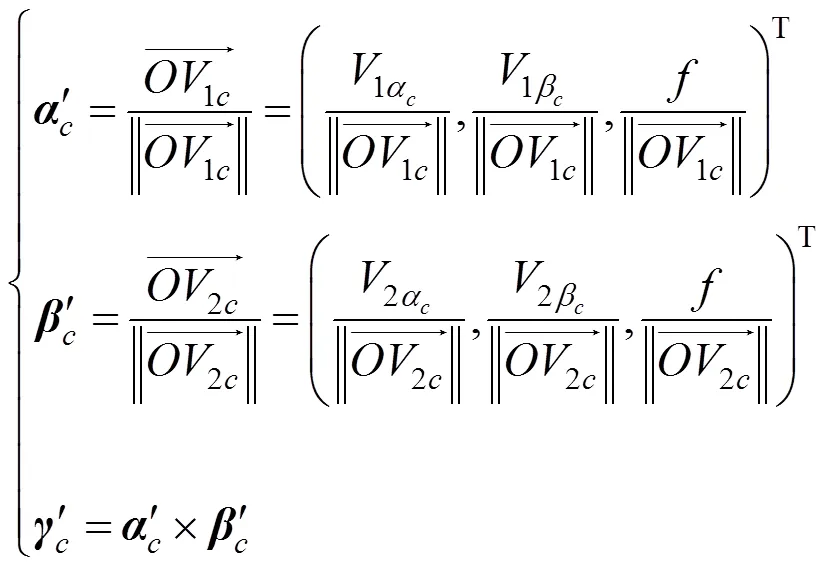
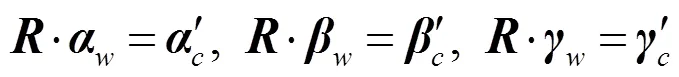
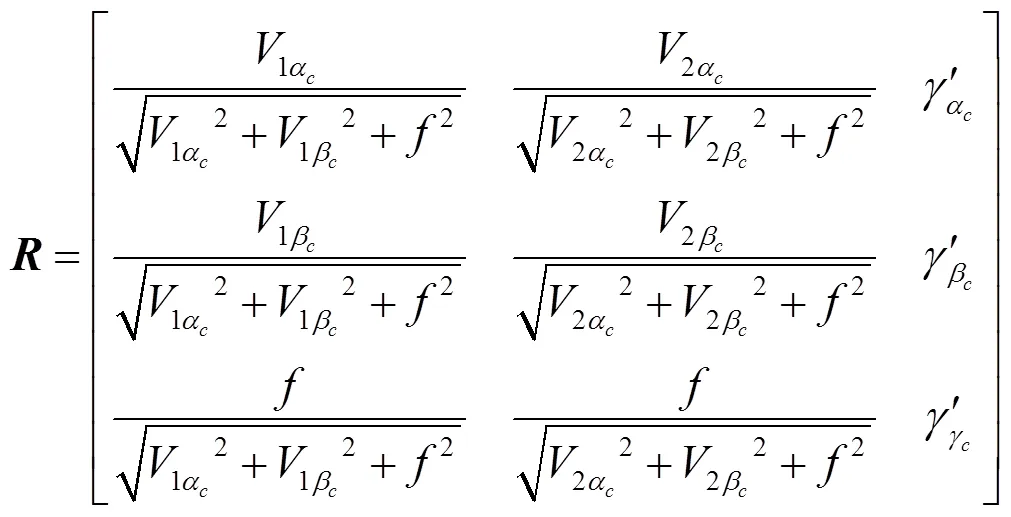
2.2.2 平移向量的計算

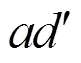
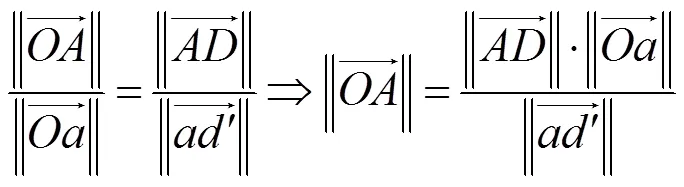
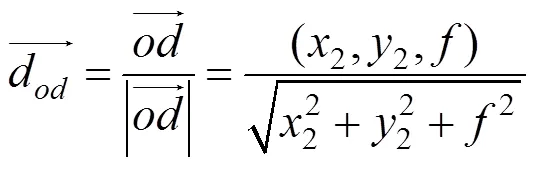
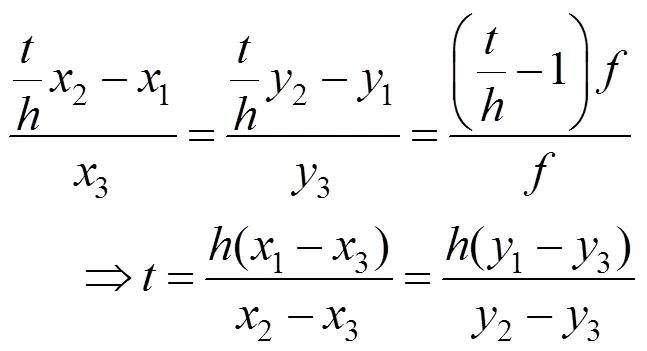
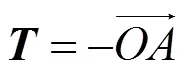
2.3 建筑物體估計尺度的計算

如圖5所示，像素坐標[,]向世界坐標[X,Y,Z]的轉化實質是：先由像素坐標轉化為圖像坐標，再由圖像坐標轉化為相機坐標，最后由相機坐標轉化至世界坐標。

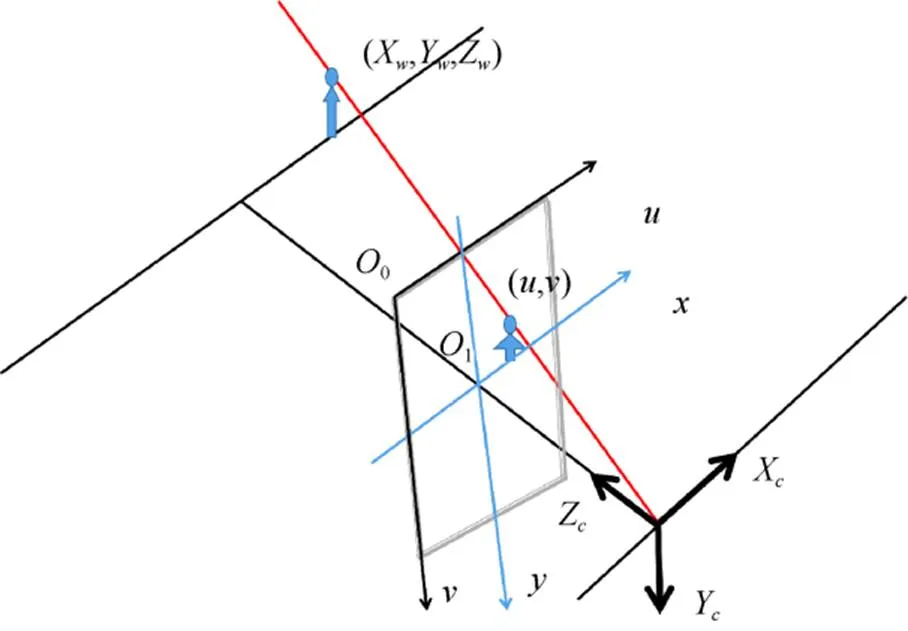
圖5 像素坐標系與世界坐標系示意圖

以圖像左上角為原點0建立笛卡爾直角坐標系-(單位：像素)，圖像在計算機數組中的列數與行數是像素的橫坐標和縱坐標。定義圖像坐標系的原點1為成像平面和相機光軸的交點且在-坐標系下的坐標設為(0,0)；軸與軸平行，軸與軸平行；每個像素在橫軸和縱軸上的物理尺寸為d和d。則圖像中每個像素在-坐標系下與在-坐標系下的坐標之間存在如下關系，即

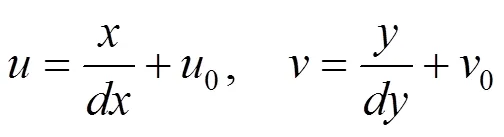
假設圖像坐標系以毫米作為物理單位，則的單位為毫米/像素，/的單位為像素，式(10)可表示為

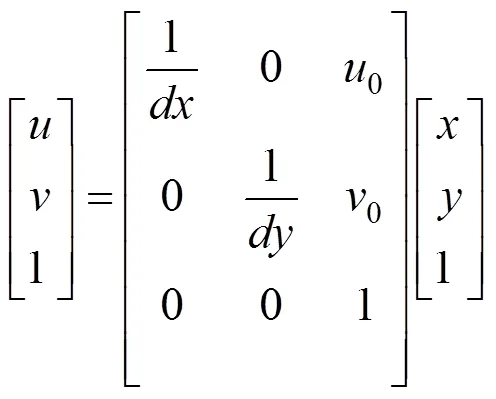
至此完成了像素坐標到圖像坐標的轉化。

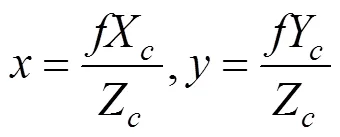
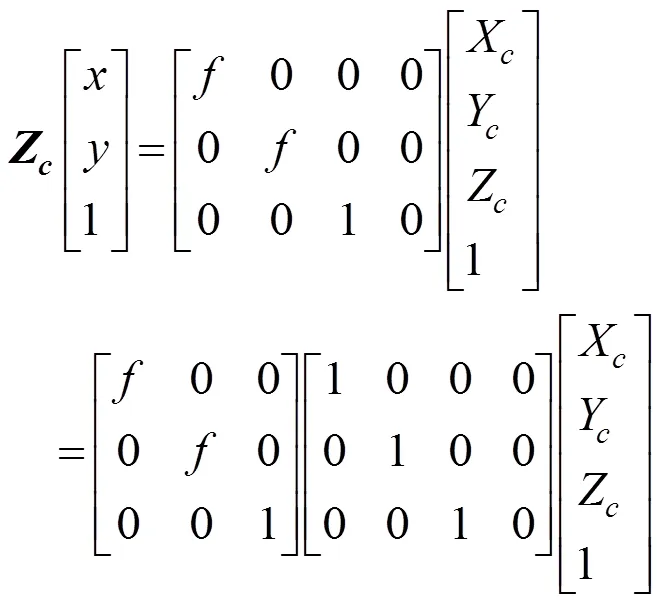
可得：和。至此完成了像素坐標到相機坐標的轉化。

而相機坐標到世界坐標的轉化實際上是一種剛體變化，對坐標進行旋轉和平移操作即可得到轉化關系，二者之間的剛體變換數學表示為

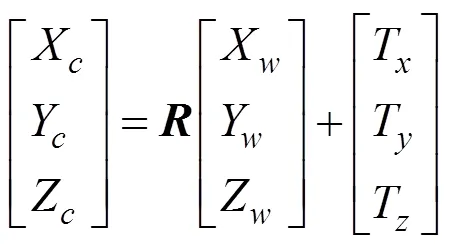
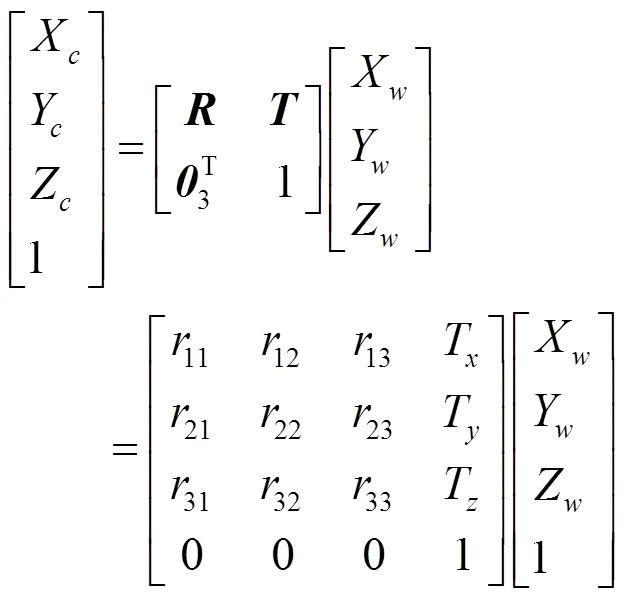
將上述所示的轉換過程合并可得像素坐標和世界坐標之間的數學關系，即

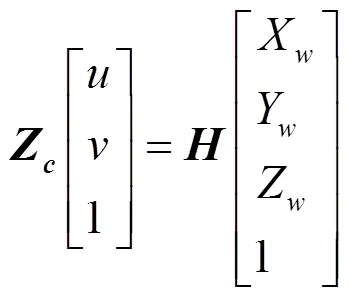
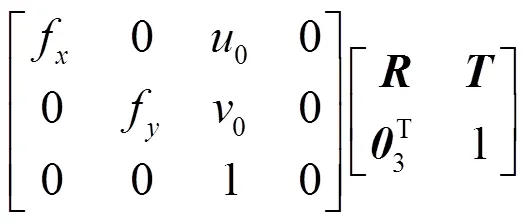
在計算的過程中，假設生成滅點的2組平行線組所在平面的世界坐標值是相同的，則推導出二維圖像點的三維世界坐標為

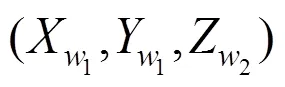
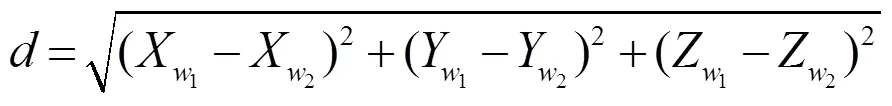
3 算法實現及實驗結果分析

3.1 算法實現

算法實驗使用CPU i5-8500，8 G內存Windows10系統中Visual Studio 2015環境和Python3.7環境實現主要代碼，還采用了OpenCV，Numpy，PIL等第三方代碼庫。實驗主要研究對象是室外場景單目圖像，其包含一些已知尺度信息的參照物(如已知尺度信息的墻磚或地磚)。

在單幅單目圖像中，基于2個滅點和局部尺度信息的三維空間尺度估計算法(3D spatial scale estimation，SSE)步驟如下：

輸入：單目圖像和一條線段的真實尺度值。

輸出：圖像建筑尺度估計值。

步驟1.用戶從圖像中選擇2組互相正交的平行線組，計算出2個滅點的坐標；

步驟2. 通過2個滅點坐標和圖像中這2組平行線所在平面中的一條已知線段的真實尺度，計算單目圖像相機標定的旋轉矩陣和平移向量；

步驟3. 將像素坐標轉化為世界坐標，即可得到這2組平行線所在平面上建筑物體的估計尺度。

3.2 誤差定義

通過人工實地測量的方式得到圖像參照物的真實尺度值，再利用算法的計算結果得到圖像建筑物的真實尺度估算值。用相對誤差來對SSE算法的有效性進行評估。

3.3 實驗結果及分析

用戶對于平行線組的選取和相應的滅點計算如圖7所示。圖中紅色和綠色2組平行線在真實場景中互相正交，并確定了尺度估計所需的2個滅點。對于每個滅點，用戶(用鼠標)選擇一組建筑物上存在的平行線。為了使選擇更加容易，輸入圖像是超大分辨率原圖，且未進行縮小。具體的滅點坐標計算見2.1節。

圖7 滅點計算示意圖

圖8中的#1，#2和#3行表示同一建筑物不同視角下的圖像。圖8(a)為同一個建筑物體不同觀測角度下所拍攝的圖像；圖8(b)為用戶在相應圖像上選擇的2組正交平行直線(紅、綠線組)結果，用以計算平行線組形成的滅點坐標；圖8(c)為單目圖像建筑物體尺度估計的結果，其中紅線為建筑物體尺度估計的范圍。

圖8 同一建筑物體不同視角下的尺度估計((a)單目圖像；(b)平行線選擇；(c)尺度估計結果)

表1顯示了同一建筑物不同視角下SSE算法的實驗誤差結果。由表1可知，SSE算法在不同視角下對同一建筑物體進行尺度估計均可獲得較好的結果。

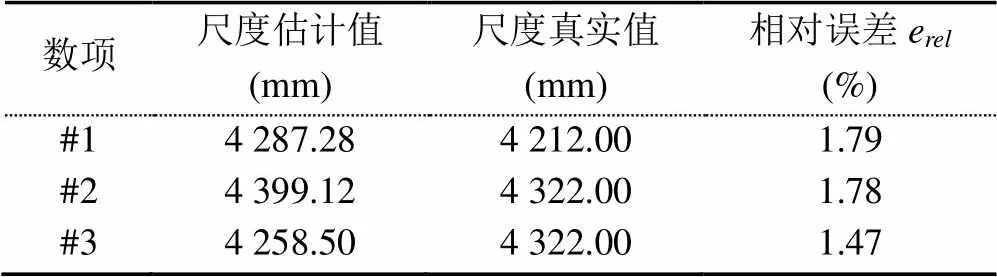
表1 同一建筑物體不同視角下尺度估計的誤差

圖9為不同方法對同一建筑物體進行尺度估計的比較結果。圖9(a)為建筑物體室外場景的單目圖像；圖9(b)為SSE算法的尺度估計效果，其中紅線區域即為建筑物體尺度估計的范圍；圖9(c)為文獻[12]運用滅點和單應性矩陣方法得到的尺度估計效果；圖9(d)為文獻[13]運用3個滅點進行相機標定后的尺度估計效果。其中圖9(d)前2行尺度估計值在圖像上沒有展示的原因是，圖像中無法準確找到3組兩兩正交的平行線組。

圖9 不同算法間建筑物體尺度估計的比較((a)單目圖像；(b) SSE算法；(c)文獻[12]算法；(d)文獻[13]算法)

表2顯示了不同方法對同一建筑物體進行尺度估計的誤差結果，其中“-”表示未得到相應估計值。從表中可以看出，SSE算法效果較好，文獻[12-13]所提出的尺度估計方法誤差相對較大。其中文獻[12]的方法是基于提前設置好的相機模型參數、參考平面和垂直于參考平面的一個參照尺度，進行與參考平面垂直平面上的相關尺度估計。這種固定的模型參數和參考平面的選擇會對估計結果產生一定的影響。而文獻[13]的方法則是基于3組兩兩垂直的滅點對相機進行標定從而得到待測物體的尺度比例關系。理論上來說，3個滅點相較于2個滅點進行標定應該更加精準，但是在真實場景的圖像中可能因為很難找到相互正交的3組平行線形成的3個滅點，反而造成更大的誤差。文獻[13]算法需要采用2張同一物體在同一方向、不同角度下的圖像來對其進行優化，研究更多的是針對建模和仿真，主要是恢復圖像中物體尺度的比例關系，更多的是滿足虛擬現實系統的需求，因此在對真實場景的單目圖像中物體進行估計時會造成較大的誤差。

表2 不同方法進行建筑物體尺度估計的誤差

4 結束語

由于單目圖像符合透視原理的特性，用滅點對圖像建筑物體進行尺度估計是一個比較好的方法。在實際應用中，有些建筑圖像(包括古建筑殘存的圖像)找不到符合要求的3組兩兩正交的平行線組形成的滅點，因此無法用基于3個滅點的算法來計算。對于這些圖像，如果可以從圖像中找到一些已知尺度的物體(如:某個時期古建筑中采用固定尺寸的磚塊、地磚和瓦片等)，通過這些已知尺度物體信息，再結合2個滅點就可對圖像中建筑物體的某些區域進行尺度估計。基于該思想本文提出了利用2個滅點和局部尺度信息進行三維空間尺度估計的方法。

實驗結果表明，與文獻[12-13]的尺度估計算法相比較，本文算法有比較好的計算結果。并且該算法對輸入的圖像限制和所需的幾何約束較少，適用于更多的場景，泛化性高。但是由于本文算法存在已知尺度線段需平行于某一組所選平行線的限制條件，實際應用中如果已知尺度線段不平行于任何一組平行線，可以考慮將其投影到其中一組平行線后再進行平移向量的計算。同時，因為本文算法是基于傳統滅點理論來進行尺度估計，故和其他滅點算法一樣，缺乏對圖像中各像素點的深度估計，只能計算2組平行線所在平面上的2個像素點間的距離，還無法做到計算圖像中任意2點間的距離。

[1] 董鵬輝, 柯良軍. 基于圖像的三維重建技術綜述[J]. 無線電通信技術, 2019, 45(2): 115-119.

DONG P H, KE L J. Overview of 3D reconstruction techniques based on images[J]. Radio Communications Technology, 2019, 45(2): 115-119 (in Chinese).

[2] LIU C X, KONG D H, WANG S F, et al. Deep3D reconstruction: methods, data, and challenges[J]. Frontiers of Information Technology & Electronic Engineering, 2021, 22(5): 652-672.

[3] TAHIR R, SARGANO A B, HABIB Z. Voxel-based 3D object reconstruction from single 2D image using variational autoencoders[J]. Mathematics, 2021, 9(18): 2288.

[4] LI G Q, WU Z H, LIU Y X, et al. 3D hand reconstruction from a single image based on biomechanical constraints[J]. The Visual Computer, 2021, 37(9-11): 2699-2711.

[5] YAN C G, SHAO B Y, ZHAO H, et al. 3D room layout estimation from a single RGB image[J]. IEEE Transactions on Multimedia, 2020, 22(11): 3014-3024.

[6] CHEN Y, TU Z, KANG D, et al. Joint hand-object 3D reconstruction from a single image with cross-branch feature fusion[J]. IEEE Transactions on Image Processing, 2021, 30: 4008-4021.

[7] MAALEK R, LICHTI D D. Automated calibration of smartphone cameras for 3D reconstruction of mechanical pipes[EB/OL]. [2021-07-10]. https://arxiv.org/abs/2012.02899.

[8] 王沛, 鐘凱, 顏福鹍, 等. 基于相位移編碼圓的相機離焦快速標定方法[J]. 光學技術, 2021, 47(4): 494-499.

WANG P, ZHONG K, YAN F K, et al. Fast calibration method of camera defocus based on phase shift coding circle[J]. Optical Technique, 2021, 47(4): 494-499 (in Chinese).

[9] 赫美琳, 高明慧, 李爽, 等. 一種單目相機標定算法研究[J]. 數字通信世界, 2018(5): 11-14.

HE M L, GAO M H, LI S, et al. Research on a monocular camera calibration algorithm[J]. Digital Communication World, 2018(5): 11-14 (in Chinese).

[10] GUILLOU E, MENEVEAUX D, MAISEL E, et al. Using vanishing points for camera calibration and coarse 3D reconstruction from a single image[J]. The Visual Computer, 2000, 16(7): 396-410.

[11] CAPRILE B, TORRE V. Using vanishing points for camera calibration[J]. International Journal of Computer Vision, 1990, 4(2): 127-139.

[12] WANG G H, WU Y H, HU Z Y. A novel approach for single view based plane metrology[C]//2002 International Conference on Pattern Recognition. New York: IEEE Press, 2002: 556-559.

[13] 余燁, 劉曉平. 基于滅點的三維物體重建[J]. 系統仿真學報, 2008, 20(15): 4069-4072.

YU Y, LIU X P. 3D object reconstruction using vanishing points[J]. Journal of System Simulation, 2008, 20(15): 4069-4072 (in Chinese).

[14] BOUGHARRIOU S, HAMDAOUI F, MTIBAA A. Vehicles distance estimation using detection of vanishing point[J]. Engineering Computations, 2019, 36(9): 3070-3093.

[15] LEE S J, HWANG S S. Fast and accurate self-calibration using vanishing point detection in manmade environments[J]. International Journal of Control, Automation and Systems, 2020, 18(10): 2609-2620.

3D spatial scale estimation based on two vanishing points and local scale

ZHOU Xiao-hui1, DING Xiao-feng1, XIONG Yun-hui1, PENG Chang-xin2

(1. School of Mathematics, South China University of Technology, Guangzhou Guangdong 510641, China; 2. School of Architecture, South China University of Technology, Guangzhou Guangdong 510641, China)

3D spatial scale estimation is of great significance to 3D reconstruction, and is in demand in the real world in the case of a single image. Generally, the camera must be calibrated before the scale estimation. According to the perspective principle of the monocular image, a method based on two vanishing points and local scale information was proposed to calibrate the camera, thereby obtaining the estimation of the 3D scale information in the monocular image. Firstly, two orthogonal groups of parallel lines were selected from the monocular image to produce the coordinates of two vanishing points. Then the rotation matrix between the world coordinate system and the camera coordinate system was yielded using the vanishing point coordinate and the focal length information. The translation vector was also acquired through the property of vanishing point and the known local scale information. Finally, the 3D world coordinates corresponding to the pixels in the 2D image were restored to calculate the 3D scale information. Experimental results show that this method can effectively estimate the scale of building objects in a single image.

single image; vanishing point; local scale information; camera calibration; scale estimation

TP 391

10.11996/JG.j.2095-302X.2022030370

A

2095-302X(2022)03-0370-07

2021-09-02；

2021-09-28

2 September，2021；

28 September，2021

國家自然科學基金項目(51978271)

National Natural Science Foundation of China (51978271)

周曉慧(1998-)，女，碩士研究生。主要研究方向為相機標定和三維重建。E-mail：autoffier@163.com

ZHOU Xiao-hui (1998-), master student. Her main research interests cover camera calibration and 3D reconstruction. E-mail：autoffier @163.com

熊赟暉(1972–)，男，副教授，博士。主要研究方向為圖像和視頻處理、幾何建模和處理、3D重建、3D打印等。E-mail：yhxiong@scut.edu.cn

XIONG Yun-hui (1972–)，professor, Ph.D. His main research interests cover image and video processing, geometry modeling and processing, 3D reconstruction, 3D printing, etc. E-mail：yhxiong@scut.edu.cn