一“點(diǎn)”牽想象 全面引運(yùn)動(dòng)
——《圖形的運(yùn)動(dòng)》總復(fù)習(xí)教學(xué)

文|金 奎

【教學(xué)內(nèi)容】

人教版六年級(jí)下冊(cè)第92、93頁(yè)。

【教學(xué)過(guò)程】

一、給一點(diǎn)，自由想象

1.提出問(wèn)題。

師：同學(xué)們，這節(jié)課我們來(lái)復(fù)習(xí)圖形的運(yùn)動(dòng)。回憶一下，小學(xué)階段我們學(xué)過(guò)的圖形運(yùn)動(dòng)有哪些？

生：有平移、旋轉(zhuǎn)、軸對(duì)稱(chēng)、放大與縮小。

師：讓我們張開(kāi)想象的翅膀，一起進(jìn)入圖形運(yùn)動(dòng)的世界。請(qǐng)看：有這樣一個(gè)三角形ABC，假如這個(gè)點(diǎn)是三角形ABC運(yùn)動(dòng)后其中的某個(gè)頂點(diǎn)的新位置。你知道它可能是怎么運(yùn)動(dòng)的嗎？

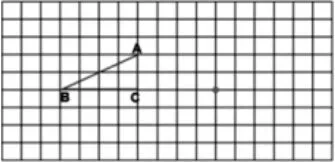
【設(shè)計(jì)意圖：先讓學(xué)生回憶圖形運(yùn)動(dòng)的多種方式，不斷喚醒舊知；再通過(guò)創(chuàng)設(shè)“給出運(yùn)動(dòng)后某個(gè)頂點(diǎn)的新位置，研究可能是怎么運(yùn)動(dòng)的”這個(gè)問(wèn)題，給了學(xué)生自由想象的思維空間。】

2.分層反饋。

（1）反饋。

層次一：平移。

師：通過(guò)分類(lèi)，來(lái)說(shuō)說(shuō)這兩幅圖是怎么平移得到的？

生1：第一幅是把三角形ABC向右平移4格后得到的。

生2：第二幅則是把三角形ABC向右平移8格得到的。

師：因?yàn)槠揭频木嚯x不一樣，所以最后的位置也不一樣。在描述平移的時(shí)候說(shuō)清楚方向和距離很重要。

層次二：旋轉(zhuǎn)。

師：這幅圖是怎么得到的？

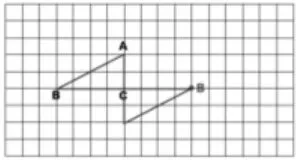
生：把三角形ABC繞點(diǎn)C逆時(shí)針旋轉(zhuǎn)180度后得到，也可以把三角形ABC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)180度后得到。

小結(jié)：旋轉(zhuǎn)時(shí)，要說(shuō)清楚繞點(diǎn)、旋轉(zhuǎn)方向、旋轉(zhuǎn)角度，缺一不可。

層次三：軸對(duì)稱(chēng)。

師：同樣是軸對(duì)稱(chēng)圖形，為什么第一幅這個(gè)點(diǎn)是點(diǎn)B的對(duì)應(yīng)點(diǎn)，而第二幅是點(diǎn)C的對(duì)應(yīng)點(diǎn)？

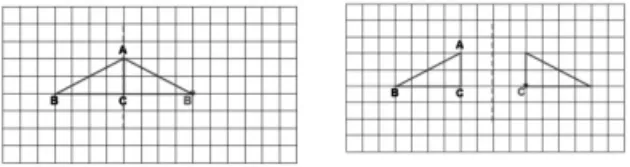
生：第一幅對(duì)稱(chēng)軸在AC的位置，第二幅對(duì)稱(chēng)軸則是在AC往右兩格的位置。

師：軸對(duì)稱(chēng)的特點(diǎn)是對(duì)稱(chēng)點(diǎn)到對(duì)稱(chēng)軸的距離相等，并且連線與對(duì)稱(chēng)軸垂直。

層次四：放大與縮小。

師：下圖又是怎么運(yùn)動(dòng)的？

生：三角形ABC按2∶1放大后的圖形。

師：底放大到原來(lái)兩倍的同時(shí)，高也相應(yīng)地放大到原來(lái)的兩倍，縮小也是同樣的道理。

（2）概括。

師：剛才我們通過(guò)三角形ABC回顧了圖形的運(yùn)動(dòng)。那么它們之間有什么相同點(diǎn)和不同點(diǎn)呢？

生1：無(wú)論是哪一種運(yùn)動(dòng)，運(yùn)動(dòng)前后圖形的形狀都沒(méi)有發(fā)生改變。

生2：剛才畫(huà)這些圖形的時(shí)候我們都是按照先找點(diǎn)、再描點(diǎn)、最后連線的方法，所以畫(huà)法也相同。

生3：不同點(diǎn)是：經(jīng)過(guò)平移、旋轉(zhuǎn)、軸對(duì)稱(chēng)，圖形的大小不變，只改變了位置；而經(jīng)過(guò)放大與縮小后，圖形的大小改變了。

板書(shū)：

?

【設(shè)計(jì)意圖：大多學(xué)生會(huì)把這一點(diǎn)想象成B點(diǎn)或C點(diǎn)的新位置，這樣正好可以牽出各種運(yùn)動(dòng)的方式，在追問(wèn)中及時(shí)復(fù)習(xí)運(yùn)動(dòng)的特點(diǎn)及要素。為了把這些分支加以整合，引導(dǎo)學(xué)生充分觀察、對(duì)比運(yùn)動(dòng)方式，概括出不同點(diǎn)與相同點(diǎn)，真正體現(xiàn)出總復(fù)習(xí)課“聯(lián)”“融”的意味。】

二、求變式，延伸想象

1.A到目標(biāo)位。

師：在剛才的創(chuàng)造中，我們是把點(diǎn)B或點(diǎn)C運(yùn)動(dòng)到這一點(diǎn)，現(xiàn)在請(qǐng)你再次想象：能不能讓點(diǎn)A運(yùn)動(dòng)到這點(diǎn)？

生1：先把三角形ABC向右平移4格，再向下平移2格。

生2：先把三角形ABC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)90度，再向右平移2格。

生3：先把三角形ABC繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90度，再向右平移4格，最后向下平移2格。

2.以AB為對(duì)稱(chēng)軸。

師：跳出這一點(diǎn)來(lái)繼續(xù)想象，假如三角形ABC是軸對(duì)稱(chēng)圖形的其中一半，以AB邊為對(duì)稱(chēng)軸，你能找到點(diǎn)C的對(duì)稱(chēng)點(diǎn)嗎？

生：我們可以利用軸對(duì)稱(chēng)特點(diǎn)找到點(diǎn)C的對(duì)稱(chēng)點(diǎn)。

3.以整體為一個(gè)圖形。

師：如果以D點(diǎn)為繞點(diǎn)，把三角形ABC逆時(shí)針旋轉(zhuǎn)90度，哪一幅圖是正確的呢？

生：我們可以把這個(gè)點(diǎn)和點(diǎn)C連起來(lái)，整個(gè)圖形看作小旗比較方便，所以第二幅是正確的。

師：把看不見(jiàn)的圖形想象成了看得見(jiàn)的圖形，想象的確能幫助我們更好地學(xué)習(xí)數(shù)學(xué)。

【設(shè)計(jì)意圖：一“點(diǎn)”的價(jià)值不僅僅是運(yùn)動(dòng)特點(diǎn)的再現(xiàn)，更是有限的素材無(wú)限地使用。為了引發(fā)學(xué)生深層次的思維，教師引導(dǎo)學(xué)生“這一點(diǎn)如果是A點(diǎn)運(yùn)動(dòng)后的新位置，又可以怎么運(yùn)動(dòng)？”進(jìn)行質(zhì)疑，這樣就可以從運(yùn)動(dòng)組合的角度加以理解；斜的對(duì)稱(chēng)軸課本只作介紹，為了體現(xiàn)總復(fù)習(xí)課適當(dāng)提升的要求，通過(guò)改變對(duì)稱(chēng)軸的位置進(jìn)一步拓展課本知識(shí)；通過(guò)D點(diǎn)為繞點(diǎn)，跳出原有“點(diǎn)的位置”的研究框架，轉(zhuǎn)入整個(gè)圖形的運(yùn)動(dòng)。此時(shí)的選擇已是“無(wú)線”化“有線”，并再一次突破像小旗這類(lèi)看上去簡(jiǎn)單、實(shí)則無(wú)載體依靠的難點(diǎn)。】

三、創(chuàng)練習(xí)，豐富想象

1.選擇題。

（1）下面（ ）張撲克牌，旋轉(zhuǎn)180°后看到的與原來(lái)相同。

2.填空題。

①△ABC繞點(diǎn)C順時(shí)針旋轉(zhuǎn)150°，點(diǎn)B正好落在長(zhǎng)方形CDEF的DE邊上，那么∠1= °

②下圖中，右邊三角形是左邊三角形沿著對(duì)稱(chēng)軸畫(huà)出的軸對(duì)稱(chēng)圖形。根據(jù)圖中信息，點(diǎn)A的位置用數(shù)對(duì)表示是（ ）。

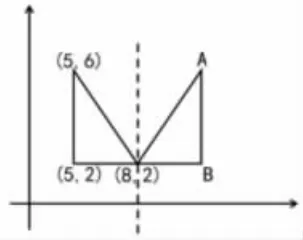
A.（6，10） B.（10，6）

C.（6，11） D.（11，6）

3.面積計(jì)算。