核心素養下小學數學滲透模型思想策略探究

陳　靈

核心素養下小學數學滲透模型思想策略探究

陳靈

（福建省泉州市鯉城區實驗小學，福建泉州362000）

數學核心素養包括數學建模、數學運算、直觀想象以及數據分析等內容，其中數學建模乃是核心素養的主要內容之一，是小學數學教學非常重要的任務，也是提高學生分析問題能力、解決問題能力，培養學生數學知識應用意識的重要內容。在新課改要求下，廣大數學教師當重視學生建模能力培養。本文以小學數學教學為例，聚焦數學核心素養要求，探討如何在小學數學中培養學生模型思想。

小學教育；數學教學；核心素養；模型思想

《義務教育數學課程標準》（2011年版）對模型思想進行了詳細論述，強調模型思想的建立是學生體會和理解數學與外部世界聯系的基本途徑。數學模型思想是學生在感知數學模型、建立數學模型、應用數學模型的過程中逐步形成的一種思維模式，是學生思維發展的直接體現，是需要學生在數學學習過程中觀察、感知、探索、總結、歸納和應用的。在小學數學教學中融合數學模型思想旨在促進學生抽象思維發展，為提升學生數學核心素養奠定基礎。基于此，數學教師也應當充分結合小學生認知水平、理解能力、思維發展規律以及小學數學教材大綱要求，創造性地將數學模型思想融合到數學教學過程中，以數學教學促進學生思維能力發展。

一、小學數學教學中加強學生模型思想培養的意義

（一）促進學生數學思維發展

數學思想融合到小學數學教學中的重要步驟是引導學生建立數學模型，而建模這一過程其實就是學生將抽象數學概念與實際問題建立聯系并互相轉化的過程，需要學生充分結合已有認知經驗，合理應用數學變量、數學公式、數學概念。整個過程幫助學生實現了知識內化和吸收，讓學生對數學知識的理解更透徹，邏輯思維和應用能力得到充分發展。因此，從這一角度而言，數學模型思想融合到小學數學教學中是有助于學生數學思維發展的。

（二）提高學生解決問題的能力

模型思想的本質在于將數學問題簡化，其最終目的指向“問題解決”。將模型思想融合到小學數學教學之中也是為了引導學生建立數學模型，應用數學模型解決實際問題。當學生具有一定建模能力之后，自然能夠將看似復雜的數學問題簡單化，靈活機智地運用所學數學知識解決實際問題，從而提高自身解決問題的效率。

（三）增強學生運用知識的意識

學以致用是學習的最終落腳點，培養學生應用意識也是數學新課標以及數學核心素養對廣大教師提出的根本要求。將數學模型思想融合到小學數學教學之中無疑是迎合了新課標和核心素養發展趨勢，有利于引導學生將生活實際問題與數學知識高度關聯。比如《圖形與幾何》教學中，教師引導學生將拱形原理與“趙州橋”聯系；學習多種幾何圖形時，可引導學生聯系樓盤開放商建立的“沙盤模型”……通過關聯生活的教學讓學生發現數學知識在生活中的實際應用，也促使學生主動到生活中探尋數學的“影子”，喚起學生主動學習和應用數學知識的意識。

二、基于模型思想的小學數學教學策略

（一）立足于數學教材，引導學生認識數學模型

培養學生數學建模能力的前提是學生對模型有初步了解，認識多種數學模型。所以，在小學數學教學中，數學教師首先應引導學生體驗數學模型思想，思索和分析各種不同類型的數學模型，為學生主動搭建和應用數學模型打下堅實基礎。結合筆者對小學生認知水平、理解能力、思維發展現狀的了解來看，當前小學數學教學中可重點引導學生認識如下幾種數學模型：

一是公式模型。數學教材中所有公式的本質都是一種數學模型，比如，路程=時間×速度；總價=單價×數量；矩形的面積=長×寬，長方體的體積=長×寬×高=底面積×高……可以說公式模型是最基礎和簡單的模型，也是學生可以直接運用的一種數學模型。這種模型能夠幫助學生快速解決實際問題，提高學生解決問題的效率。在小學數學新知教學中，數學教師當有意識地滲透公式模型思想，引導學生認識多種公式模型。

二是方程模型。方程模型在小學高年級數學教材中體現較多，其本質是學生結合實際問題列出方程，并解決實際問題。方程模型中引出了未知數，能夠幫助學生順向推導和分析問題，快速找到隱藏在數學問題中的未知量和已知量的數學關系，從而搭建出完整的數學模型。這種數學模型廣泛應用于應用問題中，搭建和應用這種模型有助于培養學生數學閱讀能力、信息收集與整合能力、數據分析與處理能力。

三是幾何模型。幾何模型是用幾何概念描述數學物體形狀的一種模型，是小學數學教材中廣泛應用的一種模型。幾何模型的建立過程是運用數學概念、定理、公式將實際問題抽象成簡單幾何圖形的過程，充分體現了數形結合思想，也有利于學生對數學抽象、概括思維發展。

（二）重視過程教學，引導學生開展數學建模活動

讓學生經歷建模過程是培養學生模型思想必不可少的環節。數學新課標明確強調了學生自主體驗的重要性，要求廣大教師重視“過程教學”，盡可能給學生提供一個發現、探索、總結知識的過程，讓學生在親歷中發現規律，總結結論，解決問題。因此，數學教師應重視教學過程，引導學生開展數學建模活動。具體如何操作呢？數學新課標也給教師們指明了方向：“問題情境——建立模型——求解驗證”，借助這三大環節開展建模探究活動，讓學生能夠對數學模型有更深層次理解。當然，在這一過程中，數學教師也應該扮演好學生的引導者、幫助者角色，注意提醒和點撥學生，引導學生自主思考、合作探究、交流分享，讓學生真正在過程中實現思維碰撞，在過程中發現規律，在過程中解決問題，在過程中獲得模型思想的本質感悟。文章以小學六年級下冊《自行車里的數學》這一內容為例，進行了如下嘗試：

環節一：問題情境

教師談話導入情境：我國是一個自行車大國，每天來回穿梭在街頭的自行車不計其數，同學們有沒有發現自行車里也有很多數學知識呢？你從自行車里了解到了哪些數學知識？鼓勵學生結合自身日常觀察，說一說自行車相關知識。比如，啟發學生從自行車的種類（普通自行車、變速自行車、山地自行車等）角度談論；也可以鼓勵學生將自信車的前后輪與“圓”這一知識建立聯系，引導學生按照車輪直徑分類；還可以啟發學生按照使用對象分類：男車、女車、童車。待激活學生學習熱情后，教師進一步設置問題：自行車是怎樣前行的呢？鼓勵學生聯系個人生活經驗以及所學數學知識，小組內互相說一說，然后總結結論。為進一步激活學生數學思維，教師繼續追問：蹬一圈車輪就轉一圈，走的路即是車后輪的一周周長，你認為對嗎？前齒輪轉一圈，后齒輪轉多少圈呢？引導學生合作完成下表（表1）。

表1

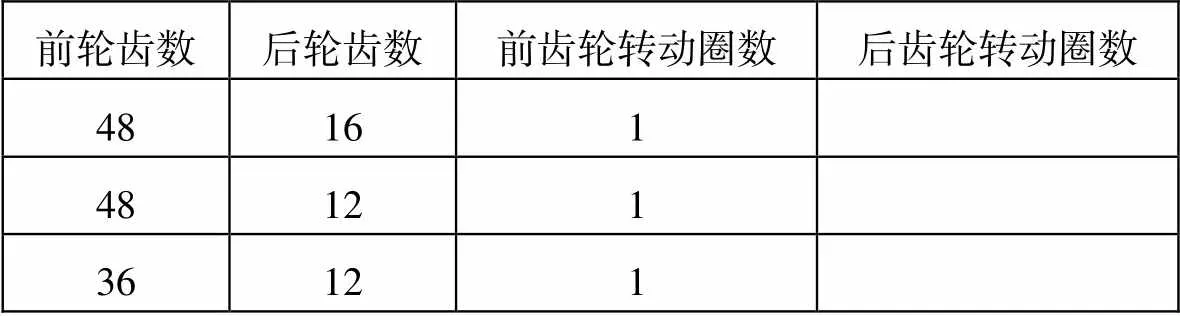
前輪齒數后輪齒數前齒輪轉動圈數后齒輪轉動圈數 48161 48121 36121

環節二：建立模型

建立模型是最關鍵的一步。在引導學生探究數學模型的過程中，數學教師應走出傳統“灌輸式”教學模式的束縛，避免直接告訴學生數學規律、數學答案。相反，教師更應該引導學生主動探索數學規律，建立數學模型。所以，在學生針對上述問題情境有進一步探究之后，數學教師要有意識地引導學生將實際問題與數學知識建立直接聯系。

首先教師追問學生：從上述表格數據可以發現什么？啟發學生將實際問題轉化為已經學習過的數學知識，引導學生將實際問題轉化為“圓”“比例”“排列組合”等數學知識，建立如下數學模型：

其次教師提出新的問題：蹬一圈，自行車能走多遠？請學生談一談自己解決這一問題的方法和發現。

借助已有知識經驗，學生很容易找到解決問題的方法：測量（差距較大）和計算。

在這一環節中，教師充分尊重學生的主體地位，將探索知識的主動棄教給學生，讓學生主動從數學的角度分析生活問題，建立數學模型，讓學生真正發現“蹬同樣多的圈數，自行車走的距離與車輪（半）直徑、前后齒輪齒數的比值有關”。

環節三：求解驗證

建立數學模型之后，最重要的一步就是引導學生利用數學思想、數學知識、數學模型解決實際問題，幫助學生逐步形成一套完整的解題思路。這是培養學生數學建模素養的本質。因此，廣大數學教師在引導學生初步建立數學模型后，就需要教給學生利用模型解題的方法，其中數形結合思想乃是筆者在教學過程中最常采用的方法之一，也是利用模型解決問題最重要的方法之一。因此，為了進一步加深學生對數學模型的理解，在學生完成上述探究活動之后，還可以增設“探究變速自行車中的數學問題”活動，出示如下記錄單（表2）。

求解問題一：一個變速自行車有兩個前齒輪和6個后齒輪，能變化出多少種速度？從表中數據可以發現有兩個比的比值相等，所以6×2－1＝11（種）速度。

表2

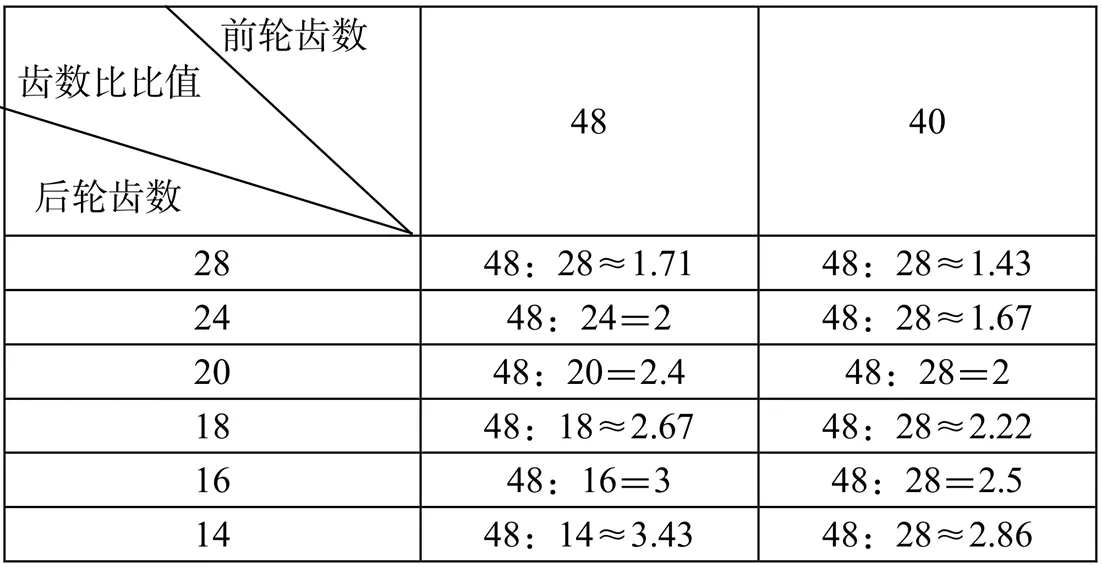
求解問題二：蹬同樣的圈數，哪種組合使自行車走得最遠？

教師先讓學生分析上述表單數據，然后鼓勵學生合作交流，最后師生共同總結結論：①前后齒輪齒數相差(比值)越大，后輪的轉動圈數就越多；②前、后齒輪齒數相差(比值)大的，比值就大，這種組合走得就遠；③前、后齒輪齒數相差(比值)少時，車速較慢。引導學生自己建立模型的基礎上，進一步解釋和驗證規律將變速自行車里的數學問題轉化為“比例”知識。

整個教學過程推進了數學模型的建立，讓學生在學習過程中了解了數學知識與生活的廣泛聯系，引導學生主動建立了普通自行車的速度與其內在結構關系的數學模型，幫助學生在“過程學習”中獲得了運用數學知識解決實際問題的思考方法——建立數學模型，也進一步加深了學生對所學知識的理解。

（三）加強拓展運用，提升學生建模素養

培養學生建模素養有利于提高學生數學知識應用能力。而從“教”之角度而言，數學建模其實是一種教學手段，但從學生“學”的角度而言，數學建模就是一種能力，一種學習策略，一種解決問題的技巧和方法。故此，要想通過數學教學培養學生建模素養，提高學生數學知識應用能力，數學教師還需要在教會學生建立模型和以模型解決問題之后，引導學生反復利用模型，并且將模型進行歸納整理，從而達到舉一反三、遷移運用的教學目的。同樣以《自行車里的數學》這一內容為例，在課堂接近尾聲時，不妨給學生來一個拓展延伸，設置如下當堂練習題：

習題1：一輛自行車的前齒輪齒數是32，后齒輪數是16，前后車輪的直徑為66cm，①請你算一算蹬一圈，自行車行駛多遠？②小明家和學校的距離大約有500米，如果蹬自行車上學，他要蹬多少圈？

習題2：一輛變速自行車的前齒輪數是2，分別有46和38個齒，后齒輪數是4，分別有20、16、14、12個齒，車輪的直徑66cm。自行車運動員在賽車時會經歷順風和爬坡兩種路段，請你為運動員在不同的路況下選擇前后齒輪。

聯系當堂教學內容設計習題，既可以幫助學生實現“堂堂清”，也能夠進一步引導學生運用數學模型解決實際問題，進一步促進學生數學模型思想發展，逐步提升學生數學建模素養。

三、結束語

綜上所述，學習知識的最終目的是運用知識解決問題，而解決大部分數學相關問題都涉及不同數學模型。廣大數學教師當重視學生建模能力培養，在課堂教學中充分給予學生探究活動空間，密切聯系學生實際生活，引導學生運用已有知識和生活經驗開展觀察、操作、推理等活動，讓學生真正感知數學模型，主動建立數學模型，應用數學模型，提高學生解決問題能力，促進學生核心素養發展。

[1] 李建卿.核心素養背景下初中數學滲透模型思想的策略[J].數學大世界(上旬),2019(08).

[2] 嚴蘇娟.以數學建模思想培養學生數學核心素養的教學實踐[J].考試周刊,2018(11).

[3] 沈國酰.將數學建模思想落到實處——以“解決問題的策略”為例[J].數學教學通訊,2017(01).

[4] 郭守貴.數學建模思想在小學數學教學中的應用分析[J].青海教育,2017(01).

[5] 王明會.在小學數學教學中融入數學建模思想的策略研究[J].天天愛科學(教育前沿),2021(05).

G622

A

1002-7661(2022)14-0150-03

本文系福建省科學“十三五”規劃2020年度課題《在小學數學教學中滲透模型思想的研究》課題成果，課題編號FJJKXB20-1045。