長程視野下數學起點型核心知識的遴選
【摘要】遴選起點型核心知識,比較高效的方法是運用抽象度分析法進行量化分析。通過繪制知識有向平面圖,借助三元指標來確定起點型核心知識,進而放眼全局,進行長程教學設計。
【關鍵詞】起點型核心知識;遴選方法;抽象度分析法;三元指標
【中圖分類號】G623.5【文獻標志碼】A【文章編號】1005-6009(2022)33-0015-03
【作者簡介】王俊亮,江蘇省揚州市江都區實驗小學(江蘇揚州,225200)教師,高級教師,揚州市數學學科帶頭人。
*本文系全國教育科學“十三五”規劃2020年度教育部重點課題“小學數學核心知識建構的教學研究”(DHA200370)階段性研究成果。
遴選起點型核心知識,比較高效的方法是運用徐利治和鄭毓信兩位教授在《數學抽象方法與抽象度分析法》一書中創建的抽象度分析法進行量化分析。
(一)抽象
抽象是指從具體事物中抽取出相對獨立的一個或幾個方面、屬性、關系等特質形成概念、公理、命題、關系、公式等“抽象物”的思維活動。在數學活動中,抽象更多地指向抽取數學概念、公理、命題、關系、公式等共同的、本質的特征形成新知識的思維活動。
(二)抽象關系
從概念、公理、命題、關系、公式中抽取出新知識形成的抽象關系有三種形式。
1.弱抽象。如果從原型A中選取某一特征或側面加以抽象,形成比A更一般的概念或理論B,使A成為B的特例,則A到B的抽象為弱抽象。如“正方形”弱化“四條邊相等”的特征為“對邊相等”就可以抽象出“長方形”,則從“正方形”到“長方形”的抽象為弱抽象。
2.強抽象。如果對于原型A,引入新特征強化得到概念或理論B,使B是A的特例,則A到B的抽象為強抽象。如“等腰三角形”強化“只有兩條邊相等”的特征為“三條邊都相等”就可以抽象出“等邊三角形”,則從“等腰三角形”到“等邊三角形”的抽象為強抽象。
3.廣義抽象。在概念或命題層面,如果定義概念B時用到了概念A,或證明命題B時用到了命題A,則B是A的廣義抽象。如證明“正n邊形的周長=邊長×n”時用到了“正n邊形的每條邊都相等”,則從“正n邊形的每條邊都相等”中推導出“正n邊形的周長=邊長×n”的抽象為廣義抽象。
(三)三元指標
依據知識點之間的弱抽象、強抽象或廣義抽象關系,把有關聯的知識點用單向箭頭連接(箭頭指向生發出的知識點)繪制成知識鏈,數條知識鏈相互勾連就形成知識結構網絡圖,我們稱之為知識有向平面圖(如圖1所示)。

1.出度和入度。“出度”和“入度”這兩個概念描述的是知識點之間一對多或多對一的抽象關系與程度。從一個知識結點x發出的有向線段的條數是它的出度,可以記為d出(x)。在圖1中,由于“因數”與“倍數”有著不可分割的相互依存關系,我們把它們看成一個知識點,從它們發出的線段條數是8,它們的出度可以記為:d出(因數與倍數)=8。同理,d出(公因數)=3,d出(公倍數)=2。指向一個知識結點x的有向線段的條數是它的入度,記為d入(x)。在圖1中,指向“最小公倍數”的線段是2條,“最小公倍數”的入度可以記為:d入(最小公倍數)=2。同理,d入(最大公因數)=2。
2.相對抽象度。相對抽象度描述的是知識點之間一對一的抽象關系與程度,它是指知識鏈上的知識點Cn相對于知識點C1的長度,可以記為:d相(Cn|C1)=n-1。如果連接C1與Cn之間的路徑有好幾條,則定義最大長度為相對抽象度。在圖1中,從知識點“因數”通向知識點“分解質因數”的路徑有3條,其中最長的一條知識鏈是:C1因數→C2質數→C3質因數→C4分解質因數,我們就定義在這個有向平面圖上,知識點“分解質因數”相對于知識點“因數”的相對抽象度為:d相(C分解質因數|C因數)=4-1=3。
出度、入度與相對抽象度合稱為三元指標。
(一)出度是判斷起點型核心知識的第一選擇
一個知識點的出度越大,說明它發出的有向連線就越多,意味著由它衍生出的新知識點就越多,它在這個知識結構體系中的基礎性就越強,就越有可能是起點型核心知識點。因此,繪制出知識有向平面圖,遴選起點型核心知識時,我們首先要分析知識點的出度。處于起始位置的知識點,如果在這個有向平面圖中的出度最大,一般是起點型核心知識點。如圖1中,作為這一組關聯知識的基礎知識,“因數與倍數”是一個核心知識,在這個有向平面圖中出度最大,又處在起始位置,它就是一個起點型核心知識。
(二)“出度+入度之和”是判斷起點型核心知識的第二個選擇
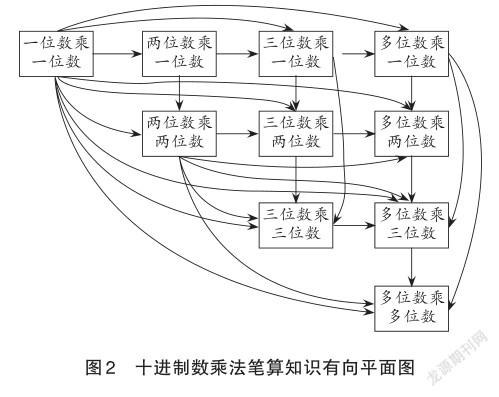
一個知識點的入度越大,指向它的有向連線就越多,意味著理解、運用這個知識點需要的支撐性知識點就越多,弄懂了這樣的知識點,就必然掌握了支撐它的這些知識及其之間的關系,顯然,它對于掌握知識結構體系很重要,因此,入度的數據體現了這個知識點的重要程度。當我們把它和“出度”結合起來時,“出度+入度之和”就成為遴選起點型核心知識的第二個選擇。起點型核心知識的主干位置,決定著它有時既要接受先出現的知識點的抽象關聯,有一定的入度,又要主動與其他知識點關聯起來,這使它又具有相對較大的出度。因此,在知識有向平面圖中,“出度+入度之和”最大或較大的知識點往往也是起點型核心知識。如圖2中,d出(兩位數乘兩位數)=5,d入(兩位數乘兩位數)=2,“兩位數乘兩位數”的“出度+入度之和”=5+2=7。除了“一位數乘一位數”之外,“兩位數乘兩位數”的“出度+入度之和”最大,因而它也是一個起點型核心知識。依據“出度+入度之和”判斷出的起點型核心知識常常具有開啟新的知識序列的特點。這里的“兩位數乘兩位數”就開啟了把多位數乘多位數的幾個積錯開分行羅列,再相加,最后求出計算結果的方法,是所有十進制數相乘的終極運算方法。
(三)相對抽象度是判斷起點型核心知識的第三選擇
在如圖3所示的鏈條式知識有向平面圖中,知識點之間的出度、入度基本均衡,很難用出度或“出度+入度之和”來判斷起點型核心知識。這時,我們可以用相對抽象度來遴選起點型核心知識。知識點Cn相對于C1的相對抽象度越大,表明知識點C1到達知識點Cn經過的弱抽象、強抽象或廣義抽象次數就越多,而知識點每經過一次抽象,深刻程度就會加深。因此,相對于末端知識點抽象度越大的知識點就越有可能是起點型核心知識。顯然,“自然數”作為整個數系的起點,經過一次次衍化,建構起一個數系,它是一個位于起始位置的起點型核心知識,其他知識都是借助自然數加上一些符號來表示的。
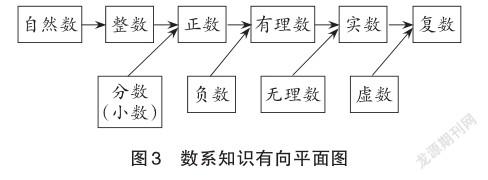
起于“自然數”的“數系”知識建構的長期性啟示我們,起點型核心知識的教學要立足長程視野,重視階段銜接與層級貫通,前面知識的學習一定要為后續知識預留好生長點與銜接口,促進后續知識的順利納入和自然生長。
[1]徐利治,鄭毓信.數學抽象方法與抽象度分析法[M].南京:江蘇教育出版社,1990.
[2]魏光明,王俊亮,劉正松,等.小學數學核心知識教學的理論與實踐[M].南京:江蘇鳳凰教育出版社,2020.
[3]王俊亮.小學數學核心知識教學中的抽象度分析[J].教育視界,2021(35):11-15.

