如何求解有關圓錐曲線中的焦點三角形問題
2022-07-13 21:54:34石小卉
語數外學習·高中版下旬 2022年5期
關鍵詞:解題
石小卉


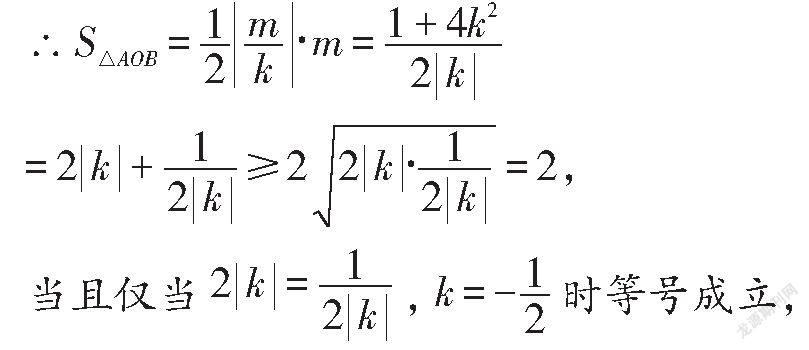
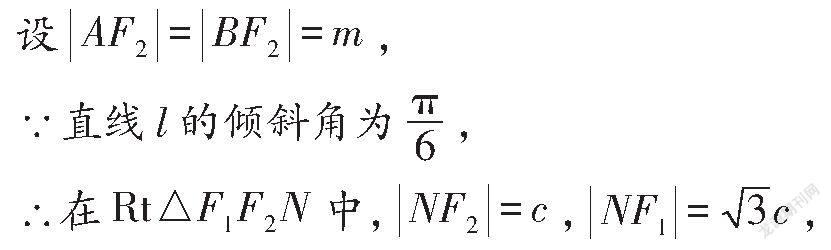
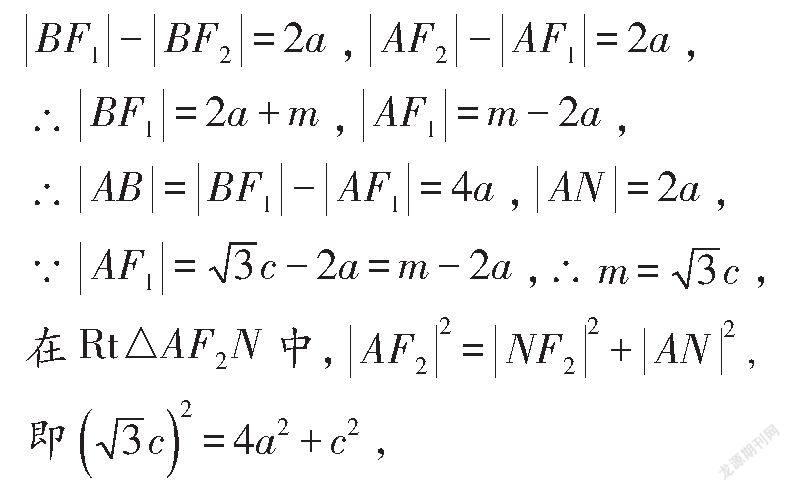


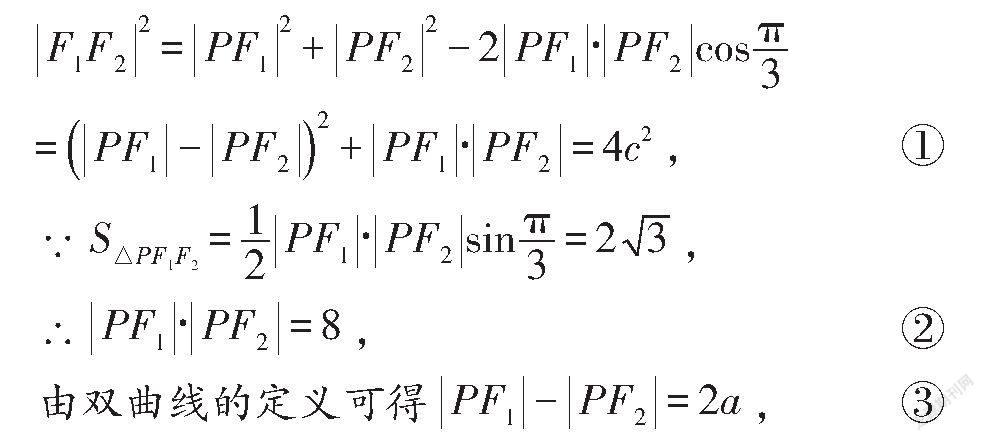
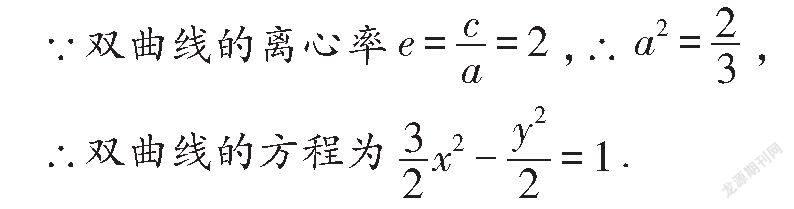

圓錐曲線的焦點三角形是指以圓錐曲線的焦點為頂點,且其他頂點在圓錐曲線上的三角形.有關圓錐曲線焦點三角形問題在解析幾何中比較常見,此類問題具有較強的綜合性,且計算量較大.有關圓錐曲線的焦點三角形問題主要有三種:離心率問題、曲線的方程問題、三角形面積問題.下面結合實例來探討一下這三類問題及其解法.
一、離心率問題
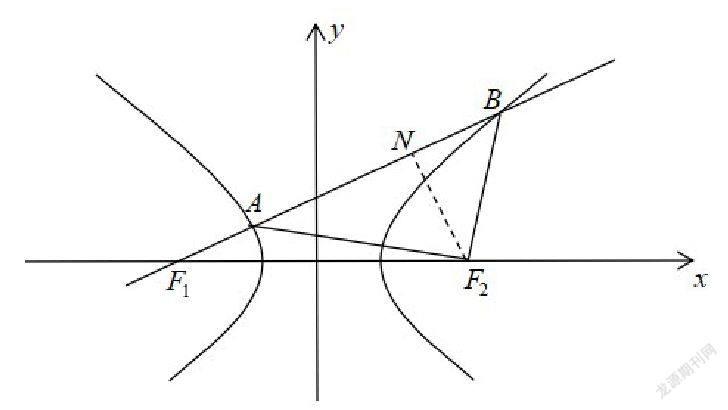
解:如圖,過點F作FN⊥AB交AB于點N,
由雙曲線定義可得,
二、曲線的方程問題
與圓錐曲線焦點三角形有關的曲線方程問題比較常見,一般要求動點的軌跡方程或者圓錐曲線的方程.解題的大致思路為:①設出圓錐曲線的方程或動點的坐標,②根據圓錐曲線的定義、焦點三角形的性質、三角形面積公式、余弦定理等,得到a、b的值,或與動點有關的式子,即可解題.
在△FPF中,由余弦定理可得
由①②③可得4c=4a+8,∴b=2,
解答本題,需先根據題意設出雙曲線的方程,然后根據雙曲線焦點三角形的特點、余弦定理、雙曲線的定義、三角形的面積公式建立關于a、c的關系式,求得雙曲線的方程.
三、三角形的面積問題
解答與圓錐曲線焦點三角形有關的面積問題,往往需根據圖形,明確焦點三角形的位置以及邊角關系,然后聯立過焦點的弦以及圓錐曲線的方程,得到一元二次方程,再利用韋達定理、弦長公式、三角形的面積公式求得三角形的面積或者取值范圍.
設直線l:y=kx+m,
化簡得(1+4k)x+8kmx+4(m-1)=0,
∴Δ=64km-16(m-1)(1+4k)=0,
∴1+4k=m,
∴△AOB的面積最小值為2.
解答與圓錐曲線焦點三角形有關的問題,要明確橢圓、雙曲線焦點三角形的特點,根據圓錐曲線的性質和定義建立焦點三角形三邊之間的聯系,構建關于a、c的關系式,這樣便能快速找到解題的突破口,順利解題.
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
中學數學雜志(2019年1期)2019-04-03 00:35:46
中學生數理化·中考版(2018年11期)2019-01-31 06:18:02
數學小靈通·3-4年級(2017年12期)2018-01-23 03:37:54
數理化解題研究(2017年4期)2017-05-04 04:07:56
讀寫算(下)(2016年11期)2016-05-04 03:44:22
中學生數理化·八年級數學人教版(2016年3期)2016-04-13 09:17:06
中學生數理化(高中版.高二數學)(2016年10期)2016-03-01 03:46:37

