判斷函數奇偶性常出現的錯誤以及規避的措施

王穎

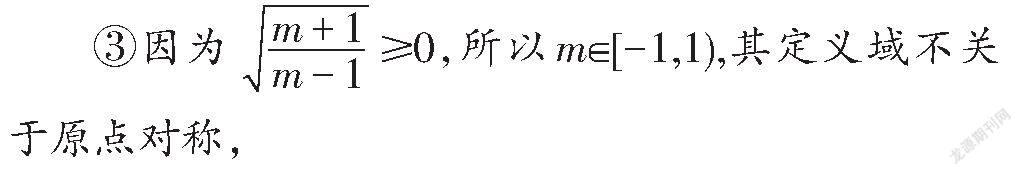
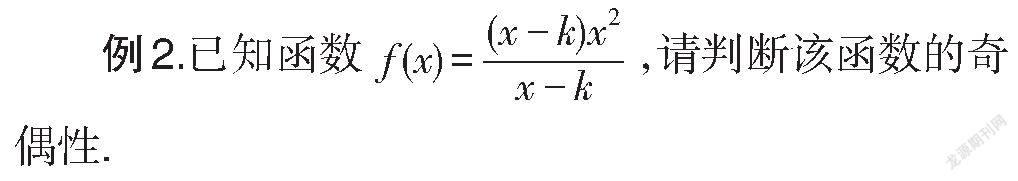
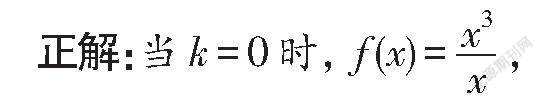
函數奇偶性是函數至關重要的性質之一.在判斷函數的奇偶性時，很多同學經常出現各種錯誤.對此，筆者就同學們在判斷函數奇偶性時常出現的錯誤進行了分析，并提出一些規避的措施，以期同學們能夠從中吸取教訓，避免重蹈覆轍.

錯誤之一：忽略了函數的定義域

函數的定義域是函數的三大要素之一，即函數自變量的取值范圍.在判斷函數的奇偶性時，很多同學常常忽略函數的定義域，致使解題出錯.

所以f（m）為偶函數;

上述解法之所以錯誤，是因為忽略了函數的定義域.事實上，具有奇偶性的函數的定義域都關于原點對稱，因此判斷函數的奇偶性，需先要判斷該函數的定義域是否關于原點對稱.

正解：①因為函數f（m）的定義域為{-1，1}其關于原點對稱，

又f（-x）=±f（x），所以該函數既是奇函數，又是偶函數;

所以f（m）既不是奇函數，也不是偶函數

所以f（m）既不是奇函數，也不是偶函數.

函數的定義域關于原點對稱是一個函數具有奇偶性的前提條件，所以在判斷函數的奇偶性時，同學們要高度重視函數的定義域，首先弄清楚函數的定義域是否關于原點對稱，若不關于原點對稱，則該函數不具有奇偶性.

錯誤之二：忽略了對參數的分類討論

在判斷含參函數的奇偶性時，需要對參數進行分類討論.然而受習慣性思維的影響，許多同學經常容易忽略對參數的分類討論，出現思慮不周的情況，致使求得的答案不完整，故而產生了錯解.

錯解：因為函數f（x）的定義域是（-∞，k）∪（k，+∞），其不關于原點對稱，所以函數f（x）既不是奇函數，也不是偶函數.

上述錯解產生的原因主要是受思維定式的影響，以為函數f（x）的定義域不關于原點對稱，故而沒有對參數k進行分類討論，導致解題出錯.事實上，當k=0時，該函數具有奇偶性.

該函數的定義域為（-∞，0）∪（0，+∞），

所以函數f（x）為偶函數;

當k≠0時，函數f（x）的定義域是（-∞，k）∪（k，+∞），其不關于原點對稱，

所以函數f（x）既不是奇函數，也不是偶函數.

在做題時，同學們要克服思維定式的影響，全面考慮問題，對可能出現的情況作全面分析，尤其要重視對參數的分類討論，從而做到不重復不遺漏任何情況，增加解答過程的完整性和準確性.在對參數進行分類討論時，可將實數R看作全集，根據函數的定義域或函數式有意義確定分類討論的分界線，將實數集劃分為幾個區間段，逐個進行討論，最后綜合所得的結果.

在判斷函數的奇偶性時，同學們務必要沉著冷靜，仔細審題，抓住函數式的特征，明確函數的定義域和參數對函數奇偶性的影響，根據函數奇偶性的定義進行判斷.同時要養成檢查和驗算的良好習慣，及時發現和糾正錯誤，從而確保解題無誤.