選擇合適的方法，求解曲線的方程問題

楊樓儉

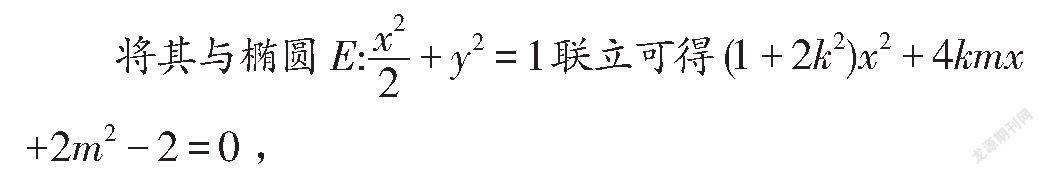
求曲線的方程問題在圓錐曲線中比較常見.此類問題側重于考查圓錐曲線的定義、幾何性質以及一元二次方程的性質.求解曲線的方程問題的方法有很多種，如定義法、相關點法、消參法、數形結合法等.那么，如何選擇合適的方法進行求解呢？下面結合實例加以說明.

一、定義法

運用定義法求解曲線的方程問題，主要是根據橢圓、雙曲線、拋物線、圓的定義來求解.這就要求同學們熟練掌握橢圓、雙曲線、拋物線、圓的定義，根據這些定義來建立關系式，求得曲線的方程.

∴4a=16-12，得a=l，

∵a+b=c=4，∴b3，

二、相關點法

有些求曲線的方程問題中的一個動點隨著另一個動點的變化而變化，此時可采用相關點法解題.首先設動點的坐標，并用該動點的坐標表示另外一個相關動點的坐標，然后將相關點的坐標代入滿足條件的方程中，即可得有關動點的軌跡方程.

解：由題意可得F（-2，0），F（2，0），設點A（x，y），B（x，y），M（x，y），

將兩式相減可得（x-4）（x-x）=（y-y）y，

得（x-6）-y=4，

當AB與x軸垂直時，點M（8，0）滿足（x-6）-y4，

∴點M的軌跡方程為（x-6）-y=4.

由題意可知，M點隨著A、B的變化而變化，因此可采用相關點法來解題.設出點A、B、M的坐標，并用M點的坐標表示出A、B，然后根據題意建立關于M點坐標的關系式，即可求出點M的軌跡方程.

三、消參法

消參法是解答圓錐曲線問題的重要方法.運用消參法求解曲線的方程問題，需先根據題意設出曲線上動點的坐標、動直線的方程、交點的坐標等，然后將其代入題設中，建立關系式，最后通過消參、化簡得到只含有動點的坐標的式子，即可求得曲線的方程.

解：①當切線l的斜率k存在且k≠0時，設直線l

的方程為y=kx+m，

∵動直線l與橢圓E只有一個交點，

∴Δ=16km-4（1+2k）（2m-2）=0，

整理可得m=2k+1，

∵直線MQ與直線l垂直，且經過M（l，0），

而m=2k+1，

∴點Q軌跡方程為x+y=2，

②當直線l斜率為0時，Q（l，±l）滿足x+y=2，

綜上所述，點。軌跡方程為x+y=2.

解答本題，需首先設出動直線的方程，將其與橢

圓的方程聯立，并消去y得到一元二次方程，根據直線與橢圓相切的關系可得Δ=0，據此得到關于參數、x、y的式子，通過消參求得Q點的軌跡方程.

相比較而言，定義法較為簡單;相關點法的適用

范圍較窄;消參法比較常用.在求解曲線的方程問題時，同學們可首先將問題與圓錐曲線的定義關聯起

來，運用定義法求解，然后分析動點之間的關系，合理選擇相關點法、消參法進行求解.