強(qiáng)GFP-內(nèi)射模的刻畫
◎吳雅麗
(廣東交通職業(yè)技術(shù)學(xué)院,廣東 廣州 510650)
文中的環(huán)都為結(jié)合環(huán)、且有單位元,所有的模都特指左模
內(nèi)射模是模與環(huán)范疇與同調(diào)代數(shù)理論的一種重要概念,它的研究方法與理論影響涉及代數(shù)和其他數(shù)學(xué)學(xué)科但是人們也看到了內(nèi)射模作為研究工具的局限性,因此產(chǎn)生很多關(guān)于內(nèi)射模概念的推廣2009年張力宏和劉巖運(yùn)用已知的-內(nèi)射模概念做出-內(nèi)射模的等價刻畫2013年,徐龍玉等人給出-投射模和-投射模是等價的與此同時,他們給出了-投射模對半單環(huán)的新刻畫
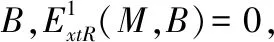
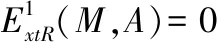
1 強(qiáng)GFP-內(nèi)射模
11若E為R-模給任意下圖模與同態(tài)的圖形:
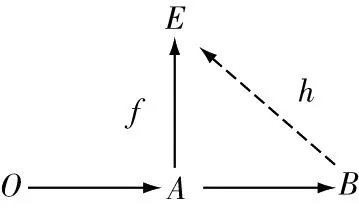
圖1
其中底行是正合的,模A是模B的任意有限表現(xiàn)子模,恒能完備為一個交換圖,即存在一個模同態(tài):→,使得=|,則稱模E是強(qiáng)GFP-內(nèi)射模
所以,內(nèi)射模也就是強(qiáng)GFP-內(nèi)射模在本文參考文獻(xiàn)已經(jīng)給了GFP-內(nèi)射模的等價刻畫,如果A為GFP-內(nèi)射模,當(dāng)且僅當(dāng)對任意自由模F的任何有限表現(xiàn)子模K,有限表現(xiàn)子模K到模A的同態(tài)均可以擴(kuò)張到自由模F到模A的同態(tài)由這個等價刻畫,可以得出結(jié)論:強(qiáng)GFP-內(nèi)射模為GFP-內(nèi)射模的一種
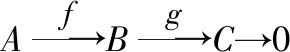
13若E為R-模,下列條件均為等價:
(1)E是強(qiáng)GFP-內(nèi)射模;
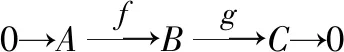
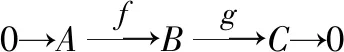
對任意的(,),因?yàn)镋是強(qiáng)GFP-內(nèi)射模,所以存在′∈(,),使得′=,即下圖可進(jìn)行交換:
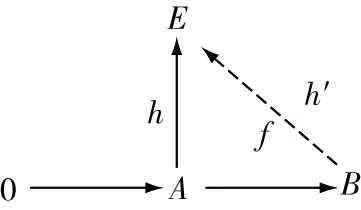
圖2
故(′)=′=從而是滿同態(tài),所以0→(,)→(,)→(,)→0是正合列
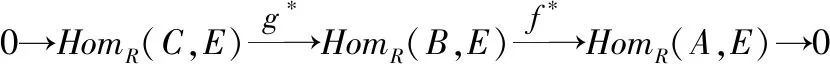
14如果模E是一個有限表現(xiàn)R-模,那么模E是強(qiáng)GFP-內(nèi)射模當(dāng)且僅當(dāng)任何形如0→→→→0分裂的

其次證明充分性對于正合列0→→及∈(,),A為有限表現(xiàn)R-模通過本文參考文獻(xiàn)[2] 253中定理可以得到充分性結(jié)論,下面兩行是正合列的交換圖:

圖3
通過證明,得出正合列0→→→∕→0是分裂的,即存在∈(,),使得=1令=,而===1=因此是強(qiáng)GFP-內(nèi)射模
結(jié)合本文參考文獻(xiàn)[2]中介紹的可除模定義,當(dāng)已知內(nèi)射模是可除模的一種時可通過證明得出結(jié)論:位于交換環(huán)上的任意強(qiáng)GFP-內(nèi)射模,都為可除模
15若R為交換環(huán),強(qiáng)GFP-內(nèi)射模都為可除模
當(dāng)模E為強(qiáng)GFP-內(nèi)射模,且S是R所有非零因子的乘法集時令∈,∈記=(),同時令()=則是一個同態(tài)因?yàn)槭且粋€非零因子,所以=()是一個自由主理想,從而是有限表現(xiàn)R-模因?yàn)槟是一個強(qiáng)GFP-內(nèi)射模,可推導(dǎo)出可擴(kuò)張為R到E的同態(tài)記作=(1),我們有=()=()=(1)=綜上所述模為可除模
與FP-投射模的情形類似,對于強(qiáng)GFP-內(nèi)射模方面也有下面對應(yīng)的定理
16([2]定理247)設(shè)下圖中行是正合列,圖中左邊的方圖可以進(jìn)行交換:

圖4
則存在:→′,使得右邊方圖成為交換圖
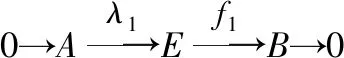
因?yàn)槟是一個有限表現(xiàn)R-模,模E是一個強(qiáng)GFP-內(nèi)射模,因此存在∈(′,),使得=通過引理16得到結(jié)論,存在∈(,),使得下圖可進(jìn)行交換:
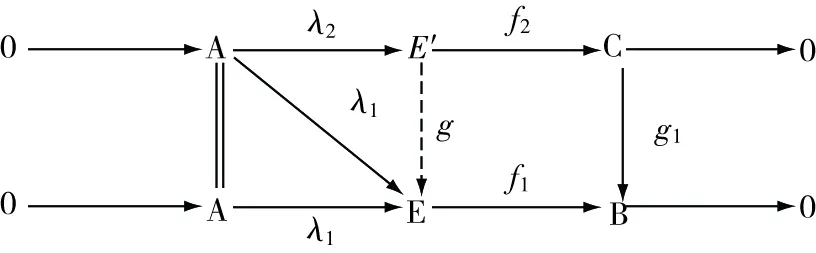
圖5

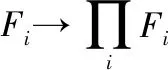
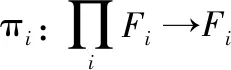
2 強(qiáng)GFP-內(nèi)射模對環(huán)的刻畫
下面來看一下強(qiáng)GFP-內(nèi)射模的等價刻畫
21若R為環(huán),下列條件都為等價:
(1)R是一個左G-半單環(huán);
(2)任意R-模都是一個強(qiáng)GFP-內(nèi)射模;
(3)強(qiáng)GFP-內(nèi)射模的子模就是強(qiáng)GFP-內(nèi)射模;
(4)任意一個有限表現(xiàn)R-模,其是內(nèi)射模
證明(2)?(3)任意強(qiáng)GFP-內(nèi)射模的子模是R-模,從(2)可知,任意強(qiáng)GFP-內(nèi)射模的子模,均為強(qiáng)GFP-內(nèi)射模
(3)?(2)對任意R-模C,C是其內(nèi)射包E(C)的子模,故C是強(qiáng)GFP-內(nèi)射模
(2)?(1)對任意R-模C,B是C的有限表現(xiàn)子模.由(2)知B是強(qiáng)GFP-內(nèi)射模,故對恒等映射1∈(,),存在∈(,),得出=1,其中:→是一個包含映射所以正合列0→→→→0是分裂的因此B是C的直和加項(xiàng)
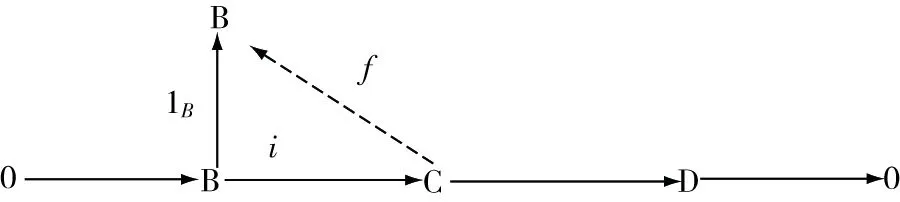
圖6
(1)?(4)設(shè)B為有限表現(xiàn)R-模,由于條件B是其內(nèi)射包E(B)的直和加項(xiàng),因此B是內(nèi)射模
(4)?(1)對任意R-模C以及其有限表現(xiàn)子模B,存在正合列0→→→∕→0,因?yàn)闂l件B是內(nèi)射模,所以該正合列分裂得到結(jié)論B是C的直和加項(xiàng)
當(dāng)R是一個左Noether環(huán)時,R是一個左G-半單環(huán)當(dāng)且僅當(dāng)R是一個半單環(huán)如果一個R-模M的任意子模都是它的直和加項(xiàng),可推導(dǎo)出M為半單模如果R自身的模為半單模,繼而R為半單環(huán).最終可以得出結(jié)論,當(dāng)且僅當(dāng)每個R-模都是內(nèi)射模或每個R-模都是投射模時,R為半單環(huán)
22若R為一個左Noether環(huán),下列條件都為等價:
(1)R是半單環(huán);
(2)任意的有限表現(xiàn)R-模都為內(nèi)射模
(1)?(2)顯然
(2)?(1)設(shè)I是R的左理想,因R是左Noether環(huán),所以I是有限生成的,因此I是有限表現(xiàn)模;因I為內(nèi)射模,可以得知正合列0→→→∕→0分裂從而可以推導(dǎo)出I是R的直和加項(xiàng),而R則是半單環(huán)
23([3]定理27)設(shè)R為左凝聚環(huán),下列條件均為等價:
(1)環(huán)R不僅為左自內(nèi)射環(huán),同時也為VN正則環(huán);
(2)環(huán)R為左G-半單環(huán);
(3)環(huán)R為左自內(nèi)射環(huán),且每一個R-模都為GFP-內(nèi)射模
由引理23可知,若為左凝聚環(huán),每個模都是強(qiáng)GFP-內(nèi)射模的條件為當(dāng)且僅當(dāng)是VN-正則環(huán)且是左自內(nèi)射環(huán)
 數(shù)學(xué)學(xué)習(xí)與研究2022年16期
數(shù)學(xué)學(xué)習(xí)與研究2022年16期
- 數(shù)學(xué)學(xué)習(xí)與研究的其它文章
- 利用電子白板提高小學(xué)數(shù)學(xué)課堂教學(xué)效率
- 小學(xué)數(shù)學(xué)教學(xué)與生活實(shí)踐結(jié)合的方法探究
- 教學(xué)法在中職數(shù)學(xué)教學(xué)中的應(yīng)用與探索
- 初中數(shù)學(xué)教學(xué)中學(xué)生數(shù)學(xué)思維的培養(yǎng)策略
- 初中數(shù)學(xué)函數(shù)教學(xué)存在的困難及教學(xué)對策
- 高中數(shù)學(xué)教學(xué)中學(xué)生數(shù)學(xué)思維能力的培養(yǎng)
