引導自主探究,深化建模思想
——以《17.1.3勾股定理在實際生活中的應用》教學設計為例
◎李幽蘭
(武漢市吳家山第二中學,湖北 武漢 430040)
數學源自生活,無處不在,數學在生活中的應用是非常廣泛的,很多問題都可以通過構建數學模型巧妙解決這就需要我們學會用數學的眼光看待生活中的事物,引導和鼓勵學生構建適當的數學模型,用所學的數學知識分析問題和解決問題,培養學生觀察、分析、思考、總結、協作的能力,讓學生體會數學知識的奇妙和學以致用的成就感勾股定理是數學中的一個重要定理,它是古代數學智慧的結晶,是用代數思想解決幾何問題的杰出代表下面以勾股定理在實際生活中的應用這一課的教學設計為例,探討構建數學模型在高效課堂中的應用
一、內容和內容解析
1內容:利用勾股定理進行簡單的計算,解決生活中的實際問題
2內容解析:勾股定理是最基本的數學定理之一,體現了直角三角形中三條邊之間的數量關系,它可用于解決直角三角形中的計算問題勾股定理在實際生活中具有廣泛的用途,本節通過聯系、比較、探索、歸納,幫助學生理解勾股定理,通過獨立思考與小組活動培養學生的分析能力和探究能力,以利于學生能夠正確地運用勾股定理解決實際問題
二、目標和目標解析
1目標:
(一)知識與技能:學生能說出勾股定理,能運用勾股定理的數學模型解決實際問題
(二)過程與方法:①通過從實際問題中抽象出直角三角形這一模型,深化“數形結合”和“轉化”的數學思想,將非直角三角形轉化為直角三角形,立體圖形轉化為平面圖形;②經歷探究勾股定理的應用過程,培養學生數學建模的意識,提高學生解決問題的能力;③運用分類討論的思想,讓學生更加全面地思考問題
(三)情感態度與價值觀:①數學源于生活,讓學生體會勾股定理在實際生活中的運用;②讓學生自主探索,團結協作,發揮學生的主觀能動性,培養學生不怕困難,積極自信的心理素質和思想品質;③讓學生熱愛校園,保護環境,加強環保意識和道德意識
2目標解析:
達成目標(一)的標志是:學生能夠運用勾股定理解決實際問題
達成目標(二)的標志是:學生知道怎樣將實際問題轉化為直角三角形模型
達成目標(三)的標志是:學生積極參與課堂學習,對數學學科的學習充滿信心和興趣
三、學情分析
在利用勾股定理探索實際問題的過程中,老師要讓學生經過思考克服困難,通過小組協作的形式實現高效課堂,提高學生的積極性和參與度,提高教學效率和教學效果讓學生在一堂課上不但收獲數學知識,還能從能力上、情感上、道德品質上都有收獲,促使每個學生都能得到相應的發展
本節課的教學重點:運用勾股定理解決實際問題
四、教學過程設計
(一)創設情境,導入新課
教師引言:數學源于生活,也服務于生活大家一起來看看這個問題能否用數學知識解決?
問題:如圖,學校有一塊長方形的花壇,有些同學為了走捷徑,就在花壇內的草坪上走出了一條“小路”,請你算一算,他們僅僅少走了________步路,卻踩壞了草坪(假設兩步為1米)

圖1
師生活動:讓學生回顧勾股定理的內容,并嘗試運用勾股定理解決這個問題教師在學生回答的基礎上明確提出解決問題的方法:同時指出這種方法就是構建直角三角形勾股定理的數學模型,將實際問題轉化為數學問題,從而運用勾股定理解決
根據勾股定理,

2×(3+4-5)=4(步)
因此,有的同學僅僅少走了4步路,卻踩壞了草坪
【設計意圖】讓學生回憶勾股定理的內容,并注意文字語言、圖形語言、符號語言的規范,初步體會通過建立數學模型解決實際問題,同時滲透 “兩點之間,線段最短”,為后續教學內容做鋪墊,也讓學生明白數學的價值不僅在于方便生活,更讓我們看清事物的本質,堅守道德與正義,呼吁大家要愛護校園環境
(二)新知構建,共研釋疑
1木板通過問題
1(人教版八年級數學下冊教材第25頁例1)一個門框的尺寸如圖所示,一塊長3 m,寬22 m的長方形薄木板能否從門框內通過?為什么?
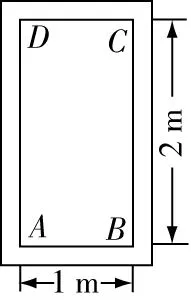
圖2
1木板橫著能否通過?
2木板豎著能否通過?
3在長方形中,,,哪條線段最長?
4門框能通過薄木板的最大寬度是多少?
學生帶著問題進行小組討論,通過小組組員協作演示,展示解題過程并講解,同時組員補充老師對學生的解題思路予以正面評價,但是關于運用勾股定理的書寫過程,老師要進行格式上的規范和強調
如圖所示,在Rt△中,根據勾股定理,
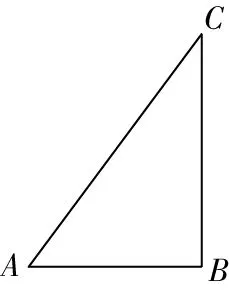
圖3
得=+=1+2=5,
所以木板可以從門框內通過
【設計意圖】讓學生能從實際生活的角度大膽考慮,用生活經驗和學過的數學知識加以思考和分析,最后能夠順其自然地想到將木板斜著通過門框,從而將這個實際問題轉化為解直角三角形的問題,成功構建了數學模型
2梯子滑動問題
2(人教版八年級數學下冊教材第25頁例1)如圖所示,一架26 m長的梯子斜靠在一豎直的墻上,這時為24 m如果梯子的頂端沿墻下滑05 m,那么梯子底端也外移05 m嗎?
分析問題:此題首先要計算梯子底端外移多少米,可以轉化為求的長度,而=-,自然想到要先利用勾股定理求、的長,老師引導學生完成這道題目然后用電子展臺將學生的解題過程展示出來,并給予正面評價,再次強調運用勾股定理的書面格式要規范
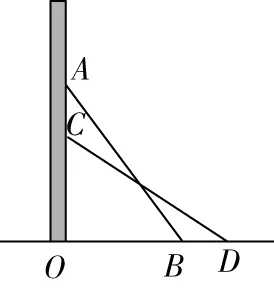
圖4
在Rt△中,根據勾股定理,
得=-=26-24=1,

在Rt△中,根據勾股定理,
得=-=26-(24-05)=315

∴=-≈177-1=077
所以梯子的頂端沿墻下滑05 m時,梯子底端并不是外移05 m,而是外移約077 m
【設計意圖】引導學生建立數學模型,分別畫出相應的直角三角形,明確已知量和所求量,再分析和轉化,提高學生分析問題、解決問題的能力
1一種盛飲料的圓柱形杯(如圖),測得內部底面半徑為25 cm,高為12 cm,吸管放進杯里,杯口外面至少要露出46 cm,求吸管至少要做多長

圖5
學生獨立思考完成變式練習,然后小組成員對各自的答案匯總和討論,由小組代表上臺充當小老師講題,其他小組成員可以對講解不清的地方發起提問,最后老師評價和補充
【設計意圖】鞏固訓練學生運用勾股定理在建立數學模型中解決問題的能力,培養學生自主探究、小組合作的學習能力,學習他人的長處,發現自己的不足,同時也站在教師的角度看待問題,更加全面和客觀地評價事物
(三)鞏固訓練,遷移拓展
3表面距離最短路徑問題
3如圖,一只螞蟻在棱長為的正方體表面爬行,它從頂點爬到頂點去尋找食物,則它走過的最短路程為( )

圖6
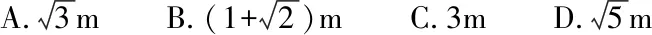
教師引導學生完成例題,總結解題方法
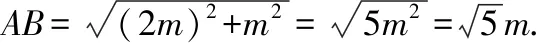
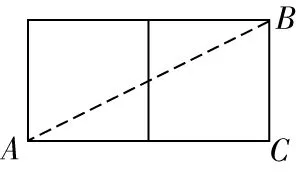
圖7
【設計意圖】對于平面圖形,由“兩點之間,線段最短”可以直接運用勾股定理求出兩點之間的距離,將立體圖形的側面展開,轉化為平面圖形,構造直角三角形,才能將實際問題轉化成可以用勾股定理計算的問題通過例題分析,建立數學模型,有利于幫助學生把握解題思路和技巧,促使學生學會歸納與總結方法
2有一個圓柱,它的底面半徑為3 cm,高為12 cm,在圓柱的底面點有一只蝸牛,它想從點爬到點,請問這只蝸牛沿著圓柱側面至少要爬行多少厘米
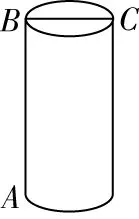
圖8
3長方體盒長、寬、高分別為5 cm,3 cm和8 cm,在盒子底端點有一只小蟲子,它想從盒子表面點爬行到點,那么小蟲子爬行的最短路程為________cm

圖9
師生活動:將學生小組分成兩部分,一部分做變式練習2,一部分做變式練習3,學生根據例題的方法,獨立思考完成變式練習,然后小組成員之間討論答案,以小組為單位展示解題過程(包含展開圖)并講解題目,進行小組比拼,然后老師點評和補充,同時提醒學生注意變式2只有一種情形,而變式3需要分類討論,考慮三種不同的展開圖情況,再來比較哪種路徑最短,并比較兩個變式練習與例3的聯系與區別對于小組比拼中表現優秀的學生和小組進行加分和全班鼓掌鼓勵,讓班級形成良性的競爭氛圍
【設計意圖】鞏固訓練學生解決立體圖形求表面最短距離的問題,討論答案和學生講解的過程讓學生在輸出的同時看到自己的不足,同時可以體會獲得成功的喜悅通過具體問題,深化運用勾股定理解決問題,通過學生的講題和小組之間的比拼,形成良性競爭,激發學生的集體榮譽感和比賽積極性
(四)課堂總結,反思升華
首先學生自由發言,表達自己本節課的收獲,然后教師概括并加以補充和升華

一節課的成功在于,教學目標明確,教學過程合理,學生積極參與、收獲知識并提高能力本節課的教學設計緊緊圍繞著構建直角三角形的勾股定理解決數學模型問題,以及怎樣構建數學模型,讓學生感受數學的生活氣息,激發學生學習數學的積極性本節課每個環節都充分體現了學生的主體地位,引導學生主動“自找水源”的學習意識;通過創設生活化情景,貼近學生的生活,達到最近發展區,深化數學建模思想;通過小組的組員之間、組與組之間、師生之間的課堂活動,形成互幫互助互補的師生學習共同體,更有利于形成良好的學習氛圍和學習習慣

