考慮不同固結階段條件下舊樁承載力的預測研究

蘇 聰 李鏡培 ，* 謝 峰

（1.同濟大學巖土及地下工程教育部重點實驗室，上海 200092；2.同濟大學地下建筑與工程系，上海 200092）

0 引 言

隨著社會經濟和城市建設快速發展，土地資源不斷減少，越來越多的建筑需要在已有建筑拆除后的場地上建設。舊樁再利用不僅能使再建建筑物減少材料耗費，而且可以節省在原址上二次施工費用[1]。但舊樁與新樁相比，不僅在自身材料與力學特性上有很大差別，其樁周土及環境因素等亦有區別，這些區別導致了舊有樁基與新樁在承載力計算方面有著很大不同。

靜壓樁沉樁產生的超孔隙水壓力會隨時間逐漸消散，土體的有效應力與強度也會逐漸恢復與提高[2]。因此，相較于新樁，舊樁周圍土體的力學特性發生了較大的變化，而在超孔隙水壓力消散之后，土體還會發生以土體蠕變為主的次固結，這一過程也會造成土體孔隙比下降、強度與承載力增加，上述過程就是樁基承載力的時效性。

對于樁基承載力變化的計算可以分為理論解析解法和經驗公式方法，這兩種方法有著各自的優缺點。

首先是理論解析解，關于舊樁樁周土體的力學特性，Li等[2]基于K0-MCC修正劍橋模型以及圓孔擴張理論推導出了樁周土體應力以及孔壓解答，該解答也被李林[3]用于推導靜壓樁時變承載力與沉樁終壓力的理論關系。上述理論解析方法雖然可以解釋承載力的變化機理，但是計算過程過于復雜，不便運用于工程實際中，同時理論解析解大多考慮的是沉樁結束后超孔隙水壓力消散的主固結階段，無法反映次固結階段樁基承載力的變化。

在樁基承載力變化的經驗公式解答方面，Skove和 Denver[4]、Tan 等[5]通過實測數據提出了基于短期承載力估算長期承載力的經驗公式。但經驗公式的準確性依賴于場地條件等諸多因素并且不能反映承載力變化的內在機理。

Komurka[6]通過總結大量試驗數據，認為黏土中沉樁完成后，樁基承載力隨時間的變化規律可大致分為三個階段：第一階段，在沉樁結束后較短的時間內，承載力增長幅度與時間對數呈對數關系；第二階段，承載力增長幅度與時間對數呈近似直線關系；第三階段，沉樁產生的超孔壓基本消散，土體結構性變化、蠕變等效應引起樁承載力緩慢變化，其增長幅度與時間對數呈線性關系，該階段即為次固結階段。

關于次固結階段樁基承載力的變化，尹振宇等[7]總結了軟黏土蠕變研究的現狀，討論了一維、三軸、復雜應力條件下軟土蠕變的特性。Liingaard等[8]提到了Bjerrum的經典時間等值線模型，認為在e-lgp坐標下不同時間的變形線是一系列相互平行的直線，即孔隙比隨時間的變化與土體原應力狀態無關。

針對上述研究中存在的問題，本文主要對舊樁承載力的時效性及其簡化計算方法進行討論。首先以承載力增長的機理不同將承載力的變化劃分為主固結與次固結兩個不同的階段，并提出了可應用于工程實際的簡化計算公式；最后通過奧西拉河試樁試驗的數據，驗證了本文簡化計算理論的有效性。

1 主固結階段承載力時效性

本文提出使用時效性系數來表現沉樁結束之后承載力的變化，定義時效性系數βt為沉樁后任意時刻樁基承載力與初始時刻承載力標準值的比值：

該定義下，任意時刻的樁基承載力Qt可以表示為

式中，承載力時效性系數βt采用本文提出的簡化公式進行計算，對于不同的固結階段，由于引起樁基承載力增加的主要機理不同，βt將采用不同的簡化方法進行計算；Q0表示t0時刻承載力標準值，可以參考規范中的經驗參數法以及靜載試驗法確定；Qt表示t時刻的樁基承載力。

1.1 主固結階段承載力時效性的計算

對于主固結階段承載力的時效性，已經有不少國內外學者進行過相關研究，相關研究主要可以分為經驗公式法以及理論解析解法。

1.1.1 經驗公式

關于主固結階段樁基承載力時效性，最經典的經驗公式是Skov和Denver[4]提出的半對數經驗公式。Haque等[9]對靜壓樁時效性經驗公式進行了總結，如表1所示。

表1 樁基承載力時效性經驗公式（部分）[9]Table 1 Empirical calculation formula of time-dependent bearing capacity of driven pile（Part）[9]

以上經驗公式雖然與實測數據有很好的吻合度，但也存在一些缺點：①經驗公式是否準確在很大程度上依賴于試驗場地的地質條件、施工方法及樁型；②經驗公式忽略了靜壓樁承載力時效性的內在機理，無法反映靜壓樁承載力隨時間變化的本質。

1.1.2 承載力與超孔隙水壓力解析解

關于承載力時效性的理論推導，大部分研究結果以及實測數據都表明，主固結階段承載力的時效性主要與超孔隙水壓力的消散有關。李林等[3]基于圓孔擴張理論推導出的承載力時效性公式表明，樁側與樁端阻力隨時間的變化都與樁側水平向有效應力的變化成正比，但是其關于孔隙水壓力消散的解析解為無窮級數的形式，求解較為復雜，難以運用于工程實際計算中。

對于初始超孔隙水壓力，本文采用的是南京工業大學宰金珉等[10]提出的計算公式，該公式不僅簡潔，同時反映了超孔隙水壓力在徑向和沿深度方向的變化規律，克服了超孔隙水壓力計算值在邊界上的不連續，且計算結果與實測結果基本一致，其表達式為

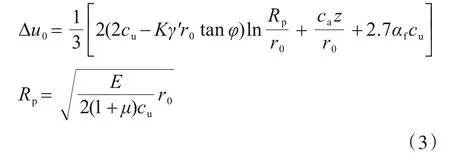
式中：Δu0為初始超孔隙水壓力；Rp為塑性區半徑；cu為土的不排水抗剪強度，K=tan2(45°+φ/2)，φ、ca為樁土界面的摩擦角、黏聚力；γ'為土體浮重度；r0為樁的半徑；z為計算點的深度，αf=0.707(3Af-1)；Af為孔壓系數；μ為土的泊松比；E為土體彈性模量。

1.2 經驗公式參數擬合

Skove 和 Denver[4]通過實測數據提出了基于短期承載力估算長期承載力的經驗公式Qt=Q0[Alg(t)+1]，但該經驗公式中經驗參數A的取值無法反應不同場地條件的差異性，因此本文對經驗參數A的取值進行擬合，以提供更加精確的參數取值方法。宰金珉等[10]認為超孔隙水壓力消散快慢主要與土體的水平向固結系數Ch以及樁徑r0有關，Ng等[11]提出樁基承載力的變化與無量綱時間因子成正比。而主固結階段樁基承載力的變化過程就是超孔隙水壓力的消散過程，因此對于經驗公式，參數A應當與水平向固結系數Ch以及樁徑r0有關。所以假設經驗參數是固結系數Ch以及樁徑r0的函數。

本文選取了三個實例，分別來自于宰金珉等[10]，李林等[3]的試驗結果。根據本文定義，承載力時效系數，將三個實例的承載力時效系數隨時間的變化繪制在對數坐標系中，如圖1所示。

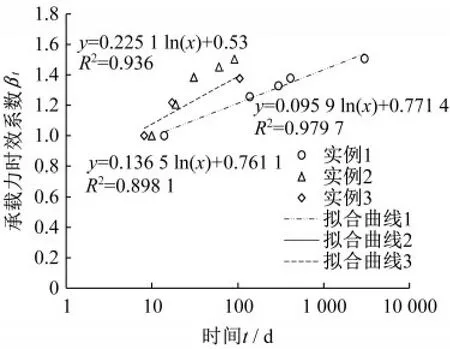
圖1 實例擬合曲線（對數坐標）Fig.1 Fitting curve of examples（logarithmic coordinates）

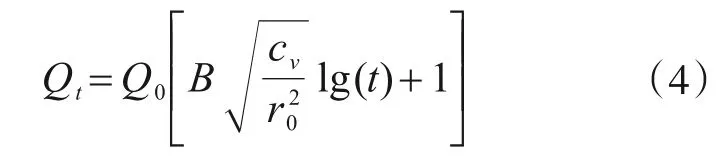
式中，B為經驗參數，根據實例數據擬合結果，參數B取值為0.4。

1.3 半理論半經驗簡化公式

根據李林等[3]的研究，任意時刻樁基承載力與初始時刻樁基承載力之比等于任意時刻樁基徑向有效應力與初始時刻樁基徑向有效應力之比：

以下計算過程中，對于初始超孔隙水壓力Δu0采用南京工業大學的理論解。對于超孔隙水壓力的消散過程，為便于工程實際的應用，采用經驗公式擬合方法，簡化為對數衰減過程。

擠壓力的求解參考姚笑青等[12]的計算方法：

ur·Af=Δu0，初始擠壓力，則t時刻土側向有效應力：

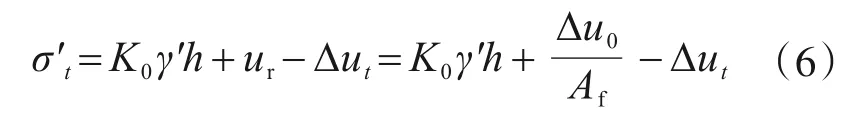
Δut的簡化計算公式為

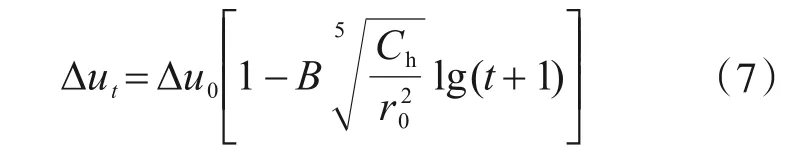
式中，B為經驗參數，根據2.2節實例數據擬合結果取0.4。

在1.2節選取的三個實例中，通過半經驗半理論公式計算得出的承載力時效系數與實測結果的對比如圖2—圖4所示。

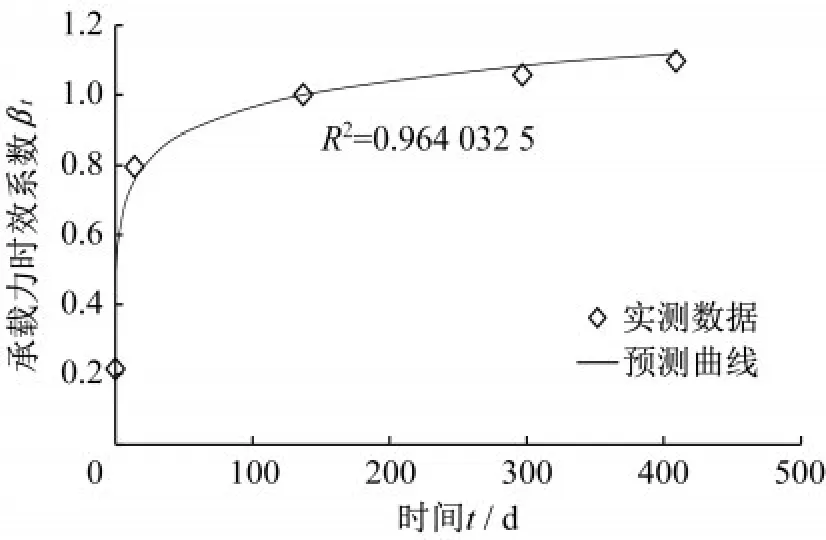
圖2 實例一實測數據與預測曲線對比Fig.2 Comparison of measured data and predicted curve for example 1

圖3 實例二實測數據與預測曲線對比Fig.3 Comparison of measured data and predicted curve for example 2

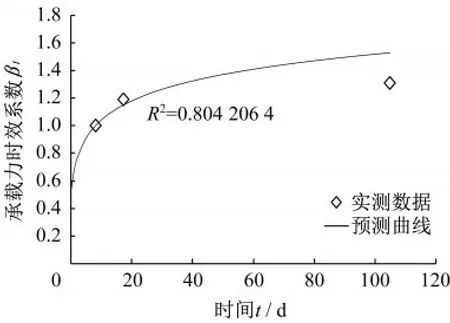
圖4 實例三實測數據與預測曲線對比Fig.4 Comparison of measured data and predicted curve for example 3

采用統計學中的決定系數R2對本節提出的半經驗半理論公式的計算結果進行評價。決定系數R2又稱測定系數、可決系數，是回歸分析中說明因變量變化可靠程度的一個統計指標，其定義為

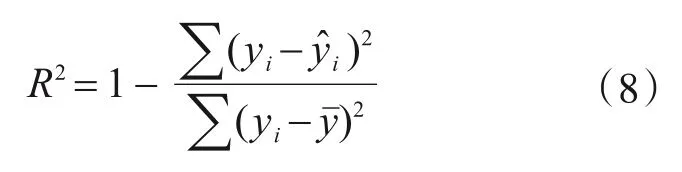
式中：yi為實測數據值為回歸數據值為實測數據平均值。

為了避免出現負值，對簡化公式進行線性變換，等效成為線性回歸的形式，計算得出簡化計算公式的線性回歸R2值如表2所示。

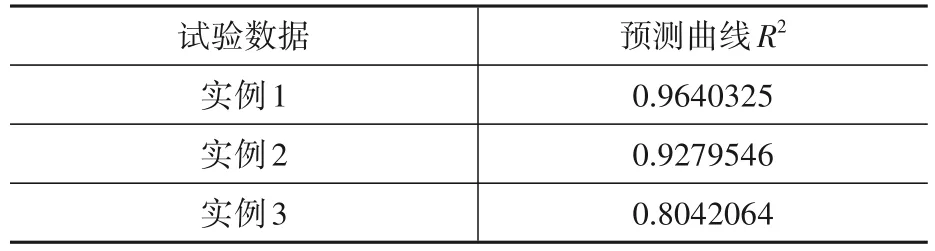
表2 線性回歸R2計算值Table 2 The coefficient of determination R2after linear regression

從表2計算結果可以看出，預測曲線線性回歸后的相關決定系數均達到了0.8以上，決定系數越接近1，表明回歸效果越好，本節提出的半理論半經驗公式能夠很好地反映實際承載力隨時間的變化。

2 次固結階段承載力時效性的計算

2.1 次固結階段研究的重要性

眾多研究與工程實例表明，沉樁完成后，樁周土的超孔隙水壓力大多會在一個月內基本消散完畢，雷華陽等[13]在天津東疆保稅港區二期工程中選取的實測結果表明，沉樁后20 d，絕大部分土層超孔隙水壓力消散率在90%以上。Konrad等[14]也指出樁周土的超孔隙水壓力在33 d左右完全消散，Roy等[15]指出超孔隙水壓力的消散時間為20 d左右。

因此在討論沉樁結束后樁基較長時間內的承載力變化時，對次固結階段樁基承載力變化的計算也尤為重要。次固結階段樁周土體中超孔隙水壓力已基本消散完畢，土體強度變化主要由土顆粒蠕變引起，因此對次固結階段樁基承載力的時效性計算將重點研究土體的孔隙比變化。

2.2 次固結階段承載力時效系數簡化計算公式

次固結階段土體的變形主要由土顆粒蠕變引起。許多室內試驗和現場量測的結果都表明，次固結程度大小隨時間的變化在半對數坐標系上接近于一條直線。Liingaard等[8]按照Bjerrum的經典時間等值線模型給出了孔隙比隨時間變化的表達式，如圖5所示，從圖中的時間等值線中可以看出，e-lgp坐標下不同時間的變形線是一系列相互平行的直線，意味著孔隙比的變化Δe與初始應力狀態p0無關。

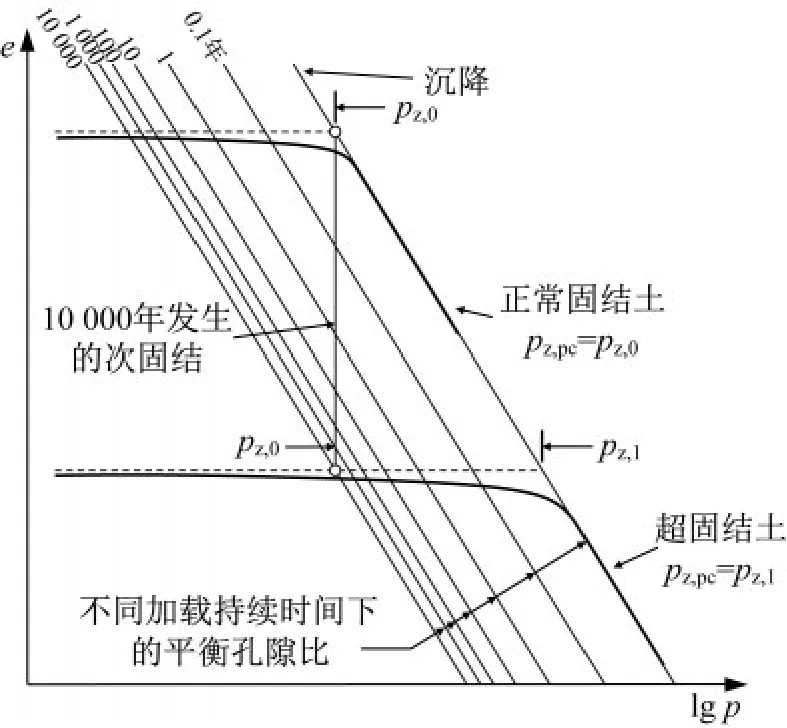
圖5 時間等值線模型Fig.5 Bjerrum’s time contour model

Bjerrum經典理論[8]考慮的是一維固結下孔隙比的變化，其表達式為

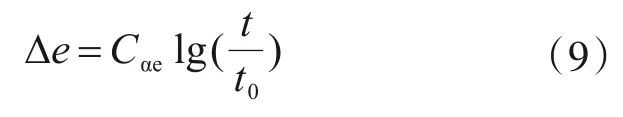
式中，Cαe為次固結系數，與土體本身的應力狀態有關。

2.3 次固結階段簡化公式實例驗證

為驗證簡化式（12）的準確性，將簡化公式計算結果與Augustesen等[16]實測數據中16.1號試樁的實測結果對比如圖6所示。

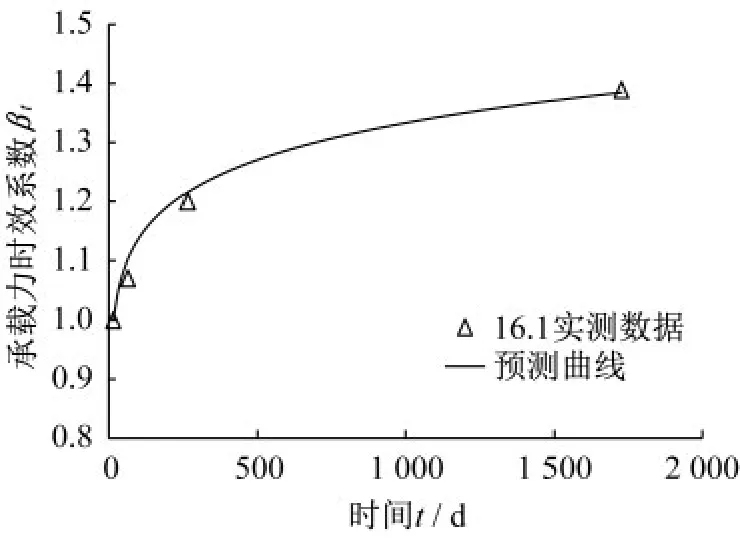
圖6 實例16.1與預測曲線對比Fig.6 Comparison of measured data and predicted curve for example 16.1

從圖6中可以看出，簡化公式計算出的預測曲線與實測值之間有令人滿意的吻合程度

簡化公式中參數λ和κ的值比較固定，變動范圍不大，對承載力時效系數計算結果的影響較小。2.4節將對次固結系數Cαe、初始時間t0對于簡化公式（13）計算結果的影響進行討論。

2.4 次固結階簡化計算公式參數分析

2.4.1 次固結系數

土體的次固結系數主要與土體的應力狀態有關，但并不是簡單的線性關系。胡建平等[17]對浙江平陽港區近海黏土的次固結系數進行了研究，圖7為同一鉆孔不同深度次固結系數與土體應力大小的關系。

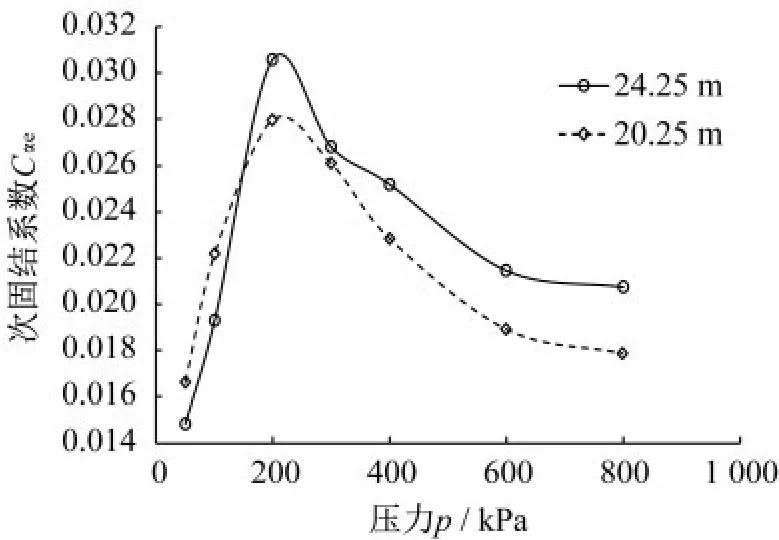
圖7 不同深度處次固結系數與壓力的關系（浙江沿海）Fig.7 Relationship between secondary consolidation coefficient and pressure at different depths（coastal area of Zhejiang Province）

從圖7中可以看出，次固結系數的范圍在0.01～0.07之間。結合其他相關文獻研究成果，次固結系數大多在0.005～0.03的區間內。本文以0.004 為梯度，分別取Cαe=0.014，0.018，0.022，0.026，0.030，0.034，計算并繪出不同次固結系數下承載力時效系數βt與時間t之間的對數關系，如圖8所示。

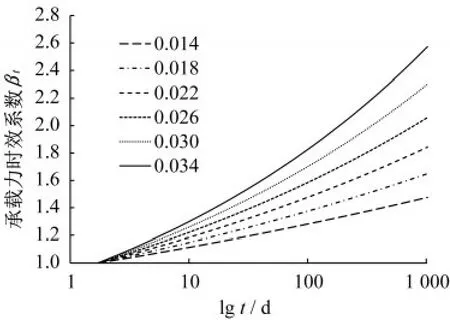
圖8 承載力變化趨勢隨次固結系數的變化Fig.8 Trend of bearing capacity with secondary consolidation coefficient

從圖8中可以看出次固結系數對于承載力時效系數βt的影響：次固結系數Cαe越大，βt-lgt曲線的斜率就越大，承載力時效系數隨時間增長就越快。

結合圖7以及圖8的計算結果可知：當土體應力小于200 kPa時，隨著土體應力增加，次固結系數增加，承載力時效系數隨時間增長越快；當土體應力大于200 kPa時，隨著土體應力增加，次固結系數減小，承載力時效系數隨時間增長越慢。

2.4.2 初始時刻

為了進一步探究初始時刻t0選取對承載力時效系數計算的影響，在式（12）的基礎上，加入時間調整系數Ψ來考慮初始時間的影響，修改后的公式：

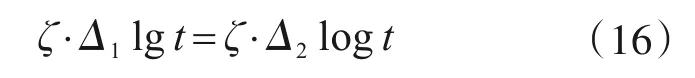
即Δ1=Δ2?Ψ1=Ψ2，說明對于簡化式（12），無須根據初始時刻選取的不同而對公式進行調整，初始Q0，t0取任意值，計算出的Qt都是一樣的。因此，雖然初始時刻t0的取值不同會影響承載力增長比例βt的計算結果，但是不會影響最終計算的任意時刻承載力Qt的計算結果。

3 實例計算

本節將主固結和次固結階段的簡化計算公式結合，對樁基沉樁結束后較長時間內的承載力變化進行預測。選取Bullock等[18]在奧西拉河試樁的實測試驗結果作為對比。奧西拉河試樁的試驗周期跨度較長，實測數據從第0.98 d到1 727 d（4.73年），可以較好地反映樁基從主固結階段到次固結階段全過程的承載力變化。

使用簡化公式對奧西拉河試樁主固結階段樁基承載力時效系數進行計算時，土體參數參考第二節中的黏土參數，計算得出超孔隙水壓力在91 d左右消散完畢，91 d之后的承載力時效系數使用第三節次固結階段的簡化公式進行計算，取t0=91。將第0.98 d時的承載力作為樁基承載力標準值，計算試樁各個時間點的承載力時效性系數，與簡化公式計算結果對比如圖9所示。

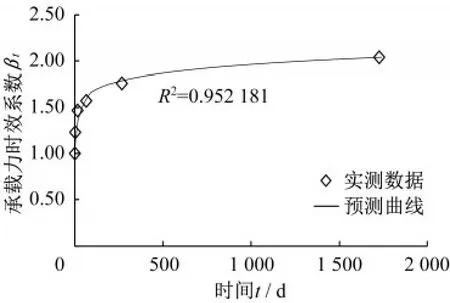
圖9 奧西拉河試樁實測數據與預測曲線對比Fig.9 Comparison of measured data and predicted curve for the test pile in the Osceola River

從圖9中可以看出，在t=0.98 d、2.97 d、16.1 d、65.1 d、265 d和1 727 d時，承載力時效系數βt分別為1、1.23、1.47、1.57、1.76和2.04，承載力分別為972 kN、1 197 kN、1 427 kN、1 528 kN、1 712 kN和1 982 kN，采用本文提出的簡化公式計算得到的承載力時效系數預測值βt分別為1、1.11、1.34、1.59、1.79和2.04，承載力預測值分別為972 kN、1 080.26 kN、1 299.19 kN、1 545.23 kN、1 739 kN和1 981.28 kN，實例結果與預測公式的決定系數R2=0.952 181，非常接近1，表明用本文提出的簡化計算方法對樁基承載力時效性進行預測有較好的吻合程度。

4 結論

（1）本文定義了承載力時效系數βt來計算承載力隨時間的變化。根據已有研究成果將樁基承載力隨時間的增長劃分為主固結與次固結兩個階段。

（2）考慮主固結階段承載力的變化主要由超孔隙水壓力的消散引起。提出了將解析解與經驗公式模擬消散過程相結合的半經驗半理論簡化計算公式，用R2對公式的擬合精度進行了初步評價。

（3）考慮次固結階段承載力變化主要由土體蠕變引起，采用了經典的一維固結理論對次固結階段孔隙比的變化進行模擬，得到了次固結階段承載力的簡化計算公式，綜合相關文獻試驗的實測數據對公式進行了驗證。

（4）本文利用奧西拉河的試樁數據進行驗證，將主固結與次固結階段的預測公式結合在一起，進行了承載力長周期變化的計算。對比結果表明本文提出的承載力變化簡化計算公式可以比較合理地預測長期受荷樁的承載力變化，對工程實際中的計算有一定的參考價值。