京杭運河航運與沿河區域經濟的互動關系研究

陳乾陽，董思遠，朱小磊

(山東省交通規劃設計院，山東 濟南 250031)

我國經濟進入高質量發展階段，國家“十四五”規劃綱要提出采用擴大內需和產業升級的手段，推動城市群協調發展。產業升級和城市群發展過程中的資源要素配置誘發了貨物運輸需求[1]。內河航運作為中間產品型基礎產業，對沿河區域國民經濟發展和產業優化升級有著較大的拉動作用與輻射效應，影響沿河區域經濟和產業結構的協調發展[2-3]。京杭運河是我國唯一貫穿南北的縱向航道，途經京津冀、長三角等國家級城市群，其黃河以北段復航工作逐步列入沿線區域航運建設日程。在我國經濟高質量發展階段，如何規劃沿河區域產業布局，調整產業結構，充分發揮航運資源優勢，釋放沿河區域經濟發展潛力，是京杭運河黃河以北段復航工作亟待解決的問題之一。

鑒于京杭運河黃河以北段未復航，無法直接探尋該段與沿河區域經濟的互動關系，因此本文擬以京杭運河通航的某一航段為例進行研究。為了增強研究結果的可借鑒性，需要該航段沿河區域經濟與黃河以北段沿河區域經濟地位高度相似，且航道等級高。蘇北運河從北向南依次跨越徐州、宿遷、淮安和揚州，是全國除長江以外等級最高、綜合效益最好的干線航道，常年有13省市的船舶通過，承擔著北煤南運和長三角地區大宗貨物集散的重要任務。因此，本文選取京杭運河蘇北段及沿河腹地為研究對象，研究京杭運河航運與沿河區域經濟的互動關系，并選擇徐州某產業園作為微觀分析案例，提出對京杭運河黃河以北段沿河區域產業布局規劃具有應用價值的建議。

當前內河航運與沿河區域經濟互動關系的研究主要有內河航運與經濟互動關系的評價以及內河航運對經濟貢獻度的測算等。許長新[4]定義了港航經濟系統，將港航、水運、工程經濟以經濟學的思想有機地聯系在一起，為后續學者研究內河航運與沿河區域經濟發展提供了借鑒。學者多選擇重慶市[5]、湖北省、浙江省和江蘇省等內河航運相對發達的省域作為研究區域，研究結果多為正向關系。王凱文等[6]認為湖北省內河航運與區域經濟發展存在長期穩定關系，兩者相互促進，互為因果。王雅等[7]進一步計算了湖北省內河航運發展對該省國民經濟的貢獻率，結果顯著為正。相比之下，四川省內河航運有著更大的發展空間，具備與區域經濟進一步相互協調、相互促進、共同提高的基礎條件[8]。湯東建等[9]研究發現區域經濟和工業發展對江蘇省內河航運有顯著的促進作用，而后者對前者的促進作用不明顯。靖學青[10]將長江經濟帶分為東部地區和中西部地區兩個區塊分別進行實證分析后發現，水運對經濟增長起到顯著正面作用的只是長江東部地區，究其原因，該地區除沿江運輸外還包括了海洋運輸。顧婧瑜[11]構建了定量模型反映長江深水航道建設對區域經濟的促進作用。此外，還有部分學者直接就航運業對區域社會的經濟貢獻進行了測算[12]。吳曉磊等[13]以京杭運河黃河以北段為例，提出了內河航運對區域經濟貢獻的定量計算方法。

在內河航運與沿河區域經濟發展的演化過程中，各主體通過制度性與非制度性的安排，將資源和功能進行緊密結合，不斷追求利益最大化，從而使得航運、產業、區域經濟三者的協調程度不斷變化。如今，內河航運在發揮裝卸、轉運等基礎功能外，還推動了資金、人才、信息等要素的集聚，促進了關聯產業的發展，提升了沿河區域的經濟活力；同時，區域經濟為內河航運提供了貨源，總體形成了良性循環發展。內河航運與沿河區域發展內部結構作用機理如圖1所示。

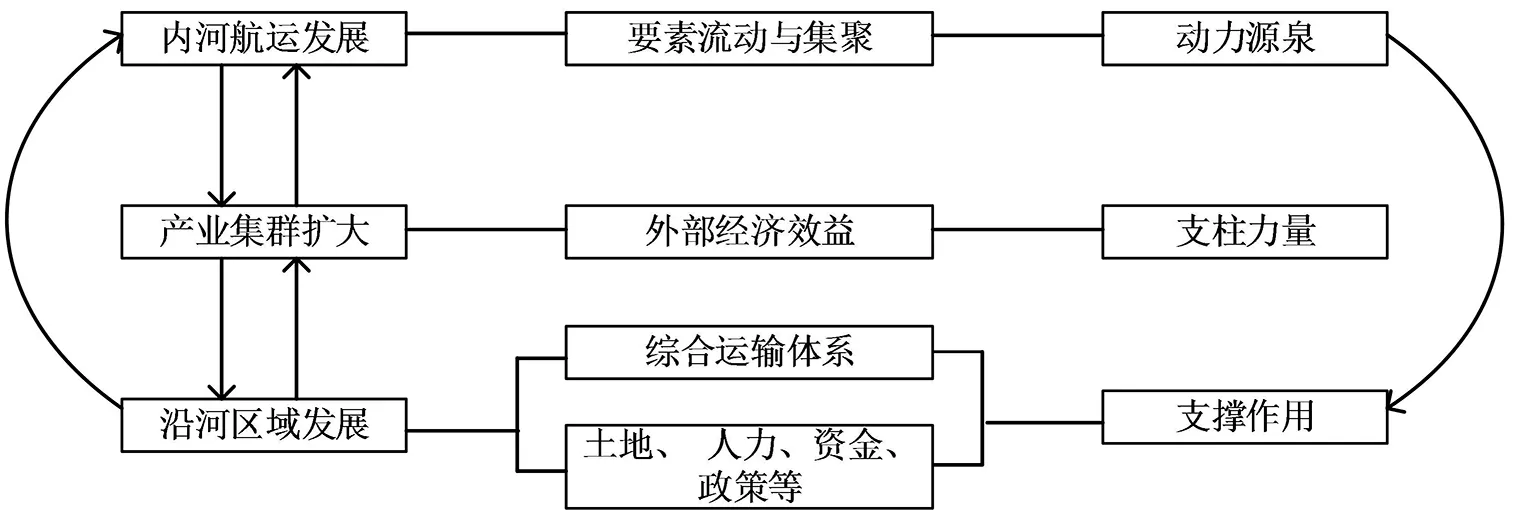
圖1 內河航運與沿河區域經濟互動發展的作用機理Fig.1 Interaction mechanism between inland waterfront shipping and the waterfront regional economy

本文在測算蘇北運河發展與沿河區域經濟和三次產業灰色關聯度的基礎上，通過協同性分析，探尋蘇北運河航運與沿河區域經濟和產業結構的互動變化規律，刻畫蘇北運河對沿河區域經濟的影響和作用，為京杭運河黃河以北段復航工程設計、復航河段沿河區域產業布局規劃和城市群建設提供借鑒。

1 蘇北運河航運與區域經濟關聯度

內河航運在不同區域有著不同的發展，與區域經濟發展的互動關系研究結果各異。京杭運河黃河以北段沿河4個省市中，北京市無1979—2019年水運貨運量數據，山東、河北和天津研究結果都顯示水運未與區域經濟發展形成長期均衡關系，航運發展有進一步提升的空間。鑒于交通運輸方式選擇對地理特征與交通體系優勢的敏感性，研究對象選擇沿河區域并縮小地理范圍。此外，省級水運貨運量數據不僅包含內河航運貨運量數據，還包括了海運貨運量，為排除海運貨運量對研究結果的影響[10]，本文選取蘇北運河水運貨運量數據。由于蘇北運河沿河經濟帶涉及的縣、區較多，相關數據口徑不一致，數據難以收集，故本研究選取蘇北運河沿河經濟帶主要城市宿遷、徐州、淮安和揚州。

1.1 變量選取和數據來源

水運貨運量指標選擇1991—2018年蘇北運河10個船閘貨物通過量總和T(噸)，反映蘇北運河航運發展狀況和總體趨勢，船閘貨物通過量是供應側和需求側相互作用的結果，能夠準確反映當前航運發展的現實情況。選取具有一般性和代表性的實際國民生產總值(GDP，元)，其值以G表示，和三次產業實際產值X1，X2，X3(元)反映沿線經濟的發展狀況和沿河經濟帶產業結構，分析內河航運與沿河區域經濟之間的關聯性。船閘貨物通過量數據來源于蘇北運河內部統計數據，經濟數據來源于國家統計局網站以及各城市統計年鑒和江蘇省統計年鑒。

1.2 指標關聯性初步分析

指標關聯性大小可以從其數值走勢中發現，本文通過分析指標對數折線圖的發展趨勢，初步探尋指標間的關聯性。由于經濟數據大多是偏態分布，需要解決異方差問題，因此對實際GDP和三次產業產值取對數，分別表示為lnG、lnX1、lnX2和lnX3。如圖2所示，對數化消除數據波動之后，指標數據較為平穩，易于觀察指標數據發展趨勢。

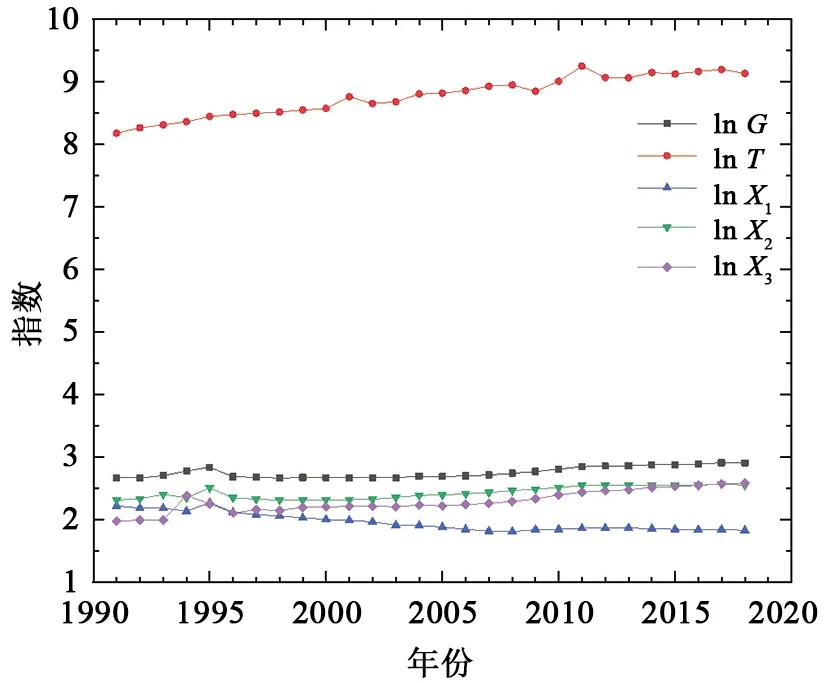
圖2 內河航運與區域經濟發展指標對數結果折線圖Fig.2 Log-linear graph of inland navigation and regional economic development

圖2顯示第一產業產值走勢在1995年小幅波動后，數值逐漸減少，而后緩慢趨于穩定，與內河航運貨運量走勢相反，表明兩者具有較弱的關聯性。第二、三產業產值以及實際地區生產總值總體平穩，走勢小幅緩慢向上，與內河航運貨運量走勢一致，可初步判定指標間具有較強的相關性。

1.3 灰色關聯度分析

限于時間跨度，本文采用基本方法灰色關聯度模型[14]。本文設計的灰色關聯分析的計算步驟如下：

(1)確定分析數列。本文將水運貨運量列為參考數列，G、X1、X2和X3為比較數列。設參考數列為X0=T(k)(k=1,2,…,n)，比較數列為Xi(i=1,2,3,4)。

(2)變量無量綱化。本文依據數據特性，選用均值化方法。

(3)X0(k)與Xi(k)的關聯系數計算公式見式(1)：

(1)

其中：ρ為分辨系數，取值區間為(0，1)，本研究取ρ=0.5；ξi(k)指變量i第k年的關聯度系數。

(4)灰色關聯度計算。求各個變量關聯系數平均值，關聯度ri計算見式(2)。

(2)

依照上述計算步驟，可計算得出蘇北運河歷年水運貨運量與沿河區域經濟和三種產業的灰色關聯度。第三產業產值與水運貨運量關聯度達到0.784，排名第一；隨后是第二產業產值與水運貨運量的關聯度達到了0.720，沿河區域實際GDP與水運貨運量關聯度為0.704；排最后的是第一產業產值與水運貨運量的關聯度，為0.552。結果說明內河航運與沿河區域經濟還有第二、三產業具有緊密的關聯性。內河航運與第一產業關聯性較低的原因在于，內河航運貨物運輸結構與產業結構發展水平相關，蘇北運河沿線產業結構為“三二一”形式，第一產業占比已低于15%。蘇北運河實際上承擔了沿河四個城市經濟發展的原材料運輸，這些原材料與第二、三產業發展息息相關，符合模型計算結果。

2 內河航運與區域經濟發展的協同性研究

2.1 平穩性檢驗

做時間序列分析前，需對指標數據進行平穩性檢驗。時間序列分析平穩性檢驗一般采用單位根檢驗，本文選用的準則為SIC(Schwarz information criterion)。時間序列檢驗類型選AIC(Akaike information criterion)、 SC(Schwarz criterion)、HQ(Hannan-Quinn criterion)下實際結果最小的情形，檢驗結果如表1、表2所示。

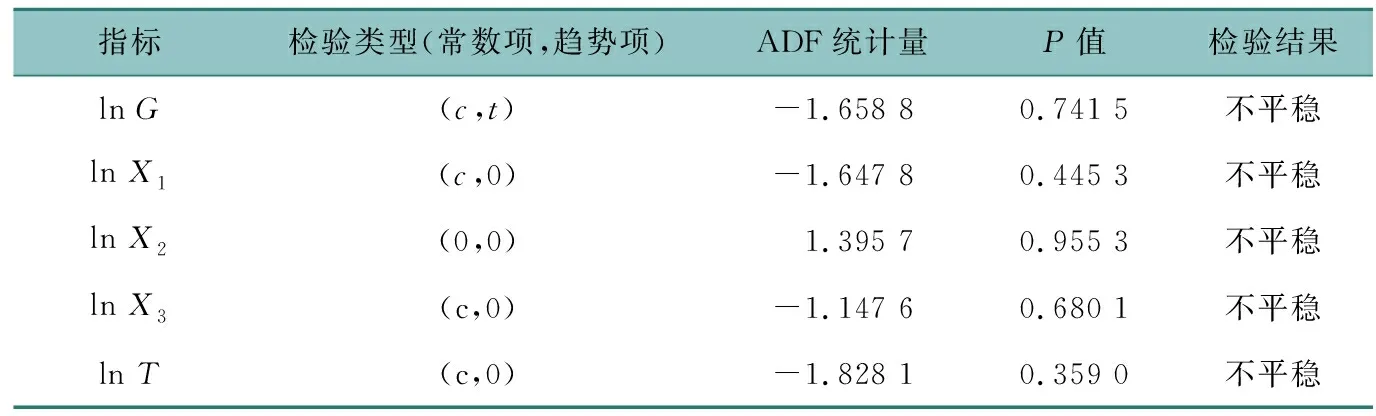
表1 原時間序列平穩性檢驗結果Table 1 Original results of stationarity test in time-series

表2 一階差分時間序列平穩性檢驗結果Table 2 Results of time-series stationarity test with first difference

表1結果顯示，原時間序列不平穩，取一階差分序列進行平穩性檢驗。在表2中，DlnG、DlnX1、DlnX2、DlnX3、DlnT分別為各指標的一階差分序列，檢驗結果表明在1%顯著性水平下，拒絕單位根假設，一階差分后的序列具有平穩性，即各指標時間序列均為一階單整，可以進行協整檢驗，指標一階差分結果如圖3所示。

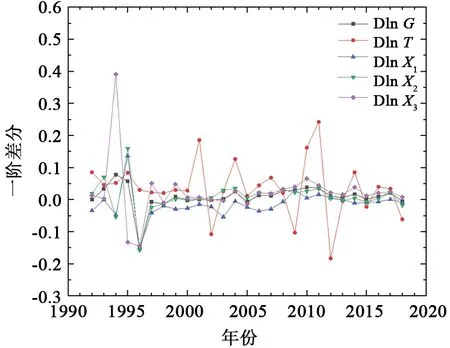
圖3 各指標一階差分序列圖Fig.3 First order difference sequence diagram of indices

2.2 最優滯后階數確定和Johansen協整檢驗

本文首先運用Eviews 10軟件，通過向量自回歸(vactor autoregression,VAR)模型估計[15]，將各準則下最小值最多的階數，判斷為最優滯后階數，同時保證VAR模型特征方程所有特征值倒數絕對值均小于1，使構建的VAR模型成立，確保最優滯后階數檢驗結果的有效性。然后進行Johansen協整檢驗，依次檢驗各經濟指標與水運貨運量的協整關系。曹永福[16]認為指標對數的差分可以定義為變化率，為探究內河航運與沿河區域經濟發展和產業結構的互動關系，在經濟發展方面，本文將分別研究lnT與lnG及DlnT與DlnG的協整關系；在產業結構方面，本文分別檢驗lnT與lnX1、lnX2和lnX3的協整關系。值得注意的是，前文的關聯度計算中，第三產業與貨運量關聯度最大，但此處結果顯示兩者未形成長期協整關系。灰色關聯度不能證明兩者間一定存在關系，僅表示兩者變化趨勢的相似度。現實原因可能在于我國各地區產業結構逐漸由“一二三”轉變為“三二一”，第三產業與貨運量持續增長的變化趨勢較第一、二產業更為相似，由此導致以量化發展趨勢相似性為目的灰色關聯度值最大。為節省篇幅，本文僅展示存在協整關系的最優滯后階數和Johansen協整檢驗結果，最優滯后階數結果如表3所示，協整關系檢驗結果如表4所示。

表3 最優滯后階數結果Table 3 Optimal lag order results

表4 協整關系檢驗結果Table 4 Co-integration test results

如表3所示，DlnT與DlnG之間的最優滯后階數為1階，lnT與lnX2間的最優滯后階數也為1階。

如表4所示，水運貨運量與沿河城市經濟存在協整關系，研究結果與王凱文等[6]一致。同時，沿河區域第二產業產值與水運貨運量存在協整關系。內河航運作為沿河區域經濟互動、要素分配的通道，加速了沿河區域投資、技術、自然資源和勞動力等的傳輸，發揮著內河航運作為中間產品型基礎產業對適配產業的輻射帶動功能；同時沿河區域經濟活躍，其發展需求讓適用于內河航運運輸方式的貨運種類和數量不斷增多，支撐著內河航運發展，逐步拓展成綜合運輸樞紐。

2.3 格蘭杰因果檢驗

為更準確描繪出內河航運與沿河區域經濟發展互動關系，定量研究指標間的影響作用方向，進行格蘭杰因果檢驗，檢驗結果如表5所示。

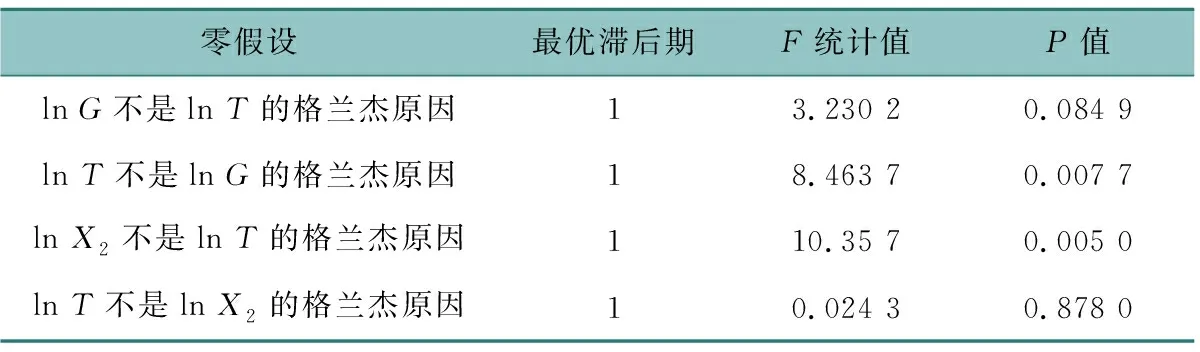
表5 格蘭杰因果關系檢驗結果Table 5 Granger causality test results

本文已確定最優滯后階數和已驗證指標間存在協整關系，很大可能上排除了“偽回歸”現象，此時格蘭杰因果檢驗有意義。水運運輸方式適用于長距離、大噸位的運輸，當水路運輸供給增加，對產業結構和經濟發展的影響存在差異。表5檢驗結果顯示，從統計學意義上來看，在1%顯著性水平上，第二產業支撐著內河航運發展，內河航運影響和推動著區域經濟發展；顯著性水平為10%時，沿河區域經濟也支撐著內河航運發展。沿河區域城市產業結構在逐步優化，第一產業比重逐年降低，第二、三產業占比逐漸增加。隨著經濟結構調整和專業分工的細化，企業對煤炭、原油等原材料的需求會增加，進而干散貨運輸、外貿運輸、大宗貨物運輸量的需求會大幅增加。根據蘇北航務管理處發布的歷年交通運輸服務報告可知，蘇北運河貨運種類主要為各種礦建材料與煤炭。2019年報告測算出蘇北運河所在流域地區社會經濟生產建設需求對煤炭需求約占年度運輸總量23.8%，對礦建需求約占年度運輸總量的83.2%。顯而易見，此兩類材料與社會經濟生產建設，尤其是第二產業發展密切相關，充分說明了沿河區域經濟和第二產業支撐著內河航運發展。計算結果符合實際現象，進一步證明內河航運與沿河區域經濟增長和第二產業發展的關聯性和相互影響、相互支撐和帶動的作用。

3 內河航運與沿河區域經濟發展的互動影響分析

3.1 VAR模型估計

前文確定了內河航運與沿河區域經濟增長、第二產業發展的相互影響關系。為進一步研究內河航運與區域經濟、第二產業的影響力度，本文對lnT與lnG、lnT與lnX2分別建立了VAR模型，運算結果如表6和表7所示。

表6 ln T與ln G模型參數估計結果Table 6 ln T and ln G model parameter estimation results

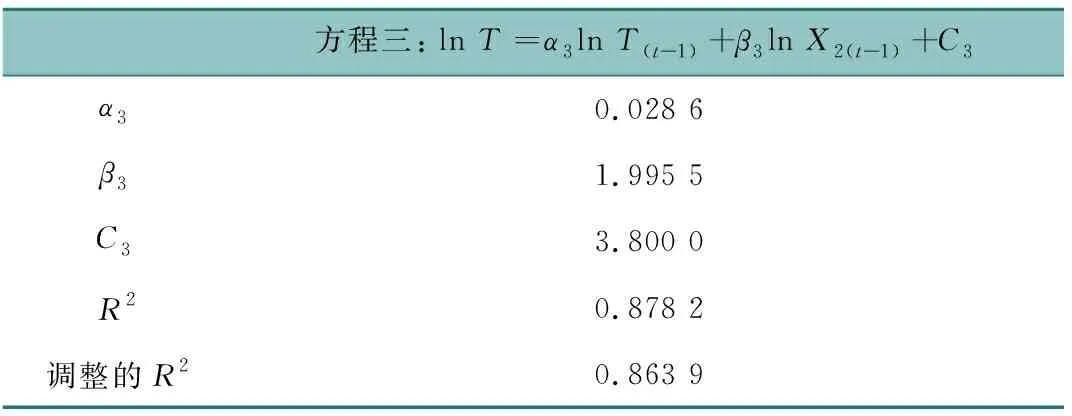
表7 ln T與ln X2模型參數估計結果Table 7 ln T and ln X2 model parameter estimation results

為了剔除自變量個數和樣本量對R2的影響，同時引入調整的R2。表6的估計結果中，方程一和方程二的相關系數R2和調整的R2均在0.8以上，擬合優度較好。方程中各回歸系數均為正值，說明內河航運與沿河區域經濟互為正向影響。方程一中，lnG(t-1)系數α1=0.834 0遠大于lnT(t-1)系數β1=0.041 6，表明上一年沿河區域經濟對內河航運的影響遠大于上一年內河航運發展情況對沿河區域經濟的影響。方程二中，lnT(t-1)系數β2=0.900 7遠大于lnG(t-1)系數α2=0.077 4，究其原因，當內河航運與沿河區域經濟均衡發展時，內河航運貨運量是通航能力的部分體現，若未對航道基礎建設投資改建，航道固有的物理通航能力限制著內河航運貨運量。

如表7所示，方程三的R2和調整的R2均在0.85以上，模型擬合優度較高，模型參數估計結果較可靠。lnX2(t-1)的系數β3=1.995 5較大且為正數，說明沿河區域第二產業上一年發展趨勢會明顯拉動內河航運發展。lnT(t-1)系數α3=0.028 6雖為正數，但相對前者系數而言數值很小，表明上一年的貨運量對內河航運發展有一定影響，但不顯著。通過方程二與方程三對比可知，第二產業發展情況對蘇北運河航運的支撐作用遠大于沿河區域經濟對蘇北運河航運的支撐作用。

3.2 脈沖響應分析

作者在估計VAR模型時，已通過單位圓檢驗方法，判定VAR模型穩定，如圖4所示。

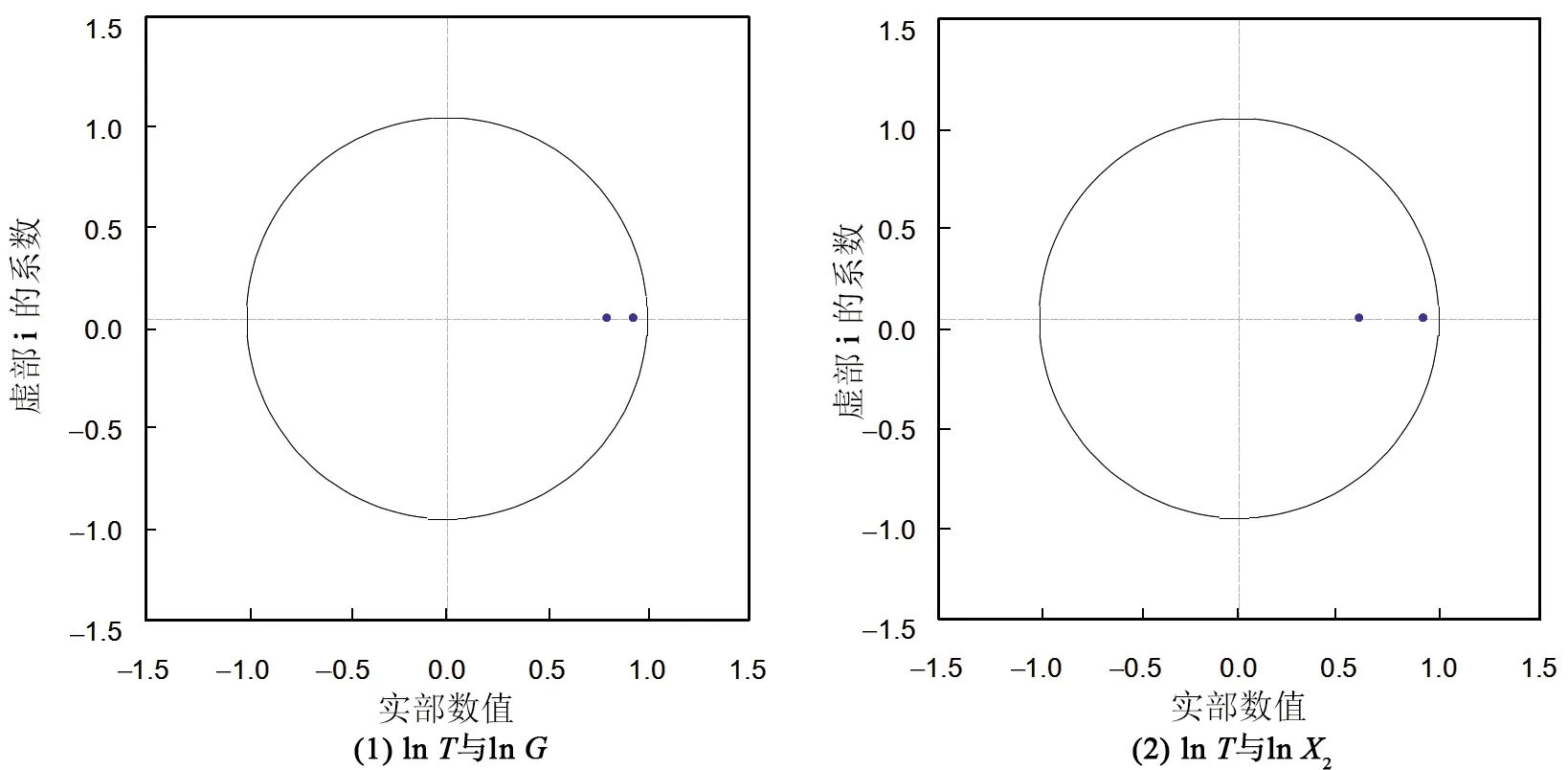
圖4 AR特征根倒數Fig.4 Reciprocal of AR eigenvalue

為進一步了解在標準差沖擊后對被解釋變量當前和未來的影響程度和方向，接著進行脈沖響應分析，并總結被解釋變量應對標準差沖擊的響應變化規律，脈沖響應圖如圖5所示。

圖5 脈沖響應圖Fig.5 Impulse response diagram

本文脈沖響應以一年為一期，如圖5(a)所示，沿河區域經濟對內河航運發展沖擊的響應，初期影響微弱，但從長期看，內河航運發展對區域經濟增長正效應逐漸增大并于第8期達到最大值，而后緩慢減小，并且這種正向帶動作用持續時間較長。如圖5(b)所示，呈現出沿河區域經濟發展對內河航運的正向拉動作用，拉動作用自第一期最大值逐期減小并趨于平穩，與方程二估計結果相似。如圖5(c)所示，第二產業發展對內河航運發展存在正向影響，圖中顯示沖擊作用在第二期和第三期時達到最大值0.026%，而后平穩下降，內河航運發展速度相對于第二產業發展速度是緩慢的。從三者沖擊響應程度來看，第二產業對內河航運發展的支柱作用更為顯著，大于沿河區域經濟對內河航運發展的支撐作用。此外，內河航運對沿河區域經濟的帶動作用雖一直存在，但影響程度相對經濟的支撐作用而言較小，分析結論同前文模型結果一致。京杭運河黃河以北段沿河區域經濟發展環境與蘇北運河相似，結合模型研究結果可知，若京杭運河黃河以北段復航，將集聚資金、人才、信息等資源，促使沿河區域產業，尤其是第二產業的集聚擴大，進而提升沿河區域活力，不斷增加商品交易和貿易發展的貨物運輸需求，推動復航航段航運功能進一步完善，實現內河航運帶動沿河區域經濟發展的良性循環模式。且京杭運河連接著黃河以南段大量經濟發達的東部沿海城市，能以低運輸成本實現資源優化配置，加速提升沿河區域經濟和產業發展活力。

4 某沿河產業園與京杭運河互動發展效果分析

本文選取徐州某新材料產業園作為分析對象，探尋內河航運與沿河區域經濟和產業的互動發展效果。該產業園位于船閘下游3 km，南靠京杭大運河，擁有兩大港口A和B，緊鄰物流園、徐州保稅物流中心，交通區位優勢顯著。

4.1 內河航運對沿河區域經濟和產業的貢獻分析

該產業園附近A港口2020年實現190.3萬噸的吞吐量，對營業收入的直接貢獻為2 419.86萬元，直接貢獻增加企業稅收120.85萬元，直接貢獻產生就業數119人，發放工資達445.89萬元。從港口吞吐量和營業收入間的相關性來看，該港口吞吐量和營業收入間的相關系數約達0.81，該項數據表明內河航運對城區經濟和產業的發展起到較為關鍵的推動作用，與上文研究結論相同。

4.2 沿河區域經濟和產業對內河航運的推動作用

以產業園附近A港口為例，從港口吞吐量和全區GDP關系來看，港口吞吐量和全區GDP的相關系數僅達0.194 6，這數據表明目前城區經濟的發展對內河航運發展的推動作用較不顯著，其仍有較大的提升空間，與上文研究結論一致。

5 結論

本文以蘇北運河沿河經濟帶主要城市宿遷、徐州、淮安和揚州為研究對象，通過灰色關聯度計算、協整檢驗、因果檢驗等方法初步探尋蘇北運河航運發展與沿河區域經濟發展趨勢的相互影響關系，并建立VAR模型定量描述蘇北運河航運發展與沿河區域經濟發展以及第二產業發展的關系，進而選取案例研究內河航運與沿河區域經濟和產業的互動效應，得出以下幾點結論：(1)沿河區域經濟和第二產業對蘇北運河航運發展的支撐作用持續存在，而蘇北運河航運也長期且正向帶動著沿河區域經濟的發展。(2)內河航運發展與沿河區域航運相關產業園區的發展密切相關，相互支撐和促進。(3)若京杭運河黃河以北段復航將對沿河區域經濟和產業發展發揮突出貢獻，加速資源優化配置，提升沿河區域經濟和產業發展活力。

針對現有內河航運缺點，結合研究結論，對京杭運河黃河以北段沿河區域規劃設計提出以下幾點建議：(1)優化沿河區域產業結構，有效支撐內河航運發展。第二產業仍是內河航運發展的重要支撐力量，應根據京杭運河黃河以北段沿河區域產業結構特色，推動第二產業集聚，以大項目推動大發展，強化第二產業對內河航運的支撐作用，推動實現京杭運河黃河以北段帶動沿河區域經濟發展的良性循環模式。(2)規劃沿河產業園集疏運體系，完善沿河區域綜合交通運輸體系。京杭運河黃河以北段航運受枯水期和豐水期影響較大，應盡可能規劃完善沿河產業園內部集疏運方式和周邊集疏運體系，實現公鐵水空四種運輸方式聯運，充分發揮內河航運優勢，提高物流運輸效率和降低物流運輸成本，帶動沿河區域發展。(3)運輸交接點拓展增值服務，推動沿河特色產業園區建設。鑒于內河航運與沿河產業園區的緊密聯系，建議在內河航運與公路、鐵路等各種運輸方式的交接點，根據客戶的需要拓展增值服務，輔助沿河區域構建特色產業園區，增強產業園區企業的市場競爭力。