例說幾道同構試題
蘇藝偉
(福建省龍海第一中學新校區 363100)
近年來,不少省市高考模擬試卷或者高考試題出現借助同構解決問題的試題.比如2020年全國Ⅰ卷理科第12題,2020年全國Ⅲ卷理科第11題,2020年山東高考理科第21題等.此類試題短小精悍,思維量大,綜合性強,含金量高,成為熱點.所謂同構,即將題目所給方程、不等式、代數式等變形成為具有相同結構的形式,然后抽象出一個函數,借助該函數的單調性解決問題.其關鍵在于觀察式子的結構特征,進行恰當轉化,從而發現式子結構中隱含的共性,內在聯系.
例1(2021年福建高三四月診斷性練習)已知實數a,b滿足a=e5-a,2+lnb=e3-lnb,則ab=____.
分析本題以方程為載體考查指數式、對數式的運算,以及能否借助同構的思想解決問題.試題體現高考評價體系提出的綜合性和創新性要求,突出對數學運算素養、邏輯推理素養的考查.
解析由2+lnb=e3-lnb,得2+lnb=e5-(2+lnb).
由于a-e5-a=0,2+lnb-e5-(2+lnb)=0,
故令f(t)=t-e5-t,則f(a)=f(2+lnb).
又f′(t)=1+e5-t>0,
所以f(t)在R上單調遞增.
故a=2+lnb.
則ab=(2+lnb)b=e3-lnbb=e3-lnbelnb=e3.
評注解題的關鍵在于得到兩個形式一樣的方程,第一個是a-e5-a=0,第二個是2+lnb-e5-(2+lnb)=0,從而聯想到構造函數f(t)=t-e5-t,結合單調性求解.
變式1 已知實數α,β滿足αeα=e3,β(lnβ-1)=e4,則αβ=____.

由αeα=e3,得eαlneα=e3.



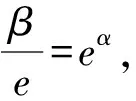
則αβ=α·e·eα=αeα·e=e4.
變式2已知實數a,b滿足a=e7-a,3+lnb=e4-lnb,求ab=____.
解析由3+lnb=e4-lnb,得3+lnb=e7-(3+lnb).
令f(x)=x-e7-x,
由f′(x)>0得f(x)在R上單調遞增.
又f(0)<0,f(6)>0,所以f(x)只有一個零點.
由f(a)=f(3+lnb),得a=3+lnb.
所以b=ea-3.
故ab=e7-aea-3=e4.

解析由已知可得aex+lna-ln(x+2)-2>0,
elna+x+lna>ln(x+2)+2.
即elna+x+x+lna>ln(x+2)+x+2.
故elna+x+x+lna>eln(x+2)+ln(x+2).
構造函數g(t)=et+t,則
g(x+lna)>g[ln(x+2)].
又g(t)在R上單調遞增,
所以x+lna>ln(x+2).
即lna>ln(x+2)-x.
令h(x)=ln(x+2)-x,易求得h(x)的最大值為h(-1)=1,所以lna>1,即a>e.
評注將題目所給不等式變形成為elna+x+x+lna>eln(x+2)+ln(x+2),進而構造出函數g(t)=et+t,借助單調性求解.
例3(東北師范大學附屬中學2020屆高三模擬考試)已知實數x,y滿足ln(4x+3y-6)-ex+y-2≥3x+2y-6,求x+y的值.
解析設m=4x+3y-6,n=x+y-2,
則m-n=3x+2y-4.
故lnm-en>m-n-2.
即lnm-m+lnen-en≥-2.

則f(t)在(0,1)單調遞增,在(1,+∞)單調遞減,所以f(t)max=f(1)=-1.
故f(t)≤-1.
所以f(m)≤-1,f(en)≤-1.
則f(m)+f(en)≤-2.
又f(m)+f(en)≥-2,故只能是
f(m)+f(en)=-2,
此時f(m)=-1,f(en)=-1.
則m=1,en=1,n=0.
則4x+3y-6=1,x+y-2=0.
解得x=1,y=1.所以x+y=2.
評注將題目所給不等式變形成lnm-m+lnen-en≥-2,進而構造出函數f(t)=lnt-t,借助單調性求解.
例4(武漢市2019屆高三模擬考試)已知函數f(x)=ex-aln[a(x-1)]+a,a>1.關于x的不等式f(x)>0恒成立,則實數a的取值范圍是____.

ex-lna+(x-lna)>ln(x-1)+eln(x-1).
令f(t)=et+t,則f(t)在R單調遞增.
由f(x-lna)>f[ln(x-1)],得
x-lna>ln(x-1).
故x-ln(x-1)>lna.
記g(x)=x-ln(x-1),x>1,
故g(x)在(1,2)單調遞減,在(2,+∞)單調遞增,所以g(x)min=g(2)=2.
故lna<2,解得0 評注將題目所給不等式變形成ex-lna+(x-lna)>ln(x-1)+eln(x-1),進而構造出函數f(t)=et+t,借助單調性求解. A.sinx1 C.sinx1+cosx1>sinx2+cosx2 D.sinx1+sinx2>cosx1+cosx2 解析由已知,有 則sinx1=sin(x1+x2),所以A錯誤. 則sinx1+cosx1 同理sinx2>cosx1. 所以sinx1+sinx2>cosx1+cosx2. 綜上,故選D. 例6(2017清華自招試題)已知實數a,b滿足a2+a=3b2+2b(a>0,b>0),則( ). A.a>bB.a 解析由a2+a=3b2+2b,得a2+a<4b2+2b. 令f(x)=x2+x,x>0,易知f(x)在(0,+∞)上單調遞增.又f(a) 同理,由a2+a=3b2+2b,得a2+a>b2+b. 令f(x)=x2+x,x>0,易知f(x)在(0,+∞)上單調遞增.又f(a)>f(b),所以a>b. 評注將題目所給式子變形成a2+a<4b2+2b或者a2+a>b2+b,進而構造出函數f(x)=x2+x,x>0,借助單調性求解. 通過上述例題不難發現,利用同構思想解決問題,求解的關鍵在于將不等式或者方程進行不斷變形和轉化,直到不等式或者方程兩邊出現相同的結構式子,最后構造函數,利用函數的單調性解決問題.在實際解題中必須認真觀察式子的結構特征,善于聯想和轉化,充分挖掘題目結構式隱含的共性特征.