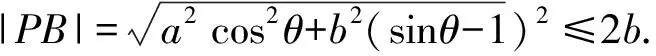淺談構造法解圓錐曲線中離心率范圍問題
沈 濤
(陜西省寶雞市石油中學 721015)
一般來說,求解范圍問題多構造不等式求解或者構造函數求值域、離心率的范圍問題,還要結合相應的圓錐曲線的定義和性質,構造基本量a,b,c的不等式湊出離心率從而求解,或者構造離心率e關于某個變量的函數求值域,近年來,離心率范圍問題主要有以下幾種類型.
1 構造一元二次方程,利用韋達定理
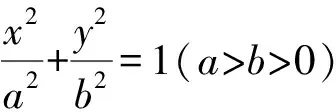

轉化為方程即(k-1)[b2k2+(b2-a2)k+b2]=0有三個不相等的正實根.
解得3b2 利用題意結合圖形(如點在曲線內等)列出所討論的基本量(a,b,c)適合的不等式(組),通過解不等式組得出離心率的變化范圍. 分析由題意設B(x0,y0)(-a 本題是最常見的求離心率范圍的問題,其方法就是根據已知條件,直接列出關于a,b,c間的不等量關系,然后利用a,b,c間的平方關系化為關于a,c的齊次不等式,除以a2即為關于離心率e的一元二次不等式. 把所討論的離心率作為一個函數的自變量來表示這個函數,通過討論函數的值域來求離心率的變化范圍. 分析由橢圓的定義及對稱性求得|AF|+|BF|=2a. 在Rt△ABF中利用直角三角形的性質求得 |AF|=2csinα,|BF|=2ccosα. 所以2csinα+2ccosα=2a. 分析由已知a2=m2+4,b2=3, 則c2=a2-b2=m2+4-3=m2+1. 分析設|PF1|=m,|PF2|=n,根據余弦定理得出mn,則m+n=2a. 由余弦定理,得 所以a2cos2θ+b2(sinθ-1)2≤4b2. 在求解圓錐曲線離心率取值范圍時,一定要認真分析題設條件,合理構造a,b,c的不等關系或e關于某個變量的函數,把握好圓錐曲線的相關性質,靈活運用構造法,從而達到快速解題的目的.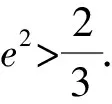

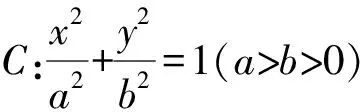
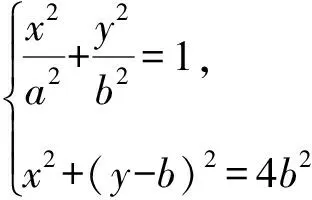

2 結合圓錐曲線定義及焦半徑性質
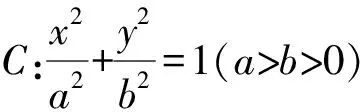
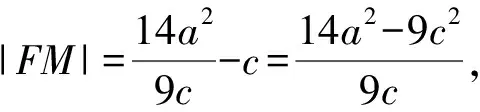

3 構造不等式(組)求解
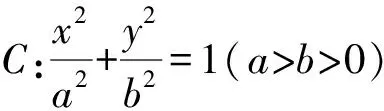


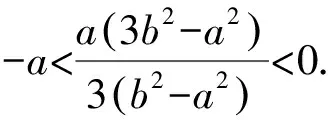
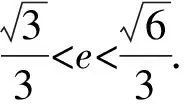
4 構造函數求值域求解
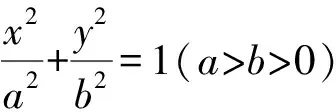
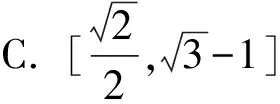

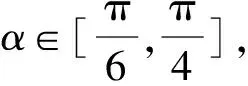



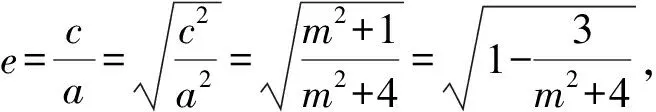
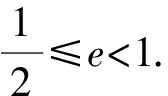
5 利用余弦定理構造均值不等式


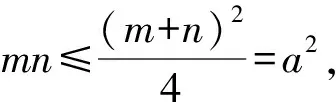
6 利用三角函數的有界性構造不等式