利用導數多視角研究一道壓軸題
李昌成
(新疆烏魯木齊市第八中學 830002)
1 試題呈現
題目已知曲線f(x)=lnx+2x與曲線g(x)=a(x2+x)有且只有兩個公共點,則實數a的取值范圍為( ).
A.(-∞,0) B.(0,1] C.(0,+∞) D.(0,1)
2總體分析
此題是2022年一輪復習測試卷中的選擇題的壓軸題,通過仔細分析,筆者發現有幾種不同的方法來解決此題:可以轉化為函數零點問題來解決;可以聯立方程組,轉化為有兩個實數根,再運用合適的方法化歸與轉化來解決;基于兩個函數有公共點,利用隔離直線,借助于凸凹翻轉和數形結合來解決;也可以聯立后,部分變形,化曲為直,借助臨界的切線作為工具來解決.以下具體來探討和展示求解過程,并進行類題的歸納和整合.
3 試題解答
視角1 利用函數零點求解.
解法1記h(x)=a(x2+x)-(lnx+2x),則問題轉化為h(x)=0有兩個零點.
求導,得
因為x>0,當a≤0時,h′(x)<0.
所以函數h(x)=a(x2+x)-(lnx+2x)單調遞減,至多只有一個零點,不滿足題意.


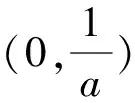


評注此處直接轉化為函數零點問題求解,此時需要對字母參數的正負進行討論,再結合導數的正負得出原函數的增減,求出相應的最值,最后得出不等式求出結果,基本上就是一道解答題的運算量,作為選擇題,有些得不償失.
視角2 分離變量作答.
解法2 根據題意可知函數f(x)的定義域為(0,+∞),兩曲線y=f(x)與y=g(x)有且僅有兩個公共點,則方程lnx+2x=a(x2+x)有兩個實數解.
由x>0可知x2+x>0.
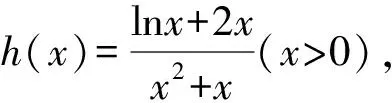
問題轉化為直線y=a與函數y=h(x)的圖象有兩個不同的交點.
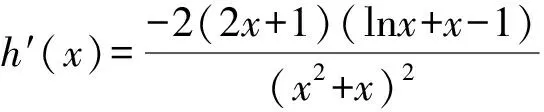
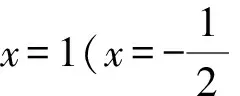
由h′(x)>0,得0 由h′(x)<0,得x>1. 所以y=h(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減. 所以h(x)≤h(1)=1. 又x→0+時,h(x)→-∞; x→+∞時,h(x)→0且h(x)>0. 若使直線y=a與y=h(x)有兩個交點,則需要0 評注此解法利用函數圖象的交點與方程根的聯系進行轉化,建立等式關系,接著進行變量分離,轉化為直線y=a與函數y=h(x)的圖象有兩個不同的交點,通過對y=h(x)求導,用導數判斷出單調性,作出函數的準確圖象,然后上下移動參數的值,看直線與函數交點個數即可. 視角3 利用兩曲線相切的臨界值求解. 解法3 由已知條件易知f(x)=lnx+2x為上凸函數,欲使曲線f(x)與g(x)有兩個公共點,則必有a>0. 所以g(x)=a(x2+x)為開口向上的二次函數,且為下凸函數. 不妨設兩函數切于點P(x0,y0),分別求導,得 ① ② 代入①整理,得 所以lnx0+x0=1.解得x0=1.所以a=1. 所以0 評注解決兩曲線的交點問題,可以采用數形結合思想,根據函數的圖象或者趨勢圖象,找出符合題意的條件即可.因此,用導數的幾何意義找出臨界的公切線,同時確定a的臨界值,再結合圖象得出參數的取值范圍,這種方法用來解決導數壓軸小題還是行之有效的. 視角4 利用化曲為直思想求解. 解法4由解法2,兩曲線f(x)與g(x)有且僅有兩個公共點,則方程lnx+2x=a(x2+x)有兩個實數解,且x>0. 所以lnx+2x=ax(x+1). 所以切線方程為 而直線y=a(x+1)-2恒過點(-1,-2), 化簡,整理得 -(2x0+1)(x0-1)=(2x0+1)lnx0. 又x0>0,所以lnx0=-x0+1. 所以0 視角5去偽存真排除干擾. 解法5 令h(x)=lnx+2x-a(x2+x),則h(x)有兩個零點. 當a=1時,h(x)=lnx+x-x2, 令h′(x)>0,得0 令h′(x)<0,得x>1. 則h(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減. 所以h(x)max=h(1)=0,只有一個零點,與已知矛盾,故a≠1,排除B,D. 當a=-1時,h(x)=lnx+3x+x2, 所以h(x)在(0,+∞)上單調遞增,從而h(x)>h(0)=0,無零點,與已知條件矛盾,故a≠-1,排除C,故選A. 近幾年,兩函數圖象交點問題、函數的零點問題在選擇題、填空題以及解答題中都出現過,該問題主要考查函數與方程的關系,要求學生能夠用分類討論、數形結合、轉化與化歸的思想來解決問題.對于復雜的非初等函數,利用導數的幾何意義及導數來判斷函數的單調性等來處理,問題就不難解決了.因此,學好導數對我們更好地理解函數有積極作用. 當然,解題中的不同思想和策略需要學生逐漸領悟,高考復習的終極目標是讓學生學會獨立解題.因此,對于經典試題,教師要引導學生從不同的角度進行思考,尋求多種解法.培養學生的發散思維,培養學生良好的思維品質,發展創造性思維.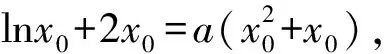
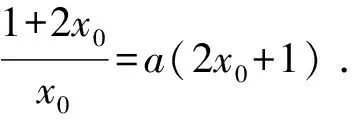
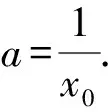


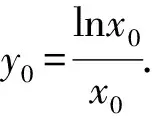
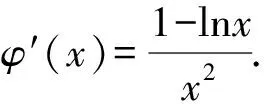
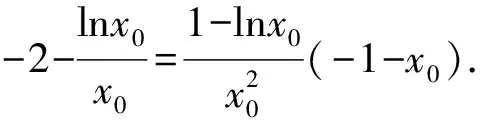
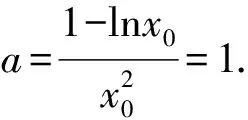

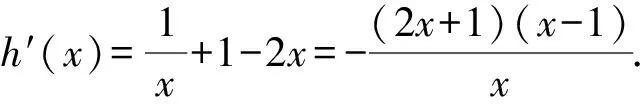
4 解后反思

