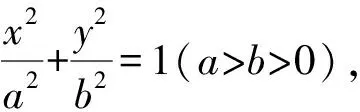2020年全國高考Ⅰ卷理科數學第20題的解法與變式拓展
李文東
(廣東省中山市中山紀念中學 528454)
2020年全國Ⅰ卷理科數學第20題以直線和橢圓為背景,考查圓錐曲線的基本知識和直線過定點問題,考查轉化與化歸思想、推理論證能力、運算求解能力,體現了數學運算、數據推理等核心素養,是一道難得的好題,值得我們細細研究,下面我們給出本題的幾種典型的解法,并從不同角度給出了一些拓展.
1 題目呈現
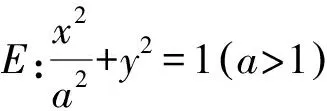
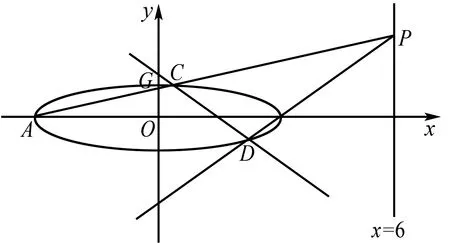
圖1
(1)求E的方程;
(2)證明:直線CD過定點.
2 題目解析
2.1 第(1)問解析
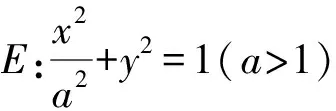
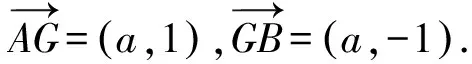
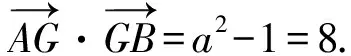
所以a2=9.
2.2 第(2)問解析
證法1 設P(6,y0),則直線AP的方程為
聯立直線AP的方程與橢圓方程得
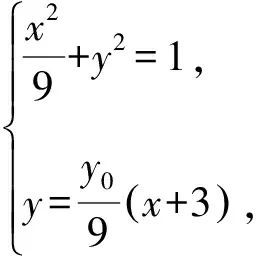
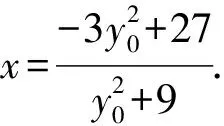
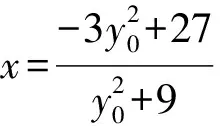
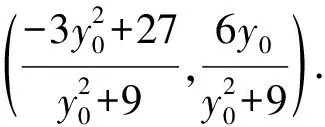

所以直線CD的方程為
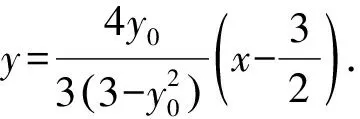

評注用點P(6,y0)的坐標表示C,D的坐標,進而求出直線CD的方程,此解法的優點是思路自然,但缺點也很明顯,就是運算量較大.
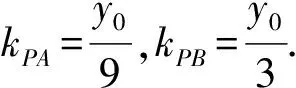
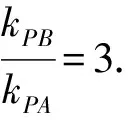
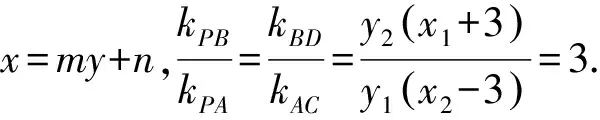

(m2+9)y2+2mny+n2-9=0.
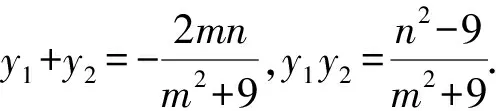
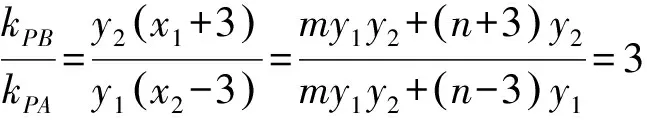
策略1合理運用韋達定理.
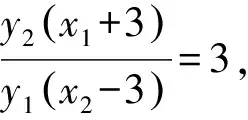
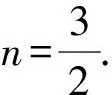

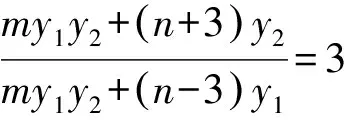
策略2恰當消元,減少變量個數.
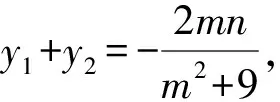
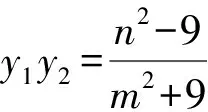
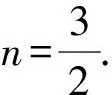
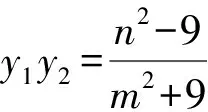
策略3合理利用曲線方程簡化運算.
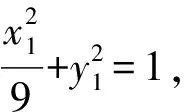
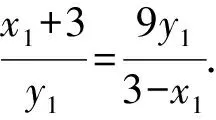
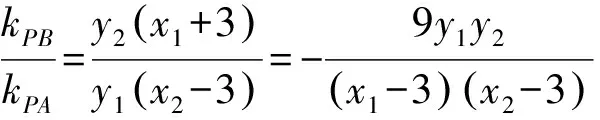
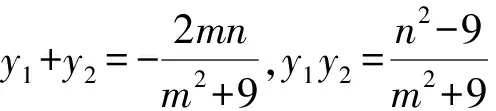
代入,得
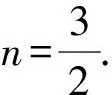

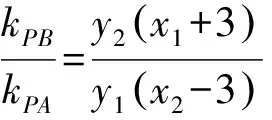

在此變換下直線x=6變為x′=2,點A,B變為A′(-1,0),B′(1,0).
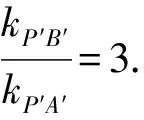

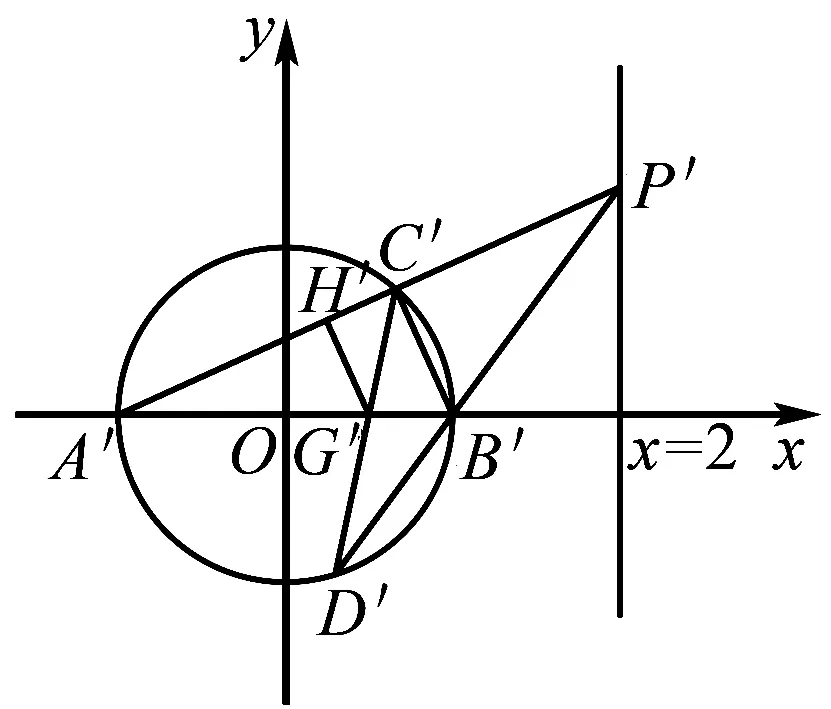
圖2
則tan∠P′B′x=tan∠A′B′D′=tan∠A′C′D′=3tan∠C′A′B′.
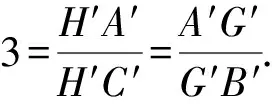
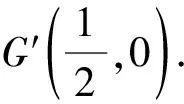
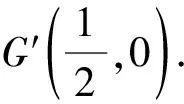
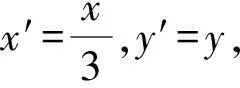
評注通過仿射變換化橢圓為圓來處理,然后利用圓的幾何性質順利解決問題,想法很巧妙,計算量很小,值得我們學習.除了以上幾種解法外,本題還可以利用曲線系的方法求解,限于中學教學實際,這里我們就不細說.
3 問題拓展
從橢圓和直線的角度來看,本題可以拓展如下:
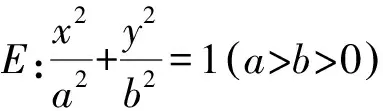
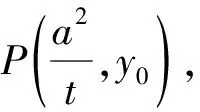
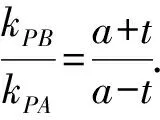

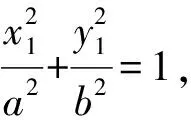

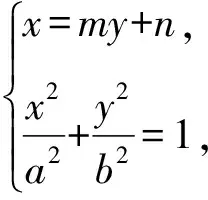
(a2+m2b2)y2+2mnb2y+(n2-a2)b2=0.
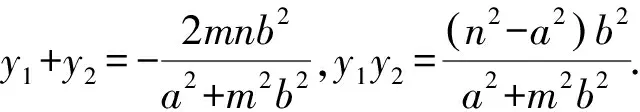
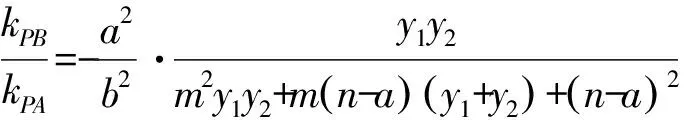
于是n=t,直線CD過定點(t,0).
如圖3,用幾何畫板演示其結果是正確的,其本質是圓錐曲線中的極點和極線問題,但是用初等數學證明很困難.在雙曲線和拋物線中也有類似的結論,這里不再贅述.
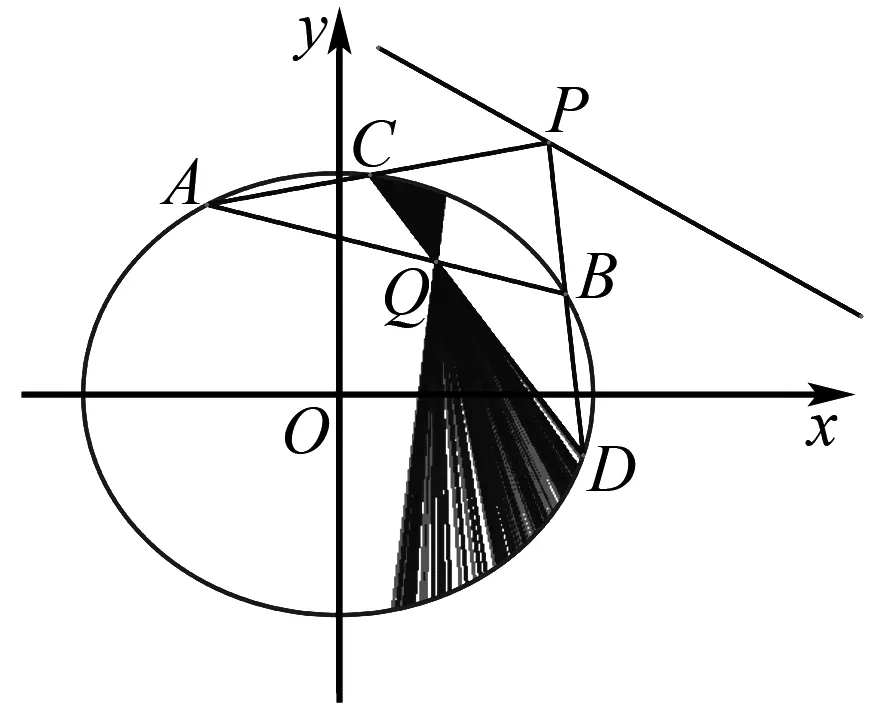
圖3
從斜率的角度考慮,本題也可以拓展如下:
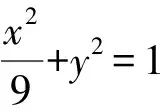
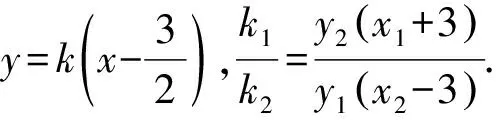
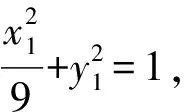
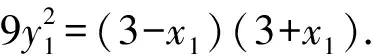
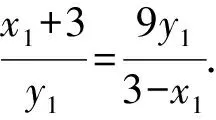

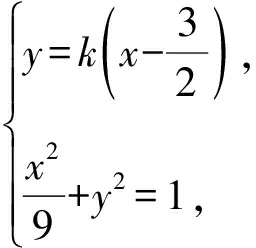
(36k2+4)x2-108k2x+81k2-36=0.
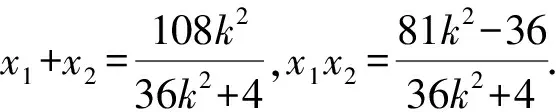
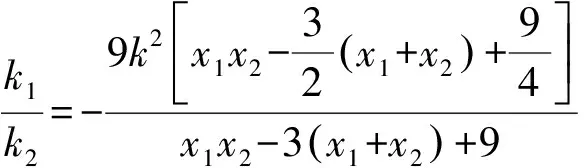
=3.
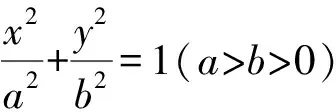
從逆命題的角度,我們可以得到如下問題:
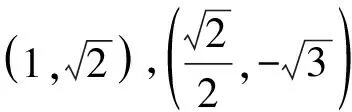
(1)求橢圓C的方程;
(2)過點M(0,1)的直線l與橢圓C交于不同兩點P,Q(異于頂點),記橢圓與y軸的兩個交點分別為A1,A2,若直線A1P與A2Q交于點S,證明:點S恒在直線y=4上.
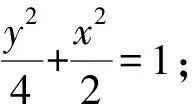
(2)由題意可設直線l的方程為y=kx+1,P(x1,y1),Q(x2,y2).
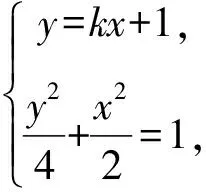

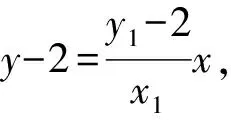
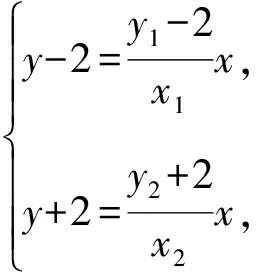
結合目標,消去x,得
(y2+2)x1(y-2)=(y1-2)x2(y+2).
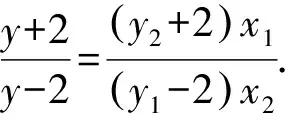
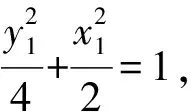
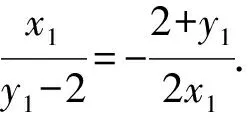

將韋達定理代入,得
從而y=4,即點S恒在直線y=4上.