近年來高考數學試題中概率與統計試題探析
黃鐘慧 廖小蓮
(湖南人文科技學院數學與金融學院 417000)
在概率與統計客觀題和主觀題的解題中,我們通常要弄清楚所給題目所涉及到的概率類型是否與抽樣方法、互斥事件、獨立事件、古典概型、幾何概型等有關,針對不同的類型問題都有不同的解決方法,從而使未知變已知,來提高學生的解題效率.這些文獻主要探討利用概率的加法公式和概率的乘法公式求獨立事件的概率、利用古典概型和幾何概型的公式求古典概型和幾何概型的概率、利用表格數據求解平均值和方差并利用題干做出科學決策、利用計算分布列和數學期望作出科學決策、利用計算數據求出K2與臨界值表作對比并作出科學決策.通過閱讀文獻,我發現離散型隨機變量的分布列及其期望是近幾年高考題目中概率與統計問題的熱點,這類問題主要考查學生理解題目的能力與思考問題能力,本文也有所體現.在高考題中的概率與統計的選擇題中,通常考查的題型有:抽樣方法、互斥事件、獨立事件、古典概型、幾何概型;在解答題中,通常考查的題型有:樣本估計總體、獨立性檢驗、回歸方程、離散型隨機變量的分布列及其期望值.
1 互斥事件與獨立事件的概率題型分析
一般地,事件A(或B)的發生不會影響事件B(或A)發生的概率,此時事件A和事件B稱作相互獨立事件,在一次隨機試驗中,事件A和事件B不能同時發生,則這兩個不能同時發生的事件叫做互斥事件.
例1(2021年全國Ⅰ卷理科第8題)有6個相同的球,分別標有數字1,2,3,4,5,6,從中有放回的隨機取兩次,每次取1個球,甲表示事件“第一次取出的球的數字是1”,乙表示事件“第二次取出的球的數字是2”,丙表示事件“兩次取出的球的數字之和是8”,丁表示事件“兩次取出的球的數字之和是7”,則( ).
A.甲與丙相互獨立 B.甲與丁相互獨立
C.乙與丙相互獨立 D.丙與丁相互獨立
分析我們可以先寫出兩點數之和為8的基本事件,再寫出兩點數之和為7的基本事件.再根據獨立事件的概率公式求解.
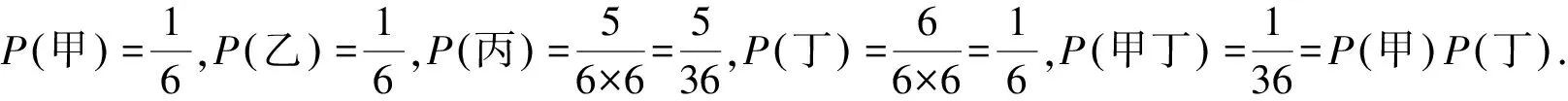
小結本題考查事件獨立性的概念,易錯點在于考生獨立性事件概念理解不夠透徹,容易混淆獨立性概念與條件概率.
2 幾何概型與古典概型的概率題型分析
幾何概型的特點:(1)無限性,試驗中所有可能出現的結果(基本事件)有無限多個;(2)等可能性,每個基本事件出現的可能性相等.具有以下兩個特點的概率模型稱為古典概型.古典概型的特點:(1)有限性——試驗中所有可能出現的基本事件只有有限個;(2)等可能性——每個基本事件的出現可能性相等.



小結本題考查長度幾何概型的概率計算,可計算出基本事件與所要求事件所包含的長度、區域、面積、體積等,最后運用幾何概型的計算公式計算即可得出答案.
例3(2020年江蘇卷理科第4題)將一顆質地均勻的正方體骰子先后拋擲2次,觀察向上的點數,則點數和為5的概率是____.
分析可以先寫出骰子先后拋擲2次點數之和所有的基本事件,再寫出點數之和為5的基本事件,最后利用古典概率的公式進行計算.
解析設事件A為將一顆質地均勻的正方體骰子先后拋擲2次,骰子向上的點數之和為5.
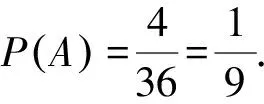
小結本題考查古典概型的概率計算,可列舉出所有的基本事件,再從中數出滿足條件的基本事件的個數,最后利用古典概型的計算公式計算即可得出答案.
3 離散型隨機變量的分布列與數學期望的概率題型分析
離散型隨機變量及其分布列可以一一列舉出隨機變量及其發生的概率,進而得到概率分布列,有利于分析數據;相互獨立事件概率乘法公式可以反映獨立事件發生的概率;期望綜合了隨機變量的取值和取值范圍的概率,反映隨機變量的平均水平.
例4(2021年全國Ⅰ卷理科第18題)某學校組織“一帶一路”知識競賽,有A,B兩類問題,每位參加比賽的同學先在兩類問題中選擇一類并從中隨機抽取一個問題回答,若回答錯誤則該同學比賽結束;若回答正確則從另一類問題中再隨機抽取一個問題回答,無論回答正確與否,該同學比賽結束.A類問題中的每個問題回答正確得20分,否則得0分;B類問題中的每個問題回答正確得80分,否則得0分.己知小明能正確回答A類問題的概率為0.8,能正確回答B類問題的概率為0.6,且能正確回答問題的概率與回答次序無關.
(1)若小明先回答A類問題,記X為小明的累計得分,求X的分布列;
(2)為使累計得分的期望最大,小明應選擇先回答哪類問題?并說明理由.
分析(1)通過理解隨機變量的分布列的定義和計算方法可以求出X的分布列;
(2)利用期望公式,分別求出回答A,B類問題的數學期望,根據比較,作出決策.
解析(1)由題意得,A類問題中的每個問題回答正確得20分,否則得0分,那么X的所有可能取值為0,20,100.即
所以X的分布列為:

表1
(2)當小明先選擇回答A類問題,由題意,得
E(X)=0×0.2+20×0.32+100×0.48=54.4.
當小明先選擇回答B類問題,記Y為小明的總共得到的分數,則Y的所有可能取值為0,80,100.
P(Y=0)=1-0.6=0.4,
P(Y=80)=0.6×(1-0.8)=0.12,
P(Y=100)=0.8×0.6=0.48,
所以Y的分布列為:

表2
E(Y)=0×0.4+80×0.12+100×0.48=57.6.
因為57.6>54.4,所以E(X) 小結這道題考查分布列、期望并通過期望作出科學決策.針對求每一個隨機變量的概率從而得到分布列;針對求離散型隨機變量的數學期望的問題時,我們可以把分布列表格的數字,每一列相乘后相加即可求出數學期望. 概率與統計問題是高考數學中的重要考查內容之一,我們需要牢牢掌握概率與統計方面相關的知識點.在解決概率統計問題時,我們首先要考慮這道題的類型,針對不同的類型有不同的解決方法.例如,在針對互斥事件、獨立事件的概率問題時,我們可以利用概率的加法和乘法公式解決這類問題.在針對離散型隨機變量的分布列及其期望的問題時,我們可以先理解X的含義,寫出X可能取得的所有值;其次求X取每個值的概率;再寫出X的分布列;最后根據分布列按照公式計算期望等.

