一種帶有觀測器的飛行器性能預設控制方法*
張 遠 黃萬偉 田 燦
1. 北京航天自動控制研究所,北京 100854 2. 宇航智能控制技術國家級重點實驗室,北京 100854
0 引言
高超聲速飛行器(Hypersonic Flight Vehicle, HFV)指的是一類飛行馬赫數大于5的飛行器,其航程遠、速度快,可實現低成本天地往返,具有廣闊的軍用和民用前景[1]。由于系統表現為強非線性、快時變性的動力學特性,同時氣動參數、機體參數存在大范圍攝動,對姿態控制提出了更高的要求和挑戰,成為近年來控制領域研究的重點之一。
近年來,學者們開展了諸多HFV控制系統的設計與研究,形成了一系列典型的控制方案架構。其中,反步法簡化了針對高階非線性系統直接設計控制器的難度,成為研究重點之一,其核心思想是將高階非線性系統控制問題分解為多個不超過系統階次的子系統,遞歸設計Lyapunov保證子系統逐步穩定,最后獲得整個系統的Lyapunov穩定,實現指令的跟蹤控制。文獻[2]通過設計一種滑模微分器估計虛擬指令的微分信號,緩解“計算膨脹”情況,同時研究了攻角非對稱時變約束控制;文獻[3]進一步關注工程中的航跡傾角難測量的應用難點,用高度和速度測量值以及高階微分器設計了航跡傾角在線估計方法,基于反步法設計航跡傾角子系統控制器,同時引入輔助系統降低執行機構飽合帶來的負面影響;文獻[4]則提出基于高階跟蹤微分器的減步控制方案,利用其對給定信號任意階導數精確估計的能力,減少設計步驟,再結合擴張狀態觀測器(ESO, Extended State Observer)獲得綜合擾動值,用于補償控制;文獻[5]針對HFV的縱向模型,將其分為速度和高度子系統,且把虛擬控制律設計中需要的導數作為不確定的一部分,設計自適應律應對含有未知上界的不確定性,避免了指令求導,實現速度和高度的精確跟蹤。
然而,上述的控制方案可以保證系統以指數形式收斂,沒有考慮控制系統的暫態性能和穩態性能(如超調、收斂時間、問題誤差),如果可根據預先設計的約束條件使得系統收斂時間可調、穩態精度可控,則具有較強的工程意義。因而,近年來能夠滿足這一需求的性能預設控制(PPC, Prescribed Performance Control)得到了學者們的廣泛關注[6-9]。文獻[6]針對彈性HFV的高度和速度通道設計指數型性能預設函數;文獻[7]研究了一種適應誤差初值未知的性能預設控制方法,利用神經網絡反演控制和最小參數方法,針對縱向模型子系統設計性能預設控制器;文獻[8]分別針對速度子系統和高度系統設計PI和反步法性能預設控制器,用單隱層神經網絡逼近系統不確定性;文獻[9]則在對存在執行故障的建模基礎上,設計基于有限時間衰減的預設性能函數,采用反步法設計有限時間性能預設控制器。
基于上述文獻的啟發,本文旨在針對HFV的縱向姿態通道,設計一種時間可設定的性能預設控制方案,并通過數值仿真校驗了該方案在存在復合時變干擾情況下的控制性能,主要貢獻如下:
1)提出一種時間可設定新型預設性能函數,在此基礎上設計基于反步法的性能預設控制律,能夠保證在設定時間內保證跟蹤誤差收斂至設定約束域,且收斂速度可根據需求靈活調節;
2)設計有限時間收斂擴張狀態觀測器,相對于傳統擴張狀態觀測器,可保證其更快的收斂速度,保證系統的控制精度;
3)因反步法需要指令微分項存在的“計算膨脹”情況,引入一種改進的跟蹤微分器緩解該問題。
1 問題描述
1.1 模型說明
考慮工作在水平無側滑狀態時的HFV,側滑角β和傾側角μ都為0,縱向和橫側向可相互解耦,則HFV模型可簡化為式(1)所示[10]。
(1)
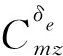
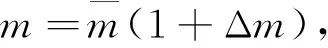

(2)
其中,Δα和ΔQ表示包含參數攝動和外界時變干擾的集總擾動。將式(2)寫成形如式(3):
(3)
1.2 控制目標
由1.1節中的帶有集總擾動的模型可知,HFV在飛行過程中經歷大包線飛行,其飛行環境及機體參數都將出現大范圍攝動,對于控制性能提出較大的挑戰。因此,若存在持續性擾動,則無法保證暫態控制精度,穩態精度也無法持續滿足。若以攻角為例,將其跟蹤誤差進行暫態性能和穩態性能兩方面的精確約束,則可達到時變擾動下的高精度控制需求。可定義攻角的跟蹤誤差預設性能條件如下:
-δαLρfα(t)
(4)
其中,ρfα(t)為攻角跟蹤誤差的性能預設函數,其約束了期望的暫態性能(如收斂速度、最大超調)和穩態性能(如跟蹤穩態誤差)。δαU和δαL分別為設定的誤差上、下界,滿足δαU,δαL∈(0,1]。
本文的主要控制目標為:1)系統輸出攻角α能夠精確跟蹤給定的時變攻角指令αc;2)在存在時變集總干擾的情況下,暫態響應滿足設計需求,穩態誤差在預先設定的范圍之內。
2 新型性能預設反步控制器
本節針對縱向姿態系統設計新型性能預設控制器,主要由4部分構成:1)針對攻角子系統和角速度子系統引入性能預設函數,并對受約束的跟蹤誤差進行無約束轉換;2)利用反步法進行姿態系統控制器設計;3)針對反步控制律中用到的指令微分項,引入跟蹤微分器;4)針對集總擾動,設計有限時間擴張狀態觀測器,獲得擾動和狀態量,用于控制律設計。完整結構框圖如圖1所示。
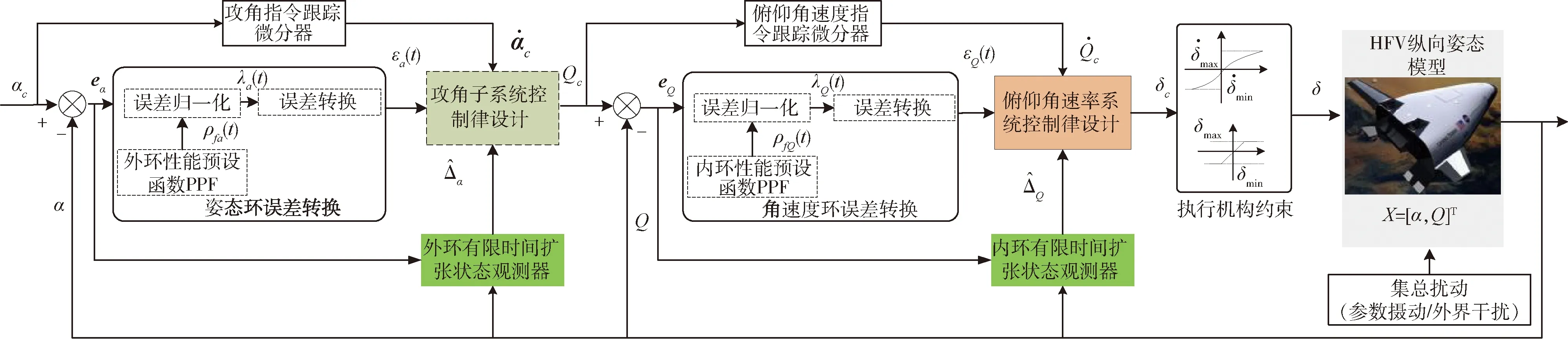
圖1 HFV縱向姿態模型新型性能預設反步控制器結構
2.1 性能預設函數及誤差轉換
一般地,對于性能預設控制而言,第一環節是設計性PPC,其定義如下:
定義1[11]:連續函數ρ(t):+→+為性能預設函數,且滿足如下2個條件:
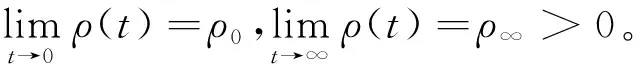
常見的PPC主要包含指數型、正切型和倒數型,如式(5)~(7),均可滿足定義1條件。
ρ(t)=(ρ0-ρ∞)exp(-kρt)+ρ∞
(5)
ρ(t)=coth(ρ0+kρt)-1+ρ∞
(6)
(7)
其中,ρ0>0,ρ∞>0,kρ>0為待設計參數,ρ0代表初始誤差上界,ρ∞代表穩態精度的約束,kρ代表衰減速率,直接影響系統的暫態性能。
根據定義1,本節設計一種有限時間性能預設函數來滿足指令跟蹤誤差的暫態響應和穩態性能,如式(8)。
ρi(t)=
(8)
其中,i=α,Q代表內外環的性能預設函數,且ρi0≥1,ρi∞>0為待設定參數,Ti為設定時間值。相比于傳統PPC,本文設計的性能函數能夠在設定時間點滿足收斂要求,且靈活可調整。
為滿足跟蹤誤差預設性能需求式(4),需要進一步將跟蹤誤差轉化為等價無約束形式:
e(t)=ρ(t)S(ε(t))
(9)
其中,ε(t)為轉換誤差,S(ε(t))為光滑遞增轉換函數,其滿足如下條件
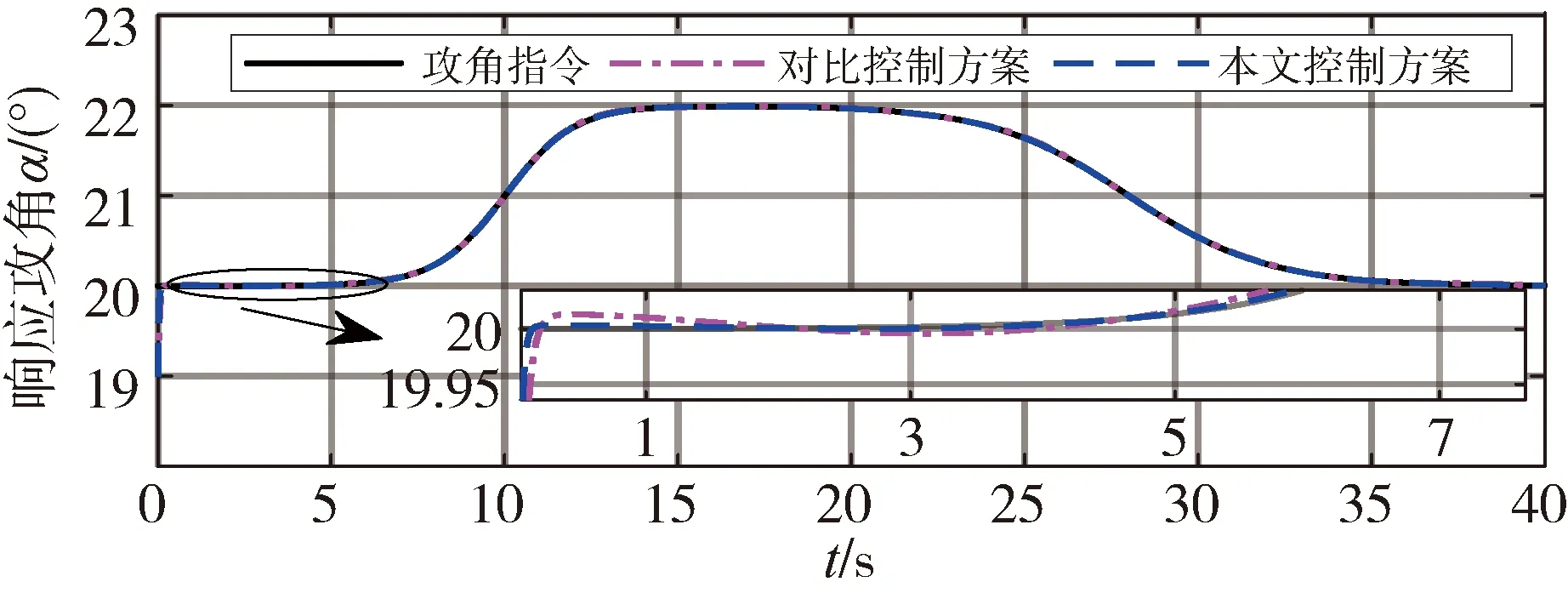
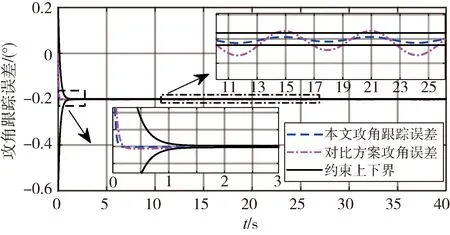
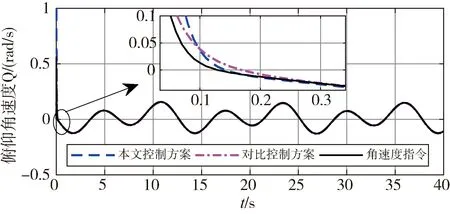
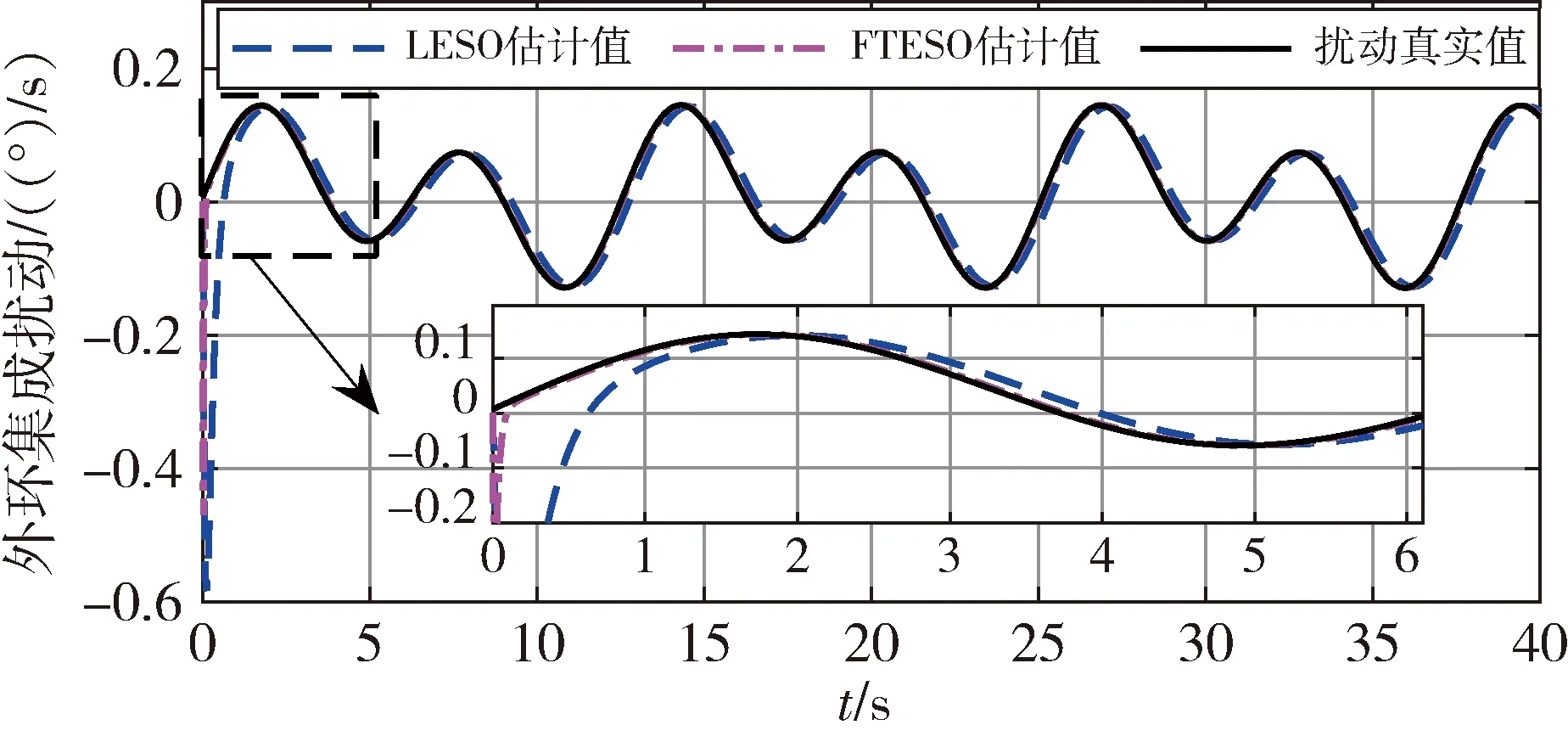
1)-δiL 則可引入指數型轉換函數 (10) 由于S(ε(t))嚴格遞增,轉換誤差可以通過反函數求解為: (11) 其中λi=ei(t)/ρi(t),i=α,Q。 本文基于反步法思想將系統(3)的控制系統設計分為姿態環虛擬控制律設計和角速度環真實控制律設計2個步驟。 步驟1:設計姿態環虛擬控制律 選擇姿態角系統的李雅普諾夫函數 (12) 對式(12)求導 (13) (14) 將式(14)代入到式(13),則有 (15) 步驟2:設計角速度環控制律 選擇姿態角速度系統的李雅普諾夫函數 (16) 對式(16)求導 (17) (18) 將式(18)代入式(17),則有 γQVQ+Ωα+ΩQ≤-γαVα-γQVQ≤0 (19) 由此可得,閉環系統是穩定的。 由式(14)以及式(18)的形式可知,控制律的設計中需要用到指令的微分量,為了防止“計算膨脹”問題,引入跟蹤微分器。受到滑模理論的啟發,引入終端因子來抑制高頻震顫,設計基于Sigmoid函數的微分跟蹤器[12],其形式如式(20)。 (20) 其中tansig(x)=2/(1+exp(-2x))-1,v(t)是輸入信號,x1(t)是跟蹤信號,x2(t)是微分信號,k,λ,l1,l2,p是待設定參數,k=30,λ=10,l1=10,l2=15,p=0.8。 對于性能預設控制器的設計而言,其對于集總擾動的估計精度要求較高,受文獻[13]啟發,設計一種有限時間擴張狀態觀測器,用于對內外環集總擾動的估計。考慮帶有不確定系統 (21) (22) 則針對姿態系統而言,以姿態角系統為例可設計如式(23)的有限時間擴張狀態觀測器。 (23) (24) 角速度環系統擴張狀態觀測器具有相同結構,且限于篇幅,這里不再贅述,穩定性證明略。至此,帶有有限時間擴張狀態觀測器和有限時間跟蹤微分器的高超飛行器縱向姿態性能預設控制器設計完畢。 本節將針對系統式(3),采用控制律式(14)、(18),微分跟蹤器式(20)、不確定估計式(23)進行仿真校驗與分析。驗證飛行器在大攻角再入飛行過程中,存在參數攝動和持續性時變外界干擾的情況下,攻角指令的跟蹤情況。針對攻角子系統和角速度子系統分別設計性能預設函數: (25) ρα0=1,ρα∞=0.005,Tα=1。 (26) ρQ0=2,ρQ∞=0.01,TQ=1。 為校驗本文提出控制方案的有效性,將本文設計的控制律和傳統的反步法控制律(27)對比仿真。 (27) 本文控制器及狀態觀測器參數見表1。 表1 控制器參數 在驗證中,飛行器的不確定性模型及外界持續性擾動設置如下。 對于執行機構而言,通常可用二階慣性環節描述執行機構模型,如式(28),且舵偏約束滿足|δe|≤30°。 (28) 其中,仿真中Tδ=0.1,ωn=1。 將傳統反步法和本文提出的帶有性能預設的控制方案進行對比,圖2為兩種控制方案在表2參數偏差和時變擾動的情況下的質量跟蹤響應曲線,圖3為兩種方案的跟蹤誤差曲線。由圖2~3可知,兩種方案均能夠較好地跟蹤姿態指令,但是在暫態性能(收斂時間)和穩態性能(穩態誤差)上,本文的有限時間性能預設方案表現的更為優異,特別是在穩態精度方面,始終保持在約束的范圍之內,相比于傳統反步法,由于時變擾動的影響,其跟蹤誤差超出了期望的性能邊界(±0.005°)。圖4表示俯仰角度跟蹤效果,其與姿態角子系統有相似結論,這里不再贅述。 表2 飛行器不確定模型 圖2 攻角指令跟蹤(本文控制器與對比控制器仿真) 圖3 攻角跟蹤誤差(本文控制器與對比控制器仿真) 圖4 俯仰角速度指令跟蹤(本文控制器與對比控制器仿真) 為驗證本文設計的有限時間收斂擴張狀態觀測器(FTESO)的有效性,將其和線性擴張狀態觀測器(LESO)相比,以姿態環子系統為例驗證兩者對時變擾動的估計效果。如圖5所示,本文的有限時間擴張狀態觀測器在收斂速度和跟蹤誤差上相比于線性擴張狀態觀測器都有較好的性能。 圖5 姿態環子系統集總擾動估計 針對帶有參數攝動和外界時變擾動的高超聲速飛行器縱向姿態跟蹤控制問題,設計了性能約束控制器。對于跟蹤誤差性能約束,首先設計了固定時間的性能預設函數,相比于傳統的性能預設方案,其能夠保證性能函數在設定的時刻收斂至穩態值,且可根據性能需求和執行機構飽和特性調整設定時刻;針對控制律設計中需要用到的指令的微分信號量,通過引入指令濾波去避免反步法中“計算膨脹”的問題;對于帶有參數攝動和時變擾動的系統,為進一步提升擴張狀態觀測器的性能,設計了有限時間擴張狀態觀測器,其在收斂速度和收斂精度上相比于線性擴張狀態觀測器都有較大的提升。同樣本文的控制方案對執行機構提出了更高的需求,因為其在初始時刻的飽和時間更長。這也是下一步繼續研究的方向,即性能約束條件下的抗飽和控制問題。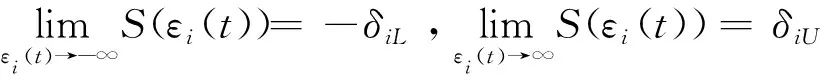
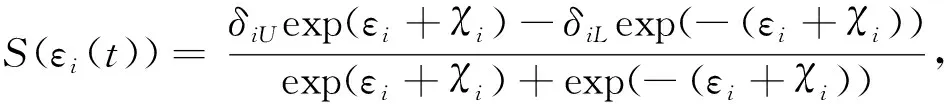
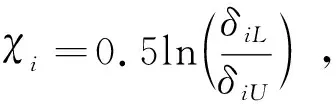
2.2 控制律設計
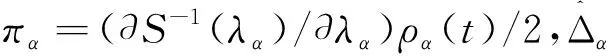
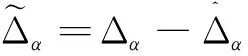
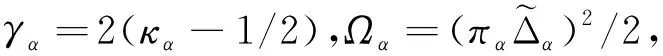
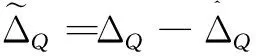
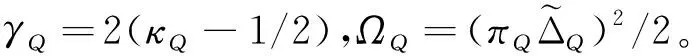
2.3 跟蹤微分器設計
2.4 有限時間擴張狀態觀測器設計
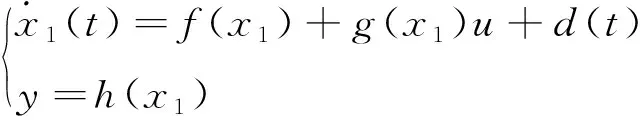
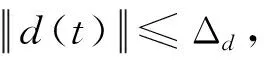
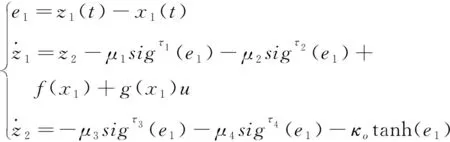
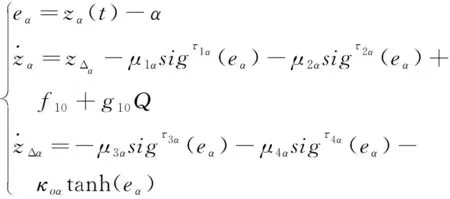
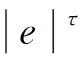
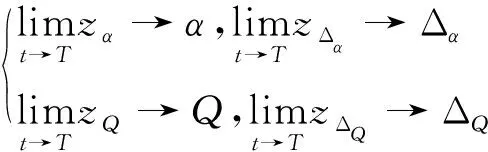
3 仿真校驗
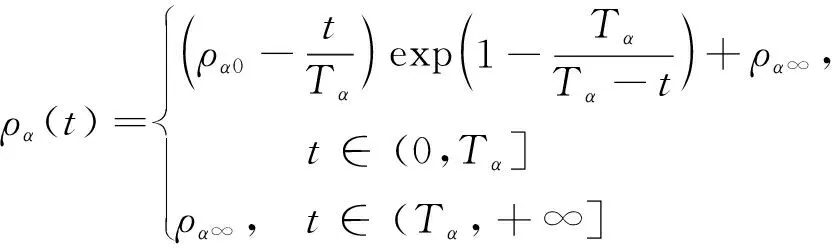
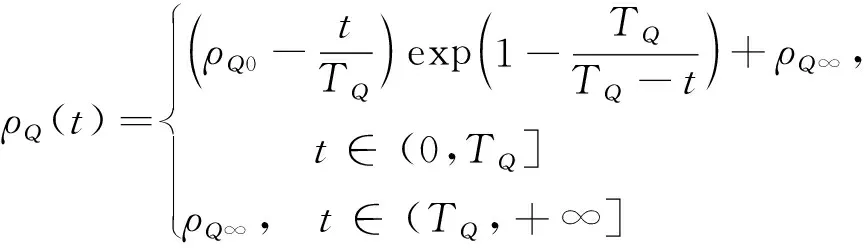


4 結論

