基于點云的空間非合作目標位姿測量方法研究

王昕宇 解永鋒 陳 益 王國輝

1.北京宇航系統工程研究所，北京 100076 2.中國運載火箭技術研究院，北京 100076

0 引言

在軌服務與空間碎片清理是近年來各國關注的焦點[1]，作為其核心技術之一，近距離的空間非合作目標的位姿測量技術也被廣泛研究[2-3]。根據非合作目標模型是否已知，分為已知模型和未知模型，對于已知模型的位姿測量，多采用模板匹配的方式[4-5]，已有大量研究較為成熟，而目前對未知模型的位姿測量的研究則充滿挑戰。

針對模型未知的空間非合作目標位姿測量，常用的解決方案為同時定位和建圖(SLAM)。SLAM最早在機器人領域提出，它指的是：機器人從未知環境的未知地點出發，在運動過程中通過重復觀測到的環境特征定位自身位置和姿態，再根據自身位置構建周圍環境的增量式地圖，從而達到同時定位和地圖構建的目的。

文獻[6]基于SLAM的貝葉斯濾波估計模型,提出了基于視覺的非合作目標的位姿測量方法，實現了對翻滾目標的位姿測量。文獻[7]將經典視覺SLAM算法ORB-SLAM應用于空間非合作目標位姿測量，取得了較好的測量精度。文獻[8]基于共線投影原理創立了雙目視覺的測量模型，融合慣性元件進行組合導航。然而空間光環境復雜且變化劇烈，純視覺方法應用受限。激光雷達作為主動式傳感器，具有較好的光照不變性，被航天器廣泛應用[9]。因此基于激光雷達的位姿測量技術被越來越多的學者重視。

文獻[10]以迭代最近點(ICP)算法為基礎，提出的考慮累積誤差的參數傳遞法進行序列點云配準。文獻[11]分析了非合作目標相對位姿測量中的漂移問題，提出了基于位姿平均的漂移修正方法。文獻[12]將2D-3D多特征融合，求解目標位姿。而文獻[13]則利用位姿圖優化技術，結合閉環檢測，提出了解決累計誤差的完整SLAM框架。

上述提到的點云配準多以Besl等人1992年提出的ICP算法為基礎[14]。但面對非稠密點云，ICP的最近點匹配退化嚴重。文獻[15]中擴展ICP算法整合了點與點和點與面的匹配，拓展了ICP算法適用范圍。但ICP算法每次迭代均需搜索最近點，計算代價較高。文獻[16]提出了NDT算法，通過匹配相鄰幀正態分布柵格，無需迭代搜索最近點，效率更高。

LOAM算法[17]為提高實時性，采用提取邊緣點和平面點匹配的方式，減少了待匹配點數量，同時為了降低運動拖影的干擾，里程計與建圖分為了高頻和低頻2部分。針對低成本的固態激光雷達單線收發、不規則采樣的特點，Livox_LOAM[18]基于LOAM增加了壞點剔除和分段匹配的步驟，提高了里程計的魯棒性。本文在此基礎上，結合空間非合作目標的特點，改進了特征點選擇和位姿迭代優化流程，提出了一種適用于固態激光雷達的空間非合作目標位姿測量方案。

1 特征點提取

1.1 點云采樣

本文主要研究基于固態激光雷達位姿估計，下面以livox公司推出的mid-40激光雷達為例說明點云的采樣特點。

如圖1(a)和(b)所示，激光雷達采用單線激光束在一個圓形平面內掃描，形成一個夾角38.4°的錐形掃描視野。掃描軌跡如圖2所示，形狀類似花瓣。為增加視場內的掃描點覆蓋率，該激光雷達采用了非重復掃描模式，掃描花瓣在不斷旋轉。不過這也使得以搜索最近點為核心的ICP算法效果大打折扣。

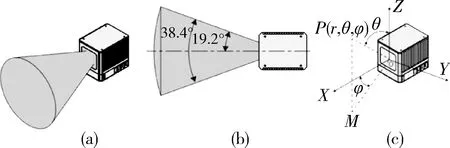
圖1 mid-40激光雷達有效視場范圍

圖2 mid-40激光雷達掃描軌跡

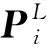
(1)

1.2 邊緣點提取

為了計算每幀點云本地坐標系到世界坐標系的轉換(即位姿)，采用特征點匹配的方式，下面詳細介紹如何針對空間非合作目標提取特征點。

1)轉折點

激光雷達在以花瓣狀軌跡掃描過程中，得到的序列點在遇到物體邊緣時會出現轉折，體現在點云坐標上則為相鄰點之間的微分向量夾角增大。

(2)

式(2)計算出某點Pi和前后兩點之間向量的夾角，以此作為轉折點的判斷標準。但需注意以下2點：

a.剔除視野邊緣點。由圖2知，掃描花瓣在視野中央，軌跡接近直線，而在視野邊緣有近180°轉變，這將影響式(1)的判斷。因此將距x軸15°外的點均不作轉折點判斷。由于一般將目標航天器鎖定在視野中央，因此不會明顯降低特征點數量。

b.距離雷達近優先。圖3(a)中，A、B兩點均可由式(1)判斷為轉折點，而顯然點A是由于點B的遮擋而轉折，更換視角后，點A將不再是邊緣點，因此在檢測到轉折點后需判斷當前點與下一個點哪一個距離雷達更近，將更近點選為邊緣點。

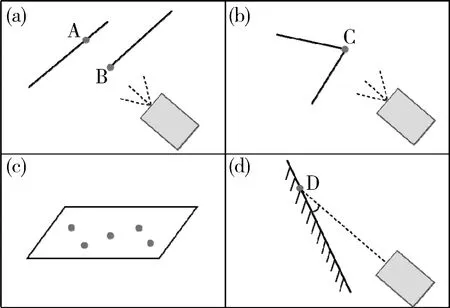
圖3 激光雷達采樣點示例

2)斷點

在空間環境中，如果激光束沒有照射到目標航天器上，則意味著無法被反射回雷達，測量結果為無窮遠。而激光雷達掃描中從航天器到宇宙空間過程中必然經過邊緣點，本文稱之為斷點，如圖3(b)所示。因此如果某點的一側為無窮遠，而該點在另一側連續，則可以為是斷點。

1.3 平面點提取

判斷某一點是否在一個平面上，很難通過單線掃描的序列點完成，本文借鑒主成分分析算法，提出一種單線掃描下的平面點提取方案，步驟如下：

a.選擇待判斷點附近一定距離內點(如5 cm內)，假設為k個，由圖2可知，0.1s時掃描覆蓋率已經較高，因此k個點不會來自共線的連續掃描。

b.計算k個點的均值與協方差矩陣，并計算協方差矩陣的特征值與特征向量。

c.根據主成分分析理論，協方差矩陣的特征值越小，在該特征方向的分布越集中，近似壓縮在一個平面上，如圖3 (c)所示。因此將最小特征值是次小的三分之一作為k個點是否組成平面的依據，并據此判斷該點是否在平面上，即平面點。

然而，值得注意的是，圖3(d)中平面與激光束夾角很小，此時激光束會在平面上照射出拉長的光斑，測距精度將顯著下降，因此對該種情況的平面點進行剔除。

2 迭代位姿優化

為解算出激光雷達繞空間目標移動過程中的位姿變化，需要計算每一幀本地坐標系下的點云相對于第一幀的世界坐標系之間的旋轉和平移，即(Ri,Ti)。本文采用上一節介紹的算法提取每一幀的特征點，將其與之前所有幀的特征點進行匹配，迭代優化Ri與Ti使得匹配誤差最小。

2.1 特征點匹配

由于固態激光雷達的不重復掃描特點，直接點與點的匹配很難實現，因此采用邊緣特征點與直線和平面特征點與平面的匹配方式。

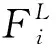
為提高迭代效率，設置合適位姿初值，本文以i-1與i-2幀間位姿變化預估第i幀位姿，在齊次坐標系下表示為：

(3)

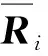
1)點與線

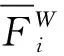
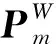
(4)

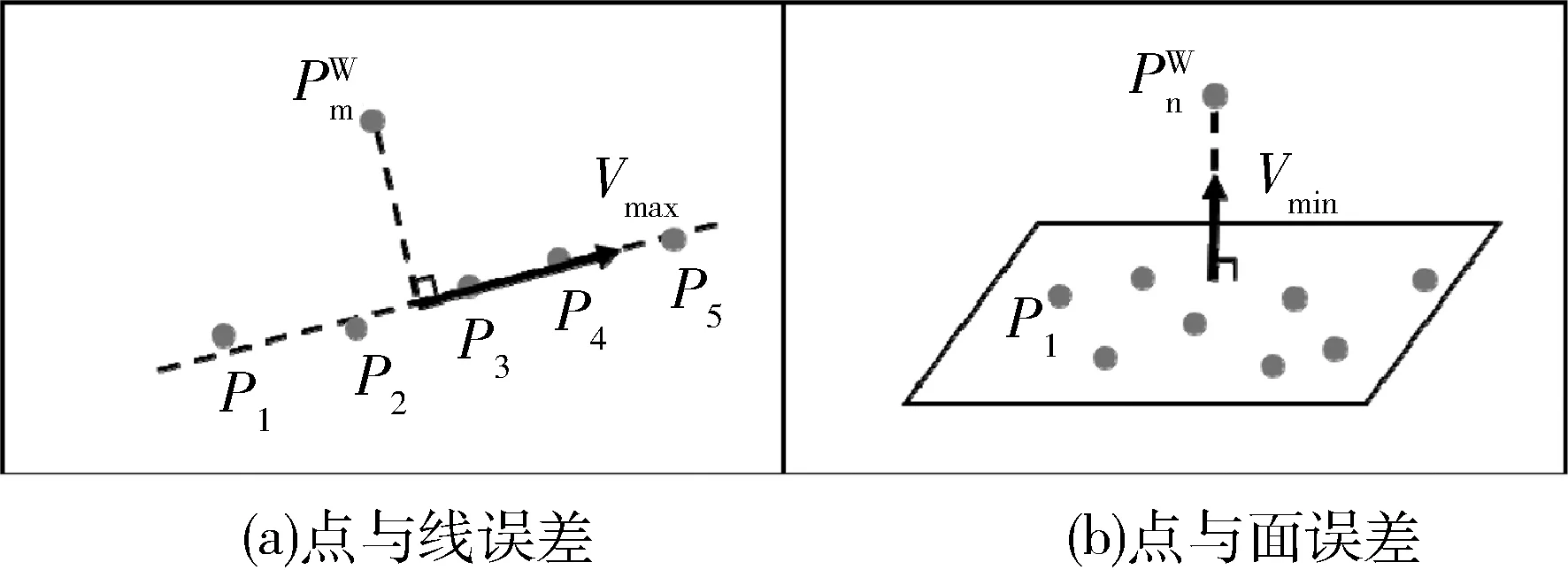
圖4 匹配誤差示意圖

2)點與面

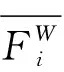
(5)

2.2 迭代優化

2.1節分別計算出點與線、點與面匹配的誤差，一幀點云總的誤差為

(6)

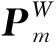
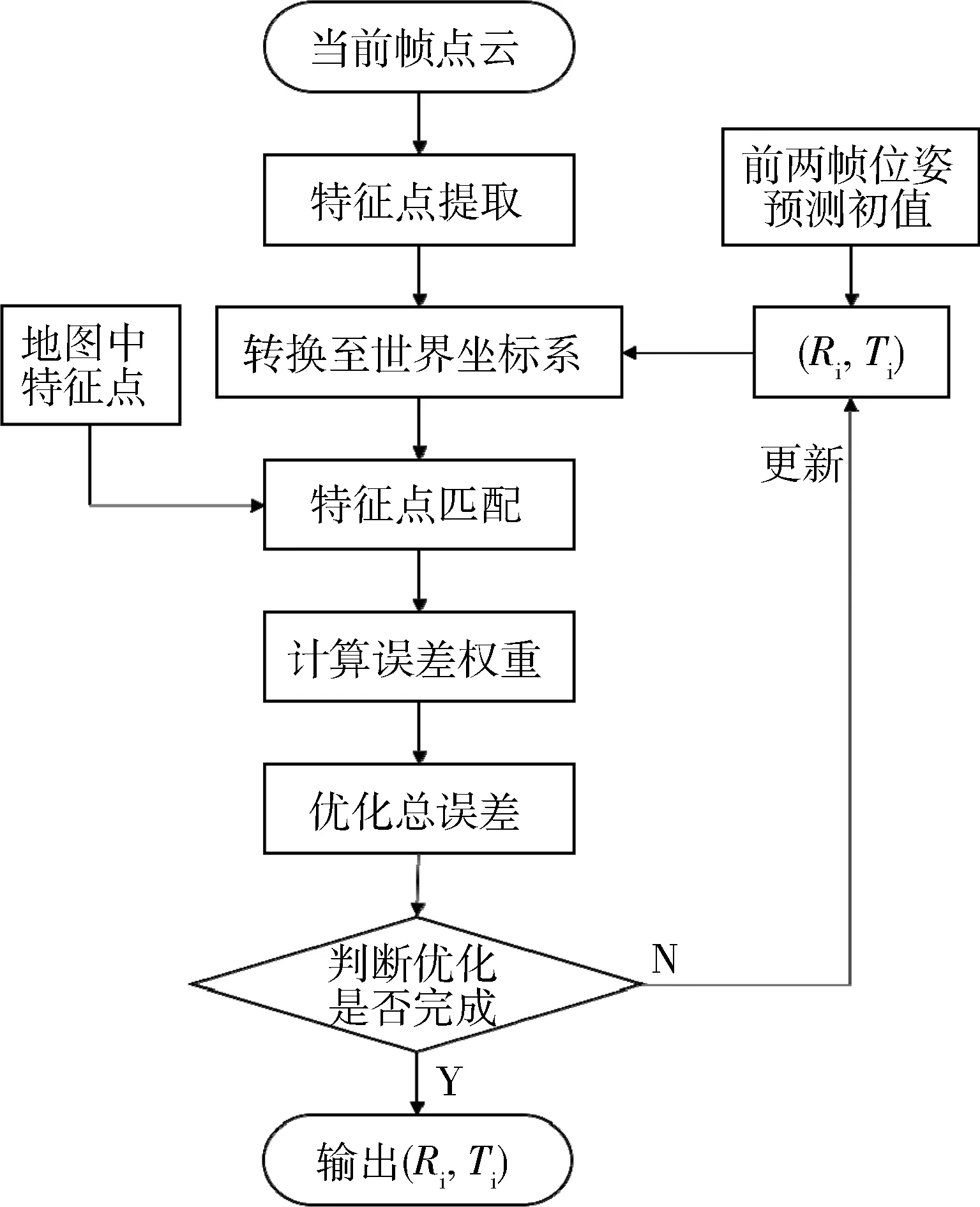
圖5 位姿優化算法流程

圖5的算法流程中，特征點匹配完成后，增加一步誤差加權：

(7)

式中：d為誤差值，ρ(d)為加權系數，h為給定參數，設為0.01m。經過該步驟，匹配誤差較大項在總誤差中占比會下降，減少了離群點對最終結果的影響。

算法最后判斷優化是否結束，若前后兩輪優化結果差別很小或達到最大輪次，則結束優化，輸出結果。否則算法將以最新的估計位姿(Ri,Ti)更新特征點在世界坐標系中的坐標，迭代優化。

2.3 運動補償

固態激光雷達單線掃描特點，導致同一幀點云并非同時采樣獲得，而是在一個時間段內依次采樣，而采樣時雷達自身在不斷運動，由此產生運動拖影，本文采用線性插值方法進行運動補償。

以(Ri,Ti)為第i幀最后一個采樣點的雷達位姿，則第i幀最后一點(時刻ti)到第i-1幀最后一點(時刻ti-1)之間的位姿變換為：

(8)

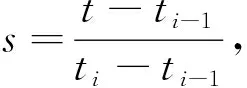
(9)

式中：旋轉角θ可由ΔRi的跡計算，而旋轉向量經ΔRi的旋轉不會改變，所以旋轉向量n為ΔRi的特征值為1的特征向量。旋轉角線性插值后使用羅德里格斯公式[19]轉換回矩陣：

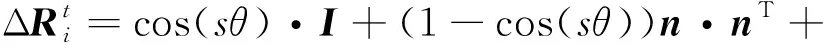
(10)

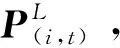
(11)

3 實驗校驗

為了校驗所提算法的有效性，本文對氣浮臺半實物實驗所得數據進行處理。

3.1 實驗條件

為模擬太空中追蹤航天器與目標航天器的真實相對運動情況，采用了氣浮模擬器繞飛目標模擬器的方式進行演示實驗，如圖6所示。

圖6 實驗裝置

追蹤模擬器距離目標模擬器2m，以1.5(°)/s的角速度繞飛。追蹤模擬器上安裝有光學追蹤器，使用OptiTrack外部光學測量系統測量位姿，將其測量值作為算法參考的位姿真值。

3.2 結果及分析

追蹤模擬器繞飛目標模擬器一周后，根據計算得到的每一幀點云位姿，將點云坐標統一變換到世界坐標系下，得到圖7的目標三維模型。

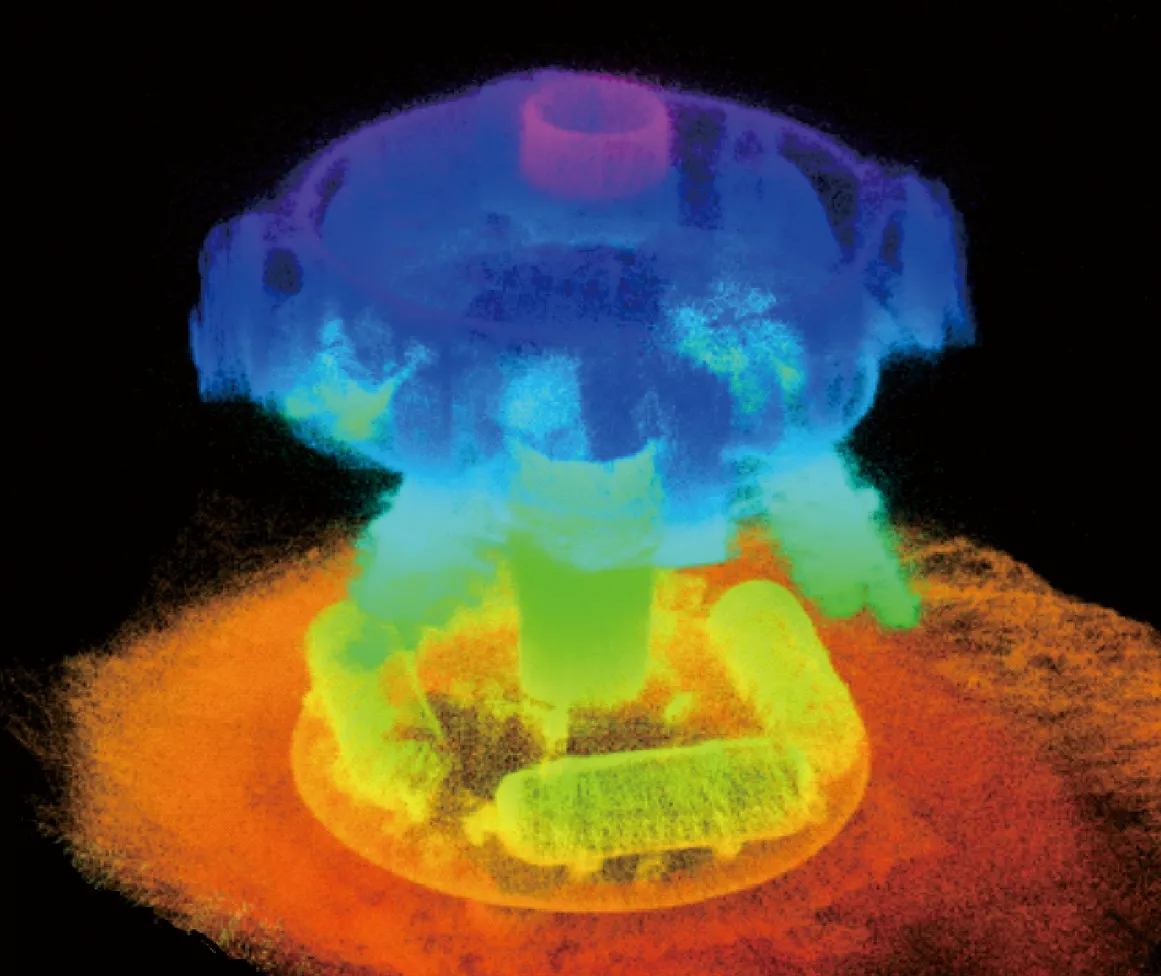
圖7 目標模擬器三維模型

圖8為追蹤模擬器的繞飛軌跡誤差熱力圖，圖9展示了三軸坐標系下激光雷達測量軌跡與真實軌跡的誤差，圖中可知，兩條軌跡基本吻合。圖10量化統計了測量軌跡與真實軌跡的累積誤差，即圖中APE。絕對累積誤差并未持續增加而是上下震蕩，表明算法中每一幀點云均和全局地圖匹配的設計，有一定的回環修正能力。

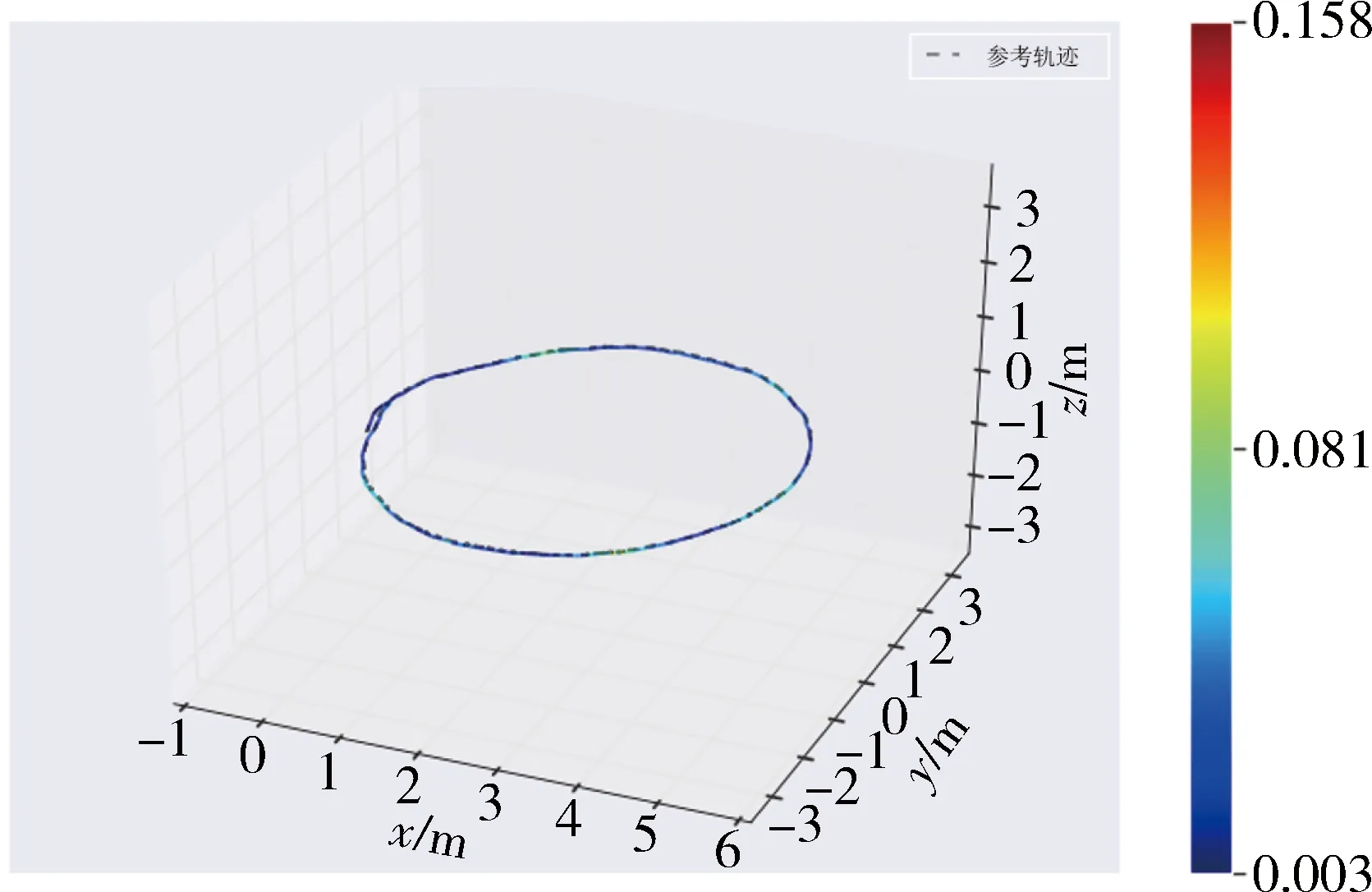
圖8 測量軌跡誤差熱力圖

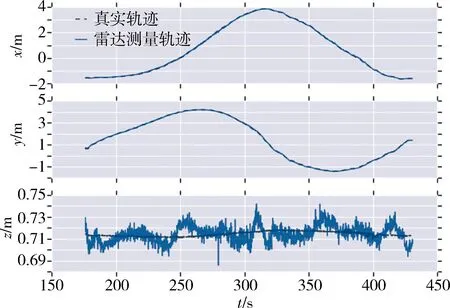
圖9 三軸坐標系下軌跡誤差

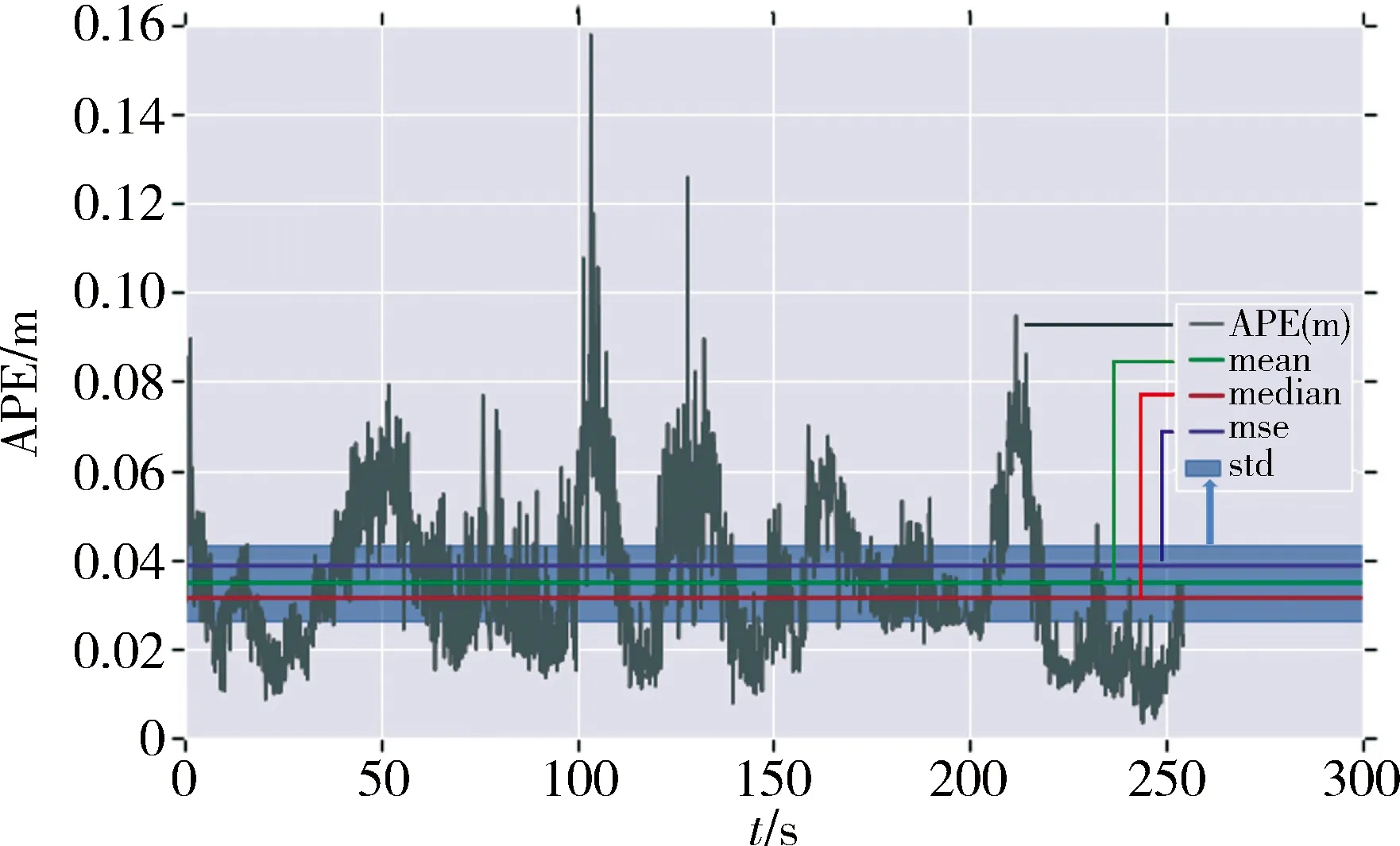
圖10 絕對軌跡誤差信息

本文將所提出算法與Livox公司開源算法對比，結果如表1所示。在最大誤差相似情況下，本文算法的軌跡均值誤差與均方根誤差均明顯低于對照算法，能夠滿足航天器相對位姿測量的要求。

表1 算法軌跡誤差對比

4 結論

為測量模型未知的空間非合作目標位姿，本文提出了基于固態激光雷達的測量方法。該方法針對空間目標提取特征點，與全局地圖匹配后迭代優化位姿，克服了固態激光雷達不規則采樣的缺點，在半實物實驗中準確測量了相對位姿變化，證明了方法的有效性。