基于廣義除法下非線性模糊差分方程的動力學行為研究*

王貴英， 張千宏

1. 河池學院， 數理學院， 廣西 河池 546300； 2. 貴州財經大學 數學統計學院， 貴陽 550025

模糊差分方程是指系數或初值為模糊數的差分方程， 模糊差分方程的出現， 解決了差分方程無法準確建模的問題， 因此， 模糊差分方程在許多科學研究領域有著舉足輕重的地位．

針對于模糊差分方程的研究， 大多數學者更傾向于研究只具備模糊數乘法、 加法的模糊差分方程[1-5]． 文獻[1]研究了一階模糊差分方程

xn+1=ωxn+qn=0，1，2，…

其中：xn是模糊序列；ω，p，x0是正模糊數．

文獻[2]研究了模糊差分方程

xn+1=Axn+Bn=0，1，2，…

正解的存在性、 有界性以及正解的漸近表現， 其中A，B，x0是正模糊數．

文獻[6-12]研究帶除法的模糊差分方程． 文獻[6]通過對模糊數使用Zadeh擴展原則， 研究了模糊Riccati差分方程

正解存在性與唯一性等相關問題， 其中A，B，x0是正模糊數．

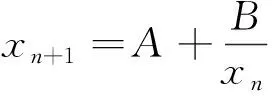
(1)

的全局漸近行為， 其中m∈N+，A，B以及初始條件x-m， …，x0都為正模糊數．

1 相關引理及定義

1)u是正規的， 即存在x為實數， 使得u(x)=1；

2)u是模糊凸的， 即對所有的t∈[0， 1]，x1，x2∈R有

u(tx1+(1-t)x2)≥min{u(x1)，u(x2)}

3)u是上半連續的；

對于所有的α∈(0， 1]，u的α-截集表示為[u]α={x∈R：u(x)≥α}．

定義2[11]設u，v是正模糊數， 則u，v的α-截集表示為[u]α=[ul，α，ur，α]， [v]α=[vl，α，vr，α]，α∈(0， 1]， 且

定義u的模為

u，v之間的距離為D(u，v)， 其中

[g(u，v，ω)]α=g([u]α， [v]α， [ω]α)

定義3[11]令u，v是模糊數，α-截集為[u]α=[ul，α，ur，α]， [v]α=[vl，α，vr，α]， 0?[v]α， 對于?α∈(0， 1]， 定義÷g(g-除法)： 存在一個模糊數ω， 且[ω]α=[ωl，α，ωr，α]， 使得

ω=u÷gv

即是

(2)

易知， 任意的模糊數u， 當u定義在g-除法上時， 有u÷gu=1， 當u定義在Zadeh擴展原則上時，u÷gu≠1．

引理2[11]令u，v都是模糊數， 如果ω=u÷gv存在， 則有以下兩種情況．

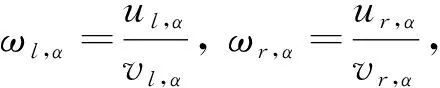
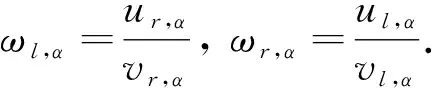
引理3[13]令u，v，ω都是正模糊數， ?α∈(0， 1]， 如果ω=u÷gv滿足引理2中的1)， 則

(3)

如果ω=u÷gv滿足引理2中2)， 則

(4)

因此有

(5)

注因為|ur，αvr，α-ul，αvl，α|≥|ur，αvl，α-ul，αvr，α|， 由(3)，(4)，(5)式可知， 運用g-除法優于Zadeh擴展原則．

引理4[13]考慮差分方程

(6)

其中：n=0，1，2，…，m；m∈N+，α，β，yi(i=-m，…，-1，0)都是正實數． 則

1) 方程

λ2-αλ-β=0

(7)

有一正一負的兩個實特征根λ1，λ2．

定義4[11]令y=max{λ1，λ2}， 其中λi(i=1，2)是(7)式的特征根， 則稱y為(6)式的唯一平衡點．

引理5[13]考慮差分方程系統

(8)

其中m為正整數，α，β，μ，ν，yi，zi(i=-m，…，-1，0)都是正實數． 則有

1) 方程

μλ2+(ν-αμ-β)λ-αν=0 (或αγ2+(β-μα-ν)γ-μβ=0)

(9)

有兩個一正一負的實特征根λ1，λ2(或γ1，γ2)．

2) 方程(9)的每一個正解， 都有

定義5[4]令y=max{λ1，λ2}，z=max{γ1，γ2}， 其中λi，γi(i=1，2)是方程(9)的特征根， 則稱(y，z)是方程(8)的唯一解．

定義6[4]設{xn}是正模糊數數列， 若存在正實數P，Q， 使得

supp(xn)?[P，Q]n=1，2，…

則稱(xn)是有界且持久的．

定義7[11]如果正模糊數數列(xn)滿足模糊差分方程(1)， 則稱xn是方程(1)的正解． 如果x滿足方程

則稱x是模糊差分方程(1)的平衡點．

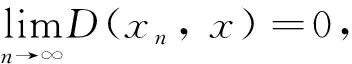
2 主要結論

主要對兩個模糊數運用g-除法， 討論高階非線性模糊差分方程

(10)

解的唯一性以及全局漸進行為． 其中m為正整數，A，B，xi(i=-m，…，0)都是正模糊數．

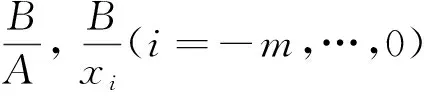
證定理的證明與文獻[15]中的命題3.1的證明類似， 這里省略定理1的證明．

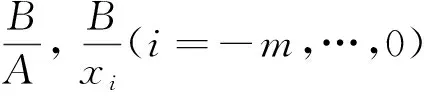
(11)

成立時， (10)式存在唯一解xn．

注定理2的證明方法與定理1基本一致．

定理3考慮差分方程(6)， 存在一個正常數θ>0， 當n≥1時， 有

(12)

證由(6)式可知， 對于?α≥1， 都有yn≥α． 當n→∞時， 則有

其中

所以有

同理可得

因此， 對于?n≥m， 都有

yn≤θ

(13)

其中

由(6)式及(13)式， 可得

(14)

定理證明完畢．

定理4考慮方程(10)， 其中A，B以及初始條件xi(i=-m，…，0)都是正模糊數， 當方程(10)中除法滿足引理2中的1)時， 方程(10)的每一個正解xn都是有界持久的．

證因為A，B以及初始條件xi(i=-m，…，0)都是正模糊數， 所以存在Mi，Ni(i=0， 1， 2， 3， …，m)使得

(15)

令xn是方程(10)中滿足引理2中1)情形時的正解， 由定理3及方程(10)， 則有

(16)

其中

聯系(15)式， 可得

由(15)，(16)式可得到Ln，α≥P， 其中

同理得

因此， 對于n≥1， 有

也即是

由定義6知，xn是有界持久的． 證畢．

定理5考慮差分方程系統

(17)

其中m為正整數，α，β，μ，ν，yi，zi(i=-m， …， 0)都是正實數， 當不等式組

(18)

成立時， 存在正常數K1，K2，C1，C2， 使得

K1≤yn≤K2，C1≤zn≤C2

證由引理5可知， 系統(17)存在唯一正解(yn，zn)， 且易得出yn≥α，zn≥μ， 當n→∞時， 由(17)式有

所以有

(19)

同理可得

(20)

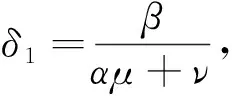
yn≤K2?n≥1

(21)

其中

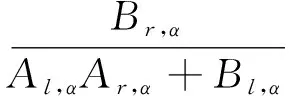
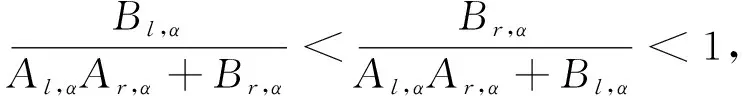
(22)

對于Ln，α，Rn，α， 由定理5以及(22)式有

其中

由(15)式有

再令

即P≤Ln，α， 同理可得Q≤Rn，α， 其中

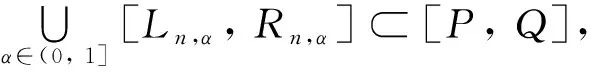
定理7當方程(10)中的g-除法滿足引理2中1)時， 則

1) 方程(10)存在唯一平衡點x；

2) 當n→∞時， 方程(10)每一個正解xn都趨于唯一平衡點x．

證由引理2中1)與(10)式可得

(23)

(24)

由引理4、 (23)式和(24)式可知

(25)

由(15)，(25)式有

(26)

(27)

并且

(28)

也即xn→x． 定理證畢．

定理8當方程(10)中的g-除法滿足定理2中2)情形時， 則有以下結論成立

1) 方程(10)存在唯一平衡點x；

2) 方程(10)每一個正解xn都趨近于唯一平衡點x．

注定理8證明與定理7相似， 此處省略定理8的證明．

4 數值例子

例1考慮四階模糊差分方程

(29)

其中：A，B以及初值xi(i=-3， -2， -1， 0)如下

取α-截集， 有

[A]α=[4+2α， 8-2α]， [B]α=[5+5α， 15-5α]， [x0]α=[6+2α， 10-2α]

[x-1]α=[2+α， 4-α]， [x-2]α=[3+α， 5-α]， [x-3]α=[4+α， 6-α]，α∈(0， 1]

(30)

由定理4可知， 方程(29)的解都是有界持久的， 且存在唯一平衡點x， 當n→∞時， 方程(29)的每一個正解xn都收斂于唯一平衡點x(如圖1-4)．

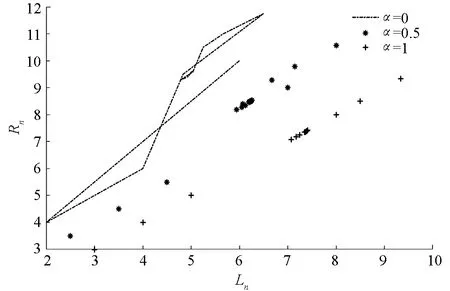
圖1 系統(30)動力學行為

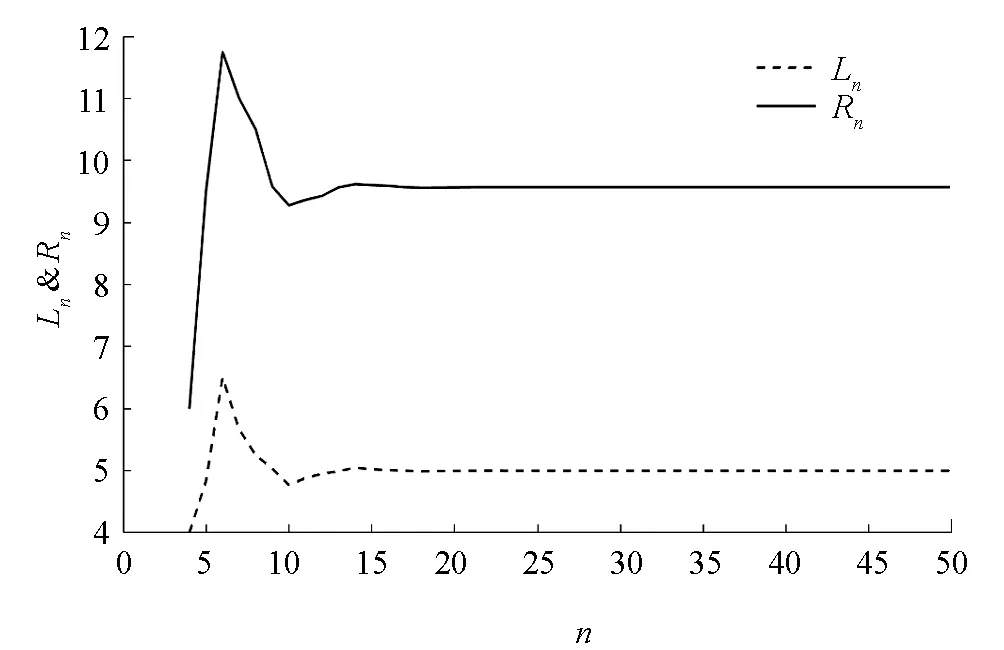
圖2 α=0時， 系統(30)的解

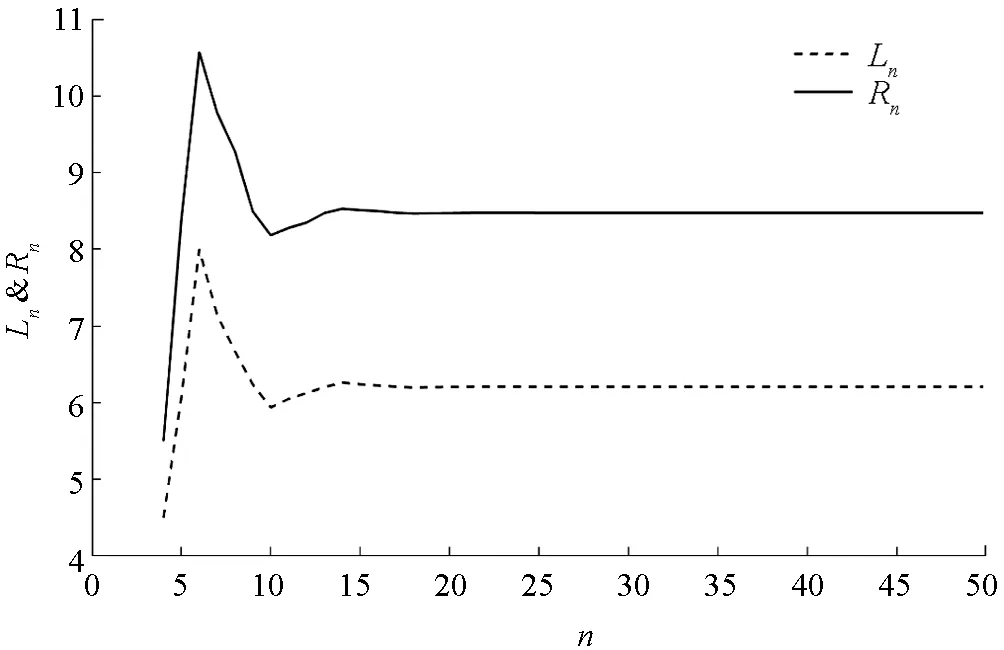
圖3 α=0.5時， 系統(30)的解

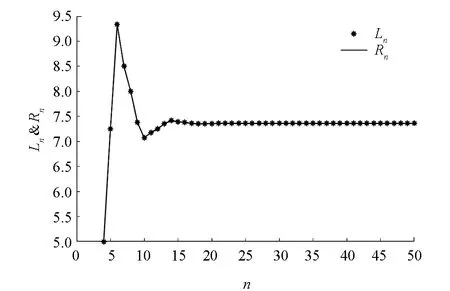
圖4 α=1時， 系統(30)的解

例2考慮三階模糊差分方程

(31)

其中A，B以及初值xi(i=-2， -1， 0)如下

所以有

[A]α=[1+α， 3-α]， [B]α=[2+α， 4-α]， [x0]α=[3+3α， 9-3α]

[x-1]α=[9+3α， 15-3α]， [x-2]α=[15+3α， 21-3α]，α∈(0， 1]

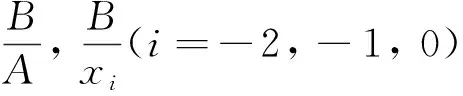
因此

(32)

圖5 系統(32)的動力學行為

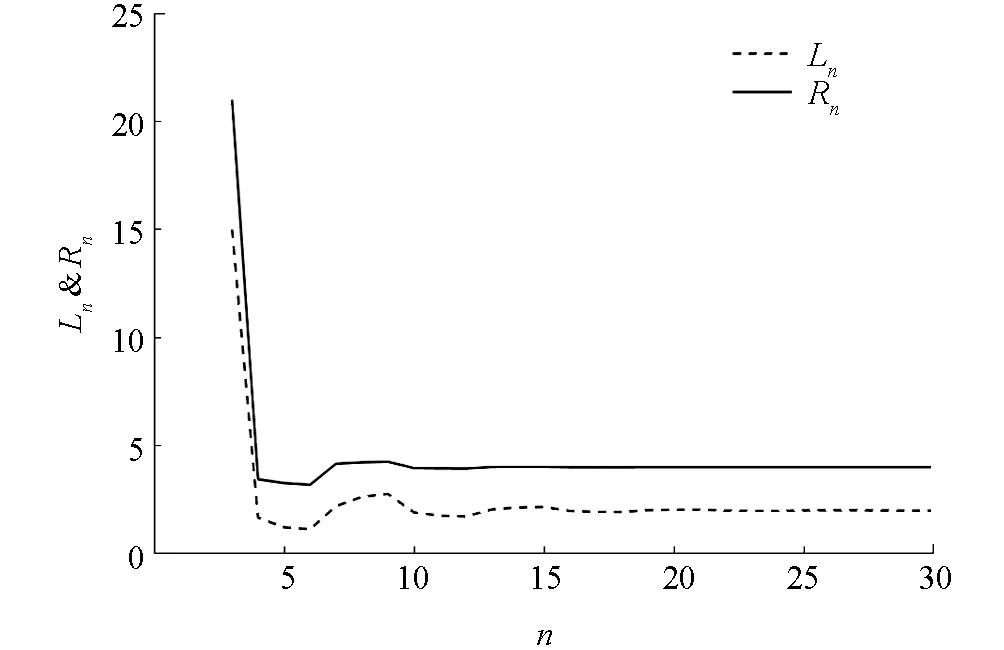
圖6 α=0時， 系統(32)的解

圖7 α=0.5時， 系統(32)的解

圖8 α=1時， 系統(32)的解

5 總結

本文主要運用g-除法， 研究在兩種情況下高階非線性模糊差分方程(1)的正解存在性以及唯一性， 有界性以及持久性以及解的漸近行為． 結論得出， 方程(10)的每一個正解都趨近于唯一平衡點， 最后分別給出三階和四階符合條件的數值例子， 更好驗證結論的有效性．