城軌道岔轉轍器的理論計算方法探討

田苗盛

(中國鐵路設計集團有限公司,天津 300142)

1 概述

道岔是軌道交通必不可少的重要設備。城軌道岔的號數較低,正線一般采用9號道岔,車場線一般采用7號道岔。城軌道岔的顯著特點是直向、側向設計允許通過速度較低,且對乘客的舒適性影響較大。城軌道岔由轉轍器和轍叉兩部分構成,目前各大城市所用道岔均不相同,其不同點主要體現在轉轍器部分。已有學者進行相關研究,劉道通等對9號直尖軌道岔參數及構造進行論述[1];劉婷林等對50kg/m鋼軌9號道岔轉轍器尖軌活接頭進行優化設計[2];楊亮對7號道岔的尖軌跟端活接頭,尖軌寬度及轍叉材質等方面進行優化[3];全順喜對道岔轉轍器平面線形進行研究[4]。隨著制造工藝及技術水平的提高,轉轍器的理論計算方法同樣需要進行改進。因此,針對轉轍器各零部件的理論計算方法進行研究很有必要。

2 道岔設計內容

道岔設計內容主要包括總圖設計和結構設計。道岔總圖在設計過程中需要結合車輛核對舒適性參數,部分參數如下。

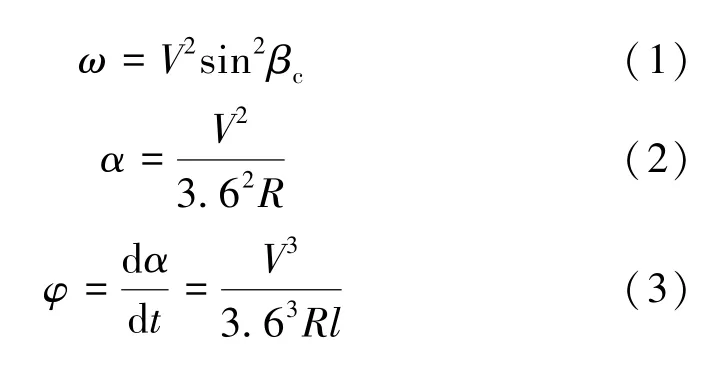
式中,ω為動能損失;Ω為動能損失;α為未被平衡的離心加速度;φ為未被平衡的離心加速度增量;V為列車運行的速度;βc為撞擊部位的沖擊角;R為導曲線股道中心半徑;l為車輛全軸距。

規范給出參數的取值范圍,ω0≤0.65km2/h2;

α0≤0.56m/s2;φ0≤0.5m/s2[5]。

在總圖設計完成之后,應依據總圖進行結構設計。式(1)～式(3)所述參數直接影響道岔結構的設計工作,以下結合道岔轉轍器的結構設計計算方法進行討論。

3 轉轍器的理論計算方法

道岔轉轍器的結構設計依據是道岔總圖,在道岔總圖中,已經對轉轍器線形進行相關設計。……