環環設問把握本質 步步探究提升素養
——“無刻度直尺網格作圖——垂直平分線”的課堂實錄與思考

湖北省武漢市吳家山第二中學 李幽蘭 尹姝暢

湖北省武漢市吳家山第三中學 萬建光

1 引言

我國著名數學家華羅庚曾說過：“形缺數時難入微，數缺形時少直觀.”幾何直觀可以幫助學生直觀地理解數學，在整個數學學習過程中都發揮著重要作用.無刻度直尺網格作圖題，就是只能用無刻度的直尺在網格中取點、畫直線、射線或線段，畫出符合題目要求的圖形.隨著素質教育的不斷深入以及試題改革的不斷發展，無刻度直尺作圖題逐漸受到命題人關注，在近幾年的中考試題中頻頻出現.

2 內容與地位

無刻度直尺網格作圖這類題目需要學生具備較強的幾何知識的思維能力和綜合運用能力，既考查學生的幾何直觀、推理能力，又考查學生的應用能力和創新能力，促進學生的核心素養的形成[1].

《義務教育數學課程標準》中明確要求，學生能用尺規作出一條線段的垂直平分線，過一點作已知直線的垂線.本節課是基于人教版八年級數學上冊前三章內容的期中復習專題課，將三角形全等的性質與判定、線段垂直平分線的性質與判定、等腰三角形的性質等知識有機融合，探究作線段垂直平分線的基本方法，培養學生識圖與作圖的能力.

3 教學目標與重難點

本節課的教學目標：

(1)掌握運用無刻度直尺作已知線段垂直平分線的基本方法；

(2)解決線段垂直平分線的作圖問題，增強學生幾何直觀及操作的能力；

(3)滲透轉化的數學思想，提升學生幾何綜合素養.

本節課的重難點：掌握運用無刻度直尺作已知線段垂直平分線的基本方法.

4 課堂實錄

4.1 導思求學

師：同學們，今天這節課我們一起來學習“無刻度直尺網格作圖——垂直平分線”，首先回顧一下線段垂直平分線的定義.

生1：經過線段中點并且垂直于這條線段的直線，叫做這條線段的垂直平分線.

師：回答正確.作線段的垂直平分線，必須抓住兩個要點：中點和垂直.“磨刀不誤砍柴工”，在學習如何作線段垂直平分線之前，我們先來弄清楚怎樣在網格中作出線段的中點和垂線.

基本作圖1：作線段的中點.

在正方形網格中，有如圖所示(圖1、圖2)的線段AB，請用無刻度直尺作出線段AB的中點C.僅用無刻度的直尺在給定網格中完成畫圖，畫圖過程用虛線表示，畫圖結果用實線表示.

圖1

圖2

學生發現作法，教師點評：根據格線的平行或垂直關系取格點構造“8字形”三角形全等是網格中作線段中點的基本方法.構造8字形的取點方式不唯一，作線段中點的方法也不唯一.

基本作圖2：過已知點作線段的垂線.

請在圖3、圖4中用無刻度直尺分別過點B和點C作BD⊥AB，CE⊥AB.

圖3

圖4

師：如圖3,當線段AB在格線上時，點B所在的豎格線上的點都滿足BD⊥AB，點C所在的豎格線上的點都滿足CE⊥AB.如圖4,當線段AB不在格線上時，如何作垂線呢？在作圖前，我們先來思考一下，如圖5，如果將矩形AGBF繞點B逆時針旋轉90°，得到矩形DMBC，則旋轉前后的對角線AB和BD有什么位置關系？為什么？

圖5

師生活動：學生觀察思考，易說明AB⊥BD，直線BD即為過點B所求的垂線.

追問：那么如何過線段外格點C作CE⊥AB？

生2：可以將剛才得到的線段BD平移，平移后的線段還是與AB垂直，點B向下移2格是點C，所以點D向下移2格就是點E，連接CE，直線CE即為所求AB的垂線CE.

師：非常精彩！我們觀察到線段AB“橫2格，縱3格”，它的垂直線段BD和CE都是“橫3格，縱2格”，所以我們可以歸納得出：線段“橫a縱b”的垂直線段為線段“橫b縱a”.

設計意圖：通過兩個基本作圖，學生掌握網格中線段在格線上、線段不在格線上的中點作法和過一點作其垂線的基本方法，為下一環節作線段垂直平分線做好準備.

4.2 共研釋疑

問題1請作出線段AB的垂直平分線CD.(見圖1)

生3：圖6可以直接取AB的中點C，點C所在的豎格線即為線段AB的垂直平分線.

圖6

師：回答非常棒！抓住垂直平分線定義中的兩個關鍵要素：中點和垂直.這就是我們在網格中作線段垂直平分線的基本方法和基本思路.方法(1)：取中點作垂線.

追問：對于圖7，線段AB的長度為5個單位長度，它的垂直平分線怎么畫呢？中點怎么取？垂線怎么畫？

圖7

生4：(展示作圖)可以構造8字形全等三角形來取中點，作垂線的話可以同樣方式再取一個滿足條件的點.

師：活學活用不錯哦！既然我們可以取出垂直平分線上(與線段兩端點距離相等)的1個點，那么我們也可以取出2個這樣的點，而且不限于在格線上，在方格內可以通過連小正方形對角線的方式找到其中心(如圖8)，因此得到方法(2)：取2個到線段端點距離相等的點再連線.

圖8

問題2當線段AB不在格線上，如何作它的垂直平分線？

師：我們可以很容易畫出線段的中點和垂線，有什么方法使線段的垂線經過中點呢？

師生活動：學生小組討論，交流作法，然后展示(如圖9-1,9-2).

圖9-1

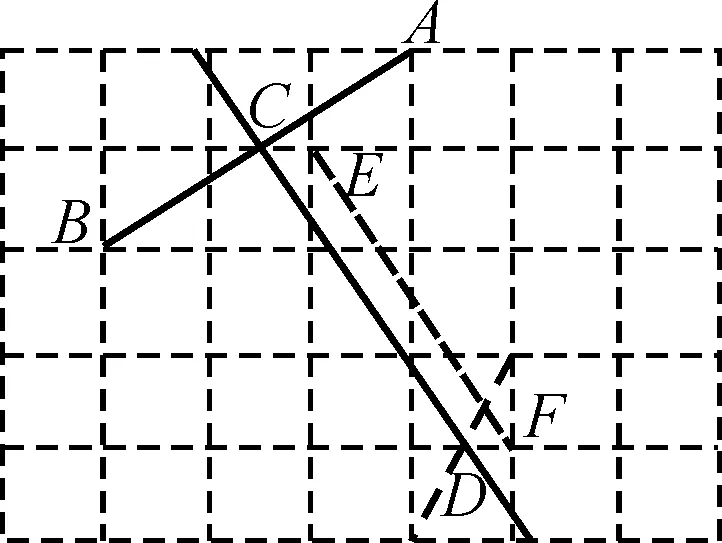
圖9-2

教師對學生的作法給予正面評價，指出需注意的問題，引導學生比較這幾種方法，總結出作線段垂直平分線的方法(3)：平移已知垂線經過中點.注意找到線段平移前后對應點的對應關系.

問題3如果改變網格的行列數，又怎樣作線段AB的垂直平分線呢？

師生活動：學生獨立思考，交流討論，展示作法.引導學生聯系前面總結的方法，作出線段AB的一條垂線EF，然后平移這條垂線經過中點C，得到所要求的垂直平分線，如圖10-1;進一步引導學生將△ACE繞點C順時針旋轉90°得到△DCF，確定點D的位置，連CD即可，如圖10-2.這就是方法(4)：旋轉三角形作垂線.

圖10-1

圖10-2

設計意圖：通過問題1，2，3的作圖，學生掌握在網格中用無刻度直尺作線段垂直平分線的基本方法，即主要是平移和旋轉這兩大圖形變換的應用.其中圖10-1和圖10-2可轉化為基本作圖，滲透化歸的思想方法.學生在動手實踐和小組交流中感知無刻度直尺作圖的解題特點，經歷知識和方法的生成過程，從而探究發現和總結方法.

4.3 拓展應用

(2021武漢中考第20題)如圖11是由小正方形組成的5×7網格，每個小正方形的頂點叫做格點，矩形ABCD的四個頂點都是格點．僅用無刻度的直尺在給定網格中完成畫圖，畫圖過程用虛線表示.

圖11

在圖12中，先畫△BCD的高CG，再在邊AB上畫點H，使BH=DH.

圖12

師生活動：學生交流作法，展示作法，如圖12.教師引導學生明確解題思路，對學生的作法給予肯定評價，掌聲鼓勵，并做相關補充.

設計意圖：這道題目是2021年武漢中考第20題第(2)問，雖然有一定難度，但通過本節課內容的鋪墊和學習后，學生較易讀懂題目的意圖，明確解題思路，攻克中考題目，體會成功的喜悅，感受“學習有用的數學”.

4.4 總結歸納

師：通過本節課的學習，簡單談談你的收獲.

師生活動：學生分享收獲，學生之間互相補充，教師積極引導、評價.

設計意圖：回顧這節課學習的知識和方法，加深對所學知識的理解，培養學生善于總結的良好習慣.

5 教學啟示與思考

5.1 注重知識的“生長點”與“延伸點”

選擇恰當的問題是學生有效參與課堂的關鍵.雖然學生熟悉線段垂直平分線，然而要在網格中用無刻度直尺作出線段垂直平分線還是存在較大難度.在設計這堂課時，教師由淺入深，引導學生緊扣垂直平分線的定義，分線段在網格的格線上和不在格線上兩種情況探討，最后減少網格數逐步增加難度，總結平移和旋轉兩大基本方法.讓學生在環環遞進的問題中體會圖形的聯系與變化，在動手實踐過程中積累活動經驗、展現思考過程、交流收獲體會、激發創造潛能.從低起點的問題先導、系統化地建構聯系，到螺旋式上升的變式拓展，多維度的深度融合，契合學生的最近發展區，實現知識的生成習得與延伸拓展.

5.2 注重知識的理解生成與應用內化

數學知識的教學，應注重學生對所學知識的理解，體會數學知識之間的關聯.對于尺規作圖，學生不僅要知道作圖的步驟，而且還要知道實施這些步驟的理由.為了幫助學生真正理解數學知識，教師從考慮教學內容的特點出發，組織學生開展作圖操作活動，引導學生思考分析，運用知識判斷不同情形的不同作法，總結概括方法，思考幾種方法之間的聯系，建立起學生的學習經驗與數學知識生成過程之間的聯系，讓學生真正理解知識，印象深刻.

5.3 注重教會學生學習方法和總結方法

授人以魚不如授人以漁.傳授學生知識，不如傳授學生學習方法；傳授學生學習方法，不如引導學生自己總結方法[2].本節課的目的并不局限于教學內容，教師以知識為載體，教會學生思考和分析問題的方法，培養學生解決問題的能力，養成總結的習慣.

6 結語

教師要善于將教師的“教”和學生的“學”結合起來，在環環設問和步步探究中發揮學生的主觀能動性，提升學生的思維能力和幾何素養，重視學生知識的架構和方法的生成，讓學生成為學習的主人.