探析初中數學中轉化與化歸思想的實踐應用
江蘇省無錫市大橋實驗學校 陳建忠
初中數學呈現出的主要特征是抽象.很多數學問題需要通過聯想、分析、類比等思維進行轉換,才能夠將原本并不熟悉的問題轉化為已經掌握的問題,進而完成問題求解.而數學問題轉化的過程被稱為轉化與化歸.從本質上來講,轉化與化歸思想充分揭示了聯系數學問題實際,完成知識點轉化的過程,除卻原本就非常簡單的數學知識,其他的數學問題都需要經過轉化方式來實現求解.可見,轉化與化歸思想是求解數學問題的基本思想.本文中將就初中數學中的轉化與化歸思想的實踐應用展開詳細探討.
1 復雜問題簡單化
初中數學知識教學中,教師通常會引導學生將原本比較復雜的問題以化歸方式逐漸轉化為簡單問題,而學生先解決自己熟悉的簡單問題,最終逐步達到解決復雜問題的目的.該種解決問題的方式被稱為簡單化,是獲取復雜問題解題思路的主要依據.
例1如圖1,樓梯的高度為2 m,∠BAC=30°,此時在樓梯表面鋪設地毯,求地毯的長度.
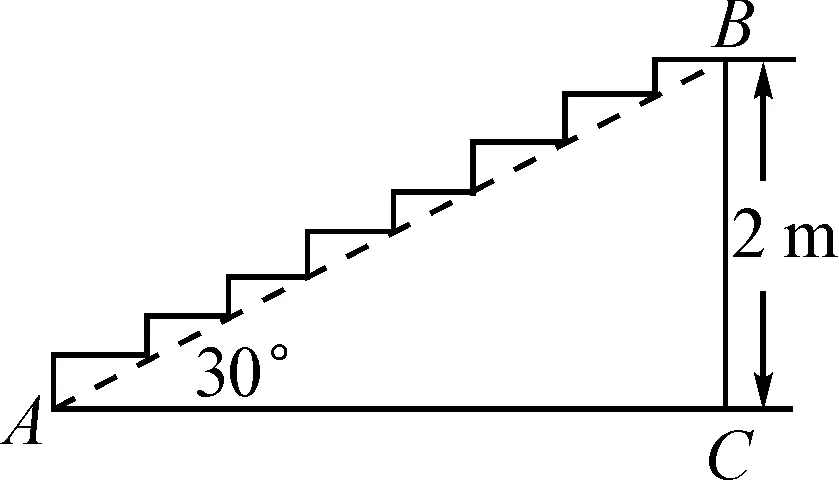
圖1
解析:連接AB.
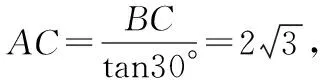
上述解題步驟中,率先考慮的思路是分別求出每個臺階上的地毯長度,然后將這些長度相加.但是,因為不知道每個臺階的具體高度和寬度,因此,如果直接采用這種長度相加的方式求解,思路會受到限制.如果在圖形中能夠觀察到將A,B兩點連接以后形成了多個小直角三角形,其中較小的銳角均為30°,而且題目中給出已知條件樓梯的高度為2 m,可以猜測將圖形中的小三角形轉化為大直角三角形.再思考轉化方法,發現將小直角三角形進行平移,能夠直接將各個臺階的寬度平移到AC上,與AC的長度相等,將小三角形的高度平移到BC邊上,長度與BC邊相等.因此,想要求解地毯鋪設的長度,只需要將BC邊和AC邊的長度求解出來,就能夠得到地毯的最小長度.經過重新轉化和猜想,將原本分散的條件集中起來,最終形成比較完整的解題條件,能夠快速解決問題.
2 高難問題概念化
有不少數學問題表面上看難度很大,但如果我們能透過表象,抓住本質,利用已知的概念等基礎知識進行化歸,難題也就迎刃而解.
例2已知一元二次方程ax2+bx+c=0(a,b,c為常數,a≠0)的根是x1=-3,x2=2,求關于x的一元二次方程a(x-5)2+7b(x-5)+49c=0的根.
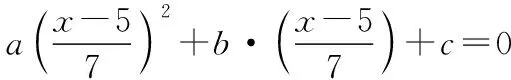
3 疑難問題常規化
有的問題屬于非常規問題,我們可以借助化歸與轉化的方式,讓問題變得常規化,從而利用常規的方式解決.
例3如圖2,將八個邊長為1的小正方形擺放在平面直角坐標系中,若過原點的直線l將圖形分成面積相等的兩部分,則直線l的函數關系式為________.
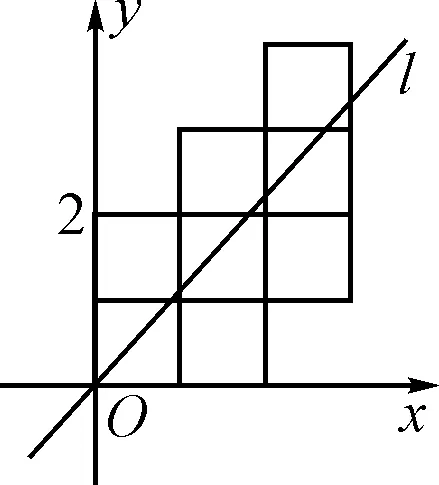
圖2
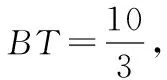
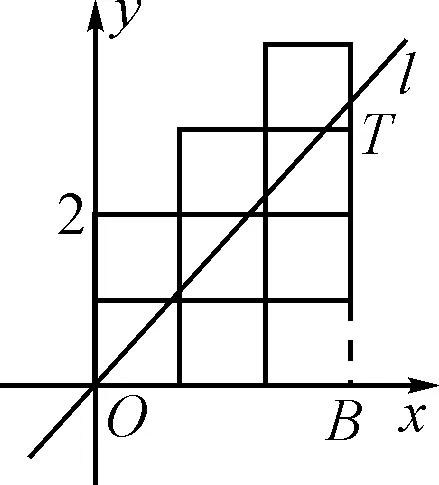
圖3
4 變數問題固定化
有些動態變化問題,讓學生捉摸不定.這時,我們盡可能利用化歸的方式,將問題轉換為固定的量.
例4如圖4,在ABCD中,∠B=60°,AB=6,BC=4,點E為邊AB上的一個動點,連接ED并延長至點F,使得DE=2DF,以EC,EF為鄰邊構造EFGC,連接EG,則EG的最小值為________.
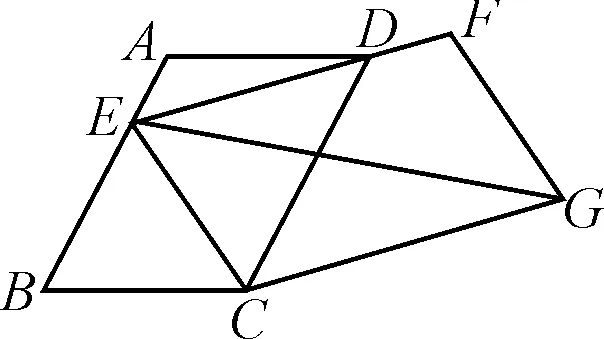
圖4
解析:本題中,EFGC隨時處于運動中,EG的長度更是沒法確定.設DC與EG交于點T,根據相似,我們可以很快將EG的長度變為問題轉化為ET的最小值,從而利用“點到直線的垂線段最短”“平行線間距離處處相等”,求得ET的最小值,從而求得EG的最小值.
5 未知問題已知化
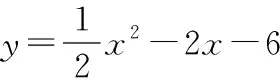
(1)求線段PE長的最大值;
(2)作PF∥AC交BC于F,求EF長的最大值.
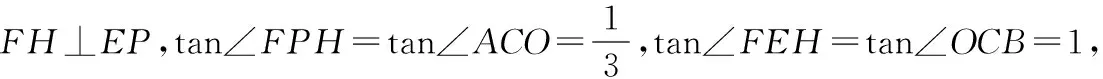
6 抽象問題直觀化
抽象問題是初中數學中比較常見的問題.很多時候,因為對知識點不熟悉而導致學生不能完全解決相應的數學問題.為提升學生的解題效率,幫助學生形成更加直觀的解題思維,可以將抽象問題進行轉化,促使其中的已知條件直觀化.借助圖形方式直觀觀察抽象問題,了解不同數值之間的關系.
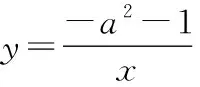
解法1:由k=-a2-1=-(a2+1)<0,得函數圖象分布在第二、四象限,而且每個象限內y的數值都會隨著x值的增大而增大.
由A(-4,y1),B(-1,y2)在第二象限,且-4<-1,得0 由C(2,y3)在第四象限,得y3<0. 因此,y3 解法2:將已知條件中的三個點均畫在圖象上,根據圖象可以觀察到y3 對很多學生來說,函數問題都是比較復雜的問題,因為之前較少接觸函數相關知識,學生一時之間無法掌握函數知識的規律.在面對函數問題時,學生總感覺力不從心.實際上,函數和方程之間可以實現轉化,借助轉化與化歸思維,將函數問題轉化為方程問題,依據自身已掌握的方程知識,完成問題求解.在此過程中,教師對學生進行教學引導,幫助學生形成轉化與化歸思維. 例7已知關于x的函數y=(m+6)x2+2(m-1)x+(m+1)的圖象和x軸總有交點,求解m的取值范圍. 解析:若m+6=0,則m=-6,函數y=-14x-5的圖象和x軸有相交.所以m=-6符合題意. 若m+6≠0,即m≠-6,則問題轉化為關于x的一元二次方程(m+6)x2+2(m-1)x+(m+1)=0總有解. 由Δ≥0,得 4(m-1)2-4(m+6)·(m+1)≥0. 總體來說,數學轉化思想能夠滲透到任何數學問題中,其將大部分學生都不了解且無法解答的數學問題以轉化思維進行簡單化處理,促使其他的數學知識替代原本的數學條件.而知識轉化過程中,學生的數學思維能力增強,數學核心素養也隨之提升.學生的數學能力會隨著數學知識的學習不斷增加,數學思維也會因為數學知識的理解而逐漸遷移.鑒于該種情況,教師在具體教學實踐中,需要注意教學方法的選擇,給予學生足夠的思考空間,讓學生將轉化與化歸思維貫穿于數學解題過程.如此一來,學生能夠在面對數學問題時大膽猜測,明確數學化歸目標,最終找到解決數學問題的有效途徑.7 函數問題方程化
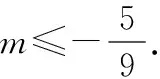
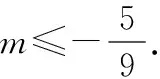
8 總結

