齊次線性方程組解的結(jié)構(gòu)問題的教學(xué)設(shè)計

裴慧敏 （江蘇師范大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院，江蘇 徐州 221116）

1 引 言

在中學(xué)數(shù)學(xué)中，對于給定的線性方程組，一般只需要求出它的解即可，這對于線性方程組的研究是遠遠不夠的.對于給定的線性方程組，它可能無解、有唯一解或者有無窮多解.當(dāng)線性方程組無解或者有唯一解的時候，都很容易表示出來.但是，當(dāng)線性方程組有無窮多解的時候，不可能將所有的解都一一表示出來.那么，如何將這無窮多解以一種比較簡潔的形式表示出來呢？

本文主要是關(guān)于齊次線性方程組解的結(jié)構(gòu)問題的教學(xué)設(shè)計.首先，通過問題引入，引出齊次線性方程組的解的結(jié)構(gòu)問題.再通過不斷引導(dǎo)學(xué)生，給出基礎(chǔ)解系、結(jié)構(gòu)式通解的相關(guān)概念.最后，給出求結(jié)構(gòu)式通解的方法.本文結(jié)尾，也結(jié)合本節(jié)課知識點，融合課堂思政，做到教書育人相結(jié)合.

2 教學(xué)過程

2.1 問題引入

首先，我們來回顧一下，對于給定的齊次線性方程組，如何求出它的解.

解齊次線性方程組

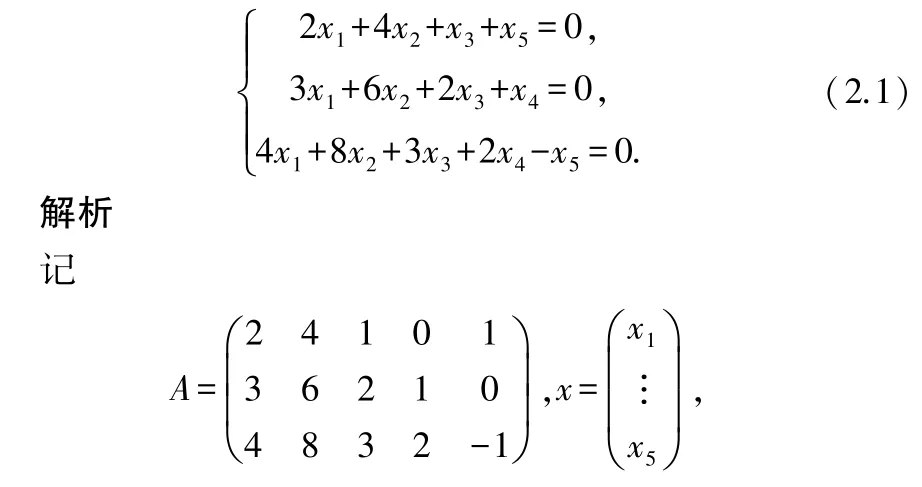
則齊次線性方程組（2.1）可以表示成矩陣形式

其中，就是要求的齊次線性方程組的解.

通過前面的學(xué)習(xí)我們知道，要求，首先就要對方程組的系數(shù)矩陣施行初等行變換將其化為行最簡形矩陣：

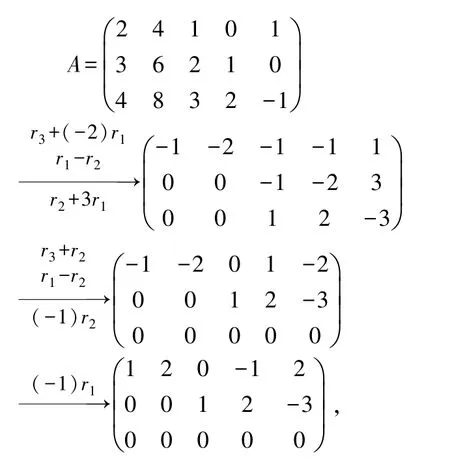
顯然，（）＝2＜5，所以，原齊次線性方程組有無窮多個解，其通解為

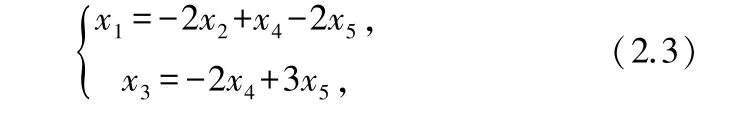
其中，，是自由未知量.

把自由未知量，，依次取為任意常數(shù)，，，則方程組＝0 的通解還可表示為

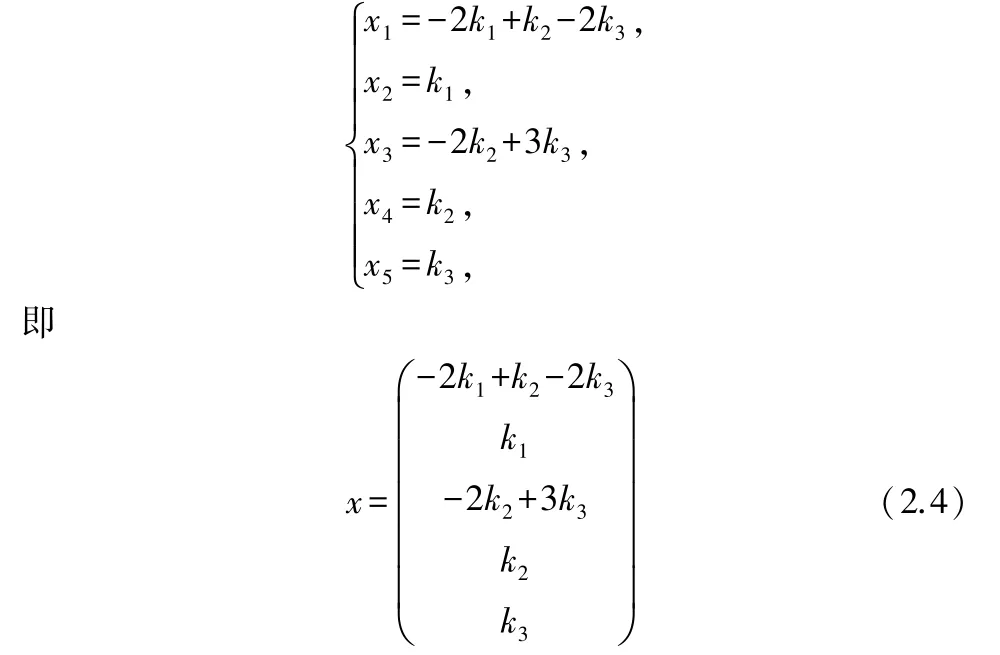
顯然，當(dāng)未知量的個數(shù)比較多且自由未知量的個數(shù)比較少時，如果繼續(xù)用（2.4）式來表示齊次線性方程組＝0 的解，就會比較煩瑣.

對于一般的齊次線性方程組＝0，當(dāng)它有無窮多解時，如何以一種比較簡潔的形式將這無窮多解表示出來呢？這一問題值得我們?nèi)パ芯浚@就是齊次線性方程組解的結(jié)構(gòu)問題.

2.2 研究問題

給定元齊次線性方程組

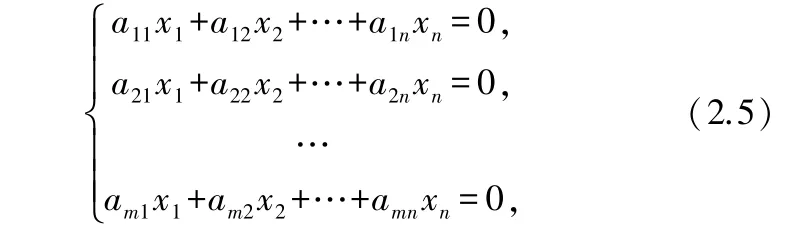
則齊次線性方程組（2.5）可以表示成矩陣形式

其中，是系數(shù)矩陣，是齊次線性方程組（2.6）的一個解向量或者解.

注意到，當(dāng)齊次線性方程組＝0 有無窮多解時，它的所有解向量就可以組成一個集合，記為解集那么，根據(jù)向量組的極大無關(guān)組的定義，如果我們能夠找到解集的極大無關(guān)組，那么，解集中的任何一個解向量都可以由該極大無關(guān)組線性表示，即齊次線性方程組＝0 的無窮多解可以由該極大無關(guān)組線性表示.

將解集的極大無關(guān)組記為，，…，α，顯然，它需要滿足如下三個條件：

（1），，…，α是解集的一個部分組；

（2），，…，α線性無關(guān)；

（3）解集中的任一向量都可由，，…，α線性表示.

對于這個極大無關(guān)組，我們將它稱為齊次線性方程組＝0 的基礎(chǔ)解系.下面，我們具體給出基礎(chǔ)解系的概念.

定義2.1齊次線性方程組＝0 的一組解，，…，α稱為它的一個基礎(chǔ)解系，如果

（1），，…，α線性無關(guān)；

（2）方程組＝0 的任一解都可由，，…，α線性表示.

顯然，如果，，…，α是方程組＝0 的一個基礎(chǔ)解系，那么方程組＝0 的任意一個解都可以表示成如下形式：

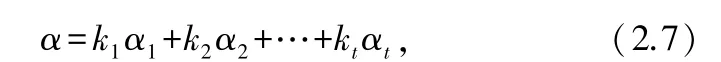
其中，，…，k是一組常數(shù).反之，對于任意一組數(shù)，，…，k，也都是方程組＝0 的一個解，因為

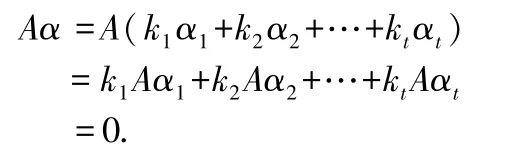
我們將式（2.7）稱為齊次線性方程組＝0 的結(jié)構(gòu)式通解.

對于一般的齊次線性方程組＝0，當(dāng)它有無窮多解時，我們就可以用結(jié)構(gòu)式通解將它的無窮多解簡潔地表示出來.那么，對于給定的齊次線性方程組＝0，如何求出它的結(jié)構(gòu)式通解呢？

要求齊次線性方程組＝0 的結(jié)構(gòu)式通解，首先就要求出它的基礎(chǔ)解系.根據(jù)基礎(chǔ)解系的定義，我們思考：

（1）什么樣的齊次線性方程組＝0 存在基礎(chǔ)解系？

（2）若存在，如何求出齊次線性方程組＝0 的基礎(chǔ)解系？

下面，我們將圍繞這兩個問題進行討論.

首先，我們來看第一個問題.

由前面的學(xué)習(xí)，我們知道只含零向量的向量組不存在極大無關(guān)組，也就是說，只有當(dāng)齊次線性方程組＝0 有非零解（無窮解）時，即（）＜時，它才存在基礎(chǔ)解系.

接下來，我們從秩的角度出發(fā)，對第二個問題進行研究.

設(shè)（）＝，的行最簡形矩陣為

當(dāng)＝0 時，為零矩陣，即＝0.此時，任一維列向量都是方程組＝0 的解.由于＝0 與＝0 同解，所以，任一維列向量都是方程組＝0 的解.也就是說，＝0 的解集是由所有的維列向量構(gòu)成的.通過前面的學(xué)習(xí)知道，維單位向量組，，…，ε是解集的一個極大無關(guān)組，所以，任意個線性無關(guān)的維列向量都是方程組＝0 的一個基礎(chǔ)解系.

當(dāng)0＜＜時，不妨設(shè)的前個列向量線性無關(guān)，由于的列向量組與的列向量組具有完全相同的線性關(guān)系，所以，矩陣可設(shè)為

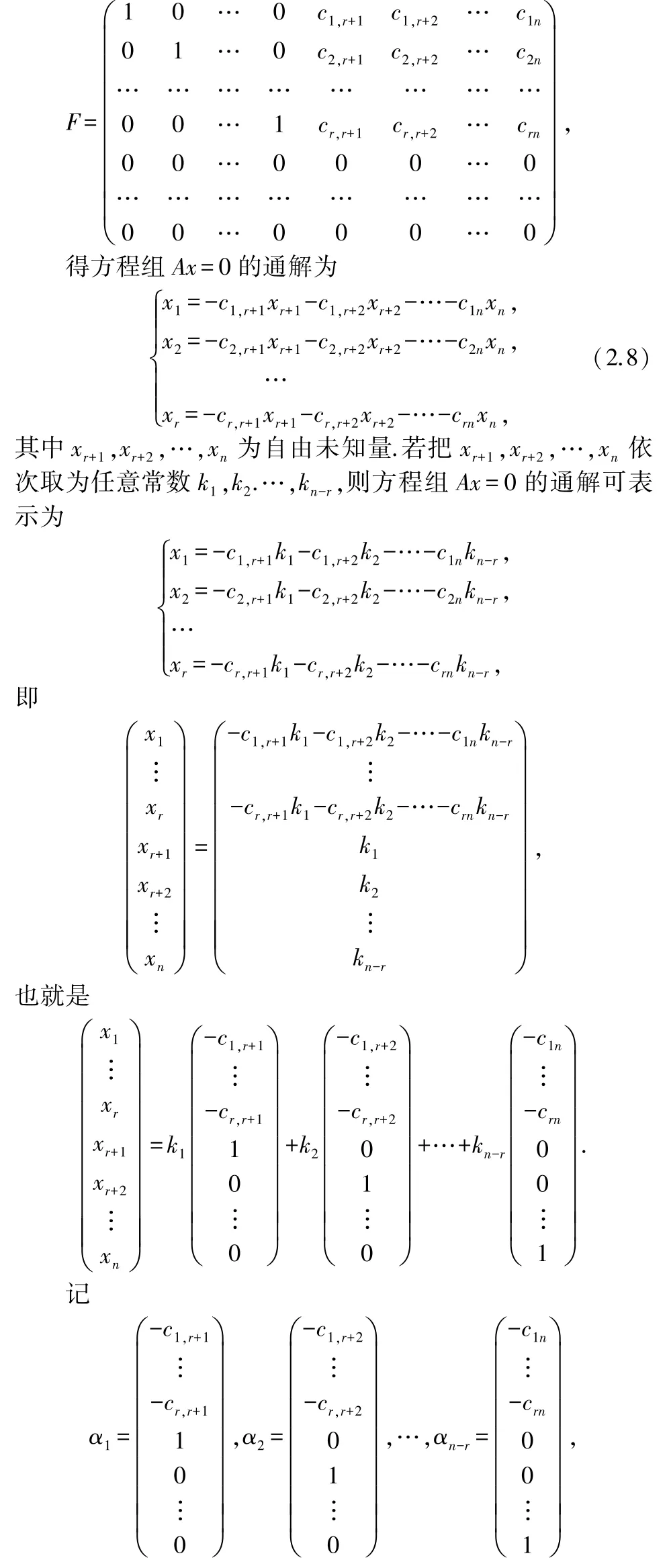
則方程組＝0 的通解可表示為

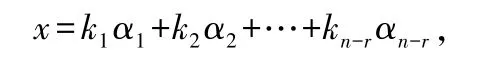
即＝0 的任一解都可由，，…，α線性表示.

如果，，…，α又是方程組＝0 的-個線性無關(guān)的解，那么，，，…，α就是方程組＝0 的基礎(chǔ)解系.接下來，我們只需證，，…，α是方程組＝0 的-個線性無關(guān)的解即可.

通過觀察我們發(fā)現(xiàn)：在方程組＝0 的通解（2.8）中把自由未知量x，x，…，x依次取-組值：

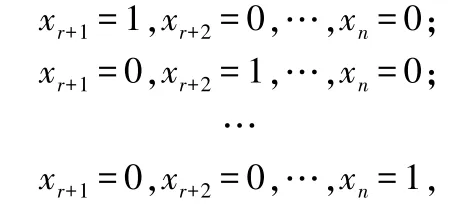
就得到了，，…，α，也就是說，，…，α是方程組＝0 的-個解.

接下來，我們只需證明，，…，α線性無關(guān)即可.為此，建立向量方程

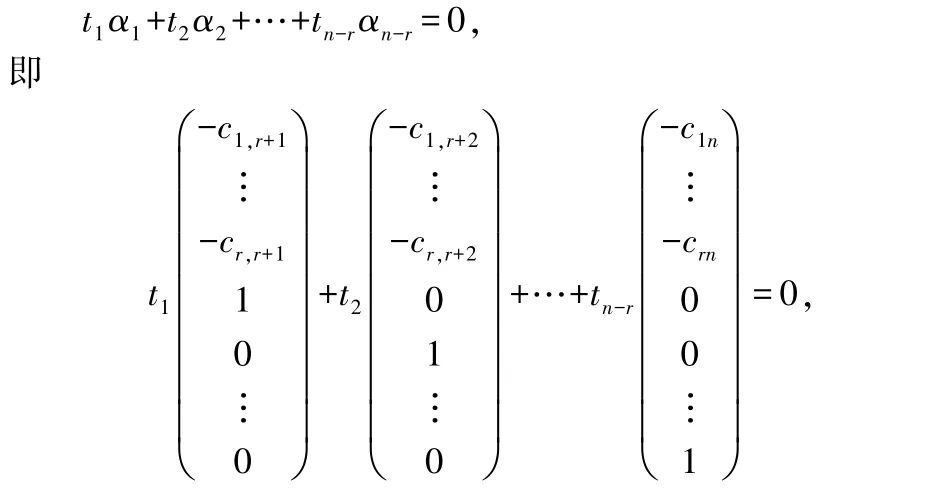
解得＝＝…＝t＝0，也就是，，…，α線性無關(guān).結(jié)合上述分析可得，，，…，α是方程組＝0 的基礎(chǔ)解系.

進而，可以得到下面的定理：

設(shè)是×矩陣，若齊次線性方程組＝0 有非零解，即（）＜，則它的基礎(chǔ)解系存在，且基礎(chǔ)解系所含的向量個數(shù)等于-（）.

上述分析還給出了求基礎(chǔ)解系的方法：

第1 步 用初等行變換把系數(shù)矩陣化成行最簡形矩陣.

第2 步 寫出方程組＝0 的通解，然后在通解中把自由未知量x，x，…，x依次取-組值：

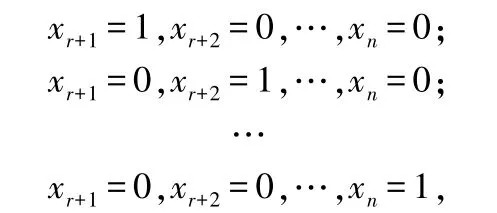
就可得到方程組＝0 的-個線性無關(guān)的解，，…，α，也就是＝0 的一個基礎(chǔ)解系.

第3 步 寫出齊次線性方程組＝0 的結(jié)構(gòu)式通解：

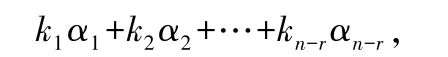
其中，，…，k為任意常數(shù).

下面，我們通過例題來看一下具體如何求出齊次線性方程組的結(jié)構(gòu)式通解.

求齊次線性方程組的結(jié)構(gòu)式通解.

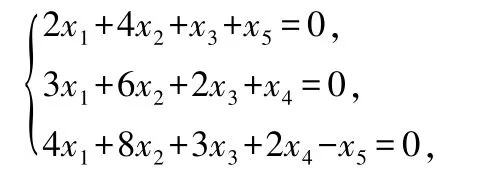
要想得到齊次線性方程組的結(jié)構(gòu)式通解，首先就要求出它的基礎(chǔ)解系.

由2.1 節(jié)可知，齊次線性方程組的通解為

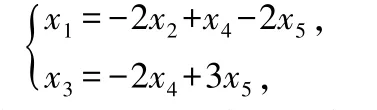
其中，，是自由未知量.

則，，是原方程組的一個基礎(chǔ)解系，所以原方程組的結(jié)構(gòu)式通解為

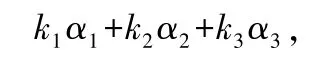
其中，，為任意常數(shù).

課后思考：齊次線性方程組＝0 可以看成是一種比較簡單的線性方程組.那么，對于一般的線性方程組＝，當(dāng)它有無窮多解時，如何求出它的結(jié)構(gòu)式通解呢？容易看出，當(dāng)一般的線性方程組＝有無窮多個解時，與其對應(yīng)的齊次線性方程組＝0 也有無窮多個解.那么，可否借用齊次線性方程組＝0 的基礎(chǔ)解系給出＝的結(jié)構(gòu)式通解呢？這個問題，我們將在下節(jié)課與大家一起探討.

2.3 內(nèi)容小結(jié)

本次課程通過具體的例子引入了基礎(chǔ)解系的概念.并在此基礎(chǔ)上，引導(dǎo)學(xué)生得到了結(jié)構(gòu)式通解的概念.然后，從秩的角度出發(fā)，得到了基礎(chǔ)解系的求解方法，進而得到了齊次線性方程組的結(jié)構(gòu)式通解.最后，結(jié)合具體的例題，給出了求解齊次線性方程組的結(jié)構(gòu)式通解的方法.本次課程從簡單問題入手，通過一步步引導(dǎo)學(xué)生，結(jié)合學(xué)生之前所學(xué)知識一步步達到教學(xué)目的.這種教學(xué)設(shè)計思路，不僅能夠吸引學(xué)生的注意力，提高他們的學(xué)習(xí)興趣，而且還能引發(fā)他們的思考，培養(yǎng)他們發(fā)現(xiàn)問題、分析問題和解決問題的能力.

3 課堂思政

本次課程我們主要學(xué)習(xí)了齊次線性方程組的基礎(chǔ)解系，借助基礎(chǔ)解系，我們研究了齊次線性方程組的結(jié)構(gòu)式通解.通過本節(jié)課的學(xué)習(xí)，我們能夠發(fā)現(xiàn)，結(jié)構(gòu)式通解能夠使齊次線性方程組的解的表示變得更加簡潔優(yōu)美.數(shù)學(xué)中有解的結(jié)構(gòu)，我們在人生的道路上能否取得成功也有解的結(jié)構(gòu)，偉大的科學(xué)家愛迪生說過：“成功等于1%的靈感加99%的汗水.”99%的汗水能夠使我們的人生變得更加完美.所以，不管是在求學(xué)過程中，還是在以后的工作中，想要成功就要付出努力.只要堅定信心，勇往直前，就終將會實現(xiàn)人生理想和目標(biāo).