基于有限元與能量方法結合的前圍板阻尼片布置優化

常光寶，張吉健，羅德洋，白長安

(1.上汽通用五菱汽車股份有限公司技術中心，廣西 柳州 545007；2.武漢融聲奇科技有限公司，武漢 430014；3.西安交通大學 機械工程學院，西安 710049)

0 引言

阻尼片在汽車行業使用廣泛，這些阻尼材料通常由一些柔性材料制作而成(如合成橡膠、橡膠、軟木、高密度泡沫和層壓材料)，被貼裝在板件上，用以減小車身板件的振動。正因為這樣，阻尼片能夠改善金屬薄板的隔聲效果。優化這些布放位置不僅能夠增強隔聲效果，還能契合成本控制、輕量化的發展需求。

數值計算已經成為除理論分析和實驗測試外的常用研究方式[1]，通過有限元的數值計算方法研究結構隔聲特性建立在經典力學基礎之上，主要包括有限元法和邊界元法等。王智文[2]、張若平[3]等對汽車地板阻尼材料與車內振動噪聲性能的聯系進行了研究，并對車身結構的模態應變能進行分析，優化阻尼，提高NVH性能。趙建軒[4]、鄭玲[5]等進一步結合壁板貢獻量，降低振動噪聲。梅勝軍等[6]將模態應變能、壁板貢獻量和模態貢獻量綜合考慮優化阻尼。張一麟等[7]通過觀察車身模態并結合壁板貢獻度的方法優化阻尼。除了上述的有限元建模外，統計能量方法也是常用的數值計算方法[8]，劉春蕾等[9]將60 km/h勻速行駛工況作為計算工況，對司機耳旁聲壓級進行預測，驗證了統計能量分析方法預測噪聲的有效性。統計性方法建立在統計力學基礎之上，其主要代表有統計能量法等。黃鼎友等[10]利用統計能量法對前圍板的隔聲性能進行了預測，并與實驗測試的結果進行了對比，兩者趨勢基本一致。但是統計能量法基于統計思想，很難考慮模型細節的影響，因此在計算精度方面有著天然的劣勢，主要用于趨勢的預測。

在統計能量分析中，模型分子系統或者分塊的概念成為近年來的分析熱點。相對于單純的基于網格的有限元方法，分塊方法可把若干網格組合成一塊，這樣整個系統分為若干塊，相對于原始網格來說，分塊的自由度會降低很多，分析效率會提升很多。基于能量處理的方法可以創建更緊湊的能量模型[11-14]，這種方法基于模態，并可以自動將結構劃分成多塊，分別對每一塊計算整體的分布矩陣。這種方法將原來的有限元模型縮減到對每一塊的計算上，可以快速地進行指定載荷下的能量評估。

本文采用有限元模型和能量后處理相結合的方法，通過建立更精簡的能量模型描述結構部件的動力學響應，并通過編程的方式實現自動計算每個單元塊對阻尼的敏感性響應結果。這種方法基于現有的結構模態和剛度質量矩陣，模型中的各結構部件自動劃分成很多單元片，并且每個單元片上進行“分布矩陣”組裝。該方法可以大幅降低模型計算量，有效提高數值計算效率；同時基于其高效性，可以把該方法集成到優化工作流程中。

1 理論介紹

有限元方法與能量分析方法結合的流程中，基于結構動力學的有限元方法不贅述。能量分析方法是基于有限元結構模態與模型的剛度-質量矩陣(K_M矩陣)來進行分塊處理和能量分析，該過程稱為能量后處理過程[15]。

能量后處理過程中，首先將有限元模型分解成一系列單元集合(Patch，下文稱“單元塊”)。每一個單元塊是一系列屬于相同有限元模型部件的連續的單元集合，且假設在每一個單元塊上能量級均勻分布。因此，單元塊是這種能量后處理方法的基本構成。圖1展示了自動劃分的某示意板件的單元塊，每個小單元塊里面有若干有限元單元網格。

圖1 單元塊自動劃分示意圖

(1)

式中：Ki、Mi和Kip、Mip分別為模態坐標系和物理坐標系下的第i個單元塊上的剛度陣和質量陣。分布式矩陣Ki和Mi只需計算1次，后續各種載荷作用下的響應計算均調用。

計算單元塊的分布式矩陣優勢在于可以在單元塊的子結構上快速地進行能量計算。也就是說，在各種載荷工況下都可以計算出第i個單元片的動能、勢能和耗散功率：

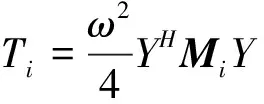
(2)

(3)

(4)

式中：Y為模態坐標位移，Ti、Vi、Wi分別為單元的動能、勢能和耗散功率，ηi為阻尼損耗因子，ω為圓頻率。

當只有遲滯阻尼決定阻尼片的能量耗散時，可以通過阻尼損耗因子ηi來定義第i個單元塊上的阻尼。在每個單元塊上定義不同的阻尼因子，就會形成不均勻的阻尼分布。經過循環計算后，可以計算得到哪些單元塊對阻尼片較為敏感。

板件的隔聲特性仿真分析通常需要用擴散聲場作為載荷來模擬無規入射的聲能量。擴散聲場可以通過多個采樣的不相關的、在空間中沿著任意方向傳播的平面波疊加獲得，可以用來模擬一個弱穩態隨機過程，描述這一理論模型的解析表達式如下：

(5)

(6)

式中：k為波數，c為聲速，d為聲場中2個觀察點之間的距離。

2 技術路線

采用數值分析軟件與自編程序相結合的方式進行前圍板阻尼片位置優化方法研究，研究對象為含鈑金件和復合層的前圍板結構，其中板件的有限元模型已經確定，采用基于有限元方法與能量方法的敏感性分析流程確定阻尼片的布置位置，技術路線如圖2所示。

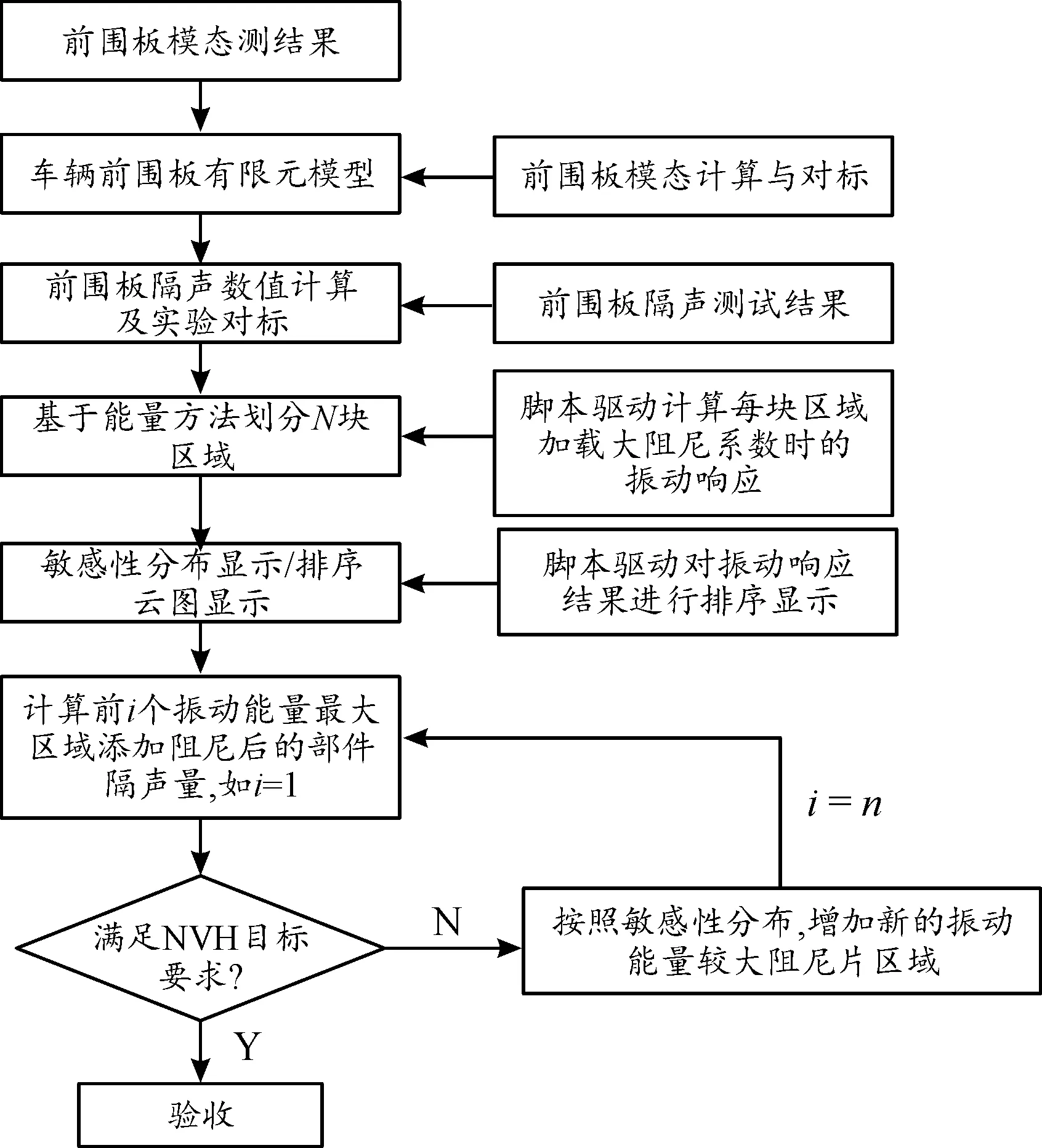
圖2 技術路線框圖

具體實施所用方法和內容如下所示：

1)在有限元分析軟件Nastran中，采用有限元分析的方法進行車輛前圍板的有限元模態分析；

2)在聲學分析軟件Actran中，采用能量分析方法建立能量分析模型，在輸入模態結果和剛度質量矩陣(KM矩陣)數據后，設定N個有限元網格組成一個單元塊子系統。分析模型中考慮擴散聲場激勵加載到結構模態上，擴散聲場采用25個抽樣樣本構成隨機的分布式載荷激勵；

3)使用Python語言編寫板件不同單元塊對阻尼的敏感性分析程序。因為結構阻尼被認為在各個單元塊上是相同的，優化流程最終會得到在各個單元塊上阻尼材料的分布量。通過監測擴散聲場載荷下的板的法向均方速度來判定板件不同區域對阻尼的敏感性；找到n個阻尼片的最優分布方案：

① 對于每一個單元塊，應用一個局部阻尼值；

② 計算對于每一種阻尼材料分布方案的整個板件法向速度的均方值；

③ 每一步都進行針對待優化板件的白車身有限元模型的能量后處理。使用分布矩陣計算每一種阻尼優化方案的殘余矩陣。

4)挑選出n個單元塊的法向振動速度均方值最小的位置添加阻尼。

在采用傳統直接頻響法進行每一步計算時，模型自由度由單元數量決定。而能量后處理法中，模型自由度由單元塊數量決定。文中優化流程的每一步計算在采用能量后處理方法時，計算模型的自由度都被降低到最少，計算效率更高。在最終驗證計算時，采用直接頻響法，以確保優化結果的準確性。

3 前圍板隔聲量性能研究及聲學優化案例

3.1 前圍板隔聲量性能分析

前圍板隔聲量計算流程如圖3所示。隔聲量分析模型中，定義前圍板結構各部分材料參數，并導入一側聲空間模型，定義為空氣材料屬性；模型中通過定義耦合面的方式把結構模型和空腔模型耦合起來，保證信息可以正常傳遞。模型中定義擴散聲場激勵加載到結構模型上，擴散聲場采用25個抽樣樣本構成隨機的分布式載荷激勵。

圖3 前圍板隔聲量計算流程框圖

隔聲量計算模型中，前圍板結構有限元模型與聲空間有限元模型組合成前圍板隔聲量計算聲振耦合分析模型，模型組成示意圖如圖4所示。

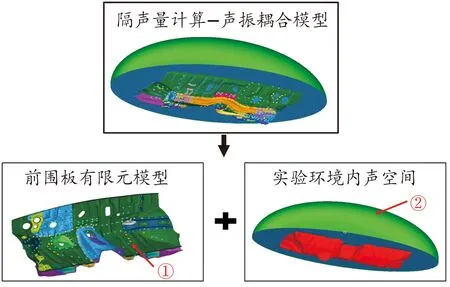
圖4 隔聲量計算-聲振耦合模型組成示意圖

圖4中，①為擴散聲場激勵，模擬無規律入射聲場激勵；②為APML邊界，模擬無反射的聲場邊界。前圍板鈑金件和阻尼材料參數如表1所示，阻尼材料的阻尼隨頻率變化。

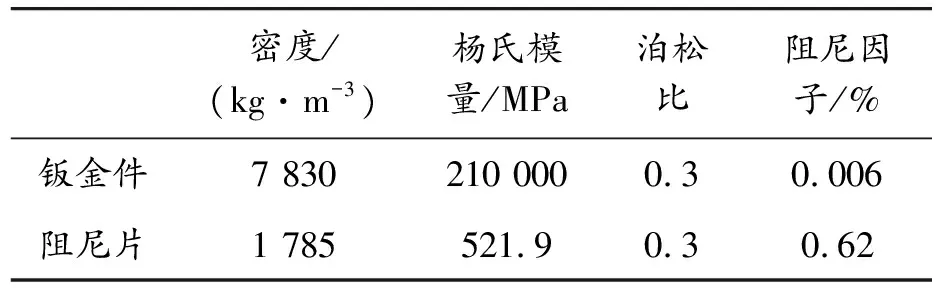
表1 材料參數

隔聲量計算完畢，得到隔聲量曲線，為了驗證仿真計算精度和方法的有效性，取相同模型的實際樣件做隔聲量測試。前圍板隔聲測試試驗在同濟大學聲學研究所進行，測試方法按照GB/T 19889.10—2006小建筑構件空氣聲隔聲的實驗室測試方法進行，隔聲室由兩間相鄰的混響室組成，如圖5所示。試驗過程中前圍板試驗件裝置在公共隔墻的開口上，測試溫度為16 ℃，相對濕度為80%。試驗采用B&K公司的PULSE 3560C作為聲源的信號發生器及數采系統，激勵信號為白噪聲信號。

圖5 前圍板隔聲量測試實驗示意圖

通過3次測試獲得的帶阻尼片前圍板模型的隔聲量數據如圖6中紅色實線所示；圖中藍色虛線為采用專業聲學軟件計算得到的帶阻尼片前圍板模型的隔聲量數值模擬數據。

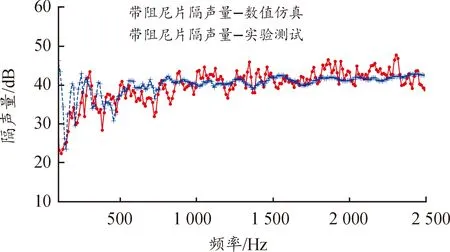
圖6 帶阻尼片前圍板隔聲仿真與測試結果曲線

從圖6中對比情況來看，兩者曲線走向趨勢一致，吻合度較高，其中在80 Hz以下頻段，隔聲計算值與試驗值差距較大，這是由于低頻一般受邊界條件影響較大，而在仿真模型中難以施加與試驗狀態完全一致的邊界條件；在80～2 500 Hz，隔聲計算值與試驗結果趨勢基本一致，計算模型滿足工程計算的要求。曲線均在100 Hz處(曲線起始頻率)隔聲量最小，符合經典板件隔聲量曲線中結構共振區隔聲量最低的趨勢，100～350 Hz為隔聲量增大區域。350～450 Hz隔聲量逐漸降低，達到吻合頻率區，該區間內入射聲波的波長在壁板上的投影與壁板中彎曲波的波長相近或相等時，發生吻合效應。450 Hz之后的隔聲量曲線呈現逐漸增大的趨勢，且實驗與數值仿真吻合度較高。計算模型實現了2 500 Hz以內頻段的隔聲效果，為阻尼片在地板高頻段的NVH性能表現提供了預測手段。

3.2 基于能量后處理的阻尼敏感性分析

前圍板隔聲量計算模型搭建完成且完成隔聲量對標后，在后續敏感性分析和位置優化中作為初始輸入的基準模型。在聲學分析軟件Actran中，采用能量分析方法建立能量分析模型，分析模型基于3.1章節隔聲量計算模型，在輸入模態結果和剛度質量矩陣(KM矩陣)數據后，設定N個有限元網格組成一個單元塊子系統。其中前圍板結構模態結果如圖7所示，圖中展示前6階結構模態的模態位移振型云圖。

圖7 前圍板結構有限元模態位移振型云圖(前六階模態振型)

其中，第一、二、五階顯示局部模態振型；第三、四、六階顯示前圍板板件整體模態振型。在做能量分析時，可以設定N個有限元網格為一個單元塊，若有限元網格數為S個，最終可以生成的單元塊數即S/N個。前圍板模型中，有限元網格數為20 945個，如每個單元塊包含800個有限元網格，則最終生成25個單元塊；為了測試該方法的可靠性，研究了每個單元塊中包含200個有限元網格、400個有限元網格、800個有限元網格，共3種計算模型。加載擴散聲場激勵后，完成能量分析模型。在Python運行程序里設定阻尼循環加載腳本，最終獲得每個單元塊上的平均振速結果，生成每個單元塊對阻尼的敏感性云圖，如圖8所示。

圖8的計算結果中，(a)(b)(c)中左側圖片為安裝不同分組方式形成的不同網格數的單元塊數的分布圖，其中，(a)中每塊單元塊的網格數最少，所以單元塊數最多，(b)次之，(c)中單元塊數最少。3個分組圖中，右側圖片為加載擴散聲場激勵后獲得的敏感性分析云圖，圖中顏色代表每塊單元塊上加載大阻尼系數時整個板件的法向均方振動速度，藍色表示加載到該區域單元塊后，整個板件的振動較小；同理，紅色區域表示該區域加阻尼系數后整個板件的振動較大。

圖8 有限元不同分塊形式云圖

最終在方案選型階段粘貼阻尼片時，應主要粘貼在藍色區域，同上考慮到阻尼片質量和工藝加工的要求，從藍色區域逐次過渡到淺藍色、綠色區域、褐色區域、淺紅區域，最后再選擇深紅區域。從圖8的3種分塊方案來看，結果穩定性較好，均在右上區域呈現藍色且圍繞中間孔洞圓周分布，趨勢線較為一致。考慮到分塊越少，計算效率越高，后續分析時，采用圖8(c)方案即可。

3.3 基于敏感性分析的局部阻尼片優化

乘員艙內含大量隔吸聲材料，且吸聲材料在中高頻段的降噪效果更為明顯，改進空間較大；相對而言，在中低頻范圍內的隔聲性能，特別是如何提升100～500 Hz的隔聲量特性尤為關鍵。本案例中前圍板上原始阻尼片厚度均為0.002 m，總質量為0.85 kg，設定阻尼片增質不超過15%，優化阻尼片位置及其厚度。位置優化依托敏感性分析結果，從藍色區域開始，選取的區域內按原始厚度0.002 m，其總質量滿足原始阻尼片約90%的質量0.78 kg，并把此作為后續阻尼厚度優化的初始模型。

在阻尼厚度優化時，調用聲學軟件中自帶的NLOPT優化算法，以阻尼片厚度為優化變量，以隔聲量的平均值為優化目標，迭代20次，計算得到隔聲量最大的阻尼厚度方案。圖9為迭代后模型與原始模型的隔聲量曲線。

圖9 阻尼片厚度優化前后隔聲量曲線

圖9中，藍色虛線為初始模型隔聲量曲線，紅色實線為迭代優化后模型的隔聲量曲線；2條曲線整體走勢一致，優化后模型在140～190 Hz隔聲量優于原始模型隔聲量。在幾個特征峰值頻率處，如190、230、250、340和350 Hz等頻率處，優化后模型隔聲量優于原始模型隔聲量，驗證了該方法對于優化阻尼片敷設方案的可行性，同時說明了合理的阻尼片敷設方案對于提升隔聲量的重要性。

4 結論

1)基于現有結構模態和剛度質量矩陣的能量分析模型，在每個單元塊上進行“分布矩陣”組裝，并針對具體工況載荷進行計算，將板件結構進行分塊處理，并通過腳本實現在每一塊板件施加阻尼的計算方式，找到板件對阻尼最敏感的位置。在敏感區域通過自動厚度優化計算，找到各區域最合適的厚度，能夠有效地降低阻尼材料的使用量，減重降本。

2)借助聲學軟件基于Python語言的腳本開發，調用能量后處理方法，對阻尼片有限元建模和實現優化功能。僅需要已有的有限元結構模型作為輸入，不需要額外的計算，可非常方便地融入工業設計流程。

3)對于車輛整車阻尼片優化布置，可基于整車結構模態和結構剛度質量矩陣形成能量分析模型，快速獲得阻尼敏感性分析結果，且由于考慮真實工況激勵如路噪軸頭力等，可以快速獲得基于真實激勵的整車阻尼優化布置方案。對汽車鈑金件類零件的前期設計有較好的指導意義。