碳交易規制下供應鏈上下游企業綠色創新博弈研究

王依婷，李 芳

(上海理工大學 管理學院，上海 200093)

0 引言

《京都議定書》是全球第一部限制各個國家碳排放的國際法案，中國于1998年5月簽署并于2002年8月核準了該議定書。2015年9月3日，全國人大常委會批準中國加入《巴黎氣候變化協定》，成為完成了批準協定的締約方之一。中國在過去的快速發展中，遺留下了碳排放量過高的問題，2018年中國碳排放總量達100億t，約占世界總量的30%。2020年9月，習近平總書記在第75屆聯合國大會上首次明確了實現碳中和任務的時間點，即2030年碳達峰，2060年實現碳中和。在嚴峻的環境形勢下，減少碳排放，加快推進全國碳交易市場建設工作迫在眉睫。2021年7月11日，全國碳排放權交易市場在上海正式啟動，助力國家推進綠色低碳發展。

國內學者將綠色創新分為技術創新、制度創新與文化創新三方面，本文將與碳減排有關的綠色創新聚焦于技術創新。中國低碳網[1]提到：河北奧意新材料有限公司通過技術創新，生產的鋁塑共擠型材經實測夏季節約電能30%，冬季可提升室溫5 ℃左右，大大降低了生產過程中的碳排放，成功入選綠色技術創新典型案例。可見，綠色技術創新能夠提高企業的生產技術，也能減少溫室氣體的排放，是兼顧經濟效益和社會效益的有力手段。宋德勇等[2]認為，碳排放權交易通過提高企業的生產污染成本倒逼企業進行低碳技術的投入；周鍵等[3]發現企業的綠色技術創新對碳減排行為有3種影響：提高資源的利用效率、控制企業的環境風險和加快碳減排知識的傳播。因此，碳交易能夠促進企業的綠色技術創新，進而控制碳排放，實現生產方式的綠色轉型。上游企業的低碳創新可以帶動下游乃至整條供應鏈減少碳排放，上下游企業之間的綠色創新合作對于碳減排有著重要的意義。企業之間如何通過碳交易市場參與碳減排，怎樣提高上下游企業的碳減排合作意愿是具有現實意義的議題。

國內外學者對于供應鏈節點企業之間的綠色創新有大量的研究：Yu等[4]研究在消費者的綠色偏好和補貼條件下，制造商對產品綠色程度和生產數量的決策問題；Jamali等[5]發現雙渠道供應鏈中集中方案能實現產品更高程度的綠色度；Sinayi等[6]探討政府在整個供應鏈中扮演領導者的模型下，消費者剩余和環境因素對利潤和產品綠色度的影響；曲優等[7]將風險規避引入綠色創新水平影響；解學梅等[8]對長三角四百多家企業進行調研，實證分析綠色創新和供應鏈協調的關系；魏琦等[9]考慮在不確定需求下企業的決策受碳減排措施的影響；姜明君等[10]在研究綠色創新投入問題時，融入公平偏好理論；梁喜等[11]將消費者剩余作為社會責任納入搭建的供應鏈模型中，研究社會責任承擔比例對產品綠色度的影響。

結合碳限額交易的供應鏈問題研究包括：Xu等[12]研究了碳限額交易規制下由制造商和零售商組成的訂單型供應鏈的生產與減排決策問題；He等[13]基于經濟訂單量模型，分別研究了碳限額交易規則和碳稅規則下企業的生產批量問題；向為民等[14]運用計量經濟學的辦法對碳交易價格影響因素進行了分析；廖諾等[15]構建碳交易政策下電煤供應鏈全過程碳排放的系統動力學仿真模型；黃瑞芬等[16]探究碳交易規制背景下資金約束的供應鏈優化問題；林歡等[17]發現制造商和供應商都愿意通過碳減排實現社會責任；張令榮等[18]構建了2種碳交易路徑下減排策略選擇的博弈模型，結果表明外部路徑下上游企業的減排效率更高，且內外部交易路徑共存情形下碳減排效果比單路徑情形更好。

目前，對于碳配額交易體系下供應鏈協調問題研究較多，少有學者研究綠色創新博弈問題。在博弈方法的選擇上多為主從博弈，考慮主體有限理性的演化博弈較少被使用。鑒于此，構建了碳配額交易下上下游企業之間綠色創新合作的演化博弈模型，為提高上下游企業的碳減排合作意愿，助力碳交易市場的發展提供理論支持。

1 博弈模型的構建

1.1 模型描述與假設

搭建由供應商和制造商組成的二級供應鏈模型，在全球碳減排和我國碳交易市場正式啟動的背景下，考慮上游供應商為實現減排目的對產品進行綠色技術創新，以降低生產過程中的單位產品碳排放量。同時，由于溢出效應，下游制造商會獲得碳排放方面的好處；為了減少下游制造商這種“搭便車”行為對上游供應商綠色創新積極性的影響，要求下游制造商對上游供應商的研發創新給予一定補貼。由于綠色創新供應鏈上下兩級的碳排放率降低，在政府發放的配額固定的情形下，碳配額產生盈余，這部分盈余可以在碳交易市場上進行交易，獲得額外收益。相關假設如下：

1)假設供應商和制造商都屬于碳排放規制下的企業，都可以在碳交易市場上進行交易；

2)假設供應商批發給制造商的產品都能在市場上出售，即制造商每制造1單位產品消耗1單位批發產品，批發量和銷售量保持一致為q；

3)為便于模型分析，假定供應商和制造商在進行綠色創新前的原始碳排放量等于政府給定的配額，即es=Es，em=Em；

4)假設供應商進行綠色創新后會獲得一定程度的碳減排效果，將該減排比例設定為rs，溢出效應作用下下游制造商獲得減排比例為rm(0≤rm≤rs<1)；

5)考慮到消費者的綠色偏好，假定供應商進行綠色創新后會增加市場需求β，由于供應商和制造商同屬一條供應鏈，二者會獲得市場需求增量βq；

6)假設碳交易價格為pe，綠色創新后供應商在碳交易市場上將獲得額外收益(1+β)rsqpe，同理，制造商將會獲得額外收益(1+β)rmqpe；

7)假設上下游企業之間約定，若上游供應商綠色創新，而下游制造商“搭便車”不給予補貼，則會受到懲罰Nm；同理，下游制造商給予了補貼，而上游供應商拒絕創新，則會受到懲罰Ns。

符號與含義見表1，收益矩陣相關元素見表2。

表1 符號及含義

表2 收益矩陣相關元素

U1=y[(1+β)(ps-cs)q+(1+β)rsqpe-I+

(1+β)qd]+(1-y)[(1+β)(ps-cs)q+

(1+β)rsqpe-I+Nm]

(1)

U2=y[(ps-cs)q+qd-Ns]+

(1-y)(ps-cs)q

(2)

(3)

V1=x[(1+β)(pm-cm)q+(1+β)rmqpe-

(1+β)qd]+(1-x)[(pm-cm)q-

qd+Ns]

(4)

V2=x[(1+β)(pm-cm)q+(1+β)rmqpe-

Nm]+(1-x)(pm-cm)q

(5)

(6)

供應商和制造商的復制動態方程分別是：

(1+β)rsqpe-I+Nm+

y(βqd+Ns-Nm)]

(7)

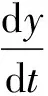
qd+Ns]

(8)

(9)

(10)

1.2 演化穩定點分析

為了正確處理均衡概念與動態演化過程均衡結果之間的關系，根據Friedman[19]提出的方法，供應商和制造商綠色創新博弈的演化穩定性可通過對演化系統的雅克比矩陣的局部穩定性分析得出。本模型的雅克比矩陣為:

(11)

其中：

a11=(1-2x)[β(ps-cs)q+(1+β)rsqpe-

I+Nm+y(βqd+Ns-Nm)]

a12=x(1-x)(βqd+Ns-Nm)

a21=y(1-y)(Nm-Ns-βqd)

a22=(1-2y)[x(Nm-Ns-βqd)-

qd+Ns]

(12)

則矩陣J的行列式和跡分別為:

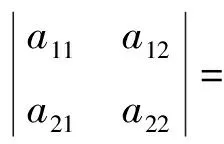
(1-2x)[β(ps-cs)q+

(1+β)rsqpe-I+

Nm+y(βqd+Ns-Nm)]

(1-2y)[x(Nm-Ns-βqd)-

qd+Ns]-xy(1-x)(1-y)·

(βqd+Ns-Nm)·

(Nm-Ns-βqd)

(13)

tr(J)=a11+a22=(1-2x)[β(ps-cs)q+

(1+β)rsqpe-I+Nm+

y(βqd+Ns-Nm)]+

(1-2y)[x(Nm-Ns-βqd)-

qd+Ns]

(14)

若上述均衡點滿足det(J)>0且tr(J)<0，則表明該均衡點是演化穩定點(ESS)。為計算簡便，令β(ps-cs)q+(1+β)rsqpe=A，各均衡點穩定性分析如表3所示。

表3 均衡點穩定性分析

根據上述的局部穩定性分析，可以得到結論:系統中存在4個穩定點(0，0)、(0，1)、(1，0)和(1，1)；均衡點(x*，y*)不滿足det(J)>0且tr(J)<0的條件，說明該均衡點不是ESS，對于擾動不具有魯棒性。

情形1當滿足條件I>A+Nm且Ns

情形2當滿足條件I>A+βqd+Ns且Ns>qd時，供應商進行綠色創新的收益并不吸引供應商，對于制造商而言供應商的違約支出大于其給予的補貼，制造商能夠從中獲益，此時局部均衡點為(1，0)，表明供應商選擇不進行綠色創新，制造商選擇給予供應商補貼。

情形3當滿足條件I

情形4當滿足I(1+β)qd時，供應商綠色創新的收益超過了綠色創新的成本，對于制造商而言，違約成本大于守約成本，此時的局部穩定點為(1，1)，表明供應商和制造商都選擇守約，進行綠色創新和補貼。

2 數值仿真與分析

使用Matlab 2020對模型進行演化仿真分析。在上述約束條件的基礎上，根據上海碳市場報告2020[20]和文獻[18]，將仿真分析的相關數值設定如下：pe=40，β=0.1，ps=1 000，pm=1 200，cs=900，cm=1 100，q=50，rs=0.5，rm=0.4，I=2 600。

博弈雙方的初始概率不是本文的研究重點，假設其為0.5和0.5，當制造商給予供應商的補貼選擇低策略時(d=1)，分別假設給予供應商和制造商的懲罰為低水平(Ns=200，Nm=500)，中水平(Ns=1 000，Nm=1 500)，高水平(Ns=1 500，Nm=2 000)3種情況下的演化路徑，如圖1所示。當d=1，Ns=200，Nm=500時，系統演化路徑趨于(0，1)；當d=1，Ns=1 000，Nm=1 500和Ns=1 500，Nm=2 000時，系統演化路徑趨于(1，1)，表明在低策略補貼情形下，懲罰力度的高低對于供應商的決策會產生影響，如果雙方商定的懲罰力度很輕，此時供應商會傾向于選擇不創新；當懲罰力度加強，供應商愿意進行研發創新；對制造商而言，愿意給予微薄的補貼去換取豐厚的收益。

圖1 低補貼政策下不同懲罰策略的影響曲線

當制造商對供應商的補貼選擇高策略時(d=30)，同樣假定懲罰力度的3種情形：低水平(Ns=200，Nm=500)，中水平(Ns=1 000，Nm=1 500)，高水平(Ns=1500，Nm=2 000)，演化路徑如圖2所示。當Ns=1 500，Nm=2 000時，系統演化趨于(1，1)；在Ns=200，Nm=500和Ns=1 000，Nm=1 500時，系統向(1，0)演化。結果表明，當補貼較高時，供應商愿意選擇進行綠色創新；對于制造商而言，如果懲罰不夠重，制造商傾向于違約，只有當懲罰力度較重時，違約成本對其而言是一筆不小的負擔，此時會約束制造商的違約行為。

圖2 高補貼策略下不同懲罰策略的影響曲線

圖3展示的是低懲罰力度下(Ns=500，Nm=1 000)不同補貼策略(d=10，d=20，d=30)，博弈雙方的演化路徑。當d=10時，博弈路徑向(1，1)演化；當d=20和d=30時，系統趨向于(1，0)。結果表明，低懲罰策略搭配低補貼策略能夠促進制造商和供應商兩方的合作，如果補貼價格過高，制造商會退出合作，寧愿選擇違約。

圖3 低懲罰策略下不同補貼力度的影響曲線

高懲罰力度下(Ns=1 500，Nm=2 000)不同補貼策略的演化路徑如圖4所示。不論d=10，d=20還是d=30，系統都向(1，1)演化。這說明，當懲罰力度足夠大時，不管補貼策略是低水平、中水平還是高水平，制造商和供應商都會選擇合作。

圖4 高懲罰策略下不同補貼策略的影響曲線

除了研究懲罰力度和補貼策略對制造商和供應商的策略選擇，還比較了不同碳交易價格對于制造商和供應商選擇的影響，將懲罰力度和補貼策略設定為中等水平(d=20，Ns=1 000，Nm=1 500)，研究pe=20，pe=40，pe=60時系統的表現。如圖5所示，當pe=20時，演化路徑趨于(0，0)；當pe=40時，路徑演變為(1，1)；當pe=60時，演化的速度越來越快。這表明碳交易價格對于供應商和制造商之間的合作博弈產生了至關重要的影響，交易價格過低，不吸引制造商和供應商進行綠色創新和補貼；當pe介于20～40范圍，制造商和供應商的策略選擇發生了質的變化，路徑演變從(0，0)轉變為(1，1)，說明存在1個值ε∈(20，40)，只有當碳交易價格超過這個值時，制造商和供應商才會考慮提高碳排放效率獲得盈余去碳市場上交易。

圖5 不同碳積分價格的影響曲線

3 結論

1)采取補貼或懲罰策略都會對博弈雙方的決策產生影響，當補貼不足時供應商傾向于拒絕進行技術創新；當懲罰力度不夠時，制造商傾向于拒絕合作。因此，博弈雙方補貼和懲罰的策略選擇會影響到碳減排創新合作意愿。

2)供應商對于補貼力度更加敏感，而制造商則對懲罰力度敏感。

3)碳交易價格對供應商和制造商之間的合作博弈有至關重要的影響，碳交易價格存在閾值，當價格超過閾值時供應商和制造商才會考慮是否要減少碳排放以獲得碳配額盈余去碳市場上進行交易。

本文尚存在一些不足之處。比如真實的市場環境中，供應鏈不是只有2個節點企業，會有3個乃至多個，未來研究可以進一步探討三方和多方的博弈；設置的碳排放配額是固定值，而根據歐盟的經驗，后續我國可能還會實行配額總量遞減政策，這一政策對博弈雙方之間的影響需要更深入的研究。