領(lǐng)航-跟隨型多移動(dòng)小車滑模編隊(duì)控制

李詠華,張 立,劉嘉睿,黃 崢,胡梓凱,廖世旺

(1.廣州大學(xué) 機(jī)械與電氣工程學(xué)院，廣州 510006;2.廣州市城市建設(shè)職業(yè)學(xué)校，廣州 510006)

0 引言

隨著智能制造業(yè)的快速發(fā)展，多機(jī)器人的應(yīng)用需求逐漸提升。相比于單個(gè)移動(dòng)小車，多移動(dòng)小車系統(tǒng)具有很多顯著的優(yōu)點(diǎn)[1]，較大的冗余性提高了容錯(cuò)性和魯棒性，可變的編隊(duì)控制保證了靈活性。目前，多移動(dòng)小車系統(tǒng)在倉(cāng)儲(chǔ)物流[2]、工業(yè)制造[3]和應(yīng)急救災(zāi)[4]等領(lǐng)域得到了廣泛的應(yīng)用。

在進(jìn)行多智能體編隊(duì)控制時(shí)所應(yīng)用的方法主要包括領(lǐng)航跟隨法[5-9]、行為法[10]、人工勢(shì)場(chǎng)法[11-12]和虛擬結(jié)構(gòu)法[13]4種。基于行為的多智能體編隊(duì)控制方法具有良好的魯棒性和靈活性，但是難以用數(shù)學(xué)分析描述系統(tǒng)而無法實(shí)現(xiàn)精確的編隊(duì)。基于人工勢(shì)場(chǎng)的多智能體編隊(duì)控制方法原理簡(jiǎn)單，適用于可自由運(yùn)動(dòng)的智能體編隊(duì)控制中，但對(duì)于非完整約束的情況難度較大。基于虛擬結(jié)構(gòu)的多智能體編隊(duì)控制方法需要編隊(duì)隊(duì)形保持同一個(gè)剛性結(jié)構(gòu)，因此靈活性和適應(yīng)性較差。基于領(lǐng)航跟隨的多智能體編隊(duì)控制方法原理簡(jiǎn)單，只需得到領(lǐng)航者期望軌跡和跟隨者相對(duì)位置即可，應(yīng)用最廣泛。

在領(lǐng)航-跟隨型的編隊(duì)控制研究中，張方方等[14]使用基于位置信息的速度補(bǔ)償算法對(duì)經(jīng)典的領(lǐng)航-跟隨法進(jìn)行改進(jìn)，并與人工勢(shì)場(chǎng)法相結(jié)合實(shí)現(xiàn)三輪差分實(shí)體機(jī)器人的編隊(duì)避障問題。王樂樂等[15]通過建立搜索樹擴(kuò)展方向與隊(duì)形之間的聯(lián)系，調(diào)整編隊(duì)方向以實(shí)現(xiàn)多智能體編隊(duì)路徑規(guī)劃。伍錫如等[16]通過設(shè)計(jì)狀態(tài)觀測(cè)器，實(shí)現(xiàn)了多智能體系統(tǒng)的環(huán)形編隊(duì)控制和目標(biāo)包圍。易國(guó)等[17]考慮了領(lǐng)航小車和跟隨小車之間的信息相互是局部的情況，為每個(gè)跟隨小車設(shè)計(jì)分布式估計(jì)算法估計(jì)領(lǐng)航小車的狀態(tài)，再根據(jù)跟蹤誤差實(shí)現(xiàn)編隊(duì)控制，但并未考慮時(shí)延等影響，同時(shí)會(huì)存在網(wǎng)絡(luò)負(fù)載波動(dòng)等影響。吳垠等[18]設(shè)計(jì)了不依賴移動(dòng)小車模型的模糊控制方法，實(shí)現(xiàn)了多移動(dòng)小車的編隊(duì)控制，但控制律過度依賴領(lǐng)航者模型，外部干擾對(duì)系統(tǒng)穩(wěn)定性的影響較大。

現(xiàn)有的編隊(duì)控制研究絕大部分針對(duì)編隊(duì)隊(duì)形不變的情況，但在現(xiàn)實(shí)情況中跟隨小車與領(lǐng)航小車的相對(duì)位置需要根據(jù)具體的任務(wù)而改變。針對(duì)多移動(dòng)小車的編隊(duì)控制和隊(duì)形變換控制問題，采用領(lǐng)航-跟隨法。首先，通過坐標(biāo)變換建立了輪式移動(dòng)小車的運(yùn)動(dòng)學(xué)模型、編隊(duì)控制的運(yùn)動(dòng)學(xué)模型，每個(gè)跟隨小車的期望位姿由領(lǐng)航小車當(dāng)前實(shí)際位姿和相對(duì)位置決定，基于移動(dòng)小車的跟蹤誤差設(shè)計(jì)了一種趨近律滑模編隊(duì)控制器，最后通過Matlab/Simulink數(shù)值仿真驗(yàn)證該控制器在多移動(dòng)小車編隊(duì)控制中的有效性。

1 預(yù)備知識(shí)

在圖論中，n個(gè)智能小車之間的通信拓?fù)浣Y(jié)構(gòu)可以用有向圖G=(V,E)表示，圖中節(jié)點(diǎn)0代表領(lǐng)航者。在拓?fù)浣Y(jié)構(gòu)中，將每個(gè)移動(dòng)小車抽象成節(jié)點(diǎn)，則所有節(jié)點(diǎn)的集合記為V={v1,v2,…,vn}。圖1中的箭頭表示智能小車間的通訊方式，其中圓點(diǎn)表示發(fā)送端，箭頭表示接收端，用e=(i,j)表示有向邊，表示智能小車i可以將信息傳遞給智能小車j，反之則不行。用E?N×N表示拓?fù)浣Y(jié)構(gòu)中所有邊的集合。

圖1 節(jié)點(diǎn)間通訊方式示意圖

圖G的鄰接矩陣為A=[aij]N×N，其中

在本文中，定義每個(gè)移動(dòng)小車只能訪問自身的狀態(tài)信息和領(lǐng)航小車的狀態(tài)信息，使用有向圖G=(V,E)描述領(lǐng)航小車和n-1個(gè)跟隨小車之間的通訊拓?fù)浣Y(jié)構(gòu)。通訊拓?fù)浣Y(jié)構(gòu)如圖2所示，其中{1}表示領(lǐng)航小車，{2,3,…,n}表示跟隨小車。鄰接矩陣A=[aij]N×N表示領(lǐng)航小車和跟隨小車間通訊關(guān)系的權(quán)重系數(shù)。

圖2 移動(dòng)小車間通訊拓?fù)浣Y(jié)構(gòu)示意圖

2 領(lǐng)航-跟隨型編隊(duì)控制的運(yùn)動(dòng)學(xué)模型

2.1 輪式移動(dòng)小車運(yùn)動(dòng)學(xué)模型

在由n個(gè)輪式移動(dòng)小車組成的領(lǐng)航-跟隨型編隊(duì)系統(tǒng)中，用i={1,2,…,n}表示第i個(gè)移動(dòng)小車，其中第一個(gè)為領(lǐng)航小車。假設(shè)移動(dòng)小車的速度較低，可以忽略車輪的橫向滑動(dòng)和行駛過程中所受的橫向力。建立以地面為參考的全局坐標(biāo)系XOY和以移動(dòng)小車為參考的小車坐標(biāo)系xoy，其中θi為小車移動(dòng)方向和水平方向的夾角。移動(dòng)小車的運(yùn)動(dòng)學(xué)模型如圖3所示。

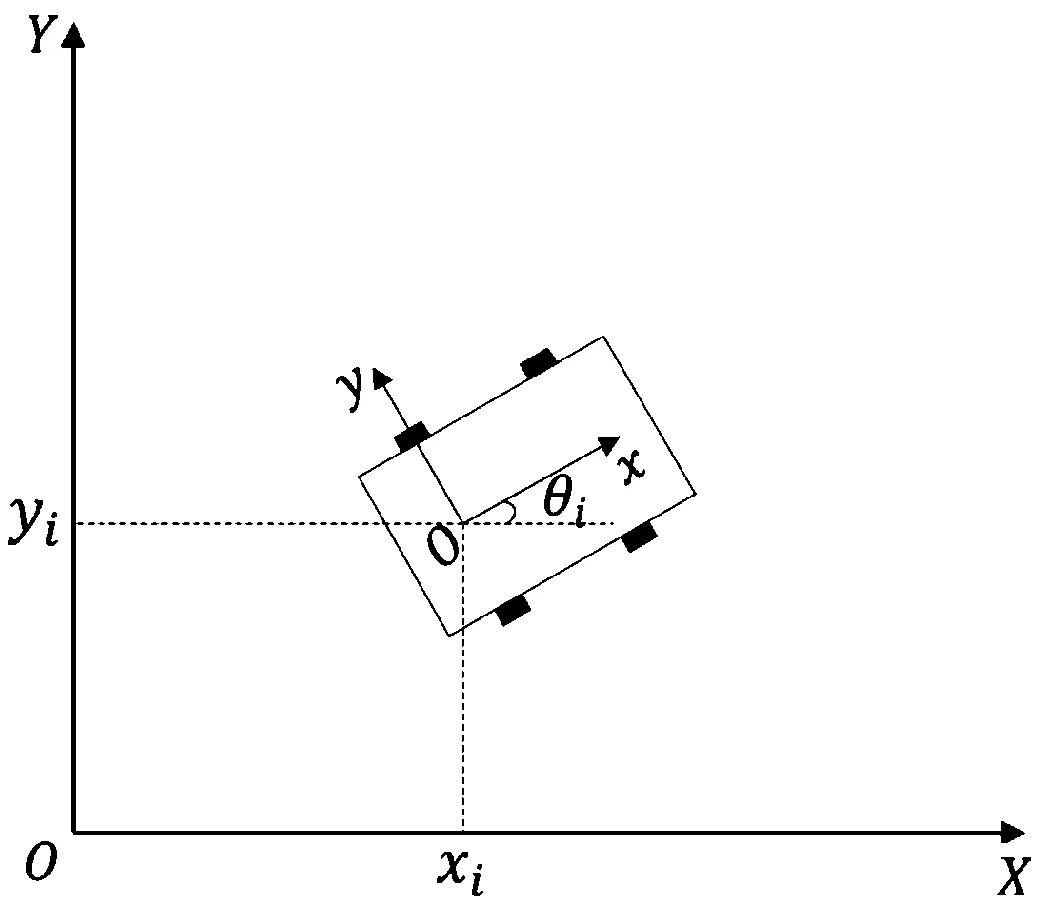
圖3 移動(dòng)小車的運(yùn)動(dòng)學(xué)模型示意圖

移動(dòng)小車位姿模型如圖4所示，實(shí)際位姿坐標(biāo)為(xi,yi,θi)，向前移動(dòng)時(shí)線速度和角速度分別為vi、ωi，小車運(yùn)動(dòng)學(xué)模型為

圖4 移動(dòng)小車位姿模型

(1)

在XOY坐標(biāo)下給定的領(lǐng)航小車期望軌跡位姿坐標(biāo)為(xr,yr,θr)，期望軌跡的線速度和角速度分別為vr和ωr。利用平面坐標(biāo)變換，領(lǐng)航小車的位姿誤差方程為

(2)

對(duì)式(2)進(jìn)行微分，結(jié)合式(1)整理可以得到領(lǐng)航小車位姿誤差微分方程

(3)

為了更好地描述移動(dòng)小車的編隊(duì)控制，建立了如圖5所示的編隊(duì)控制運(yùn)動(dòng)學(xué)模型，其中R1為領(lǐng)航小車，Ri(i={2,3,…,n})為跟隨小車，Rvi為Ri在期望隊(duì)形中的映射小車，線速度和角速度分別為vvi和ωvi。在運(yùn)動(dòng)過程中，R1和Rvi之間的相對(duì)位置用Δi=[Δix,Δiy]∈R2描述。利用平面坐標(biāo)變換，得到跟隨小車的期望位姿

圖5 移動(dòng)小車編隊(duì)控制運(yùn)動(dòng)學(xué)模型示意圖

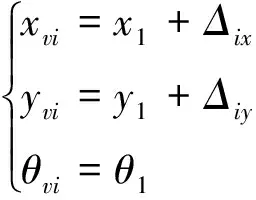
(4)

式中：(x1,y1,θ1)T為領(lǐng)航小車的位姿，(xvi,yvi,θvi)T為跟隨小車Ri(i={2,3,…,n})的期望位姿，則跟隨小車的位姿誤差方程為

(5)

對(duì)式(5)進(jìn)行微分，得

將式(1)代入，可以得到跟隨小車位姿誤差微分方程

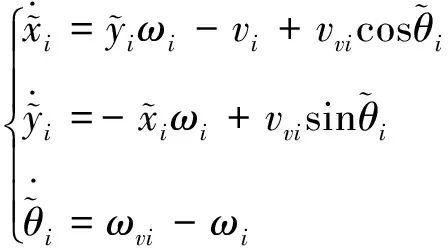
(6)

2.2 多移動(dòng)小車編隊(duì)任務(wù)描述

由n個(gè)輪式移動(dòng)小車組成的領(lǐng)航-跟隨型編隊(duì)系統(tǒng)中，編隊(duì)控制的目的在于調(diào)整各個(gè)小車的位置使系統(tǒng)以特定的幾何圖形移動(dòng)，即跟隨小車和領(lǐng)航小車的線速度和角速度保持一致(即vvi=v1，ωvi=ω1)，并且相對(duì)位置和方向滿足期望的拓?fù)浜臀锢砑s束：

(7)

(8)

(9)

3 控制器設(shè)計(jì)

為了實(shí)現(xiàn)多移動(dòng)小車的編隊(duì)控制和隊(duì)形變換控制，提出了基于有限時(shí)間趨近律的編隊(duì)控制策略，其結(jié)構(gòu)如圖6所示。對(duì)于領(lǐng)航小車，首先根據(jù)式(1)建立小車的運(yùn)動(dòng)學(xué)模型，將當(dāng)前實(shí)際位姿與期望位姿根據(jù)式(2)分析得到位姿誤差并輸入到編隊(duì)控制器中，計(jì)算得到控制小車跟蹤期望軌跡的線速度和角速度。對(duì)于跟隨小車，同樣需要先建立小車的運(yùn)動(dòng)學(xué)模型，再根據(jù)領(lǐng)航小車當(dāng)前實(shí)際位姿和相對(duì)位置Δi=[Δix,Δiy]∈R2計(jì)算得到跟隨小車的期望位姿，最后根據(jù)式(5)分析得到位姿誤差。

圖6 移動(dòng)小車編隊(duì)控制結(jié)構(gòu)框圖

滑模變結(jié)構(gòu)控制具有響應(yīng)速度快、物理實(shí)現(xiàn)簡(jiǎn)單等特點(diǎn)[19-20]，能更好地應(yīng)用于移動(dòng)小車的非線性控制。

引理[19]：對(duì)于任何x∈R且|x|→∞，有φ(x)=xsin(arctanx)≥0，當(dāng)且僅當(dāng)x=0時(shí)“=”成立。

引入反步法，并根據(jù)上述引理設(shè)計(jì)系統(tǒng)滑模切換函數(shù)。

(10)

(11)

根據(jù)以上分析設(shè)計(jì)滑模切換函數(shù)

(12)

為使系統(tǒng)由于切換時(shí)間、空間滯后等因素導(dǎo)致的無法消除的抖振得以削弱，而不影響滑模面趨近速度，采用有限時(shí)間趨近律[21]：

(13)

其中

式中:η>0，0<δ<1，ε>0，fal(s,η,δ)為非連續(xù)線性函數(shù)，δ為fal(s,η,δ)在原點(diǎn)附近正負(fù)對(duì)稱區(qū)間的長(zhǎng)度。當(dāng)|s|<1和|s|≥1時(shí)取不同的參數(shù)k，可使系統(tǒng)在初始階段趨近速度增大，而在趨近滑模面時(shí)降低速度并削弱系統(tǒng)的抖振。

(14)

整理上式可以得到控制律

(15)

4 數(shù)值仿真

為了驗(yàn)證本文所提出的領(lǐng)航跟隨型編隊(duì)控制方法的有效性，分別對(duì)由5個(gè)移動(dòng)小車組成的編隊(duì)進(jìn)行編隊(duì)隊(duì)形控制和隊(duì)形變換數(shù)值仿真實(shí)驗(yàn)，期望編隊(duì)隊(duì)形共有3種，如圖7所示。式(13)中有限時(shí)間趨近律滑模控制參數(shù)設(shè)置為k1=k2=3，δ1=δ2=0.2，η1=η2=0.5，ε1=ε2=0.01。

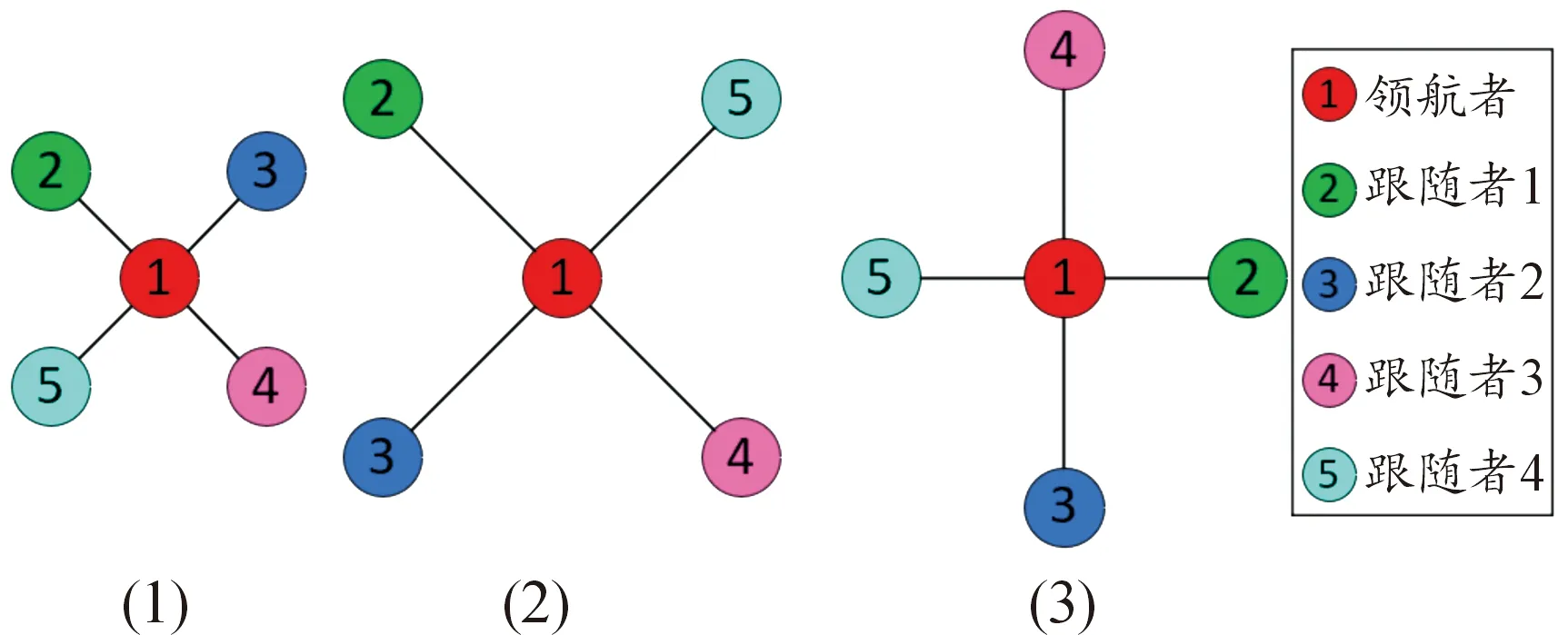
圖7 期望編隊(duì)隊(duì)形示意圖

圖7所示期望編隊(duì)隊(duì)形中，R1和Rvi之間的相對(duì)位置矩陣為

4.1 多移動(dòng)小車編隊(duì)控制仿真

首先采用由4個(gè)跟隨小車和1個(gè)領(lǐng)航小車組成的多移動(dòng)小車系統(tǒng)在Matlab/Simulink下進(jìn)行編隊(duì)控制數(shù)值仿真。

移動(dòng)小車的初始條件如表1所示。

表1 移動(dòng)小車的初始條件

領(lǐng)航-跟隨型編隊(duì)控制任務(wù)分為3個(gè)階段：Ⅰ)0～9.4 s為第一個(gè)階段，期望編隊(duì)隊(duì)形為圖7的(1)，領(lǐng)航者的期望軌跡為直線，期望線速度為vr=4.8 m/s，期望角速度為ωr=0 rad/s；Ⅱ)9.4～25.1 s為第二個(gè)階段，期望編隊(duì)隊(duì)形不變，領(lǐng)航者的期望軌跡為半徑為24 m的圓弧，期望線速度為vr=4.8 m/s，期望角速度為ωr=0.2 rad/s；Ⅲ)25.1～34.6 s為第三個(gè)階段，期望編隊(duì)隊(duì)形不變，領(lǐng)航者的期望軌跡為直線，期望線速度為vr=4.8 m/s，期望角速度為ωr=0 rad/s。仿真結(jié)果如圖8—11所示。

圖8表示5個(gè)移動(dòng)小車系統(tǒng)在各個(gè)運(yùn)動(dòng)時(shí)刻的隊(duì)形，每個(gè)小車用不同顏色的圓圈表示，圓圈中的箭頭表示各移動(dòng)小車的運(yùn)動(dòng)方向。多移動(dòng)小車系統(tǒng)在0、9.4和25.1 s的運(yùn)動(dòng)軌跡開始變化，但在移動(dòng)過程中保持編隊(duì)隊(duì)形不變，5個(gè)小車均可收斂至期望隊(duì)形并沿著期望軌跡運(yùn)動(dòng)。

圖8 移動(dòng)小車編隊(duì)運(yùn)動(dòng)軌跡1

圖9—11分別表示跟隨小車與領(lǐng)航小車航向角、X軸方向和Y軸方向誤差，由于開始時(shí)小車處于靜止?fàn)顟B(tài)，并且每個(gè)小車位置和航向角與期望值均存在一定誤差，因此收斂至期望隊(duì)形用時(shí)較長(zhǎng)，為2.61 s。

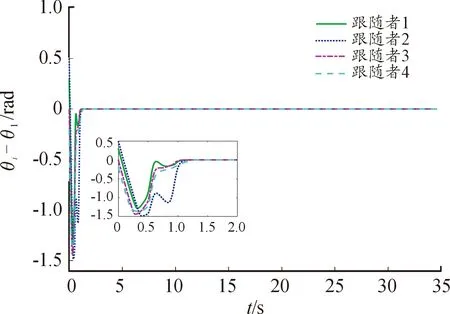
圖9 跟隨小車航向角誤差曲線1

圖10 跟隨小車與領(lǐng)航小車X軸方向距離誤差曲線1

圖11 跟隨小車與領(lǐng)航小車Y軸方向距離誤差曲線1

圖12 干擾下移動(dòng)小車編隊(duì)運(yùn)動(dòng)軌跡1

圖13 干擾下跟隨小車航向角誤差曲線1

圖14 干擾下跟隨小車與領(lǐng)航小車X軸方向距離誤差曲線1

圖15 干擾下跟隨小車與領(lǐng)航小車Y軸方向距離誤差曲線1

由圖12—15可知，12.5～13.5 s加入擾動(dòng)后各跟隨小車的位置和方向都受到了影響，航向角誤差最大值為1.064 rad，與領(lǐng)航小車X軸和Y軸方向距離誤差為1.496 0 m和0.604 3 m。擾動(dòng)結(jié)束后，跟隨小車用時(shí)0.84 s便恢復(fù)了期望隊(duì)形，可見該多移動(dòng)小車編隊(duì)控制方法在編隊(duì)控制時(shí)具有較好的抗干擾性能。

4.2 多移動(dòng)小車隊(duì)形變換控制仿真

同樣采用由4個(gè)跟隨小車和1個(gè)領(lǐng)航小車組成的多移動(dòng)小車系統(tǒng)在Matlab/Simulink下進(jìn)行編隊(duì)控制和隊(duì)形變換控制數(shù)值仿真。

移動(dòng)小車的初始條件如表2所示。

表2 移動(dòng)小車初始條件

領(lǐng)航-跟隨型編隊(duì)任務(wù)分為3個(gè)階段：

Ⅰ)0～15.7 s為第一階段，期望編隊(duì)隊(duì)形為圖7的(1)，領(lǐng)航者的期望軌跡為半徑24 m的圓弧：

期望線速度為vr=4.8 m/s，角速度為ωr=0.2 rad/s；

Ⅱ)15.7～30 s為第二個(gè)階段，期望編隊(duì)隊(duì)形為圖7的(2)，領(lǐng)航者的期望軌跡為半徑32 m的圓弧：

期望線速度和角速度分別為vr=4.8 m/s和ωr=0.15 rad/s；

Ⅲ)30～50 s為第三個(gè)階段，期望編隊(duì)隊(duì)形為圖7的(3)，領(lǐng)航者的期望軌跡不變。

仿真結(jié)果如圖16—19所示。

圖16為5個(gè)移動(dòng)小車系統(tǒng)在各個(gè)運(yùn)動(dòng)時(shí)刻的隊(duì)形，每個(gè)小車用不同顏色的圓圈表示，圓圈中的箭頭表示各移動(dòng)小車的運(yùn)動(dòng)方向。在0、15.7和30 s開始隊(duì)形變換，5個(gè)小車在3個(gè)階段均可收斂到期望隊(duì)形并沿著期望軌跡運(yùn)動(dòng)。

圖16 移動(dòng)小車編隊(duì)運(yùn)動(dòng)軌跡2

圖17—19表示跟隨小車與領(lǐng)航小車航向角、X軸方向和Y軸方向誤差，由于開始時(shí)小車處于靜止?fàn)顟B(tài)，并且每個(gè)小車位置和航向角與期望值偏差較大，第一階段收斂至期望隊(duì)形ΔⅠ用時(shí)較長(zhǎng)，為2.00 s。第二階段編隊(duì)隊(duì)形調(diào)整為ΔⅡ，編隊(duì)隊(duì)形仍為正方形，只是跟隨小車和領(lǐng)航小車在X軸和Y軸方向的距離增大，因此調(diào)整用時(shí)較短，為1.79 s。第三階段編隊(duì)隊(duì)形調(diào)整為ΔⅢ，編隊(duì)隊(duì)形由正方形變換為菱形，由于隊(duì)形變化較大，在隊(duì)形調(diào)整過程中跟隨小車1和4與領(lǐng)航小車航向角誤差偏大，調(diào)整時(shí)間變長(zhǎng)，為1.82 s。

圖17 跟隨小車航向角誤差曲線2

圖18 跟隨小車與領(lǐng)航小車X軸方向距離誤差曲線2

圖19 跟隨小車與領(lǐng)航小車Y軸方向距離誤差曲線2

由圖20—23可知，20～21 s加入擾動(dòng)后各跟隨小車的位置和方向同樣都受到了影響，航向角誤差最大值為0.325 9 rad，與領(lǐng)航小車X軸和Y軸方向距離誤差分別為1.452 5 m和0.582 9 m。擾動(dòng)結(jié)束后，跟隨小車用時(shí)1.59 s便恢復(fù)了期望隊(duì)形，可見該多移動(dòng)小車編隊(duì)控制方法在隊(duì)形變換控制時(shí)同樣具有較好的抗干擾性能。

圖20 干擾下移動(dòng)小車編隊(duì)運(yùn)動(dòng)軌跡2

由圖8—23的實(shí)驗(yàn)結(jié)果可知，本文設(shè)計(jì)的編隊(duì)控制策略能夠有效應(yīng)用于多移動(dòng)小車的編隊(duì)控制和隊(duì)形變化控制中。

圖21 干擾下跟隨小車航向角誤差曲線2

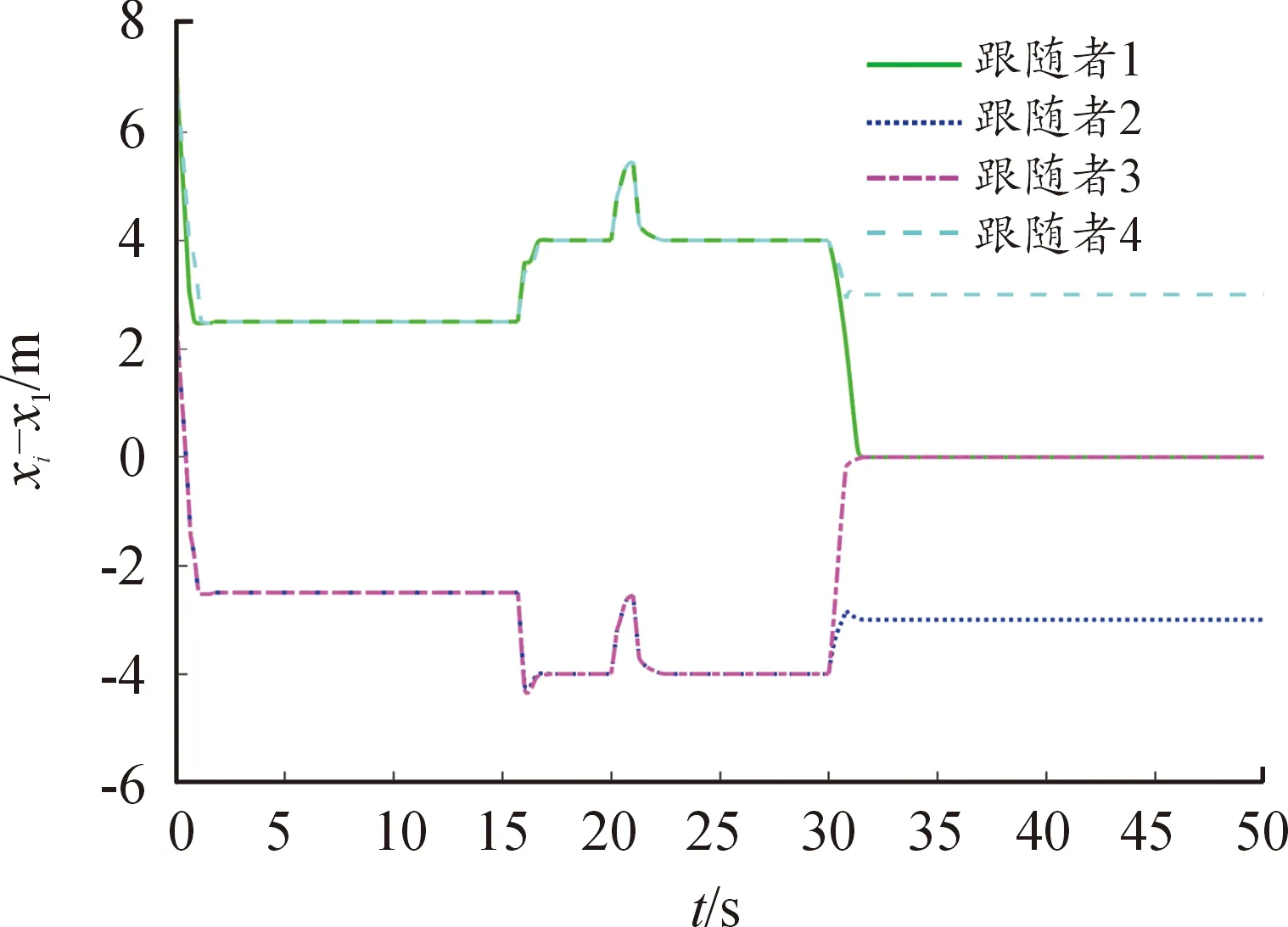
圖22 干擾下跟隨小車與領(lǐng)航小車X軸方向距離誤差曲線2

圖23 干擾下跟隨小車與領(lǐng)航小車Y軸方向距離誤差曲線2

5 結(jié)論

所提出的控制策略能快速實(shí)現(xiàn)隊(duì)形變化，但變化過程角速度較大，導(dǎo)致航向角誤差偏大，后續(xù)可通過改進(jìn)算法，增加時(shí)間、能耗等指標(biāo)，提高適應(yīng)性。