考慮軌跡分析的車輛異常行為辨識

丁 華，楊文杰，姜 超

(江蘇大學 汽車與交通工程學院，江蘇 鎮江 212013)

0 引言

隨著計算機軟件、硬件及視覺技術的快速發展，利用交通視頻監控系統提升道路安全管理水平是現代道路安全的重要保障，而基于車輛運動軌跡的行為分析和識別成為最有前景的發展方向之一[1]。通過監控視頻對車輛進行跟蹤獲取軌跡，并對軌跡進行實時處理和分析，自動檢測道路中車輛的異常行為，如闖紅燈、擅自變道、違章轉向、急剎車、超速行駛和車輛逆行等[2-4]。

研究人員對交通監控中識別運動車輛的異常行為方面取得了一些進展。Johnson等[5]和Sumpter等[6]使用自組織特征映射神經網絡的方法對軌跡空間模式進行建模。Hu等[7]利用模糊自組織映射方法學習目標的運動軌跡和行為模式，實現對異常事件的檢測和判別。楊龍海等[8]提出了基于軌跡數據的車輛異常行為分級檢測算法，使用神經網絡對不同種類的異常行為樣本進行訓練識別。以上基于神經網絡的學習方法網絡設置復雜、學習速度慢，需要大量樣本，對實時性要求較高。Cai等[9]提出了一種異常行為檢測框架，該框架包括軌跡模式學習模塊和異常檢測模塊，軌跡模式學習模塊通過對軌跡聚類并學習方向模式，異常檢測模塊通過建立每類軌跡的HMM模型來對新軌跡進行異常檢測，該方法在訓練時需要提前設定狀態數目，適用于對場景先驗知識比較了解的情況。Athanesious等[10]提出了一種新的基于軌跡聚類方法來檢測車輛異常軌跡，結合譜聚類理論和貝葉斯決策理論將事件分為正常和異常，該方法對實時性要求較高，可以通過深度學習的方法來擴展。Xu等[11]提出了雙模式檢測模型來檢測道路交通中車輛異常運動模式，靜態模式從背景建模中學習，用來檢測在道路中保持靜止的異常車輛。動態模式用來檢測從跟蹤軌跡中偏離主要運動模式的異常行為。該方法檢測誤差低，在低質量的流視頻中有待提升。Piciarelli等[12]提出了一種基于軌跡的聚類方法。異常軌跡通過一系列集群形成的樹提取。異常軌跡是那些與樹相比概率較小的軌跡。通過這種方法可以很容易地識別出在錯誤方向上行駛的車輛，但是這種方法不能估計車輛的速度。李永等[13]提出了基于隨機森林的車輛行為分析方法，該方法通過擬合跟蹤軌跡提取特征值，并將其輸入隨機森林算法分類器中，對車輛行為進行分析，該方法對車輛的特征值提取較少，識別行為單一。黃鑫等[14]提出了基于監控視頻的車輛異常行為檢測方法，該方法通過均值漂移算法對速度和角度兩個運動特征聚類，得到聚類后統計直方圖，由運動特征熵和運動特征標量到聚類中心的歐氏距離來判斷車輛有無異常行為。該方法對動態變化場景中車輛異常行為的檢測效果較差。Hu等[15]提出了軌跡多層次學習框架來識別異常交通行為，使用貝葉斯決策對車輛的異常換道和掉頭行為進行辨識。Wang等[4]分析了復雜場景下常見的車輛異常行為，如異常變道、超速異常、低速異常、逆行等。對于速度異常問題，該方法以簡單的道路規定閾值為判別方法，場景適應性較差。通過以上研究發現，無監督學習成為異常檢測的熱點，該方法不需要軌跡標簽，通過對軌跡自動學習建立正常軌跡模型，與正常軌跡對比來辨識新軌跡是否異常，應用廣泛。在速度異常的檢測中，沒有考慮交通流速度大小和不同車型對速度異常的影響。

本文以車輛運動軌跡為研究對象，提出了一種通過軌跡分析辨識交通異常行為的有效方法。首先對獲取的軌跡采用DP算法[16]進行壓縮，只保留特征點。然后使用改進的Hausdorff距離計算軌跡間的相似度矩陣，采用譜聚類算法學習軌跡空間模式。在此基礎上，對每個空間模式進行中心軌跡提取并利用位移向量學習軌跡的方向模式。利用空間模式和方向模式對新軌跡進行混合匹配來檢測異常行為。對于每類運動模式，通過速度特征提取，取偏離正常運動區間5%車輛的速度為速度異常閾值，對車輛進行實時速度異常檢測。

圖1為異常行為辨識流程圖。

1 軌跡學習

1.1 軌跡預處理

1)軌跡長度篩選。為保持系統的穩定性，提高聚類準確度，需要采用充分長的運動軌跡進行學習，刪除采樣點少的軌跡。

2)軌跡壓縮。為減少軌跡相似性度量的計算，采用道格拉斯—普克算法(DP算法)對軌跡進行壓縮，只保留軌跡的特征點。

1.2 軌跡空間模式學習

軌跡的相似性在運動軌跡聚類中起著非常重要的作用。目前軌跡聚類中的距離度量主要包括基于歐氏距離的方法、基于最長公共子序列的方法、基于動態事件窗口的方法以及基于Hausdorff距離的方法。與其他幾種方法相比，基于Hausdorff距離的方法對于軌跡點集之間的相似性度量更為高效。本文采用改進的Hausdorff[17]距離計算軌跡的空間相似程度。假設軌跡集合中存在2條軌跡A={ai，i=1，2，…，N}，B={bj，j=1，2，…，M}，對于軌跡A上的任意一點ai，在軌跡B上有距離ai最近的點使得：

(1)

那么軌跡AB的空間有向距離則可以表示為：

(2)

式中，NA為A的軌跡點個數。A、B之間的對稱距離為：

(3)

由此可以轉化為A、B的相似度函數:

s(A，B)=exp(-H(A，B)/2σ2)

(4)

式中，σ為尺度參數。如果h(A，B)越小，A、B空間距離越小，相似度越高。

在計算出軌跡間相似度矩陣后，采用譜聚類算法學習車輛軌跡的空間分布模式。利用譜聚類[18]對車輛軌跡進行聚類，步驟如下：

1)對于給定的m條軌跡的集合Traj={T1，T2，…，Tm}，利用改進的hausdorff距離計算軌跡間相似度矩陣，滿足式(5)所示條件。

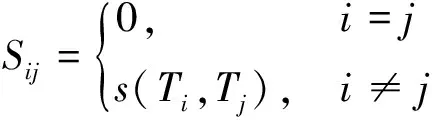
(5)

2)根據相似度矩陣S定義對角矩陣D。對相似度矩陣S中第i行的元素進行求和得到矩陣D的主對角元素Dii，如式(6)所示。

(6)

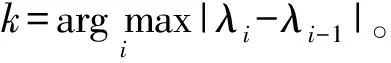
4)選取與最大的k個特征值對應的k個特征向量x1，x2，…，xk，將這k個特征向量按列構造一個m×k的矩陣X=[x1,x2,…,xk]。對X中的每一行做歸一化處理得到一個新的矩陣Y，歸一化公式如式(7)所示:

(7)

5)軌跡樣本中的每一條軌跡Ti都和矩陣Y中的第i個行向量相對應，最后使用k-means聚類算法將矩陣Y聚成k個類。

6)將樣本軌跡中的每一條軌跡按照其在矩陣Y中相對應的行向量的類別進行分配。

1.3 軌跡方向模式學習

1)將軌跡進行空間譜聚類學習后軌跡被有效地劃分為軌跡簇。通過提取各類簇的代表性軌跡來表示該類運動模式，對于第k類的任意一條軌跡Ti計算其與該類中其他軌跡的平均距離：

(8)

式中:nk為第k個分布中的軌跡數量。

選取任意分布k中與其他軌跡平均距離最小的軌跡作為該分布的代表性軌跡，該軌跡代表了該場景下第k個運動模式。

2 目標異常行為檢測

2.1 軌跡空間匹配

對于每個新軌跡點P(x0，y0)，利用中心軌跡的起點和終點確定方程Ax+By+C=0，利用式(9)計算新軌跡點與各個中心軌跡的距離，并將距離從小到大排序，距離最小的代表該點屬于該條中心軌跡所在的運動模式。

(9)

2.2 軌跡方向匹配

一個運動模式代表一個特定的運動方向，當新軌跡的方向與正常運動模式的方向不同時，必然會出現交通異常行為，比如逆行。當第一個軌跡點產生時，首先計算該軌跡點所屬的運動模式，假設第一個點的方向與該運動模式中心軌跡的方向一致，對于其他的跟蹤點(i>1)異常行為檢測的方向判別如下:

(10)

式中：cosθ代表向量A與向量B的余弦相似度，取值在[-1，1]之間，向量A表示每個運動模式的位移向量，向量B表示第i個跟蹤點和第i+1個跟蹤點之間的位移向量。如果第i個點和第i+1個點所在模式不同，則該車發生了變道行為。當cosθ<0時，軌跡與運動模式的方向相反，表示該車輛發生了逆行。

2.3 速度異常檢測

筆者提出的速度異常檢測方法完全依靠道路的歷史數據識別速度軌跡異常的車輛，包括超速異常檢測和低速異常檢測。該方法主要是通過軌跡的空間模式學習得到各類簇后，提取各類簇中每條軌跡的速度特征，統計每條軌跡的速度變化曲線圖，定義95%的行駛車速為正常行駛區間，剩余5%為異常。設置超速行駛和低速行駛的閾值將這些異常的軌跡識別出來。當產生待識別的新軌跡時，以此判斷每個點是否在正常的行駛區間內。如果在正常區間，則說明軌跡正常；如果大于超速閾值，則說明該車超速異常；如果低于低速閾值，則說明該車低速異常。

3 實驗分析

基于HighD[19]數據集中的一個場景做驗證。該場景由雙向6車道構成，車輛的軌跡點通過無人機獲取。原始軌跡共1 047條，去除不完整軌跡和換道軌跡后剩余818條。圖2為軌跡的提取與處理過程，其中圖2(b)顯示了壓縮前后的軌跡對比圖，壓縮前共有32個藍色軌跡點，壓縮后只有6個紅色特征點。

圖2 軌跡的提取與處理

預處理后的軌跡經過hausdorff距離計算出軌跡的相似度矩陣后利用譜聚類算法學習出軌跡的空間分布模式，圖3是軌跡的空間聚類結果。

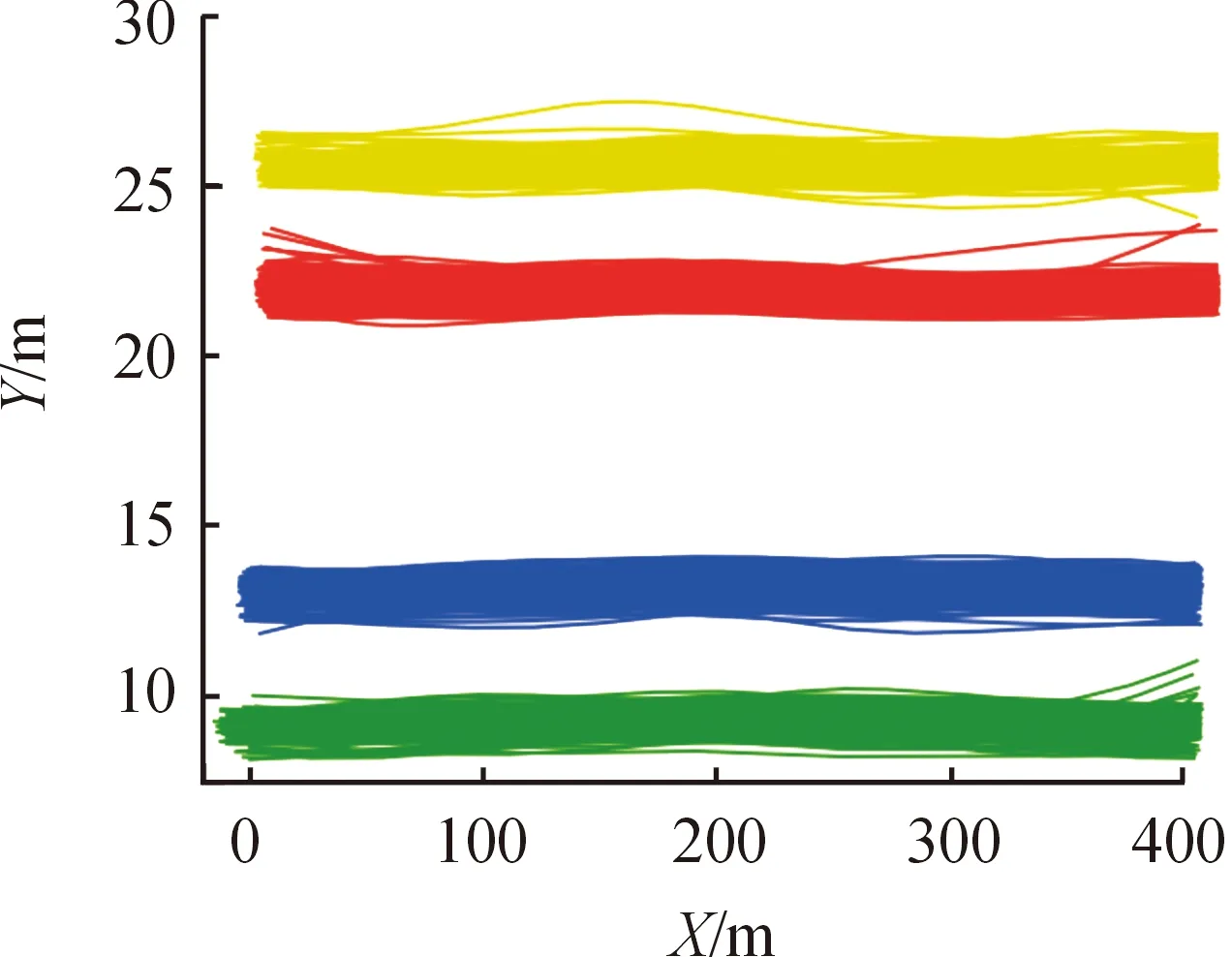
圖3 軌跡空間模式學習

通過空間模式學習表明：軌跡的4種運動模式正好對應道路上4條車道，分別是第2條車道(黃)、第3條車道(紅)、第5條車道(藍)和第6條車道(綠)。然后對軌跡進行方向模式學習，圖4為方向模式學習結果。

圖4 方向模式學習

圖中的曲線代表每個運動模式的中心軌跡，帶箭頭的線段表示該曲線的位移向量。2、3車道的運動模式由右向左，5、6車道的運動模式由左向右。對于逆行軌跡，相鄰軌跡點之間位移向量和所在的運動模式的方向向量的夾角余弦小于0且無限接近-1。對于正常行駛車輛的軌跡，其相鄰軌跡點之間的位移向量與所在模式的方向向量的夾角余弦接近1。圖5表示正常軌跡相鄰點之間位移向量與所在模式方向向量的夾角余弦。

圖5 正常軌跡夾角余弦圖

圖5橫坐標代表的是軌跡點，縱坐標表示相鄰軌跡點之間的夾角余弦，例如第1個柱狀圖代表第1個點和第2個點的方向向量與所在空間模式方向向量的夾角余弦。通過計算相鄰軌跡點之間的方向向量與所在模式的方向向量的夾角余弦，就可以判定車輛是否逆行，只要存在夾角余弦小于0的情況，就可以判斷車輛發生逆行，可以有效地檢測出逆行行為。表1為樣本軌跡空間匹配結果。

表1 軌跡空間匹配

由表1可知，所有軌跡點到車道2中心軌跡的距離最短，所以該軌跡屬于2車道。然后再對其進行方向模式匹配，匹配結果如圖6所示。

圖6 逆行軌跡夾角余弦圖

由圖6可知，該軌跡相鄰兩點之間的方向向量與所在空間模式的方向向量的夾角余弦都小于0且接近-1，該軌跡為逆行軌跡。綜合空間模式匹配結果可知，該軌跡為2車道逆行軌跡。

對于速度異常的車輛通過軌跡的空間模式學習后，提取出各模式軌跡的速度特征，統計每個模式中各個軌跡的速度變化，就可以確定正常車輛行駛的速度區間。將95%的駕駛員行駛的速度區間作為正常行駛區間，剩下5%作為異常行駛的區間。圖7為各車道車型速度分布圖。

圖7中，紅色的曲線代表5%駕駛員行駛的速度異常軌跡，藍色的曲線代表95%的駕駛員行駛的正常軌跡。由于在現實生活中，超速行駛的駕駛員比低速行駛的駕駛員更為常見，取前1%的駕駛員行駛的速度為低速閾值，后4%的駕駛員行駛的速度為超速閾值。圖7(a)中低速異常閾值為79 km/h，超速異常閾值為120 km/h，圖7(b)中低速異常閾值為76 km/h，超速異常閾值為131 km/h，圖7(c)中低速異常閾值為89 km/h，超速異常閾值為144 km/h，圖7(d)中低速異常閾值為82 km/h，超速異常閾值為156 km/h，圖7(e)中低速異常閾值為76 km/h，超速異常閾值為132 km/h。圖7(f)中低速異常閾值為74 km/h，超速異常閾值為90 km/h。通過以上分析可知：在不同的交通場景下，可以根據海量的歷史數據分析出各車道車輛的速度分布區間，確定超速閾值和低速閾值，從而對車輛的速度是否異常進行實時檢測。圖8為車輛實時速度分析曲線圖。

圖7 各車道車型速度分布圖

圖8 車輛實時速度分析

4 結論

根據改進的Hausdorff距離計算軌跡的空間相似度矩陣，利用譜聚類學習軌跡的空間分布模式，提取中心軌跡利用位移向量學習軌跡的方向模式，通過空間模式與方向模式混合匹配解決了道路中異常車輛的軌跡辨識問題。速度特征提取考慮了不同類型車輛對速度軌跡的影響，以5%行駛的區間為異常區間，確定了道路中車輛行駛的速度異常閾值。通過數據集證明該方法能夠實時有效地辨識出方向異常和速度異常的車輛，對提高交通安全具有重大意義。筆者提出的方法也存在不足，只考慮了車輛類型的影響，在接下來的研究中，將加入天氣等環境因素，提升識別效果。