一種改進的串聯機械臂逆運動學問題數值解法

馬建偉，閆惠騰，沈亞彬，張紅園，呂 琦，高 松

(大連理工大學 精密與特種加工教育部重點實驗室，遼寧 大連 116000)

0 引言

串聯機械臂逆運動學問題指根據給定的末端位姿求解對應的各關節角度(位移)值，是串聯機械臂運動控制的基礎[1-2]。自從串聯機械臂問世以來，其逆運動學問題受到廣泛關注，求解方法主要分為解析法和數值法兩類。解析法借助串聯機械臂的幾何結構和代數方法，推導逆運動學問題解析解，計算速度快，計算結果準確，但需要串聯機械臂幾何構型滿足Pieper準則，即3個相鄰關節軸相交于一點或3個相鄰關節軸相互平行[3]。數值法通常將機械臂逆運動學問題看作非線性方程組，并基于迭代方法求解，無需串聯機械臂幾何構型滿足Pieper準則，收斂結果由迭代初始條件決定。近年來，這兩類逆運動學求解方法的研究也隨著機械臂的普及而不斷涌現。

對于自由度小于6的串聯機械臂和滿足Pieper準則的6自由度串聯機械臂的逆運動學問題，求解逆運動學問題的過程比較簡單[3]。Calderon等[4]使用解析法在5自由度機械臂保持末端執行器坐標系中單軸方向不變的情況下，求解給定位姿對應的逆運動學解。應文杰等[5]基于牛頓下山法建立了3自由度機械臂的逆運動數值求解方法。

對于自由度冗余的串聯機械臂和不滿足Pieper準則的6自由度串聯機械臂的逆運動學問題，求解過程則相對比較復雜。在國內學者的研究中，石建平等[6]以機械臂末端位姿誤差最小為目標，將冗余串聯機械臂逆運動學問題轉化為一個等效的最優化問題，并提出一種改進的粒子群優化算法求解，算法具有較高的收斂精度。林陽等[7]將多種群遺傳算法應用于不滿足Pieper準則的一般串聯機械臂逆運動學問題中，提出一種高精度并行計算的逆運動學求解算法，該算法采用動態變異率的變異算子以提高收斂速度，并將位姿分別設為目標函數以保證二者收斂精度一致。董云等[8]針對平面3自由度冗余串聯機械臂的逆運動學問題，提出一種解析法和遺傳算法結合的求解方法，該算法相比單獨的遺傳算法具有計算量小和適應性強的優點。劉松國等[9]提出一種優化的一般6R串聯機械臂逆運動學解析解法，將逆運動學問題中6個基礎方程變形處理，并基于符號運算將目標矩陣從24階降低到16階，提高了算法的計算速度和穩定性。林明等[10]采用自適應的交叉、變異算子，改進了排序方法與遺傳算法，以求解PUMA560機械臂的逆運動學問題。在國外學者的研究中，Husty等[11]利用經典多維幾何構造方法，將6自由度串聯機械臂運動鏈從中間斷為2個3自由度運動鏈，通過分別求解2個3自由度運動鏈以及2個2自由度運動鏈的逆運動學問題，獲得16組能夠使末端執行器達到相同位姿的逆運動學解，其中包含復數解。Erleben等[12]使用精確的Hessian矩陣代替Levenberg-Marquardt(LM)迭代法中近似的Hessian矩陣，迭代求解機械臂逆運動學問題，通過與擬牛頓法和LM迭代法對比，證明了方法具有較快的收斂速度和較強的收斂能力。Sugihara等[13]基于LM迭代法利用迭代方程殘差的平方模量作為參數因子，提出了一種具有高數值穩定性和收斂性能的串聯機械臂逆運動學問題數值解法。綜上，對于求解串聯機械臂逆運動學問題，已有許多學者提出了解決方法，其中不乏一些優秀的數值解法。然而，由于基于智能算法的數值解法計算過程復雜，計算量大，迭代法仍是最常見的數值解法。但是，常用數值迭代法如牛頓迭代法、共軛梯度法等，收斂速度較慢，且合適的迭代初始值難獲取，致使常規基于迭代法的數值解法在實際計算過程中，仍存在收斂速度慢、易出現不收斂的問題，影響算法魯棒性。

為解決上述問題，提出了一種改進的串聯機械臂逆運動學問題數值解法。創新將LM迭代法中每一迭代步的參數因子μ由當前迭代步對應的微分運動向量的二范數確定，并額外設置步長因子用于以提高每一迭代步的迭代步長。提出的方法顯著提高了算法的收斂速度和收斂能力，有效彌補了常規的數值法魯棒性不足的缺點。

1 常規的數值解法

以圖1所示的6自由度串聯機械臂為例，首先介紹常規的數值法求解逆運動學問題的計算過程。按照式(1)計算6自由度串聯機械臂正運動學問題。

圖1 串聯機械臂

(1)

式中: 關節0為基坐標系，n為末端關節坐標系；ηx、ηy、ηz分別為末端關節坐標系n的xn軸與基坐標系的x0、y0、z0軸的夾角余弦值；ox、oy、oz分別為末端關節坐標系n的yn軸與基坐標系的x0、y0、z0軸的夾角余弦值；ax、ay、az分別為末端關節坐標系n的zn軸與基坐標系的x0、y0、z0軸的夾角余弦值；px、py、pz為末端關節坐標系n原點在基坐標系中的笛卡爾坐標。

6自由度串聯機械臂正運動學問題表達式還可由旋轉和平移組合變換表示，即：

0T6=Trans(px,py,pz)Rot(z,rx)Rot(y,ry)Rot(x,rz)=

(2)

式中:crx、cry、crz、srx、sry、srz分別是cosrx、cosry、cosrz、sinrx、sinry、sinrz的簡寫，Trans(px,py,pz)表示末端關節坐標系沿基坐標系的x0、y0、z0軸平移px、py、pz距離，Rot(z,rx)Rot(y,ry)Rot(x,rz)表示末端關節坐標系先繞著基坐標系z軸旋轉rz角，再繞基坐標系y軸旋轉ry角，再繞著基坐標系x軸旋轉rx角。

聯立式(1)和(2)，得到各關節轉角θi(i=1,2,3,4,5,6)與旋轉角度rx、ry、rz和平移距離px、py、pz之間的關系式，即：

(3)

(4)

在迭代計算過程中，待求解逆運動學問題的機械臂末端位姿記為Tend，末端位姿對應的逆運動學解記為θend，當前迭代步對應的逆運動學解記為θcur，迭代步逆運動學解對應的機械臂末端位姿記為Tcur。上述定義確定后，則按照如下步驟計算給定末端位姿的逆運動學問題。

① 由Tend和Tcur按照式(5)計算當前迭代步微分算子Δcur。

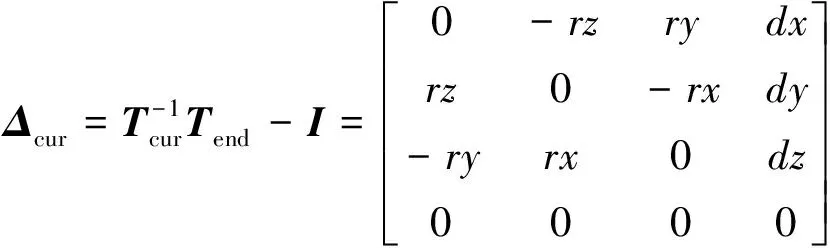
(5)

② 計算當前迭代步逆運動學解θcur對應的雅可比矩陣J，并按照式(6)計算當前迭代步搜索方向。

(6)

式中：μ為參數因子，其數值需預先設定，且數值大小在步驟③中按照迭代結果自適應地改變。引入參數因子μ的目的，為了防止當JTJ接近奇異時dθ過大，從而影響迭代算法的收斂能力。隨后，將θcur與dθ相加得到新的逆運動學解θnew，再利用正運動學計算新的逆運動學解對應的末端位姿Tnew。

③ 由Tend和Tnew按照式(5)計算新的微分算子Δnew，并從中確定新的微分運動向量Dnew，并比較當前迭代步微分運動向量Dcur與新的微分運動向量Dnew的二范數大小。若||Dnew||2<||Dcur||2，則接受新的逆運動學解θnew，令μ=μ/2，θcur=θnew，Dcur=Dnew，返回步驟①進行下一次迭代；若||Dnew||2≥||Dcur||2，則拒絕新的逆運動學解θnew，令μ=2μ，返回步驟①進行下一次迭代。

重復步驟①～③，直到當前迭代步微分運動向量Dcur的二范數小于迭代精度e，算法收斂，得到機械臂末端位姿Tend對應的逆運動學問題的一個解θend。或者迭代次數超出設定上限，算法未能在規定迭代次數內收斂，未能得到滿足迭代精度的機械臂逆運動學解。

2 改進的數值解法

同樣以圖1所示的6自由度串聯機械臂為例，提出一種改進的串聯機械臂逆運動學問題數值解法，改進的數值法流程圖見圖2。

圖2 改進的數值法流程框圖

具體計算過程如下：

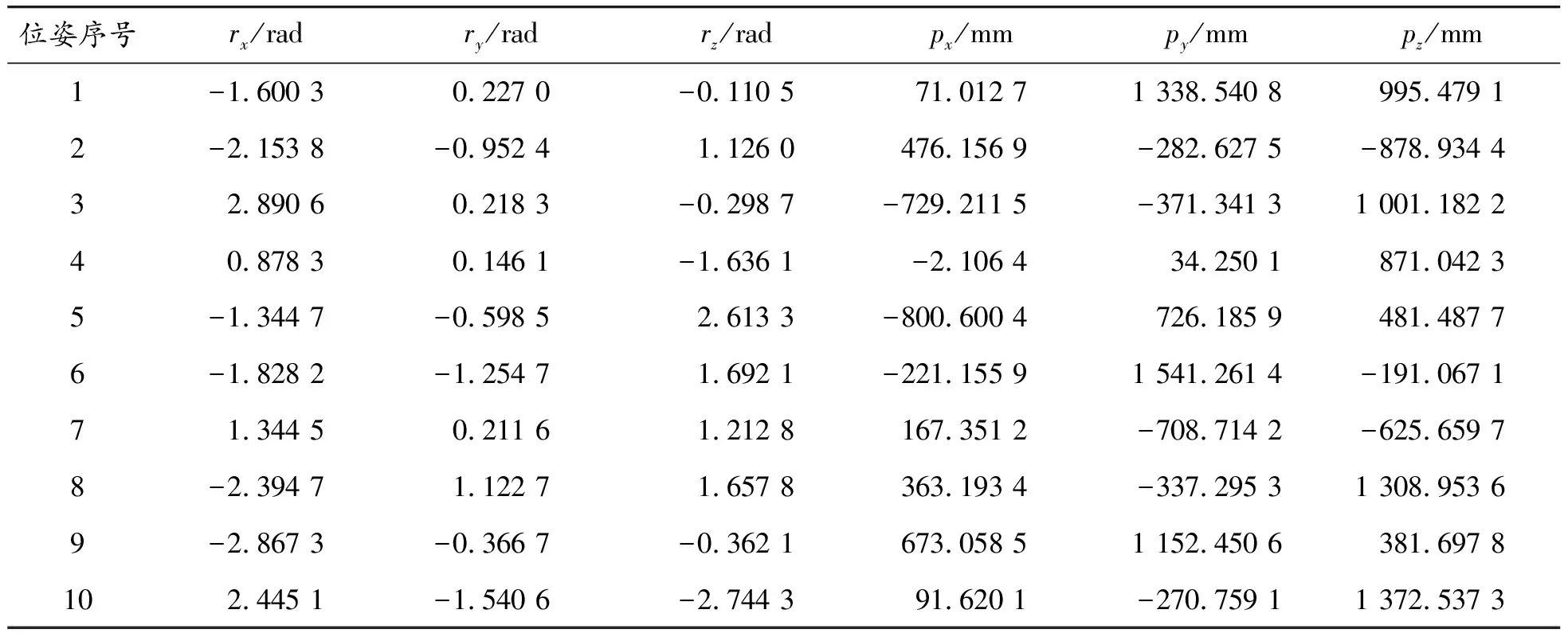
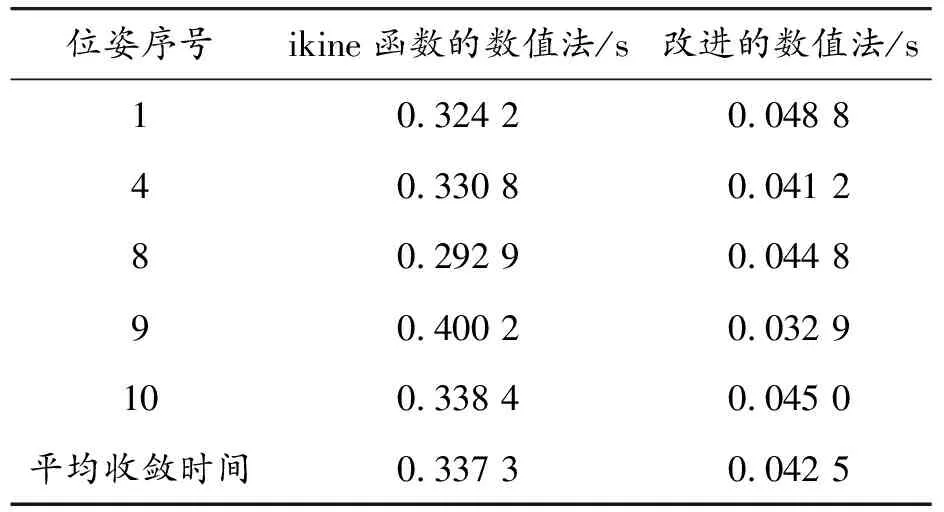
① 由Tend和Tcur按照式(5)計算當前迭代步微分算子Δcur，并由微分算子Δcur確定當前迭代步微分運動向量Dcur。判斷當前迭代步微分運動向量Dcur的二范數是否小于迭代精度e。若||Dcur||2

② 創新將LM迭代法中每一迭代步的參數因子由當前迭代步對應的微分運動向量的二范數確定，并額外設置步長因子以提高每一代步的迭代步長，即按照式(7)計算參數因子μ。

μ=λ||Dcur||2

(7)

其中，λ為步長因子，是小于1的正參數，其數值越小，當前迭代步在搜索方向上步長越大，算法收斂速度越快。但λ不能太小，過小的λ反而會減慢算法的收斂速度。從經驗角度，λ需根據具體問題在1×10-3～1×10-2靈活設定。然后，計算當前迭代步逆運動學解θcur對應的雅可比矩陣J，并按式(6)計算當前迭代步搜索方向dθ。

③ 將θcur與dθ相加得到新的逆運動學解θnew，再利用正運動學計算新的逆運動學解對應的機械臂末端位姿Tnew。在改進的數值法中無需通過比較自適應地調整參數因子μ的值，直接令Tcur=Tnew，θcur=θnew，返回步驟①進行下一次迭代。

重復步驟①～③，直到當前迭代步微分運動向量Dcur的二范數小于迭代精度e，算法收斂，得到串聯機械臂末端位姿Tend對應的逆運動學問題的一個解θend。或者迭代次數超出設定上限，算法未能在規定迭代次數內收斂，未能得到滿足迭代精度的逆運動學解。需要說明的是，改進的串聯機械臂逆運動學問題數值解法理論上是全局收斂的，但迭代收斂的過程與初始條件有關，為避免較長的迭代過程，需要設置迭代次數上限。

通過對比可以看出，常規的數值法和改進的數值法均使用了LM迭代法。不同的是，常規的數值法中參數因子μ按照每一次迭代結果自適應地改變，而改進的數值法基于當前迭代步對應的微分運動向量的二范數確定參數因子μ，這使得迭代算法的收斂速度和收斂能力顯著提高[14-15]。

3 實驗研究

通過實驗驗證改進的數值法的有效性。實驗對象為圖1所示的6自由度串聯機械臂，其幾何參數和關節旋轉范圍如表1、2所示。實驗是在Intel i5-10400F 2.9 GHz CPU和16Gb RAM的Windows系統下Matlab中進行的。

表1 6自由度串聯機械臂改進DH參數

表2 6自由度串聯機械臂各關節旋轉范圍

Matlab Robotics Toolbox包含了豐富的機器人運動學庫函數，其逆運動學求解函數正是基于雅可比偽逆矩陣的原理，使用LM迭代法進行求解[16]。按照改進的DH參數法確定的各關節連桿幾何參數，在Matlab中借助robotics工具箱建立6自由度串聯機械臂數學模型，并由工具箱提供的函數(fkine函數)計算機械臂正運動學問題。其中，θ為連桿夾角，d為連桿距離，a為連桿長度，α為連桿扭角。都是機械臂各關節連桿幾何參數。偏置為建模輔助參數，代表了改進DH參數法定義的關節零位(各關節連桿夾角θi均為0)與SR20A機械臂關節零位(各關節轉角均為0)之間的偏差。

在驗證過程中，首先在6自由度串聯機械臂工作空間范圍內隨機生成10個末端位姿，如表3所示。形式滿足式(2)中的旋轉和平移組合變換。

表3 隨機生成的末端位姿

從表4中可以看出，在使用Matlab Robotics Toolbox中ikine函數的數值解法計算10個機械臂末端位姿逆運動學問題的過程中，在其中5個機械臂末端位姿處算法未能在迭代次數上限內，收斂到一個滿足迭代精度的機械臂逆運動學解，則收斂能力為50%。而在使用改進的數值法計算10個機械臂末端位姿逆運動學問題的過程中，在9個末端位姿處算法均能在迭代次數上限內收斂到一個滿足迭代精度的逆運動學解，則改進的數值法收斂能力為90%。因此，改進的數值法相比于ikine函數的數值法，算法的收斂能力提升了1.8倍。

表4 2種數值法的收斂能力

在2種數值法均能夠收斂的末端位姿處，對2種數值法的收斂速度進行了比較，結果如表5所示。在這些末端位姿處，2種算法收斂過程如圖3所示。

表5 2種數值法的收斂速度

圖3 2種數值法微分運動向量二范數下降速度

從表5中可以看出，在2種數值法均能夠收斂的6自由度串聯機械臂末端位姿處，ikine函數的數值法的平均收斂時間為0.337 3 s，而改進的數值法的平均收斂時間為0.042 5 s。因此，改進的數值法相比于ikine函數的數值法，算法的收斂速度提升了7.9倍。此外，從圖3中也可以直觀地看出，改進的數值法在計算過程中作為迭代結束依據的微分運動向量二范數||Dcur||2下降更快，迭代次數更少，收斂速度提升顯著。

4 結論

針對常規的多軸串聯機械臂逆運動學數值解法存在的收斂速度慢、易出現不收斂等問題，基于LM迭代法提出了一種改進的多軸串聯機械臂逆運動學數值解法。本方法在常規數值解法的基礎上，創新將LM迭代法中每一迭代步的參數因子由當前迭代步對應的微分運動向量二范數確定，進一步提升迭代步搜索方向的準確性，并額外設置步長因子以提高每一迭代步的迭代步長。

實驗結果表明，提出的基于當前迭代步微分運動向量二范數計算參數因子的改進的數值法，相比與Matlab Robotics Toolbox中ikine函數的數值解法，無論在收斂能力還是收斂速度上，都有顯著提升，有效解決了數值法魯棒性不足的問題，能夠在解析法無法應用的場合中快速穩定求解多軸串聯機械臂逆運動學問題。