疫情影響下的應急物資供應鏈與政府調控措施
趙古月
(上海交通大學 安泰經濟與管理學院,上海 200030)
2020年初一場席卷全球的新冠肺炎疫情,對全球商品的供應和需求產生了深遠影響。在疫情發生之初,以口罩和醫療物資為代表的應急物資需求暴漲,同時由于疫情導致區域封閉,原材料供應和員工復工困難,導致供給端產能不足,應急物資供不應求,帶來了價格的急劇上漲,對社會防疫形勢和人民生命健康安全和福利都造成了負面影響。面對疫情對應急物資供應鏈帶來的沖擊,政府調控措施的介入可以增大應急物資的供應,保障全民防疫工作的開展。本文對疫情下應急物資供應鏈進行建模,求解得出的結果反映出,應急物資供應商的利益最大化與社會福利最大化存在沖突的可能性,將政府調控措施加入模型后,可以實現社會福利的最優化。本文通過模型求解和算例分析,比較了不同條件下,不同的政府調控措施對于社會福利的優化效果,并給出了調控建議。
許多學者已經對類似新冠肺炎疫情的突發事件對供應鏈的影響和管理措施進行了研究,Clausen等人最早提出對于供應鏈突發事件的應急管理(disruption management)概念。之后許多學者在供應鏈應急管理方面進行了多方面的研究。Snyder等人對以供應鏈應急管理和不確定性為研究課題在OR/MS上發表的180篇論文進行了文獻綜述,總結出目前對于供應鏈應急管理的研究方向主要包括六個,即供應鏈擾動的影響、戰略決策、采購決策、合同與激勵措施、庫存與設施選址。Paul等人在2016年把供應鏈擾動分為了生產、供應、需求和運輸中的不確定性。
目前對于供應鏈應急管理的研究,很多涉及發生需求擾動或存在擾動可能時供應鏈的協調機制。Qi、Bard和Yu在2004年研究了對于價格線性的需求發生擾動時,單供應商-單零售商的供應鏈協調機制問題,發現由于更改費用的存在,生產計劃存在一定魯棒性,并利用數量折扣契約來使供應鏈整體利益最大化。Xu等人將模型推廣到了需求對價格呈非線性變化的情況;Xiao等人將數量折扣契約模型推廣到了需求發生擾動的單供應商-雙競爭零售商供應鏈;而Chen等人又進一步推廣到了一個供應商、一個占主導地位的零售商,以及多個其他零售商組成的供應鏈。Huang、Yu等人2006年對供應鏈需求擾動情況下供應商-零售商分別決策和聯合決策進行了建模,他們設定原有需求為價格的確定性指數函數,并在原有需求上添加一個需求擾動,以求解不同擾動下供應鏈協調與博弈機制。于輝等人在數量折扣合約的基礎上,探討了回購合約對供應鏈突發需求變化的協調機制。
在供應鏈應急管理的相關研究中,目前對于政府應對措施的相關研究還比較少,而政府措施在類似新冠肺炎疫情這種對供應鏈影響非常大的突發事件中是很重要的,也是本文想要探討的方向。之前的研究也關注過其他相關自然災害的應急物資供應鏈問題,王熹徽和梁樑研究了政府救災物資供應鏈的采購策略和契約協調機制,發現對于應急物資,如果事前采用期權契約機制,能夠大大減少損失。將政府決策措施加入供應鏈應急協調機制中,與供應商和零售商形成博弈,影響供應鏈決策并實現社會福利的最大化,是本文的創新之處。
1 無政府措施時的供應鏈建模
考慮一個單供應商、單零售商的供應鏈模型,供應商根據零售商的訂貨進行生產并給出批發定價,零售商決定面向消費者的零售價格,終端消費者的需求是關于價格的線性函數。供應商的成本包括基礎的人力、材料成本和固定成本,在疫情這樣的特殊情景下,考慮供應商有一定的產能瓶頸限制,在超過產能限制進行生產后,會有額外的附加人力成本。零售商的成本為固定成本。模型中涉及的變量與定義如表1所示。

表1 模型中的變量及含義
在沒有疫情的情況下,消費者的需求為關于價格的遞減線性函數,當疫情發生時,考慮需求受到疫情的影響有一個正向的擾動,假設擾動項為c·sn,即
Q=a-b·p+csn
(1)
其中,a-b·p為價格在p時原有的線性需求,c為商品需求對疫情的敏感系數,n為敏感指數,s為疫情的嚴重程度。
供應商和零售商都以自己的利潤最大化為目標,分別決策批發價格和零售價格:
πA=wQ-mQ-δ·max(0,Q-q)-fA;s.t.w>0
(2)
πB=(p-w)·Q-fB; s.t.p>w
(3)
其中,δ·max(0,Q-q)為需求大于產能限制時,多生產的商品所需的額外人力成本。
生產商和零售商的決策構成一個兩階段的斯塔克伯格博弈,求解該模型得到的優化結果如表2所示。

表2 兩階段斯塔克伯格博弈模型求解結果
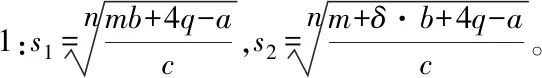
注釋2:當(m+δ)·b+4q-a≤0,即q≤(a-(m+δ)·b)/4時,供應商只存在第三種生產狀態。
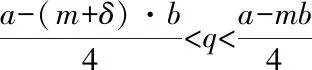

通過求解結果可以看出,當供應商原來的產能小于一個臨界值的時候,不管有沒有疫情,供應商都會選擇加班生產。不管供應商原來的產能多大,當疫情嚴重到一定程度的時候,供應商都會在超出產能的狀態下加班生產。
當供應商的生產處于狀態一和狀態三時,生產材料和人工成本的增大,會導致批發價格和零售價格增大,但零售價格的增量是批發價格增量的一半,即當疫情導致生產成本增大時,零售商毛利的損失會大于消費者利益的損失;而當供應商的生產處于狀態二時,批發價格和零售價格都不受供應商成本變化的影響。
當供應商的生產處于狀態二,即以最大產能生產但不加班時,此時疫情若加重,供應商選擇不擴大產量,而繼續提升批發價格,同時也導致終端零售價格提高,在這種情況下,更多的應急物資需求沒有被滿足,這對社會疫情的防控是不利的,也體現出了此時企業利益與社會利益的不一致問題。
為了減少疫情對于應急物資供應鏈的影響,政府需要實施一些措施來保障物資的充分供應,因此政府的決策需要加入模型中,對供應商和零售商的決策產生影響,形成一個政府-供應商-零售商三階段博弈模型。
2 加入政府決策后的三階段斯塔克伯格博弈模型
在普通的社會福利函數中,通常考慮將消費者剩余和生產者剩余相加,得到社會總剩余以代表對社會的福利。在疫情防控應急物資供應鏈中,這一目標需要做一定的調整,政府需要考慮保障應急物資的供應,若部分應急物資沒有得到有效的供應,對整個社會的福利可能會產生較大的影響。假設每一單位沒有滿足的應急物資需求對社會總福利的損失為β,如當社會上的口罩需求沒有被滿足時,政府需要花費額外成本去應對其負面影響。在政府的目標函數中,在原有社會總剩余的基礎上,需要加入對沒有滿足的需求部分的懲罰項。假設這一指標為H,即
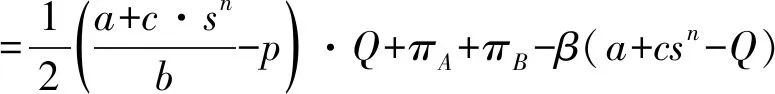
(4)
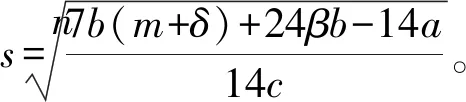
一般來說,應急物資沒有得到滿足時,對于社會福利的影響是足夠大的。在狀態二時,社會福利很有可能是會隨著疫情嚴重程度單調遞減的,也印證了之前的判斷,即供應商在不擴大生產規模的同時提高批發價格,對于社會福利是不利的,所以需要政府措施的介入來調整。在后續章節中,分別采用給供應商補貼、給零售商補貼和調用公共物資三種不同措施,通過建模分析在三種不同調控措施下政府的最優決策,并進行對比。
在模型中加入政府調控措施后,假設政府目標函數為G,政府決策優化模型為
Max.G=消費者剩余+生產者剩余-未滿足需求的懲罰-政府支出
s.t. 政府支出≤I
(5)
其中,I為政府支出的限額。
2.1 給供應商補貼
政府可采取的第一種措施是給予供應商補貼。假設供應商每賣出單位產品,政府給予補貼t,此時三階段的斯塔克伯格博弈模型如表3所示。當政府支出限額足夠大時,求解結果見表4。

表3 政府給供應商補貼后的三階段博弈模型

表4 政府給供應商補貼時,政府、供應商和零售商的決策
由優化結果可見,當調控前供應商的狀態處于狀態一和狀態三時,政府給供應商一定的補貼,可以使得整個社會的福利最大化,且補貼的多少需要根據供應商的實際生產狀態和狀態之間的切換具體確定。當調控前供應商的狀態處于狀態二時,在一定的條件下,有可能出現政府無須給供應商補貼的情況,即保持原狀就能達成社會福利最優。
2.2 給零售商補貼
政府可采取的第二種措施是給予零售商補貼。假設零售商每賣出單位產品,政府給予補貼t,此時三階段的斯塔克伯格博弈模型如表5所示,求解結果見表6。

表5 政府給零售商補貼后的三階段博弈模型

表6 政府給供應商補貼時,政府、供應商和零售商的決策
此時,模型求解結果中,除w*有增加外,其余t*、p*都與措施一是一樣的,而w*的增大,也并沒有導致零售商的利潤減少。所以,在單供應商、單零售商的供應鏈模型中,政府給予零售商補貼和給予供應商補貼的效果是一樣的,補貼收益會在供應商和零售商之間自動進行分配。
2.3 調用公共物資
為了應對疫情影響下的應急物資供應問題,政府還可以選擇調用公共物資,或從其他地區調用物資,再以成本價賣給消費者,未滿足的消費者需求再由零售商去供給。在這種措施下,政府可以理解為一種與現有零售商競爭的應急物資供給商,兩者同時去滿足消費者需求,且政府具有價格的優勢。
假設政府調用的物資數量為Q′,調用單位物資的費用為v,以低價d賣給消費者,Q″為零售商供應的量,此時三階段的斯塔克伯格博弈如表7所示,求解結果見表8。

表7 政府調用儲備公共物資后的三階段博弈模型
政府的決策很大程度上決定于單位物資調用費用,如果調用費用過高而疫情不太嚴重時,政府采取不調用物資而由市場完全供給的方式;而當疫情足夠嚴重時,不管調用費用多高,政府都會采取調用物資的策略。最優調用物資數量根據不同的條件會有變化,即不一定是最大投資限額下的調用數量。

表8 政府調用公共物資時,政府、供應商和零售商的決策
3 算例分析
假設某疫情防控應急物資的需求為Q萬個,Q=10-0.1*p+0.2*sn,應急物資的制造成本為1元/個,加班狀態下需要額外付出3元/個的成本,供應商產能為10萬個,供應商和零售商的固定成本分別為100萬元和10萬元,政府采取調用物資的方式時售價為10元/個。
當應急物資需求沒有滿足時懲罰系數β=10,求解政府調用儲備物資成本分別為10~40元/個時,隨著疫情嚴重程度從小到大,不采取措施、采取補貼供應商/零售商的措施、采取調用公共物資的措施下社會總福利的大小,結果如圖1所示。

(a)v=10 (b)v=20
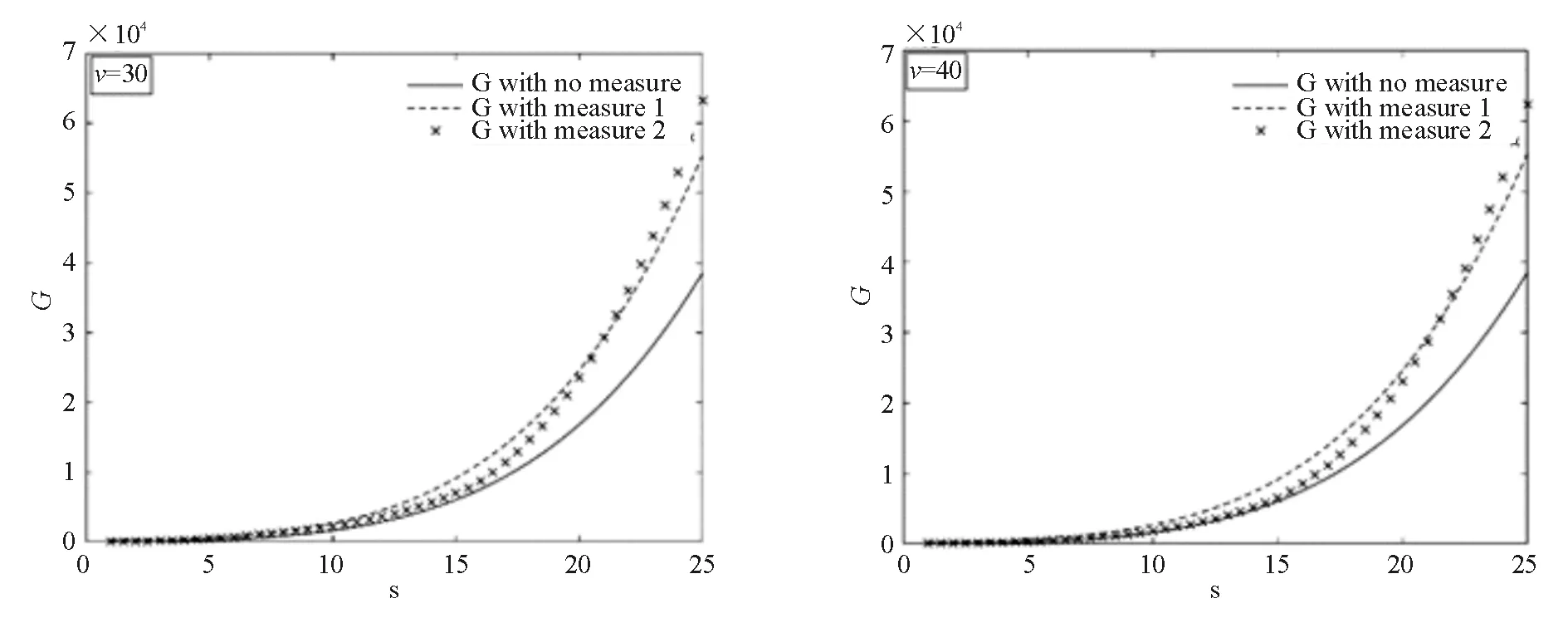
(c)v=30 (d)v=40
當調用物資成本v=10時,不管疫情多嚴重,采取調用物資的方式都優于采用給予供應商/零售商補貼的方式;當v=20時,當s<13,即社會最大需求量小于43.8萬時,采取調用物資的方式更優,當13
當疫情嚴重程度s=10時, 求解β分別為10、50、100、200時,調用物資費用v從小到大時,不采取措施、采取補貼供應商/零售商的措施、采取調用公共物資的措施下社會總福利的大小,結果如圖2所示。

(a)β=10 (b)β=50
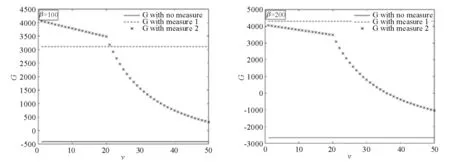
(c)β=100 (d)β=200
當疫情嚴重程度固定時,物資調用成本v越小,措施二越傾向于更優,v越大,措施一越傾向于更優,即兩種措施之間的優劣對比存在一定的臨界值v,且β越大,這個臨界值越小。當β足夠大時,措施一總是優于措施二,即需求未被滿足時的社會福利懲罰足夠大時,不管政府調用物資的成本多低,政府都傾向于采取給予供應商/零售商補貼的方式。
4 總結
本文探討了受疫情影響需求增長的應急物資供應鏈問題,發現了在特定情況下,企業利益與社會利益存在沖突,政府措施的介入可以減少這種沖突,使得應急物資的供應得到保障。本文討論了政府給予供應商補貼、給予零售商補貼和調用儲備公共物資三種措施,求解了三種措施下政府的最優決策以及最優決策下的社會福利。通過模型求解,發現在單供應商-單零售商的供應鏈中,政府給予供應商補貼和給予零售商補貼的效果是相同的,補貼收益會在供應商和零售商之間自主分配。通過算例研究,得出調用物資成本越低、疫情越嚴重,采取調用公共物資的方式越有利;當應急物資的需求不被滿足的后果很嚴重時,不管調用物資的成本多低,政府都應該傾向于采取給予供應商/零售商補貼的方式。

