5G系統對大規模NGSO衛星系統干擾分析等效建模方法

李靈慧, 李 偉, 靳 瑾, 匡麟玲

(1. 清華大學北京信息科學與技術國家研究中心, 北京 100084; 2. 清華大學電子工程系,北京 100084; 3. 國家無線電監測中心, 北京 100041)

0 引 言

衛星網絡的發展初期旨在為偏遠地區提供通信,地面網絡則主要在人口分布密集的地區提供通信。隨著技術不斷發展,越來越多的大規模非靜止軌道(non-geostationary orbit,NGSO)衛星互聯網星座計劃被提出,如衛星總數約為42 000顆的Starlink星座、衛星總數為47 844顆的OneWeb星座、包含3 236顆衛星的Kuiper星座等。到目前為止,衛星互聯網已能夠實現全球大尺度的無縫覆蓋。與此同時,地面網絡的網絡覆蓋廣度和深度也在逐漸提高。

根據國際電信聯盟(International Telecommunication Union, ITU)無線電規則中的業務頻段劃分,在全球范圍內,地面移動業務和衛星固定業務均使用Ka、Q/V頻段,系統頻段在24.75～25.25 GHz、27～29.5 GHz、37.5～43.5 GHz等多個頻段存在重疊,因此需要考慮系統間相互干擾的問題。

3G、4G網絡主要使用中低頻,可能與衛星系統存在干擾的地面移動業務主要為使用毫米波的IMT-2020(5G)系統。考慮到宏蜂窩多采用中低頻,室內熱點位于建筑物內,建筑物損耗較大,對衛星系統干擾較小。因此,與衛星系統產生干擾的IMT-2020系統主要部署場景為室外的城市微蜂窩場景。

根據當前多個典型NGSO衛星系統頻率申報情況,如Starlink、OneWeb、Telesat等,與各國IMT-2020系統的頻率分配情況,NGSO衛星系統在上行鏈路、下行鏈路方向與IMT-2020系統之間都存在頻率重疊。

NGSO衛星系統上行鏈路與IMT-2020系統同頻主要在Ka頻段。目前,SpaceX公司的星鏈互聯網服務正在加速向全球覆蓋邁進,SpaceX已獲得在美國、加拿大和英國等多個國家提供服務的許可證,在許多其他國家的申請進程也正順利推進。美國聯邦通信委員會(Federal Communications Commission,FCC)批準了SpaceX在美6個州從2020年7月開始測試運行Starlink地面基站。測試基站向Starlink衛星上傳數據時,使用頻段包含28.6～29.1 GHz。與此同時,Ka頻段的27.5～29.5 GHz(28 GHz)范圍被部分國家和地區視為5G系統的候選頻段。例如:2018年6月,韓國SK電信通過拍賣獲得28.1～28.9 GHz頻段的5G頻譜使用權,并于2018年12月宣布在部分地區商用5G;2020年12月,澳大利亞通信和媒體管理局宣布將27.5～29.5 GHz頻段作為5G毫米波頻譜,并將該頻譜同時分配給了地面網絡公司和包含Starlink在內的衛星公司。若Starlink系統服務這些國家,則有可能與這些國家的5G設備相互干擾。

NGSO衛星系統下行鏈路和IMT-2020系統同頻主要是在Q/V頻段。Starlink、OneWeb、Telesat等星座的衛星數據庫中均申報了37.5～42.5 GHz頻段,并向FCC提出使用上述頻段的申請。對于5G系統,2019年世界無線電通信大會決定全球范圍內將37～43.5 GHz(40 GHz)頻段標識用于5G及國際移動通信系統未來發展。但由于不同國家的5G系統與衛星系統的頻率劃分不同,衛星系統和5G系統之間可能存在潛在干擾。

現有研究中針對衛星系統間、5G系統和地球靜止軌道(geostationary orbit,GSO)系統間干擾研究較多,但5G系統和NGSO系統之間研究較少。文獻[16]中仿真了5G系統對于GSO衛星以及GSO衛星系統地球站對于5G系統的干擾,依據全球城市人口數量等方法計算等效干擾。文獻[17]針對5G系統對于GSO衛星干擾建模,先計算局部區域的集總干擾,再根據面積占比以及城區因子和熱點因子,計算出衛星點波束覆蓋范圍內所有5G系統對衛星的集總干擾。現有研究中針對于5G系統和GSO衛星系統之間干擾的主要緩解技術有:增大保護距離的距離保護法;選擇不同基站天線或設置基站角度保護閾值的基站天線設置保護法;增大地球站天線仰角設置保護法。

上述傳統干擾計算方法應用于5G系統對大規模NGSO衛星系統的干擾計算時,由于大規模衛星系統涉及到的時變參數眾多,鏈路特征不斷變化,導致分析大規模NGSO衛星系統與5G系統之間干擾的復雜性陡增,此外,存在難以獲得衛星覆蓋范圍內5G系統實際分布的問題。文獻[23]中提出了基于衛星空間分布概率的大規模NGSO系統間下行鏈路干擾分析方法,可減少干擾計算量,但沒有研究衛星系統上行鏈路的干擾場景。文獻[24]中針對于5G系統對于NGSO系統的干擾,利用空間地理大數據,基于聚類方法使衛星波束范圍內5G系統位置符合實際分布,但考慮到NGSO衛星波束以外的可視范圍也可能受到5G系統的干擾,存在所需空間地理位置數據量過大的問題。

基于此,本文分析了5G系統對大規模NGSO衛星系統干擾場景的特點與建模方法。針對場景特點,在對衛星星座上行鏈路建模時,依據星座衛星空間分布概率分層劃分子空域,減少衛星星座的干擾計算量。針對建模方法,在對5G系統建模時,分區域采用聚類方法或依據全球城市人口數量計算干擾的方法,減少干擾計算所需數據量。仿真結果表明,與傳統外推方法對比,本文所提方法準確度相近,但計算效率顯著提高。

1 干擾共存場景

1.1 場景介紹

5G系統對大規模NGSO衛星互聯網系統衛星的干擾場景如圖1所示。如圖1(a)所示,大規模NGSO衛星系統包含層軌道衛星與地球站,衛星采用動態點波束,5G系統包含基站和用戶,考慮NGSO衛星可視范圍內5G系統對于衛星的干擾。如圖1(b)所示,不同仰角衛星的波束足跡不同,隨著衛星相對于地面的仰角減小,波束足跡變化,與衛星相對于地面高仰角相比,衛星相對于地面低仰角時的點波束覆蓋范圍明顯增加。

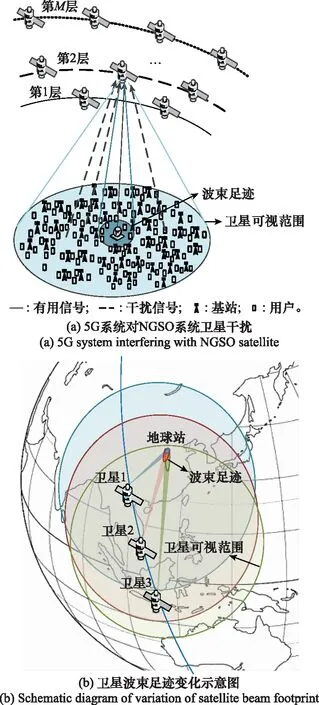
圖1 5G系統對大規模NGSO衛星系統衛星干擾場景Fig.1 Interference scenarios of the 5G system interfering with satellites in large-scale NGSO satellite system

1.2 計算量分析

當計算5G系統對NGSO衛星系統干擾時,干擾計算總次數的表達式如下:

=··

(1)

式中:為衛星系統受擾鏈路的數量;為5G系統施擾鏈路的數量;為時刻數。

由于地面5G系統用戶的位置和被激活的基站位置時刻都在變化,對于5G系統的建模,一般采用靜態蒙特卡羅仿真法生成足夠數量的快照,即用戶所處的位置和激活的基站位置是靜態隨機確定的,且在每個快照中的位置狀態是獨立的,與上一個快照中的位置狀態無關。由于NGSO衛星互聯網星座的衛星位置具有動態變化性,傳統外推方法按照一定的時間和步長將衛星通信系統的運行時間劃分為多個時間片段,在每個時刻,外推計算衛星位置和鏈路指配關系,并匹配采用靜態蒙特卡羅法隨機生成的5G系統快照。為遍歷星座全部衛星可能出現的位置,傳統外推法需要以足夠小的步長和足夠長的時間劃分時間片。例如以5 s為步長,1 d為仿真時間,式(1)中時刻數=17 280。

在每個時刻,計算5G系統對于NGSO系統衛星的干擾時,受擾鏈路的數量由地球站接入的衛星數決定,一般接入的衛星數有限。而衛星覆蓋范圍包含的5G系統基站和用戶數量往往較多,導致施擾鏈路的數量較大。

衛星覆蓋區域面積計算公式如下:

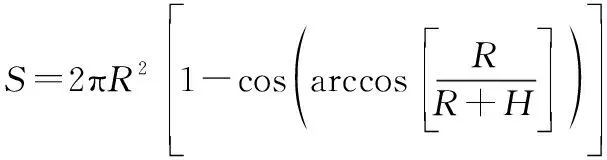
(2)

式中:是地球半徑;是衛星軌道高度。

衛星覆蓋范圍內基站數量表達式如下:

=·····

(3)

式中:是5G系統基站的部署密度;是熱點地區與建成區的比例;是建成區占總區域的比例;是網絡負載因數;為時分雙工因子。

設為基站調度用戶數目,考慮5G系統上行、下行鏈路對于衛星的干擾,則施擾鏈路的數量=·2。令=30個km,=005,=1,=02,=1,=6 378 km,=1 000 km,=3,則施擾鏈路的數量=624×10。

由上述分析可見,如采用傳統方法仿真5G系統與大規模NGSO衛星系統之間的干擾,由于和數量巨大,干擾計算量驟增,需研究合理的等效方法減少計算量。

1.3 干擾計算模型

在每個時刻,對于每個衛星系統受擾鏈路,通過將NGSO衛星系統接收到的衛星可視范圍內條5G系統施擾鏈路的集總干擾與干擾限值相比,從而確定是否會產生干擾。

第條施擾鏈路的干擾表達式如下:

=++()-()

(4)

式中：為5G系統發射端折算到NGSO衛星系統通信帶寬的發射功率；為5G系統發射端在衛星方向的天線發射增益；()為衛星系統接收端在偏離天線主軸方向的接收天線增益；()為5G系統發射端和衛星系統接收端之間距離為時對應的鏈路損耗。

式(4)中前兩項可表示為5G系統等效全向輻射功率(effective isotropic radiated power, EIRP)+=EIRP。除了與5G系統發射功率、天線參數等相關外,EIRP還與衛星相對于5G系統的方向有關。由于難以獲得衛星覆蓋范圍內5G系統的實際位置分布,需要采取等效的方法確定5G系統位置。由于施擾鏈路數量較大,考慮系統內部調度時計算量巨大,需采取等效的方法減少輻射能量EIRP的計算量。

式(4)中第3項()與衛星位置和衛星指向有關,考慮到大規模星座一般采用動態點波束,假設衛星指向隨機,則()主要與衛星位置有關。式(4)中第4項可參照ITU建議書中的模型。

綜上所述,干擾可表示為上述主要影響因素的函數,表達式如下:

=(,,,EIRP,)

(5)

2 方法

在上述影響干擾的主要影響因素分析基礎上,本文的等效建模方法主要分為3個部分:

(1) 對衛星星座建模時,利用依據星座衛星出現概率劃分子空域的方法,等效衛星位置、簡化時刻數計算;

(2) 在對5G系統建模時,對于在衛星3 dB波束范圍內的5G系統采用聚類方法和基于EIRP相等的輻射能量確定方法,等效5G系統位置、簡化輻射能量EIRP、施擾鏈路數計算;

(3) 在對5G系統建模時,對于在衛星可視區域范圍內、衛星3 dB波束范圍外的5G系統采用依據全球城市人口數量計算干擾的方法,等效5G系統位置、簡化施擾鏈路數計算。

2.1 星座子空域劃分

由于利用傳統外推的方法,在計算大規模星座干擾時,需要外推成千上萬顆衛星的位置,導致計算量較大。針對于大規模星座,文獻[23]中,劃分地球站可視空域為多個子空域,在每個子空域內放置一顆衛星,將動態變化衛星位置轉化為靜態衛星位置,從而減少計算量,所提方法與外推法對比,兩個NGSO星座的下行鏈路間干擾概率分布存在約15%的誤差。

根據文獻[23],對于單層星座,地球站可視空域內衛星的出現概率計算公式為:當星座衛星總數為,對某一確定地球站,其方形或圓形子空域內,星座內任意一顆衛星的出現概率為

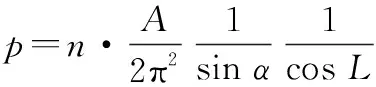
(6)

式中:為子空域的球面積;為衛星軌跡與子空域中心緯度線的夾角;為計算子空域中心的緯度,其計算公式分別為

=Δ·Δ(rectangle)

(7)

(8)

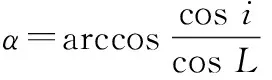
(9)

=arcsin(cos·sin+sin·cos·cos)

(10)

式中:Δ、Δ分別為子空域的俯仰角差、方位角差對應的地心角差;為衛星軌道的傾角;為地球站的緯度;為子空域中心相對地球站的方位角;為子空域中心與地球站的地心角。

根據如下3個準則劃分子空域:

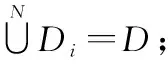
(2)∩=?,≠;

(3),≈1,且一個子空域有超過一個衛星的概率約等于0。

如圖2所示,為地心角維度下,以方形劃分為例,地球站可視空域劃分子空域示意圖。

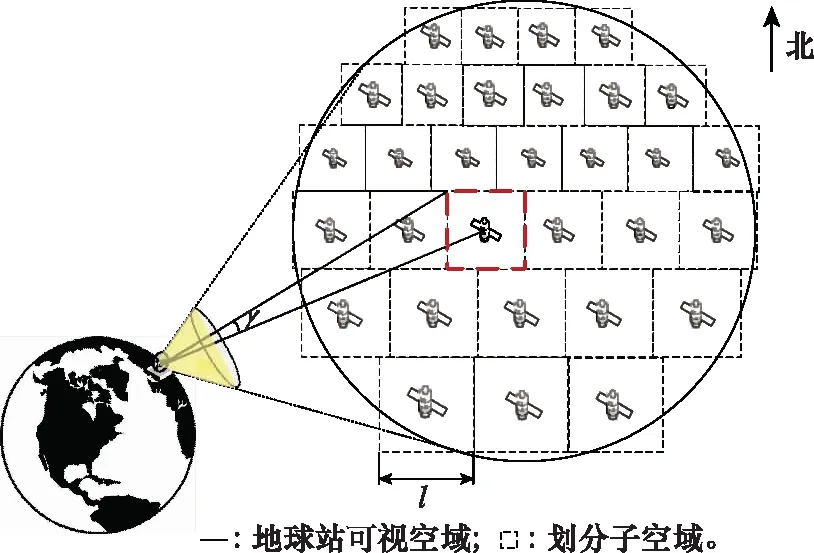
圖2 地球站可視空域劃分子空域示意圖[23]Fig.2 Schematic diagram of the sub-airspace of the visible airspace of the Earth station[23]

考慮到衛星天線的非線性,若衛星數量較大,則劃分的子空域面積足夠小,即衛星在子空域中心或邊緣出現時相對于地球站的地心角足夠小,衛星在子空域中的位置對地球站干擾接收值計算的影響很小,可在子空域中放置一顆虛擬衛星,利用虛擬衛星等效為子空域中任意位置衛星。為方便計算,可將衛星放置在子空域中心。本文干擾共存場景中,對于衛星系統上行鏈路,基于大規模NGSO衛星星座衛星數量龐大的特點,利用劃分子空域的方法確定地球站接入衛星的位置。如圖3所示,衛星被5G系統基站/用戶干擾。衛星作為受擾方,根據軌道高度,將星座分為多層子星座。

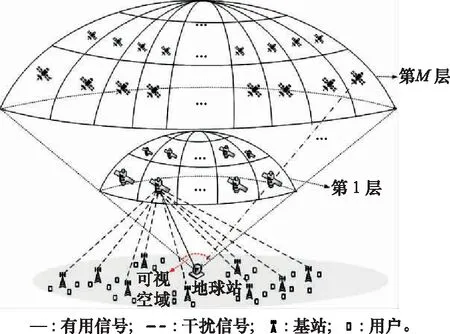
圖3 地球站可視空域劃分為多層子星座Fig.3 Schematic diagram of the visible airspace of the Earth station divided into multiple sub-constellations

對于各層子星座,分別在以地球站為球心的可視空域內,根據衛星星座的衛星出現概率劃分子空域,子空域中心放置一顆虛擬衛星,從而得到各層的虛擬衛星位置分布。基于虛擬衛星位置分布,利用地球站接入策略得到地球站接入的衛星位置。

通過上述方法將動態變化的衛星靜態化,只需計算一種衛星位置分布與足夠數量5G系統快照之間的干擾,使干擾計算中時刻數與衛星位置變化無關,只需考慮5G系統的變化,從而減少干擾計算量。

2.2 采用聚類方法和基于EIRP相等的輻射能量確定方法計算5G系統干擾

傳統方法對衛星波束范圍內的5G系統建模時,通常將全部5G系統等效為多個局部區域5G系統,局部區域位置在波束覆蓋范圍內均布或隨機分布。由于受限于地形、地貌等因素,不同城市區域的建設情況不同,傳統方法會導致5G系統熱點區域分布不符合城市發展現狀。針對上述問題,文獻[24]中,依據城市建筑大數據,采用聚類方法,使5G系統位置符合實際分布,基于EIRP相等,通過累積分布函數(cumulative distribution function,CDF)曲線擬合確定5G系統輻射能量EIRP,減少了5G系統干擾計算量,并通過仿真驗證了所提方法的可行性。考慮到衛星覆蓋范圍內建筑數據量較大,因此僅對衛星3 dB波束范圍內5G系統干擾采用聚類方法和基于EIRP相等的輻射能量確定方法,如圖4所示。

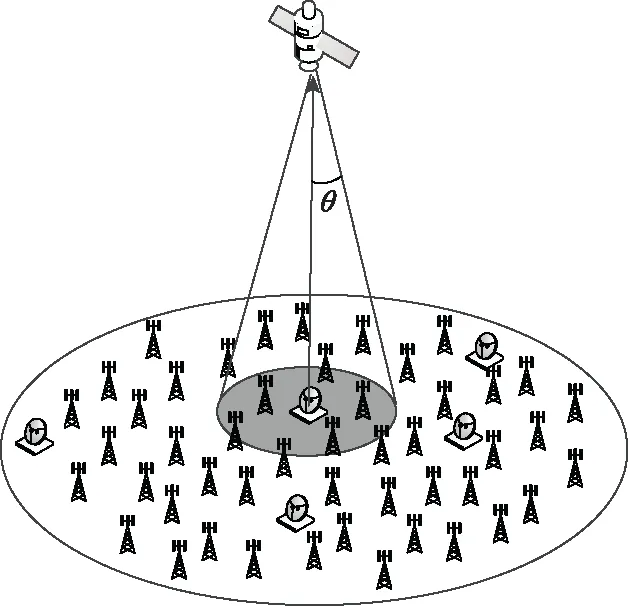
圖4 衛星3 dB波束范圍內5G系統干擾Fig.4 5G system interference inside the 3 dB beam range of the satellite

2.2.1 聚類方法

設衛星3 dB波束范圍內共有個城市,每個城市5G系統的干擾等效為多個等效大基站的干擾。令一個等效大基站對應的城市面積為,根據第個城市的城市面積確定城市的等效大基站個數,表達式如下:

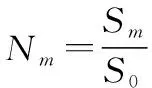
(11)

依據城市興趣點(point of interest, POI)大數據給出的建筑的經緯度地理坐標={,,…,|=(Lon,Lat),=1,2,…,},采用聚類的方法,得到城市商業建筑的個聚類簇=,1∪,2∪…∪,,聚類簇中心作為等效大基站的位置,即5G系統位置。

根據式(3)可由城市面積計算城市基站總數BS,和用戶總數UE,。依據各聚類簇中建筑物的數量|,|占城市總建筑數||的比例,第個等效大基站包含的5G系統基站數量BS,,和用戶數量UE,,的表達式如下:

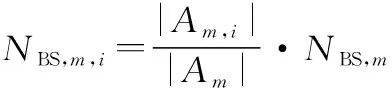
(12)

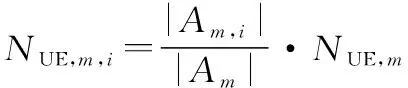
(13)

222 基于EIRP相等的輻射能量確定方法

一般情況下,用戶和基站之間的相對方位隨機,5G系統在各方位角的輻射能量較均勻。由于用戶一般低于基站的高度,基站和用戶在各個仰角上的輻射能量不同。因此,可利用局部區域的基站和用戶調度,擬合基站和用戶在不同仰角EIRP的CDF曲線。利用衛星相對于等效大基站的仰角,選擇對應的CDF曲線,在區間[0,1]選取均勻分布隨機數作為CDF曲線的縱坐標概率值,通過CDF曲線得到基站和用戶的隨機EIRP值。通過EIRP相等的方式,將第個聚類簇中的全部基站和用戶等效為第個大基站,表達式如下:

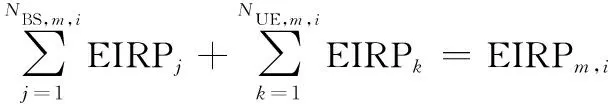
(14)

等效大基站對衛星的干擾為IMT,,,衛星3 dB波束范圍內的等效大基站對于衛星的集總干擾可通過如下公式得到:

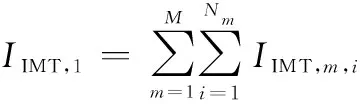
(15)

通過等效大基站代替聚類簇中包含的基站和用戶,可減少計算量。例如,一個面積為6 000 km的城市,令基站的部署密度=30個km,=005,=1,=02,=1,根據式(3),城市中基站總數為1 800個,若每200 km設置一個等效大基站,則共有30個等效大基站,計算的干擾基站數減少了60倍。

2.3 依據全球城市人口數量計算5G系統干擾

由于衛星可視范圍很廣,常包含多個國家,采用第2.2節方法時需要獲取與處理的數據量過大,因此方法2不適用于如圖5所示的衛星波束外大范圍5G系統建模。針對大范圍的5G系統建模,文獻[16]中基于城市人口數據,在城市中心設置局部5G系統,等效計算城市中所有5G系統干擾,可減少計算量并使5G系統分布模型符合城市分布。考慮到波束范圍外的5G系統干擾一般較小,同一個城市中不同位置5G系統的干擾相近,因此可采用文獻[16]中的方法,以城市為單位計算5G系統的干擾。

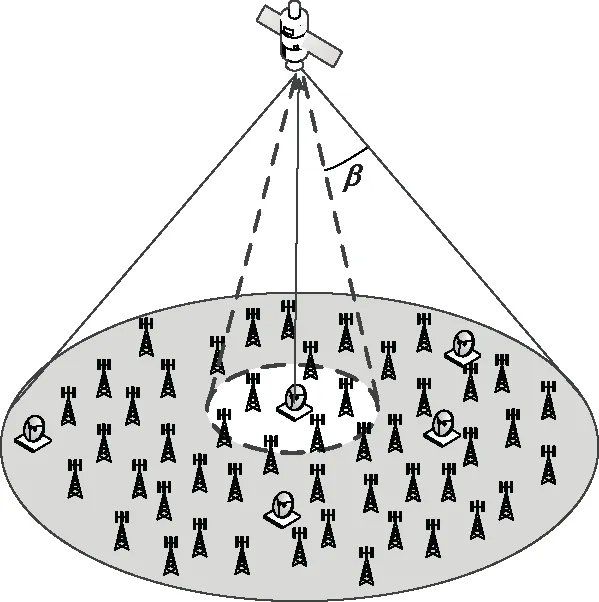
圖5 衛星3 dB波束范圍外5G系統干擾Fig.5 5G system interference outside the 3 dB beam range of the satellite

通過從全球選出部分典型城市的方法,確定每個基站對應的平均人口數量。設共有個典型城市,個典型城市的基站總數可通過式(3)得到。根據第個城市的人口數,每個基站的平均人口數可通過下式得到:

(16)

通過在城市中心設置干擾單元的方式,等效城市范圍內的5G系統的干擾,以城市中心的部分5G系統為一個干擾單元,第個城市包含的干擾單元數1,可通過下式得到:

(17)

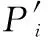
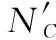
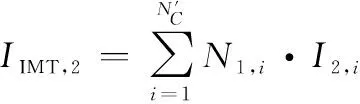
(18)

經過前文計算,一個面積為6 000 km的城市,包含1 800個基站,若城市中心干擾單元包含的基站數為6個,則通過等效的方法,計算的干擾基站數減少了300倍。

在實際仿真時,設全球人口數為,若用于計算的城市人口總數小于,可將每個基站的平均人口數乘以一個比例因子,從而等效全球人口,比例因子表達式如下:

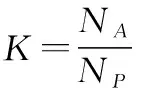
(19)

3 仿真分析

考慮到第22節方法與第23節方法均已在文獻中驗證過可行性,空間段采用Starlink的首期LEO星座,對比第2.1節方法與實際外推的效果。如表 1所示,為Starlink子星座的星座構型。本文方法適用于大規模星座,且子星座衛星數越多,結果越準確。由于Walker星座的主要特性為軌道平面和軌道平面內衛星分布均勻,星座構型與升交點赤經、相位等因素相關性較小,主要與軌道的傾角和高度有關。根據軌道傾角和軌道高度,分別取前2個子星座和后3個子星座的軌道高度、傾角平均值,劃分為兩個子星座“LEO1”“LEO2”。劃分后星座的軌道構型如表2所示。

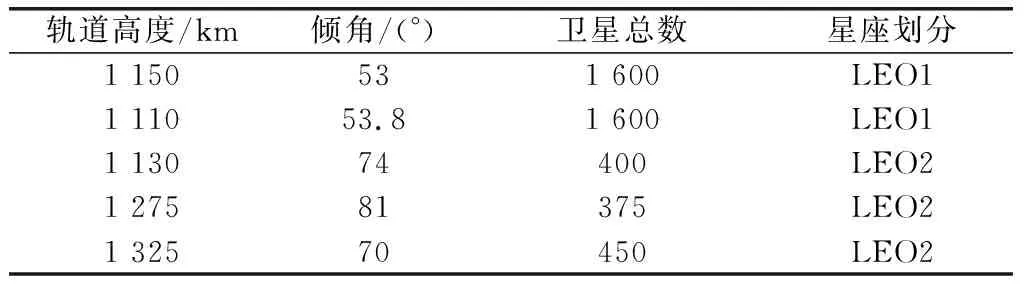
表1 Starlink衛星系統LEO星座構型

表2 Starlink系統子星座軌道構型

根據式(4),干擾值主要和仰角以及鏈路傳播距離有關,根據自由空間傳播模型,簡化后的軌道高度偏差對于干擾的影響不大(最多為0.87 dB)。此外,星座構型簡化只是為了對比概率法和外推法,也可以不簡化,用原星座計算。在赤道上空設置均勻分布的360顆地球同步軌道衛星,相鄰同步衛星的軌位間隔均為1°。仿真中Starlink系統采用空域隔離的方法規避對GSO衛星的干擾,設置15°的隔離角。

考慮Stailink系統和地面5G系統在實際應用中的潛在重疊頻段,根據引言中的同頻分析,選取28.35 GHz作為系統間干擾仿真的中心頻率。為了使參數設置符合實際,衛星系統參數參考ITU登記的衛星數據庫STEAM-2,選取仿真頻率對應的衛星天線和地球站參數。5G系統參數選取ITU第五研究組建議書中,仿真頻率所對應的5G系統參數；地面段分布有5G系統和地球站。設置地球站位于太原市中心,地球站根據采用最高仰角法接入策略,選擇5顆衛星接入,衛星波束中心指向地球站,仿真衛星受到5G系統的干擾。5G系統內部的傳播模型參考第3代合作伙伴計劃(3rd generation partnership project,3GPP)組織TR 38.900《6 GHz以上信道模型研究》文檔中的視距傳播模型。衛星和5G系統之間的傳播模型參考ITU-R P.619建議書、ITU-R P.2108建議書。考慮5G系統工作在時分雙工(time division dual,TDD)模式,基站/終端在相同的頻段進行信號的收發操作。仿真采用Matlab軟件,仿真PC機的處理器性能為:Intel(R) Core(TM) i7-6700 CPU @ 3.4 GHz,3401 Mhz,4個內核,8個邏輯處理器。干擾共存場景的仿真參數設置如表3所示。

表3 5G系統對Starlink系統上行鏈路干擾仿真參數

續表3

以傳統實際外推衛星位置的方法(外推法)得到衛星位置,仿真時間為1 d,仿真步長為5 s,采用蒙特卡羅仿真法,每個時刻基站位置、用戶位置不同,用以模擬5G系統分布的隨機性。仿真衛星波束3 dB內、外的5G系統對Starlink星座上行鏈路干擾,如圖6所示。由仿真結果可以看出,考慮衛星波束3 dB外的5G系統干擾后,衛星可視范圍內的5G系統干擾增加。因此,有必要依據全球城市人口數量計算衛星波束3 dB外5G系統干擾。

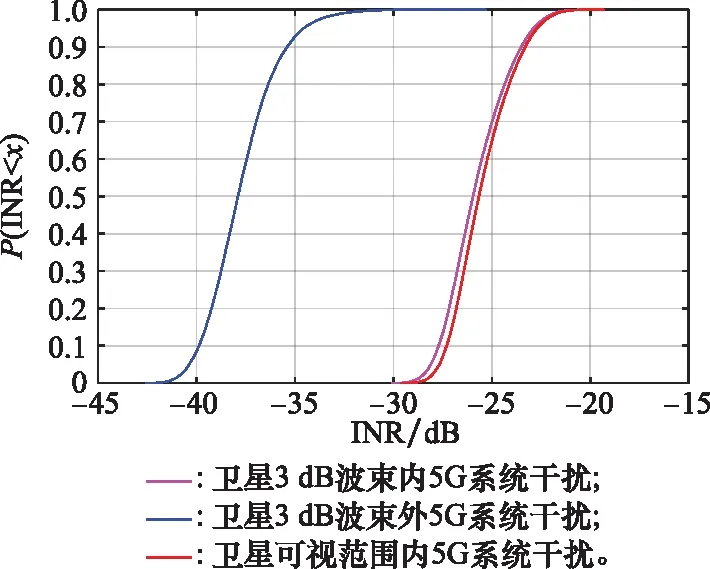
圖6 衛星波束3 dB內、外5G系統干擾對比Fig.6 Comparison of interference from 5G systems inside and outside 3 dB of satellite beam

利用第2.1節方法,依據星座衛星出現概率在兩個子星座中分別劃分子空域,通過在子空域中心位置放置虛擬衛星的方式分別得到兩個子星座的衛星位置分布。

利用第2.2節方法,采用聚類的方法計算衛星3 dB波束范圍以內5G系統干擾。通過獲取以太原市為中心的9個城市的POI數據,依據城市所有商業建筑的經緯度地理坐標,將城市商業建筑劃分為224個聚類簇。利用9個城市的城市面積,計算城市的基站總數,由每個聚類簇中包含的建筑數所占總建筑數比例,得到每個聚類簇對應的基站數和用戶數。

按照表 3中所給5G系統參數,仿真2 km局部區域的基站和用戶調度,以1°為間隔,得到基站和用戶在0°到90°仰角上的EIRP值,并擬合CDF曲線。如圖7、圖8所示,為基站和用戶在部分仰角方向EIRP的CDF擬合曲線。

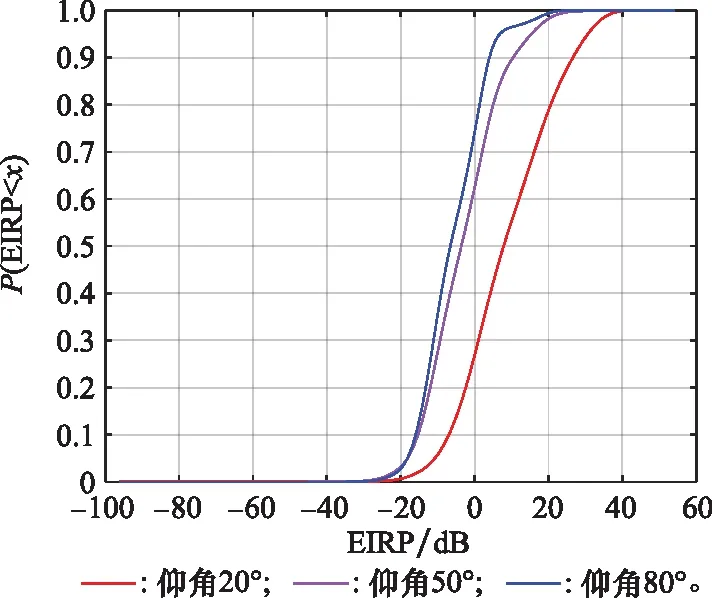
圖7 基站在不同仰角方向EIRP的CDF擬合曲線Fig.7 CDF fitting curves of the EIRP of the base station at different elevation angles

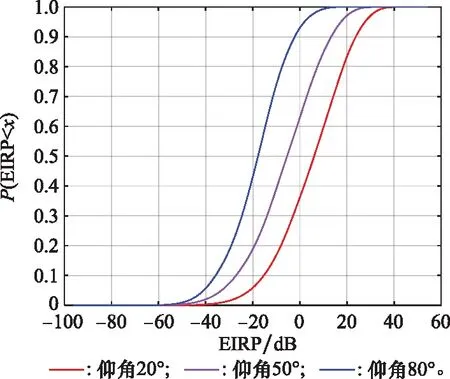
圖8 用戶在不同仰角方向EIRP的CDF擬合曲線Fig.8 User’s CDF fitting curves of EIRP at different elevation angles

在擬合的CDF曲線上隨機讀取基站和用戶的EIRP值,得到聚類簇對應的等效大基站的EIRP值。所有等效大基站對衛星的集總干擾為衛星波束范圍內5G系統干擾。

利用第2.3節方法,依據全球城市人口數量計算衛星3 dB波束范圍以外5G系統干擾。根據ITU研究中的統計數據,室外場景下每個基站的平均人口數為1 924。采用來源于“www.geonames.org”的“cities15 000”數據庫。利用人口數超過50萬人的807個城市,人口總計13億。每個城市中心的5G系統干擾單元面積為1 km,包含30個基站,在計算總體干擾時,每個城市的干擾根據干擾單元的干擾以及城市人口、比例因子縮放。

5G系統對衛星的集總干擾為衛星3 dB波束范圍內、外5G系統干擾之和。仿真2 000個5G系統快照,用以模擬5G系統分布的隨機性。采用本文所述方法與外推法仿真5G系統對Starlink系統衛星的干擾情況,干噪比累積分布曲線如圖9所示。

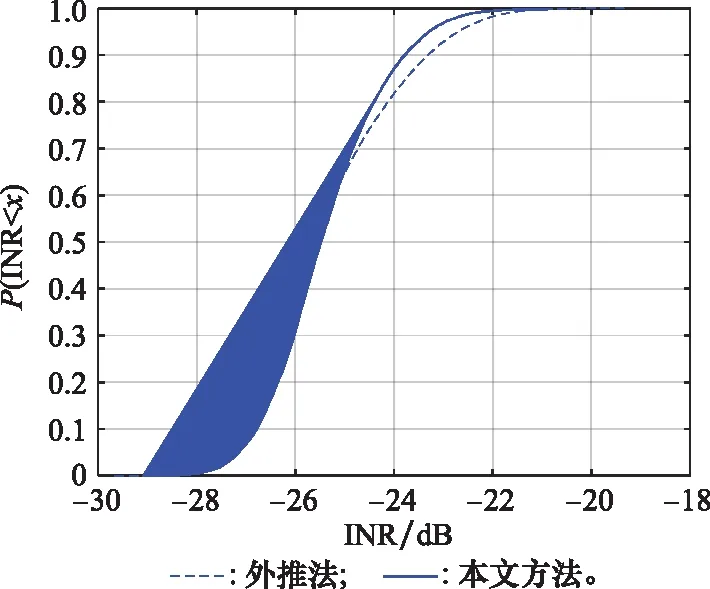
圖9 5G系統對Starlink系統衛星I/N累積分布曲線Fig.9 I/N cumulative distribution curve from 5G system to Starlink system satellite

干擾結果統計如表4所示。

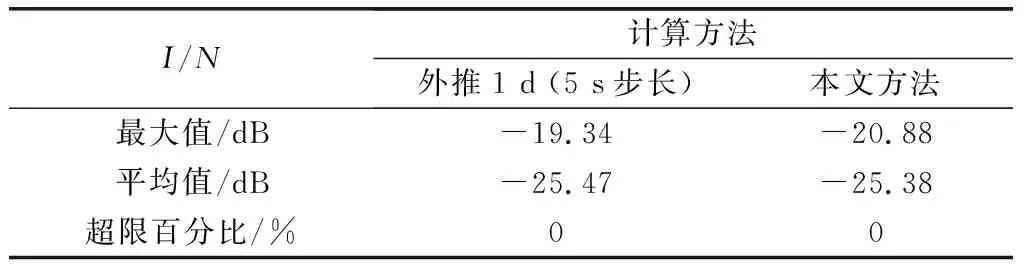
表4 5G系統對于Starlink衛星的干擾結果統計

仿真時間如表 5所示。

表5 外推法與本文方法仿真時長對比

根據仿真結果,本文方法與外推法相比,減少了仿真的時長,累積分布曲線趨勢相同,干擾概率分布曲線存在較小的誤差,最大值相差1.54 dB,平均值相差0.09 dB。仿真的誤差是對動態變化的衛星靜態化造成的,隨著NGSO星座規模的擴大,本文方法劃分的子空域面積減小,用靜態衛星替代動態衛星的誤差可減少。例如NGSO星座采用如表6所示的A星座構型,其余仿真參數相同,對比本文方法與外推法的仿真結果。

表6 A星座構型

累積分布曲線如圖10所示。

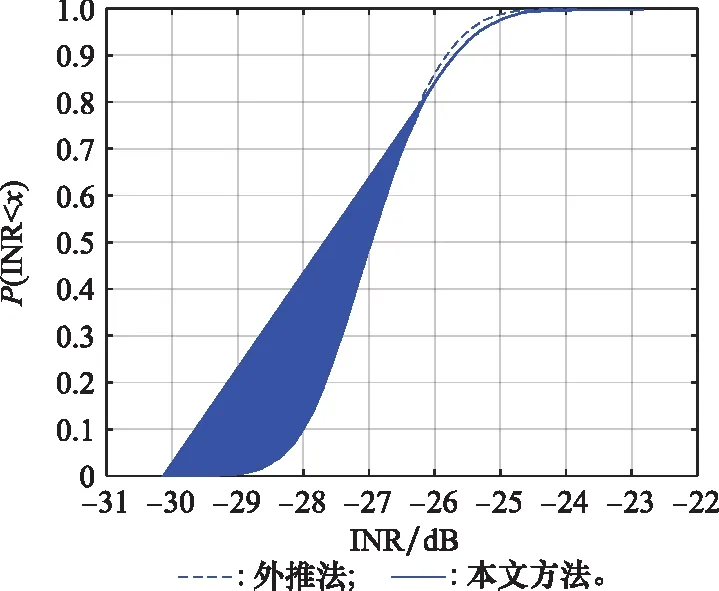
圖10 5G系統對A星座衛星I/N累積分布曲線Fig.10 I/N cumulative distribution curve from 5G system to A constellation satellite

干擾結果統計如表7所示。

表7 5G系統對于A星座衛星的干擾結果統計

根據仿真結果,本文方法與外推法相比,最大值相差0.98 dB,平均值相差0.06 dB,誤差減少。

將本文仿真結果與現有文獻[32]的仿真結果對比,文獻[32]中通過SHARC軟件仿真,仿真參數的主要區別如表8所示。

表8 文獻[32]仿真參數

文獻[32]仿真結果如圖11所示。

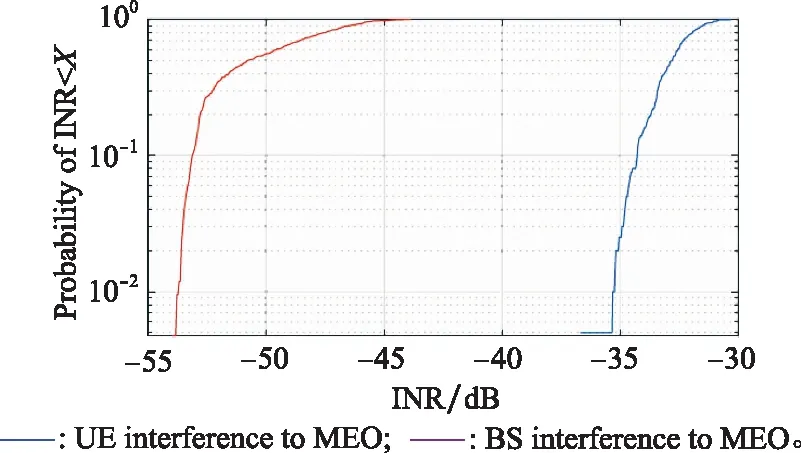
圖11 文獻[32]I/N累積分布曲線Fig.11 I/N cumulative distribution curve in literature [32]

根據自由空間傳播模型:

=925+20lg+20lg

(20)

式中:為干擾信號的載波頻率(GHz);為干擾信號的傳播距離(km)。

本文星地鏈路損耗與文獻[32]中星地鏈路損耗′相差為Δ=-′=-1607 dB。因此,根據式(4),干擾值相差為Δ=Δ+Δ+Δ+Δ=1487 dB。經計算,系統噪聲相差為-3 dB,則干噪比理論相差為11.87 dB。因此,如仿真結果所示,本文5G系統對衛星的最大干噪比(約為-20 dB)比文獻[32]中最大干噪比(約為-31 dB)嚴重約11 dB。

本文方法可用于仿真干擾緩解技術的效果。采用改變基站天線陣元的干擾緩解技術,仿真5G系統對Starlink系統衛星的干擾情況,累積分布曲線如圖12所示。

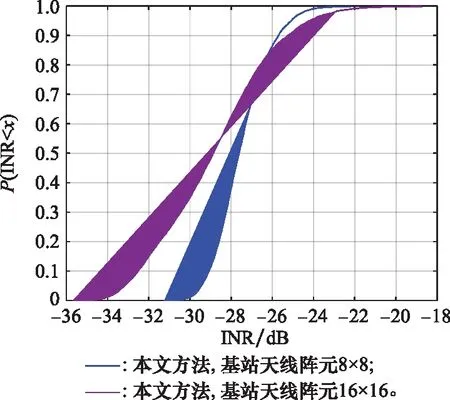
圖12 采用干擾緩解技術后的I/N累積分布曲線Fig.12 I/N cumulative distribution curve after adopting interference mitigation technology

根據仿真結果,當基站天線陣元為16×16時,最大值大于基站天線陣元為8×8的情況,但干噪比平均值小于基站天線陣元為8×8的情況。由此可見,改變基站天線陣元的干擾緩解方法可減小平均干擾。干擾結果統計如表9所示。

表9 采用干擾緩解技術后的干擾結果統計

4 結 論

在地面5G系統和大規模NGSO衛星互聯網系統的同頻共存場景中,針對5G系統分布不符合實際以及干擾計算量較大的問題,本文分析了大規模NGSO衛星系統與5G系統干擾共存場景的特點與建模方法。在對衛星星座建模時,利用依據星座衛星出現概率劃分子空域的方法,減少由衛星星座動態性引起的干擾計算量,在對5G系統建模時,依據聚類方法以及全球城市人口數量,使5G系統熱點區域分布在城市商業中心附近,符合城市發展現狀,并基于EIRP相等的輻射能量確定方法減少5G系統干擾計算量。在此基礎上,仿真了5G系統對于衛星星座的干擾,與傳統外推方法對比,本文所提方法能夠減少仿真的時長,由于使用了劃分子空域近似巨型星座的方法,引入了一定的誤差,但誤差范圍很小。將本文所提方法與現有文獻仿真結果對比,結果相符。因此,本方法可用于計算地面5G系統和大規模NGSO衛星互聯網系統之間的干擾以及驗證干擾規避策略的效果。