基于Agent的體系過程A-GERT網絡“刺激-反應”學習模型

方志耕, 夏悅馨,*, 張靖如, 熊 儀, 陳靜邑

(1. 南京航空航天大學經濟與管理學院, 江蘇 南京 211100;2. 南京航空航天大學灰色系統研究所, 江蘇 南京 211100)

0 引 言

圖示評審技術(graphic evaluation and review technique, GERT)[1]是由Elmaghraby和Pritsker提出的一種概率型隨機網絡,近年來,GERT在項目進度規劃[2]、災害應急預警[3]、供應鏈優化流程[4]、衛星網絡[5]等領域得到廣泛的應用。GERT網絡可以通過概率分支決定下一節點的狀態,網絡節點具有決策功能,能夠很好地研究具有決策過程的現實問題。陳東平等[6]將GERT網絡應用于工程計劃管理中,通過模擬解模型過程的分析從而尋找GERT網絡解,決策出關鍵線路。楊保華等[7]基于GERT網絡構建突發事件情景推演耦合模型,為“情景-應對”決策研究提供了新思路。郭本海等[8-10]通過對GERT網絡模型節點決策概率的研究,分析了產業價值流動、資源優化配置等問題。張海濤等[11]構建了網絡信息價值流動的GERT網絡模型,通過分析網絡模型的傳遞參數描述信息生態鏈中各信息主體之間的價值流動過程。通過以上研究不難看出,GERT網絡在解決網絡流程分析、邏輯決策等方面發揮了重要的作用。但GERT網絡在應用決策過程中通常都設定節點傳遞概率是靜態不變的,而在實際決策過程中,傳遞概率的大小很大程度上決定了鏈路的優劣,在不確定環境以及不同系統目標的影響下,網絡傳遞概率會發生動態變化,決策結果也會相應改變。

另一方面,隨著人工智能技術的不斷發展,基于智能體(Agent)的學習決策[12-14]已成為決策問題研究的熱點之一。關于Agent的定義,Wooldrige等[15]認為Agent不僅具有自適應性、社會性、反應性和能動性,還具備一些人類才有的信念、意圖等性質。基于Agent的決策系統具有很好的學習能動性和環境自適應性,因此將Agent應用于GERT網絡中研究決策問題可以形成良好的互補關系。研究Agent的GERT網絡決策問題主要包含兩個方面:一是決策節點能夠無阻礙有效識別路徑,即減少回路的概率流動,最大程度地規劃有效路徑；二是根據不同的目標要求,實現最優路徑的概率最大化。目前雖然已有蔣子涵等[16]將GERT網絡和Agent技術結合起來,但主要關注的是Agent學習算法的一致性分析,較少從GERT網絡模型的角度研究路徑概率學習決策問題。

以上兩個決策問題本質上即是決策節點的反饋學習問題,在研究Agent的學習問題中,迭代學習的概念[17]自Uchiyama首次提出后便引起了廣泛關注,由于迭代學習具有能夠從以前迭代的經驗中進行學習的優點,可以有效地實現對Agent系統的精確跟蹤。在早期的迭代學習研究[18-19]中,學習算法通過增加固定的效益來進行迭代,但削弱了不確定性所帶來的影響。之后,Chi等[20]和Lin等[21]引入了自適應控制的思想,提出了一種自適應迭代學習方法。Chen等[22-23]針對非線性系統提出了模糊自適應迭代學習方法。但在自適應迭代學習過程分析中仍需要一些先驗模型信息,如線性參數和系統狀態等。而隨著系統網絡結構的復雜化,模型過強的非線性也導致學習分析十分困難。針對迭代學習存在的自適應性以及非線性問題,約翰霍蘭教授提出的復雜適應系統(complex adaptive system, CAS)[24]理論中最為核心的概念就是適應性主體,簡稱主體。主體與外部環境之間能動的不斷學習的交互作用所體現的就是適應性。刺激-反應模型[25-27]作為CAS理論中的基本模型在自適應學習以及決策領域得到了廣泛應用,主體通過外界刺激反饋驅動系統做出反應,僅利用輸入輸出實現對復雜系統的迭代學習,對于研究非線性系統有較強的適應性。

綜上所述,就GERT網絡決策以及Agent學習研究而言,存在的局限性主要有以下3個方面:① 多數GERT網絡研究主要針對活動過程的描述分析,傳遞概率通常都是靜態不變的,未考慮網絡節點本身因環境影響所帶來的傳遞概率的變化,決策節點不具備學習能動性。② 在Agent技術與GERT網絡結合的研究中,大多針對學習算法本身的分析研究,很少從網絡決策節點的角度去探討概率的路徑優化學習。③ 在Agent迭代學習方面,系統的環境自適應性與模型過強的非線性問題導致迭代學習十分困難。

因此,本文針對以上局限性,首先將Agent技術與GERT網絡節點結合起來,形成智能決策節點;然后在A-GERT網絡的基礎上結合刺激-反應模型,通過網絡節點的傳遞效用值進一步拓展刺激-反應模型,建立迭代學習反饋機制,并運用動態規劃原理依次對網絡節點進行概率學習;最后給出了基于Agent的A-GERT網絡“刺激-反應”模型的設計步驟,并以創新技術開發活動資源配置決策問題為例,驗證本模型的有效性和合理性。

1 基于Agent的體系過程GERT網絡邏輯及其結構設計

系統是由相互關聯的要素構成的整體。而體系則是由系統所構成的一個協同(聯盟)整體,因為體系中的系統可能具有較強的獨立性,甚至有時,某(幾個)系統可以部分(完全)地代表它的總體。因此,體系與系統的一個重要區別在于,體系一般都具有一定的可靠性結構和量值韌性,而系統一般卻很難具有這樣的性質。

定義 1體系過程Ψ(t):若某體系是一種由若干系統Si(i=1,2,…,n)組成,且協同完成某種(些)任務的隨機(網絡)過程,則稱其為體系任務網絡隨機過程,簡稱隨機過程,用Ψ(t)表示。

定義 2自學習體系過程ΨAgent(t):在Ψ(t)過程中,若把某個(些)系統(組織)看作Agent,具有向過程或歷史學習的機制和能力,則稱該體系為具有Agent自學習機制的過程,其本質是一種由若干智能代理人Agent構成的協作過程,用ΨAgent(t)表示。

定義 3體系自學習網絡ΨAgent(N(t),S(t)):若將ΨAgent(t)過程用廣義活動網絡(generalized active network, GAN)[28]的邏輯機制進行表征,則稱所得到的網絡為具有Agent自學習機制的體系過程網絡,用ΨAgent(N(t),S(t))表示,其中:N(t)和S(t)分別表示某系統具有自學習機制的網絡節點和邊。

根據隨機網絡原理,對于任一客觀體系過程,可以看作是基于任務目標的各系統之間相互協作過程,一般情況下,這種任務的協作過程可以運用GAN進行表征,邏輯節點構成見圖1。這里值得注意的是,N(t)和S(t)分別表示各系統(組織)經過學習,其狀態和過程可能都會逐步改善或得到完善,其(t)表示是一個時間的映射。為了便于區別,在其邏輯節點上加注點(見圖1、圖2)。

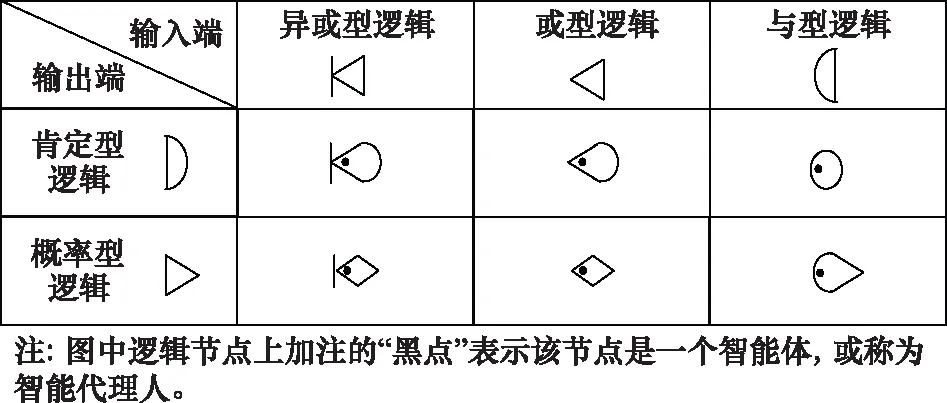
圖1 GAN網絡節點類型Fig.1 Type of GAN network node

圖2 ΨAgent(N(t),S(t))網絡的要素Fig.2 Elements of ΨAgent(N(t),S(t)) networks

定義 4ΨAgent(N(t),S(t))網絡:在ΨAgent(N(t),S(t))網絡中,若依據邏輯轉換規則,將其所有節點都轉換成異或型,則稱該網絡為具有自學習機制的A-GERT,為簡便,該網絡用ΨA-GERT(N(t),S(t))表示。

例 1某體系中,節點i保持其在原狀態的概率為pii,到后續節點jk(k=1,2,…,K)的概率分別為pij1,pij2,…,pijK,試畫出該節點與其后續節點的ΨA-GERT(N(t),S(t))圖。

利用上述各定義中的A-GERT網絡邏輯畫出其ΨA-GERT(N(t),S(t))網絡圖,如圖3所示。

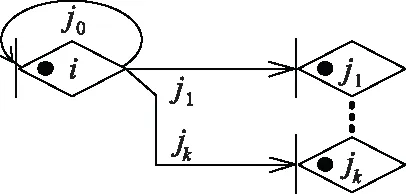
圖3 某體系節點i到jk(k=1,2,…,K)的ΨA-GERT(N(t),S(t)) 網絡示意圖Fig.3 Schematic diagram of the ΨA-GERT(N(t),S(t)) network of system nodes i to jk(k=1,2,…,K)

A-GERT網絡與常規的GERT網絡的區別主要體現在決策節點的學習能動性,節點在外界環境刺激下可以動態地調整傳遞概率,從而改善體系活動過程。

定義 5[28]ΨA-GERT(N(t),S(t))網絡的解析算法:假設隨機變量tijK為活動ijK的完成時間,要知道活動ijK的執行情況,就要知道活動ijK被執行的概率以及tijK的概率分布或概率密度函數。

令f(tijK)為活動ijK的條件概率密度函數,P(tijK)為活動ijK的條件概率分布函數,則隨機變量的矩母函數為

(1)

定義WijK(s)為活動ijK的傳遞函數,則WijK(s)=pjk·Mijk(s)。如圖4所示,ΨA-GERT(N(t),S(t))網絡主要包含串聯結構、并聯結構以及自環結構。

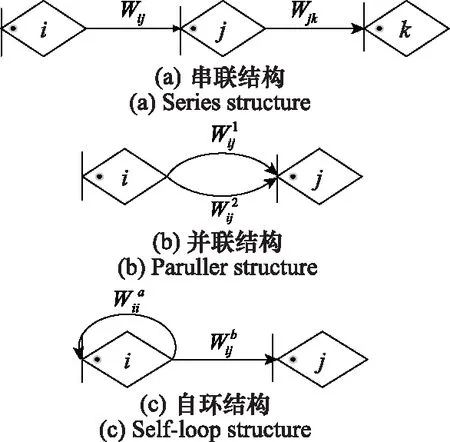
圖4 ΨA-GERT(N(t),S(t))網絡串聯、并聯、自環結構圖Fig.4 ΨA-GERT(N(t),S(t)) network in series, parallel and self-loop structure diagram

(1) 對于串聯結構,節點i與k之間等效傳遞函數為

Wik=Wij+Wjk=Mij(s)pij+Mjk(s)pjk

(2)

(2) 對于并聯結構,節點i與j之間等效傳遞函數為

(3)

(3) 對于自環結構,節點i與j之間等效傳遞函數為

(4)

定理 1設WEijk(s)(k=1,2,…,K)為節點i到節點jk的直達路徑的等價傳遞函數,節點i到節點jk的等價傳遞概率pEijk等于s=0時的WEijk(s)的值。節點i到節點jk的傳遞隨機變量tijk的期望時間TEijk等于矩母函數MEijk(s)的一階導數在s=0時的值。

證明兩節點的等價傳遞函數WEijk(s)=MEijk(s)·pEijk,由ΨA-GERT(N(t),S(t))網絡矩母函數的特性可知,在s=0時,

(5)

因此,等價傳遞概率pEijk等于s=0時的WEijk(s)的值。

根據矩母函數的基本性質,即矩母函數的一階導數在s=0處的數值,就是網絡傳遞的隨機變量的一階原點矩,因此有

(6)

證畢

2 體系過程的“刺激-反應”學習反饋結構及其機制分析

如今隨著系統網絡結構的日益復雜化,體系過程學習模型的建立和分析也更加困難,系統的自適應學習已成為研究的重點之一。而CAS理論中最為核心的概念就是適應性主體,簡稱主體。刺激-反應模型[25-27]是CAS理論中的基本模型,模型主體僅利用輸入輸出實現對復雜系統的迭代學習,具有較強的適應性。因此,本文通過對刺激-反應模型的分析研究,并結合A-GERT網絡進一步拓展刺激-反應模型。

定義 6刺激-反應模型[25]:刺激-反應模型主要由一個主體(探測器)、If/Then規則集合和一個主體行為(效應器)組成,系統所處環境刺激主體,主體從刺激信號中抽取信息,信息通過規則集反復處理,尋找最優匹配,根據If/Then規則集合判斷,傳達到效應器,由效應器做出反應,即主體行為,見圖5。

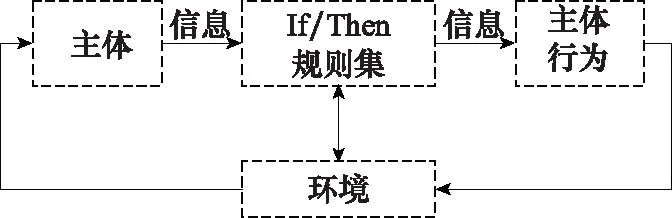
圖5 刺激-反應模型Fig.5 Stimulus-response model

定義 7網絡節點i的傳遞效用函數:在ΨA-GERT(N(t),S(t))網絡中,決策節點集合N(t)中某節點i在決策行動后,從節點i到jk的活動均經歷相應參數,即某條道路(i,jk)選擇所導致成功或者失敗的節點jk效用值Vjk、路徑(i,jk)實現期望概率pEijk、路徑(i,jk)所消耗的期望時間TEijk,該節點i行動的傳遞效用值函數Fi可以定義為

(7)

其中,終節點效用值指標Vjk可直接給出,例如活動經濟效益、活動效能等。由式(7)可知,節點i行動的傳遞效用值函數Fi與TEijk成反比,與pEijk和Vjk成正比。此外,需注意的是在計算Fi時,節點jk不包含回路節點,因為回路節點jk的效用值Vjk可認為是0。

定義 8ΨAF-GERT(N(t),S(t))智能反饋網絡:在ΨA-GERT(N(t),S(t))網絡中,各決策節點i均能對其決策后果的效用值函數Fi值進行觀察、評價,并能利用這一結果效用值Fi來改善其下一步的決策,則稱該網絡為具有反饋機制的智能網絡,記為ΨAF-GERT(N(t),S(t))。

例2試畫出某體系節點i到jk的ΨA-GERT(N(t),S(t))的智能反饋網絡ΨAF-GERT(N(t),S(t))圖。

依據定義7和定義8,設計節點的反饋節點與反饋回路(圖中虛線),如圖6所示。節點i到達節點jk(k=1,2,…,K)時,均會獲得不同程度的效果值Vjk。再通過Agent反饋的Fi值來判斷下一步路徑(i,jk)的概率值。

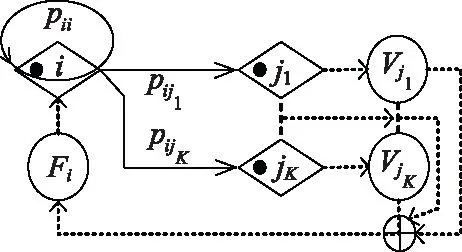
圖6 某體系節點i到jk的ΨAF-GERT(N(t),S(t))網絡結構示意圖Fig.6 Schematic diagram of ΨAF-GERT(N(t),S(t)) network structure from system node i to jk

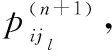
(8)

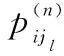
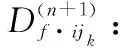
(9)

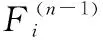
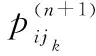
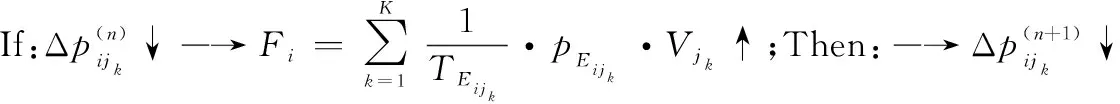
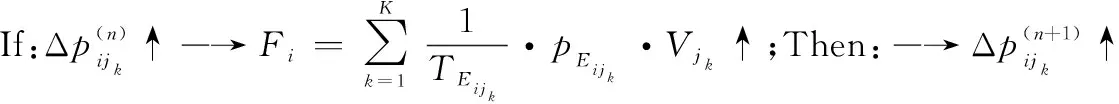
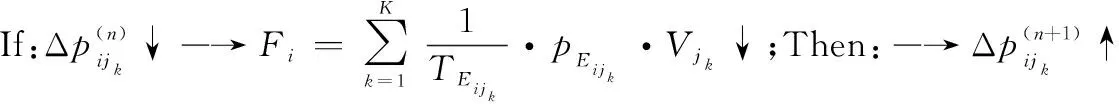
證畢

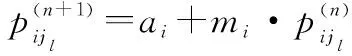
(10)

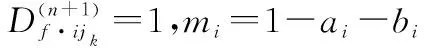
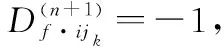
故,式(10)得證。

證畢

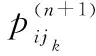
(11)

(12)

式中:ξai和ξbi分別為“正”“負”政策激勵強度系數調節參數。

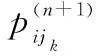
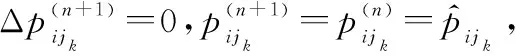
證畢

推論 2節點i中ξai和ξbi的取值:對于節點i,ξai和ξbi取值范圍滿足0≤ξbi<ξai≤1且0≤ξaiξbi≤1/4。

2014年8月20日，郭恒信又一次來到阿里甫·司馬義家中，將2000元的學費遞到兒子買買江·阿里甫手中，又一次圓了孩子上學的夢想。

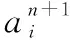
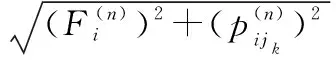
證畢

3 基于A-GERT網絡的“刺激-反應”概率學習迭代模型構建

通過對“刺激-反應”模型反饋機制的分析,進一步將AF-GERT網絡逐個分解,建立動態的迭代秩序,實現決策節點路徑概率學習的最優化。

定理 5“刺激-反應”智能學習決策動態迭代秩序:在ΨAF-GERT(N(t),S(t))網絡中,進行“刺激-反應”智能學習決策動態迭代時,保證全網絡最優的秩序是,與網絡概率傳遞方向相反,由終節點N向始節點1進行迭代,其秩序為

N→(N-1)→…→i→(i-1)→…→2→1

(13)

由于ΨAF-GERT(N(t),S(t))網絡是一種有向動態網絡,在該網絡中通過“刺激-反應”的智能學習方式進行最優路徑發現決策的本質是一個多階段動態規劃問題。運用動態規劃的Bellman原理,可構造出該問題的動態迭代秩序(見式13)。

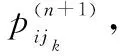
步驟 1建立Agent反饋網絡ΨAF-GERT(N(t),S(t))。

依據定義8,把定義4的ΨA-GERT(N(t),S(t))轉換成具有效用反饋結構的ΨAF-GERT(N(t),S(t))體系,如圖6所示。由于體系網絡往往由很多節點和邊構成,按照從終節點N向始節點1依次進行迭代的規則,將原始的A-GERT網絡分解為多個單一AF-GERT結構,以便后續概率迭代計算。

步驟 2建立網絡體系ΨAF-GERT(N(t),S(t))的初始假設與迭代規則。

初始條件與假設:根據已知條件,對網絡需要迭代的節點和邊進行賦值,主要包括節點活動間的傳遞概率與傳遞時間,以及終節點N效用價值的分析設定(例如體系要求評定的經濟效益、效能、利潤等指標)。

迭代秩序設計:在智能反饋網絡體系中,運用推論1進行動態迭代秩序設計,迭代秩序見圖7。

圖7 迭代程序圖Fig.7 Iterative program diagram

步驟 3第i(i∈N(t))個節點的n+1步迭代。

在對第i個節點進行路徑概率迭代時,當迭代路徑只有兩條時,可任選一條進行概率迭代;當迭代路徑大于兩條時,則任選兩條路徑進行概率學習,且此時其他路徑概率保持原始值不變,直至達到節點路徑均衡解時,即停止迭代。

(14)

當體系網絡概率學習同時考慮效用值及網絡傳遞時間時,節點i第n步和第n-1步的傳遞效用值為

(15)

根據式(6)可得:當ijk為最優路徑時,

(16)

當ijk為非最優路徑時,

(17)

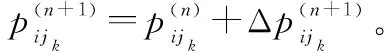
步驟 4第i(i∈N(t))個節點的智能自學習概率配置迭代解。

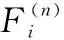
步驟 5ΨAF-GERT(N(t),S(t))的路徑智能自學習選擇最滿意解決方案。

根據圖7的“刺激-反應”學習動態迭代程序,在ΨAF-GERT(N(t),S(t))網絡體系中,按步驟3和步驟4進行各智能決策節點的逐個迭代,最終會得到該網絡路徑學習的最滿意解決方案。

證畢

4 案例研究

4.1 基于創新技術方案決策問題的A-GERT網絡“刺激-反應”學習模型構建與求解

在創新開發資源有限的情況下,根據不同目標動態選擇最優的技術開發路徑、明確資源流動方向是典型的體系活動決策問題。根據文獻[11]以及傳統的創新技術開發項目情況,依據定義4,構成的技術開發A-GERT體系網絡如圖8所示,各節點之間信息流動的傳遞函數用Wij表示。節點1表示創新技術生成與評價、節點2表示市場調研與需求預測、節點3表示項目方案總體設計、節點4、5分別表示2種新技術A、B的研究,節點6、7分別表示對新技術A、B進行試驗，節點8表示技術開發試驗成功,節點9表示技術開發試驗失敗。

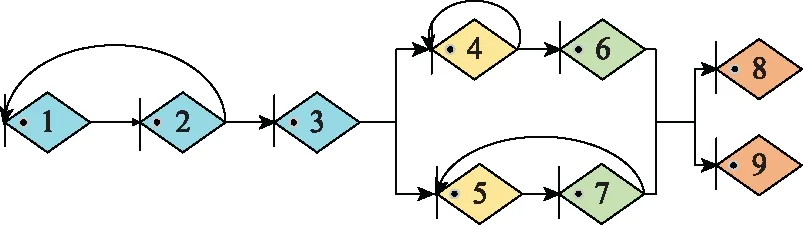
圖8 技術開發體系ΨA-GERT(N(t),S(t))網絡Fig.8 ΨA-GERT(N(t),S(t)) network of technology development system

步驟 1依據定義8,根據圖8構建的技術開發體系過程智能反饋AF-GERT網絡,如圖9所示。

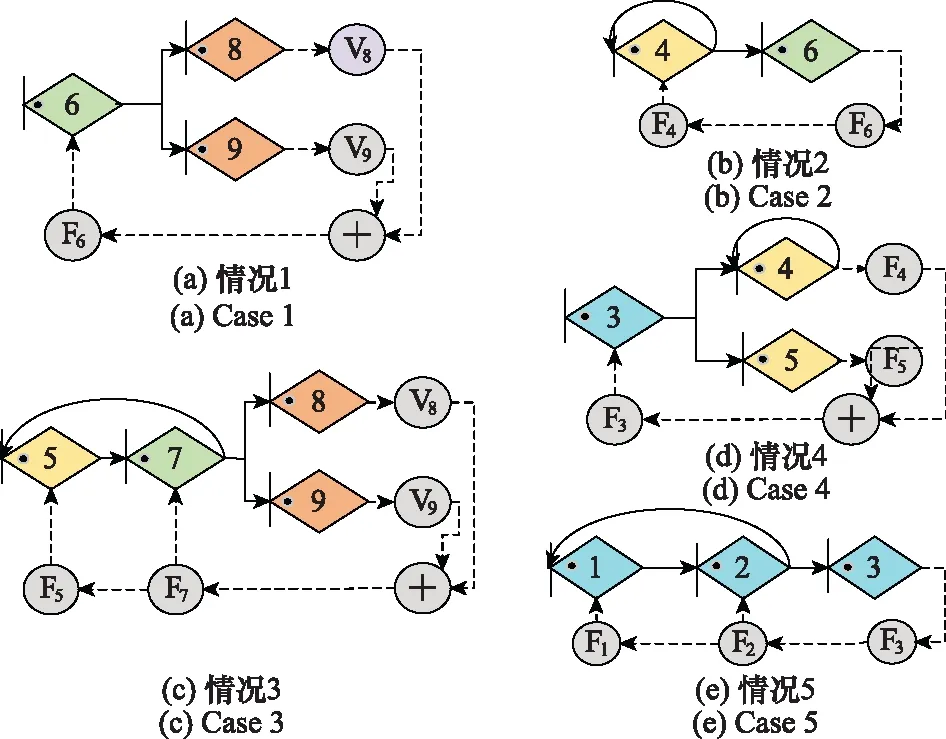
圖9 技術開發體系ΨAF-GERT(N(t),S(t))網絡Fig.9 ΨAF-GERT(N(t),S(t)) network of technology development system

步驟 2網絡體系的初始假設。

各節點間的初始概率與時間如表1所示。已知到達節點8與到達節點9分別可獲得的經濟效益為V8=200,V9=-100。每個決策節點均實施管控措施,各節點管控措施的正、負刺激因子分別為εa6=0.2,εb6=0.04;εa4=0.3,εb4=0.01;εa7=0.2,εb7=0.01;εa3=0.3,εb3=0.03;εa2=0.3,εb2=0.05。此外,設定網絡學習的初始概率增值Δp1為0.01。

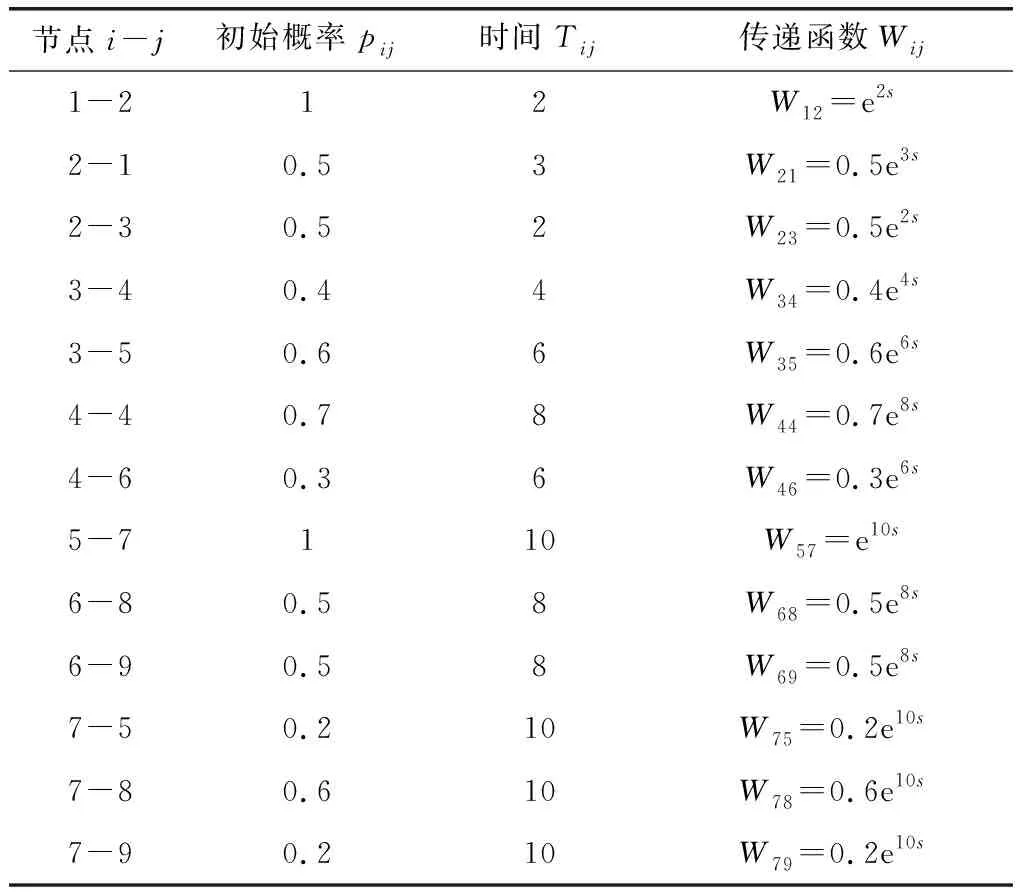
表1 活動初始傳遞概率與傳遞時間

步驟 3根據圖9所示的AF-GERT網絡依次對節點進行迭代學習。

步驟 3.1針對節點6與節點8、9間鏈路概率進行自學習。

根據定義5,節點6到節點8、9之間的等效傳遞函數WE68、WE69為WE68=W68=p68e8s和WE69=W69=p69e8s。

由式(5)、式(6)可得相應的等效傳遞概率與期望時間為pE68=p68,TE68=8和pE69=p69,TE69=8。

已知V8=200,V9=-100,當企業只考慮經濟效益影響時,由式(14)可得網絡傳遞效用值為F6=pE68×V8+pE69·V9=200p68-100p69。

當企業不僅考慮經濟效益,還考慮傳遞時間影響時,由式(15)可得網絡傳遞效用值為

根據式(16)、式(17)依次進行概率迭代學習,對節點6而言,可任選路徑概率p68和p69進行迭代,當迭代路徑概率p68時,p69=1-p68;當迭代路徑概率為p69時,p68=1-p69。迭代學習的結果如圖10所示,從中不難發現,無論迭代p68還是p69,最終的概率均衡值都相同。

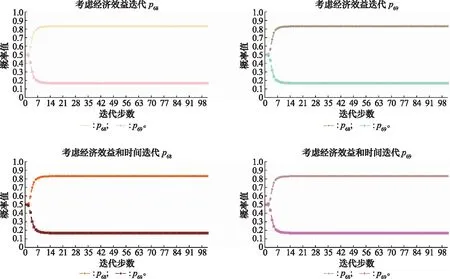
圖10 節點6迭代概率圖Fig.10 Iteration probability diagram of node 6

由此可得節點6最終的路徑學習概率為p68=0.833 3,p69=0.166 7,節點概率達到均衡狀態時,此時網絡傳遞效用值即為節點6最終的效用值。因此,當企業只追求經濟效益時,節點6最終的效用值為

V6=200×0.833 3-100×0.166 7=149.99

當企業不僅考慮經濟效益,還考慮傳遞時間影響時,網絡傳遞效用值為

步驟 3.2針對節點4與節點6間鏈路概率進行自學習 。

根據定義5,節點4到節點6之間的等效傳遞函數WE46為WE46=W46/(1-W44)=p46e6s/(1-p44e8s)

由式(5)、式(6)可得相應的等效傳遞概率與期望時間為

當企業只考慮經濟效益影響時,此時由于pE46=1,該情況由p46代替pE46進行迭代計算。節點4的傳遞效用值為F4=p46·V6=149.99p46。

當企業不僅考慮經濟效益,還考慮傳遞時間影響時,由式(15)可得節點4的傳遞效用值為

同樣根據式(16)、式(17)依次進行迭代學習,迭代學習的結果如圖11所示。

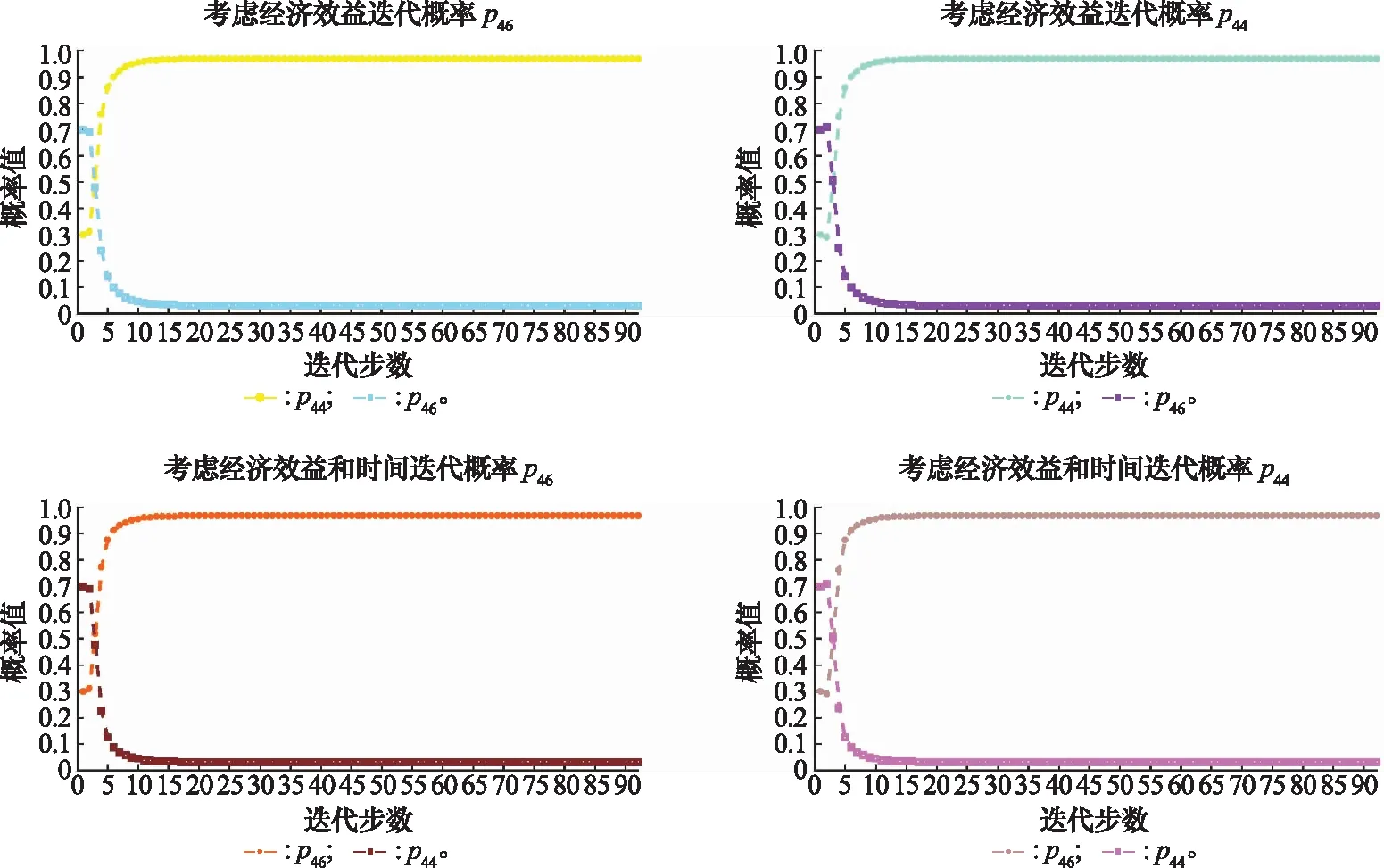
圖11 節點4迭代概率值Fig.11 Iteration probability diagram of node 4

節點4最終的路徑學習概率為p46=0.967 7,p44=0.032 3,當企業只追求經濟效益時,節點4最終的效用值V4=149.99×0.967 7=95.802 3;當企業不僅考慮經濟效益,還考慮傳遞時間影響時,節點4最終的效用值為

步驟 3.3針對節點7與節點8、9間鏈路概率進行自學習。

根據定義5,節點7到節點8、9之間的等效傳遞函數WE78、WE79為

由式(5)、式(6)可得相應的等效傳遞概率與期望時間為

當企業只追求經濟效益時,由式(14)可得節點7的傳遞效用值為F7=200p78/(1-p75)-100p79/(1-p75);當企業不僅考慮經濟效益,還考慮傳遞時間影響時,由式(15)可得節點7的傳遞效用值為F7=200pE78/TE78-100pE79/TE79=(200p78-100p79)/(10+10p75)。

根據式(16)、式(17)依次進行迭代學習,對節點7而言,可任選兩個路徑概率p75、p78和p79進行迭代,例如首先固定p78=0.6保持不變,當迭代路徑概率為p75時,p79=1-0.6-p75,然后繼續固定某路徑概率保持不變(例如p79),迭代路徑概率為p78時,p75=1-p79-p78,重復上述操作,直到路徑概率達到均衡值。迭代學習的結果如圖12所示。

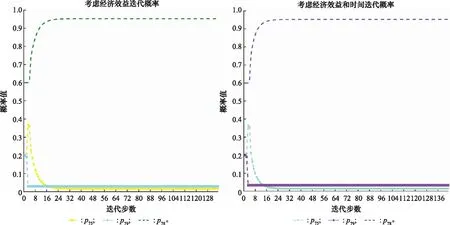
圖12 節點7迭代概率值Fig.12 Iteration probability diagram of node 7

當企業只考慮經濟效益影響時,節點7最終的效用值

此時V5=V7p57=190.690 8。

當企業不僅考慮經濟效益,還考慮傳遞時間影響時,節點7最終的效用值為

此時V5=18.455 3/10=1.845 53。

步驟 3.4針對節點3與節點4、5間鏈路概率進行自學習。

根據定義5,節點3到節點4、5之間的等效傳遞函數WE34、WE35為WE34=W34=p34T34,WE35=W35=p35T35。

由式(5)、式(6)可得相應的等效傳遞概率與期望時間為pE34=p34,pE35=p35和TE34=4,TE35=6。

當企業只追求經濟效益時,由式(14)可得節點3的效用值為

F3=p34V4+p35V5=95.802 3p34+190.690 8p35

當企業不僅考慮經濟效益,還考慮傳遞時間影響時,由式(15)可得節點3的效用值為

根據式(16)、式(17)依次進行迭代學習,對節點3而言,可任選路徑概率p34和p35進行迭代,迭代學習的結果如圖13所示。

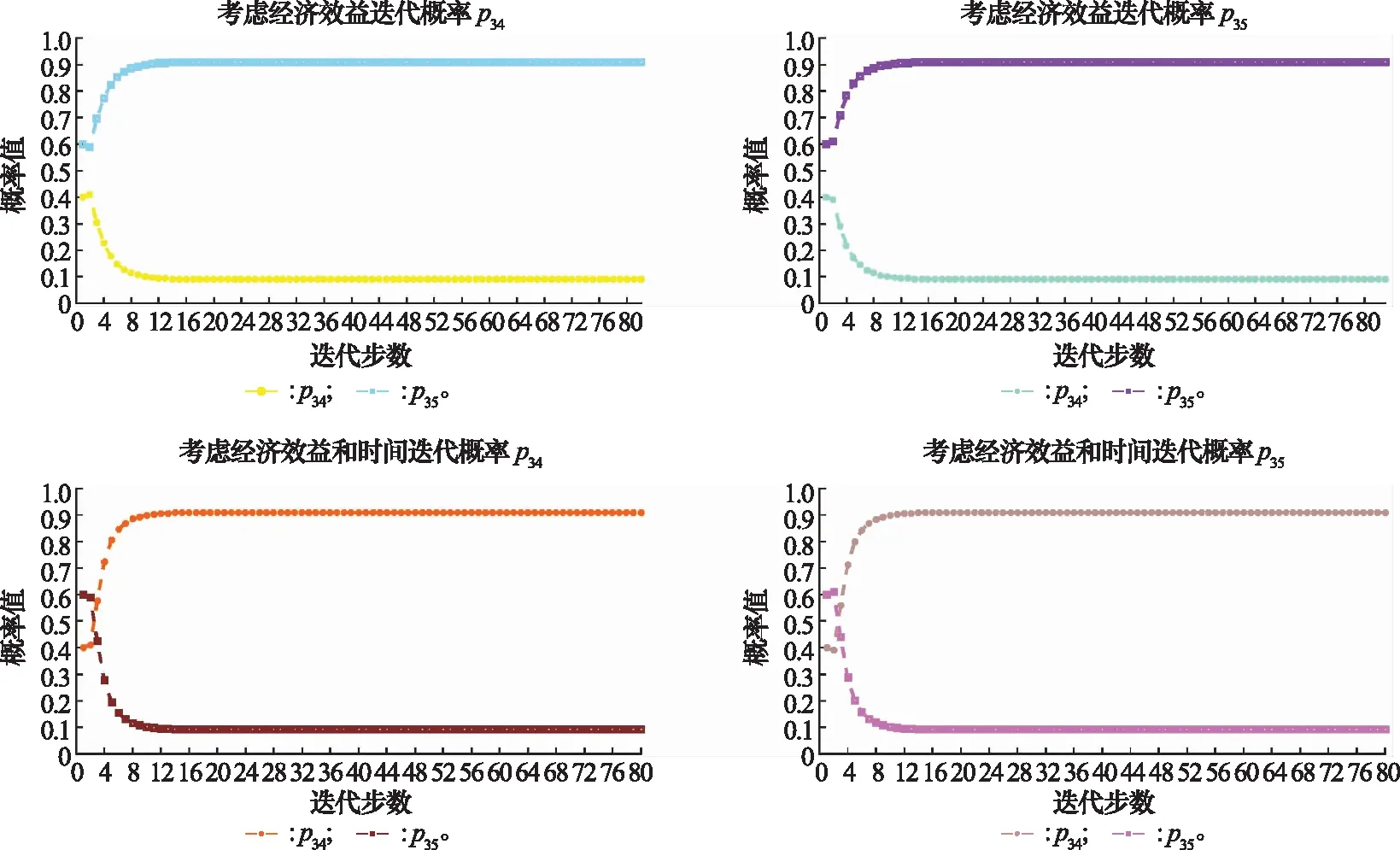
圖13 節點3迭代概率值Fig.13 Iteration probability diagram of node 3

由此可得當企業只追求經濟效益時,節點3最終的效用值

V3=95.802 3×0.090 9+190.690 8×0.909 1=182.065 4

當企業不僅考慮經濟效益,還考慮傳遞時間影響時,節點3最終的效用值為

步驟 3.5針對節點2與節點3間鏈路概率進行自學習。

根據定義5,節點2到節點3之間的等效傳遞函數為WE23=W23/(1-W12W21)=p23e2s/(1-p21e5s)。

由式(5)、式(6)相應的等效傳遞概率與期望時間為pE23=p23/(1-p21),TE23=(1/pE23)·(?WE23/?s|s=0)=(2+3p21)/p23;當企業只追求經濟效益時,由式(14)可得節點2的傳遞效用值為F2=182.065 4p23。

當企業不僅考慮經濟效益,還考慮傳遞時間影響時,由式(15)可得節點2的傳遞效用值為F2=pE23V3/TE23=0.707 9p23/(2+3p21)。

根據式(16)、式(17)依次進行迭代學習,對節點2而言,可任選路徑概率p23和p21進行迭代,迭代學習的結果如圖14所示。

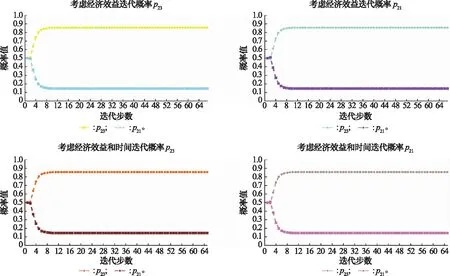
圖14 節點2迭代概率值Fig.14 Iteration probability diagram of node 2

步驟 4各節點路徑概率配置均衡解。

節點6、4、7最優的路徑學習概率為p68=0.833 3,p46=0.967 7,p78=0.952 4;節點3最優的路徑學習概率有兩種情況,當只考慮經濟效益時,p35=0.909 1,當考慮經濟效益和時間時,p34=0.909 1;節點2最優的路徑學習概率為p23=0.857 1。

步驟 5技術開發體系網絡最優路徑方案決策。

綜上,當傳遞效用值只考慮經濟效益驅動影響時,網絡決策的最優路徑為1-2-3-5-7-8;當考慮經濟效益和完成時間影響時,網絡決策的最優路徑為1-2-3-4-6-8;并且智能節點經過學習,回路路徑的傳遞概率大大減少,資源配置效率也相應提高。當系統主體只追求經濟效益時,創新開發資源將逐漸流向技術B的開發,而當系統主體既考慮經濟效益,又考慮完工時間時,創新開發資源將逐漸流向技術A的開發。

4.2 參數敏感性分析

文中涉及的參數主要包括初始概率增值Δp1以及刺激因子ξa、ξb,其中參數Δp1是啟動迭代方程的引子,并不影響節點最終的概率均衡值。以節點6為例,對Δp1進行敏感度分析以說明其影響。

由圖15可知,對于不同的初始概率增值Δp1=0.001,0.01,0.1,0.2,0.3,0.4,最終的概率均衡值不變,迭代步數也僅差1～2步。因此,Δp1的取值并不影響迭代過程。理論上,Δp1≤1-p0,但實際應用過程中,Δp1值不宜過大,否則不符合現實初始概率增加的情況,建議取值范圍為0<Δp1≤0.1。

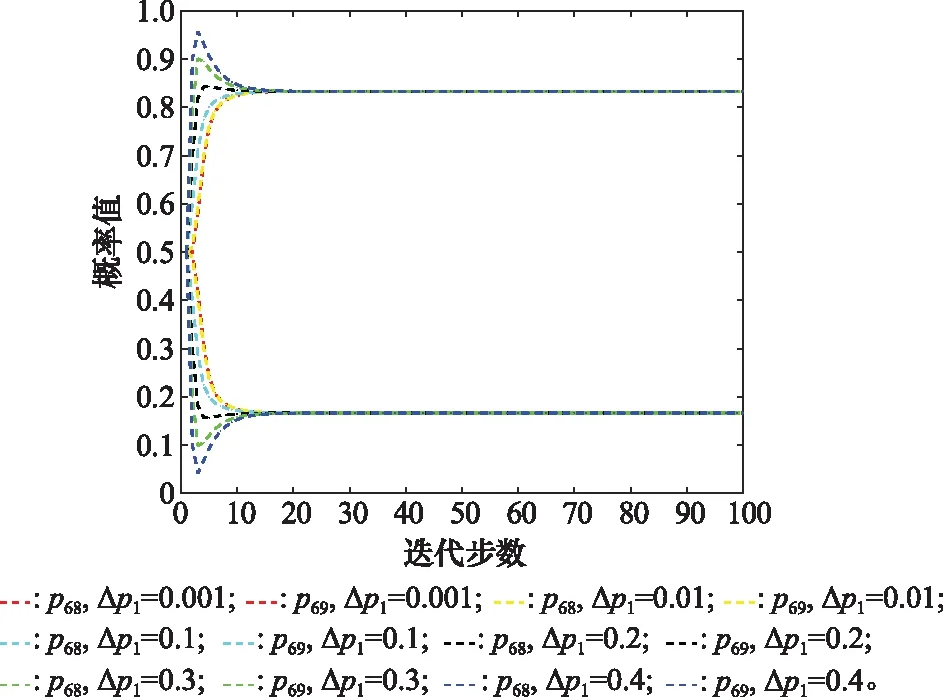
圖15 節點6不同Δp1的敏感性分析Fig.15 Sensitivity analysis of different Δp1 for node 6

由推論2可知,正、負刺激因子的取值范圍為0≤ξbi<ξai≤1且0≤ξaiξbi≤1/4。由定理4可知,均衡解為ξai/ξai+ξbi=ξai/ξbi/(1+ξai/ξbi),因此為了研究刺激因子的具體影響,針對不同的ξai/ξbi值,對節點刺激因子進行靈敏度分析,如圖16～圖18所示。

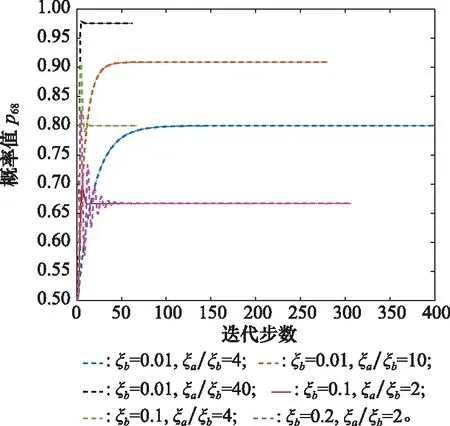
圖16 節點6不同ξa和ξb的敏感性分析Fig.16 Sensitivity analysis of different ξa and ξb for node 6

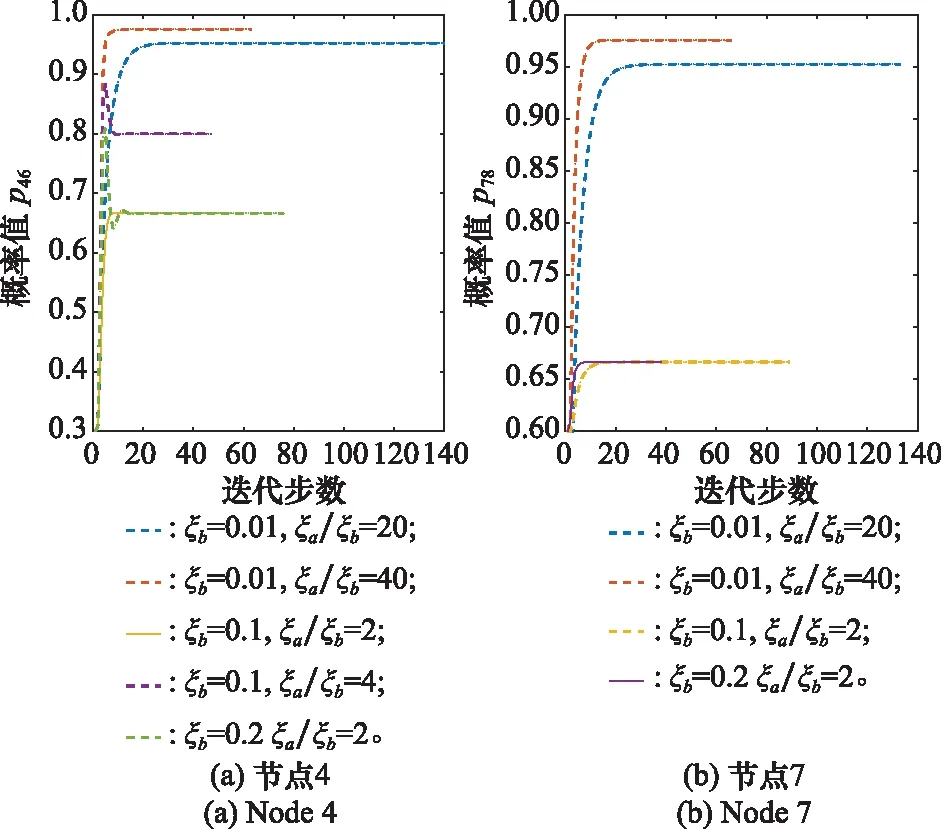
圖17 節點4和7不同ξa和ξb的敏感性分析Fig.17 Sensitivity analysis of different ξa and ξb for nodes 4 and 7

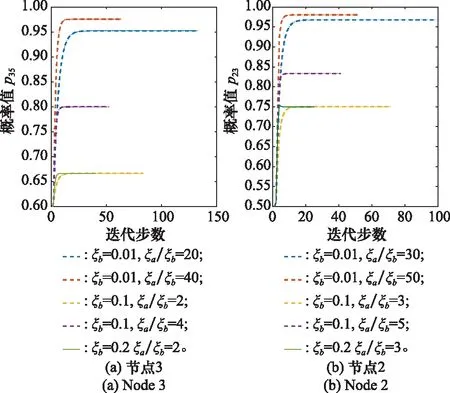
圖18 節點2和3不同ξa和ξb的敏感性分析Fig.18 Sensitivity analysis of different ξaand ξb for nodes 2 and 3

由圖16～圖18所示,對于相同的ξb,ξai/ξbi的值越大,最優路徑最終迭代的概率均衡值越大。這說明正刺激相對于負刺激的效應越大,最終的迭代效果也就越好。此外,對于相同的ξai/ξbi值,ξb越大,迭代曲線的波動會更大,這可能是因為負刺激因子的作用在破壞概率改進的過程。因此在實際應用過程中,應努力促進正刺激因子的改善,避免負刺激的產生。

4.3 對比分析

本節通過3種方式(不學習、固定激勵系數學習、變激勵系數學習)進行效果分析,其中固定激勵系數學習指的是學習迭代方程中不考慮效用值的驅動影響,但學習迭代方程中仍保留方向函數的存在,方向函數保證了迭代方向的正確,如若不考慮方向函數,則在迭代錯誤路徑概率時,該路徑概率也會一直增加。由于迭代過程中涉及迭代步數以及迭代概率兩個關鍵值,因此分別從達到均衡概率值的迭代步數以及迭代步數相同時迭代路徑的概率兩個角度進行對比分析。其中a表示固定激勵系數學習(考慮經濟效益);b表示固定激勵系數學習(考慮經濟效益和時間);c表示變激勵系數學習(考慮經濟效益);d表示變激勵系數學習(考慮經濟效益和時間)。

(1) 迭代步數對比分析

如表2以及圖19所示,傳遞效用值無論是否考慮活動時間,變激勵系數學習都比固定激勵學習的迭代步數要少,說明考慮目標效益驅動影響可以加快學習迭代的速度。

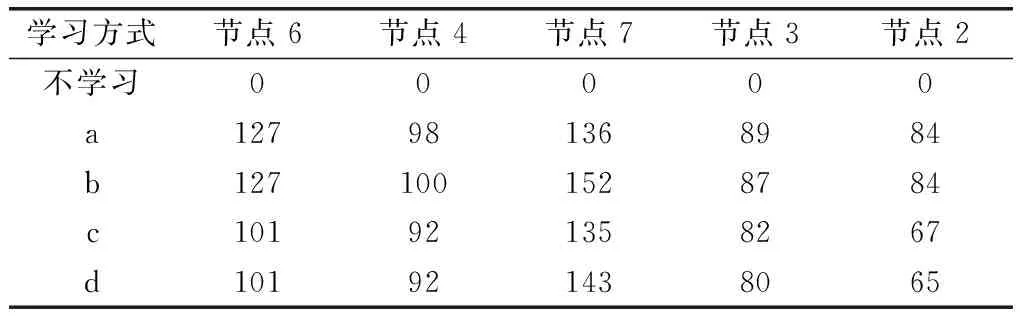
表2 達到均衡解時的迭代步數對比

圖19 迭代步數對比圖Fig.19 Comparison diagram of iteration steps

(2) 迭代概率對比分析

為便于節點迭代路徑概率的比較,不同學習方式取相同的迭代步數。例如,在變激勵學習中節點6到節點8、9之間的路徑概率迭代到第23步時,p68=0.833 3,p69=0.166 7,因此在固定激勵系數學習中,取第23步時的路徑迭代概率進行比較。不同學習方式的最優路徑概率以及創新技術開發項目成功的期望概率、期望時間對比如表3所示。

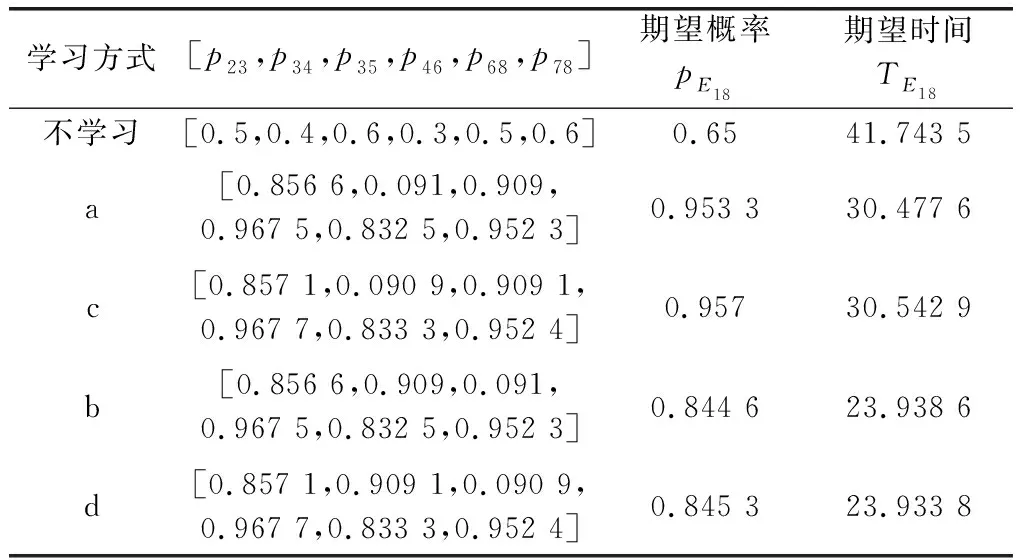
表3 不同學習方式迭代概率對比

根據表3可以看出,一方面,與不學習相比,經過學習后的最優路徑概率均有不同程度的增加,成功的期望概率是不學習的1.3到1.47倍,完工時間也縮短了26.99%到42.66%。另一方面,當系統目標只考慮經濟效益影響時,變激勵系數學習比固定激勵系數學習效果略有提高,成功的期望概率是固定激勵系數學習的1.003 5倍;當系統目標考慮經濟效益與完工時間影響時,變激勵系數學習成功的期望概率是固定激勵系數學習的1.001倍,完工時間縮短了0.02%。因此,變激勵系數學習方式無論是在迭代步數還是迭代概率方面均有不同程度的改進。

(3) 與其他方法對比分析

文獻[11]給出了GERT網絡多目標決策的資源優化求解方法,與本文相比,文獻[11]雖然改善了網絡節點傳遞概率,指明了資源流動方向,但網絡不具備學習能動性。經過案例數據計算,路徑概率對比如表4所示,利用本文方法,最終的期望概率可提高10.89%,期望時間縮短26%。

表4 與其他方法迭代概率對比

綜上所述,通過自身學習方式以及其他方法的對比分析,驗證了基于A-GERT網絡“刺激-反應”學習模型的合理性和有效性。

5 結束語

本文主要研究基于GERT網絡的體系過程決策問題,例如在工程計劃管理、產業價值流動以及作戰編配體系等需要在不同階段做出最優決策的體系活動中,GERT網絡雖然可以很好地描述活動過程,但網絡節點的決策模式較為靜態單一,無法體現活動過程中決策的能動性。因此,首先以GERT網絡為基礎架構,構建Agent系過程A-GERT網絡,結合改進的刺激-反應模型研究體系網絡活動的概率學習機制。刺激-反應模型可通過輸出反饋進行主動學習,具有良好的自適應性。此外,從目標效益驅動的角度出發,通過計算網絡傳遞效用值改進刺激-反應學習迭代方程,構建A-GERT網絡“刺激-反應”模型的學習決策機制。最后,以技術開發方案決策問題進行分析研究,結果表明,在管控措施激勵以及不同的目標效益驅動下,傳遞概率會產生相應的動態變化,資源也會流向更優的技術開發路徑。并且通過對比分析,該模型的效果更好。A-GERT網絡“刺激-反應”模型的構建為解決體系網絡過程學習決策問題提供了一種新思路。