基于擾動(dòng)觀測(cè)器的飛行器軌跡跟蹤控制器設(shè)計(jì)

李傳旭, 孟秀云,*, 王 捷

(1. 北京理工大學(xué)宇航學(xué)院, 北京 100081; 2. 北京電子工程總體研究所, 北京 100854)

0 引 言

隨著飛行器作戰(zhàn)任務(wù)的日益多樣化和復(fù)雜化,為提升飛行器的飛行性能,往往需要飛行器按照預(yù)設(shè)的優(yōu)化軌跡進(jìn)行飛行,比如固定翼飛行器的棲落機(jī)動(dòng)[1-3]、高超聲速飛行器的再入軌跡跟蹤[4-5]等。然而飛行器在飛行過程中會(huì)受到多種擾動(dòng)因素的影響,導(dǎo)致實(shí)際的飛行軌跡偏離參考軌跡,因此需要設(shè)計(jì)軌跡跟蹤控制器確保飛行器在擾動(dòng)作用下仍能精確跟蹤參考軌跡。一般情況下,參考軌跡是隨時(shí)間變化的位置信息,軌跡跟蹤控制的目的是使飛行器能夠在相應(yīng)時(shí)間精確運(yùn)動(dòng)到對(duì)應(yīng)位置上[6]。

現(xiàn)有的飛行器軌跡跟蹤控制方法從設(shè)計(jì)思路上可大體分為兩類。第一類方法是通過在參考軌跡上設(shè)置移動(dòng)的虛擬目標(biāo)點(diǎn),將軌跡跟蹤問題轉(zhuǎn)換為制導(dǎo)問題,通過設(shè)計(jì)制導(dǎo)律控制飛行器追蹤目標(biāo)點(diǎn),間接實(shí)現(xiàn)對(duì)參考軌跡的跟蹤。文獻(xiàn)[7-8]使用速度追蹤法跟蹤虛擬目標(biāo)點(diǎn),并設(shè)計(jì)了無人機(jī)的多回路控制結(jié)構(gòu)。文獻(xiàn)[9]在視線角法的基礎(chǔ)上引入了一種修正的非線性擾動(dòng)觀測(cè)器(modified nonlinear disturbance observer,MNDO),提升了無人飛艇跟蹤軌跡時(shí)的抗干擾能力。文獻(xiàn)[10]使用彈道成型的方法,采用帶有攻擊角約束彈道成型制導(dǎo)律進(jìn)行跟蹤,降低了跟蹤過程的需用過載。文獻(xiàn)[11-12]提出了一種非線性制導(dǎo)律,具有較好的曲線跟蹤能力,文獻(xiàn)[3]將該方法應(yīng)用于飛行器棲落軌跡的跟蹤。文獻(xiàn)[13]提出了一種基于虛擬力的制導(dǎo)律,使無人機(jī)在跟蹤軌跡的同時(shí)進(jìn)行障礙規(guī)避。文獻(xiàn)[14]設(shè)計(jì)了一種基于終端滑模和動(dòng)態(tài)面控制的軌跡跟蹤制導(dǎo)律,具有較好的魯棒性。這一類方法能夠較好地控制飛行器沿著參考軌跡對(duì)應(yīng)的曲線飛行,但受虛擬目標(biāo)點(diǎn)選取方式的影響,難以充分利用參考軌跡中的時(shí)間信息,較難保證飛行器在相應(yīng)時(shí)間到達(dá)對(duì)應(yīng)位置。第二類方法是基于飛行器當(dāng)前時(shí)刻的位置誤差設(shè)計(jì)控制律直接進(jìn)行軌跡跟蹤控制,由于實(shí)時(shí)的位置誤差包含了時(shí)間信息,這類方法可以實(shí)現(xiàn)位置和時(shí)間的精確跟蹤。目前已有不少學(xué)者基于多種控制理論設(shè)計(jì)了軌跡跟蹤控制器,如比例積分微分控制[2,15]、線性二次型調(diào)節(jié)控制[5,16]、模型預(yù)測(cè)控制[17-21]、變結(jié)構(gòu)控制[4,22-25]等。文獻(xiàn)[19]基于多級(jí)模型預(yù)測(cè)控制方法實(shí)現(xiàn)了旋翼無人機(jī)的軌跡跟蹤。文獻(xiàn)[21]使用無偏模型預(yù)測(cè)技術(shù),提升了涵道風(fēng)扇無人機(jī)軌跡跟蹤控制的魯棒性。滑模變結(jié)構(gòu)控制(sliding mode control,SMC)在系統(tǒng)模型存在不確定性和外界擾動(dòng)等因素具有較好的魯棒性,且對(duì)非線性系統(tǒng)有較好的控制效果,因此被廣泛應(yīng)用于軌跡跟蹤控制。文獻(xiàn)[4]設(shè)計(jì)了自適應(yīng)滑模控制器用于高超聲速飛行器的縱向軌跡跟蹤。文獻(xiàn)[22]使用模糊邏輯系統(tǒng)近似的滑模控制方法實(shí)現(xiàn)了平流層衛(wèi)星的軌跡跟蹤。文獻(xiàn)[24]基于自適應(yīng)終端滑模控制理論設(shè)計(jì)了水下航行器的深度跟蹤控制器。文獻(xiàn)[25]運(yùn)用自適應(yīng)反步滑模方法設(shè)計(jì)了欠驅(qū)動(dòng)飛艇的軌跡跟蹤控制器,具有良好的抗干擾能力。

現(xiàn)有的飛行器軌跡跟蹤控制方法主要研究的是二維平面內(nèi)軌跡跟蹤問題,而對(duì)三維軌跡跟蹤問題的研究相對(duì)較少。三維軌跡跟蹤控制器的設(shè)計(jì)需要考慮飛行器產(chǎn)生機(jī)動(dòng)力方式,固定翼飛行器主要采用傾斜轉(zhuǎn)彎(bank-to-turn,BTT)的控制方式,通過滾轉(zhuǎn)運(yùn)動(dòng)改變升力面的方向從而產(chǎn)生側(cè)向過載,實(shí)現(xiàn)轉(zhuǎn)彎?rùn)C(jī)動(dòng)。對(duì)于滑模控制方法,終端滑模(terminal sliding mode, TSM)相較傳統(tǒng)線性滑模面具有有限時(shí)間收斂的優(yōu)點(diǎn),非奇異TSM(nonsingular TSM, NTSM)控制解決了TSM存在的控制指令奇異問題。為進(jìn)一步解決NTSM在系統(tǒng)遠(yuǎn)離平衡點(diǎn)時(shí)收斂較慢的問題,文獻(xiàn)[26-27]提出了非奇異快速終端滑模控制(nonsingular fast TSM, NFTSM)方法,對(duì)于提升軌跡跟蹤控制器性能具有較大應(yīng)用價(jià)值。

本文針對(duì)多種擾動(dòng)作用下的固定翼飛行器三維軌跡跟蹤問題,首先建立BTT控制方式下的飛行器三維軌跡跟蹤誤差模型,為增強(qiáng)軌跡跟蹤控制器的抗干擾能力,在非線性擾動(dòng)觀測(cè)器的基礎(chǔ)上引入狀態(tài)估計(jì)誤差反饋,提升對(duì)時(shí)變擾動(dòng)的估計(jì)能力。為進(jìn)一步提升軌跡跟蹤控制器的快速性,基于NFTSM方法,采用雙冪次趨近律設(shè)計(jì)三維軌跡跟蹤控制器。最后,結(jié)合實(shí)際工程應(yīng)用對(duì)本文設(shè)計(jì)的軌跡跟蹤控制器進(jìn)行仿真分析。

1 問題描述與模型建立

對(duì)于BTT控制方式的飛行器,在理想情況下其側(cè)滑角為零,滾轉(zhuǎn)角近似等于速度傾斜角,并考慮到在常規(guī)飛行條件下發(fā)動(dòng)機(jī)推力主要影響飛行速度的大小,對(duì)速度方向的影響較小,因此在建模時(shí)將推力的影響作近似處理,將建模誤差視為擾動(dòng)項(xiàng)。基于上述條件,得到BTT飛行器三維質(zhì)心運(yùn)動(dòng)方程組為

(1)

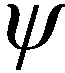
(2)

式中:CD為阻力系數(shù);Sref為參考面積;ρ為大氣密度。

已知參考軌跡xd(t)、yd(t)、zd(t)為隨時(shí)間變化的三維空間位置,軌跡跟蹤的目標(biāo)是控制飛行器的質(zhì)心在相應(yīng)時(shí)間精確運(yùn)動(dòng)到對(duì)應(yīng)的位置。下面建立BTT飛行器三維軌跡跟蹤誤差模型。定義當(dāng)前時(shí)刻飛行器x、y、z3個(gè)方向的軌跡跟蹤誤差分別為

(3)

為表明控制輸入與軌跡跟蹤誤差的關(guān)系,對(duì)其沿時(shí)間求二階導(dǎo)數(shù),將式(1)代入,得到軌跡跟蹤誤差模型為

(4)

式中:L為旋轉(zhuǎn)矩陣,其表達(dá)式為

(5)

2 擾動(dòng)觀測(cè)器設(shè)計(jì)

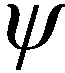
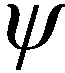
2.1 非線性擾動(dòng)觀測(cè)器

對(duì)于一般一階非線性系統(tǒng)：

(6)

式中:x為系統(tǒng)的狀態(tài)變量;f(x)和g(x)為已知非線性函數(shù);u為控制量;d為未知擾動(dòng)項(xiàng)。NDO的一般形式如下[28]:

(7)

(8)

(9)

2.2 基于狀態(tài)估計(jì)誤差反饋的擾動(dòng)觀測(cè)器設(shè)計(jì)

為提高NDO對(duì)時(shí)變擾動(dòng)的估計(jì)能力,在NDO的基礎(chǔ)上引入狀態(tài)估計(jì)誤差反饋,設(shè)計(jì)改進(jìn)的NDO(improved NDO, INDO)。

(10)

(11)

(12)

(13)

為保證擾動(dòng)觀測(cè)器穩(wěn)定,系統(tǒng)的特征根應(yīng)具有負(fù)實(shí)部,所以擾動(dòng)觀測(cè)器的設(shè)計(jì)參數(shù)應(yīng)滿足l>0且k>0。相較于傳統(tǒng)NDO,INDO可以無靜差地跟蹤斜坡輸入,具有更好的估計(jì)時(shí)變擾動(dòng)的能力。

3 三維軌跡跟蹤控制器設(shè)計(jì)

3.1 基于雙冪次趨近律的NFTSM控制方法

考慮如下含未知擾動(dòng)的二階非線性單輸入單輸出(single input single output,SISO)系統(tǒng):

(14)

式中:x=[x1,x2]T為系統(tǒng)狀態(tài)量;u為控制輸入;d為未知擾動(dòng);y為系統(tǒng)輸出;f(x,t)和g(x,t)為已知函數(shù)。

為使系統(tǒng)狀態(tài)在有限時(shí)間收斂,并在避免控制量奇異的同時(shí)提升系統(tǒng)遠(yuǎn)離平衡點(diǎn)時(shí)的收斂速度,選取NFTSM滑模面[27]為

(15)

式中：設(shè)計(jì)參數(shù)m,n,p,q均為正奇數(shù),并且滿足1

p/q;α,β∈R+。對(duì)于被控對(duì)象(14),當(dāng)系統(tǒng)處于滑動(dòng)模態(tài)時(shí),系統(tǒng)狀態(tài)能夠在有限時(shí)間收斂。

為保證系統(tǒng)能夠在有限時(shí)間到達(dá)滑動(dòng)平面,并進(jìn)一步提升收斂速度,同時(shí)避免系統(tǒng)抖振,采用雙冪次趨近律[29]。由于選取的是NFTSM滑模面,為避免控制律中出現(xiàn)負(fù)指數(shù)項(xiàng)導(dǎo)致控制律奇異,對(duì)雙冪次趨近律進(jìn)行調(diào)整,得到如下趨近律:

(16)

其中,設(shè)計(jì)參數(shù)k1>0,k2>0,γ1>1,0<γ2<1。

對(duì)滑模函數(shù)s求導(dǎo)可得

(17)

(18)

控制律中的k1|s|γ1sgns項(xiàng)和k2|s|γ2sgns項(xiàng)均為連續(xù)函數(shù),因此能夠避免由非連續(xù)切換項(xiàng)導(dǎo)致的抖振問題。

3.2 穩(wěn)定性分析

(19)

式中:V(x0)為V(x)的初值。

(20)

證明構(gòu)造Lyapunov函數(shù)

V=0.5s2

對(duì)其沿時(shí)間求導(dǎo)可得

(21)

將控制律(18)代入式(21),可得

(22)

(23)

(24)

經(jīng)變形可得

(25)

(26)

已知0<γ2<1,則0.5<(γ2+1)/2<1,根據(jù)引理1可知,系統(tǒng)能在有限時(shí)間內(nèi)收斂到區(qū)域

(27)

證畢

3.3 INDO-NFTSM三維軌跡跟蹤控制器設(shè)計(jì)

飛行器在三維空間中的質(zhì)心運(yùn)動(dòng)本質(zhì)上為質(zhì)點(diǎn)的三維運(yùn)動(dòng)問題。對(duì)于三維空間中的質(zhì)點(diǎn),若其控制輸入為慣性坐標(biāo)系三軸的加速度,則它在慣性坐標(biāo)系中3個(gè)方向的運(yùn)動(dòng)是相互獨(dú)立的。

由于飛行器的軌跡跟蹤誤差是在慣性坐標(biāo)系中描述的,為了將軌跡跟蹤控制器從x、y、z3個(gè)方向分開進(jìn)行設(shè)計(jì),給出慣性坐標(biāo)系三軸加速度與BTT控制方式下飛行器的控制量推力P、法向加速度ay、滾轉(zhuǎn)角γ的轉(zhuǎn)換關(guān)系。定義3個(gè)中間控制量ux、uy、uz,并定義dx、dy、dz3個(gè)中間擾動(dòng)項(xiàng),表達(dá)式為

(28)

中間控制量ux、uy、uz的實(shí)際物理含義為飛行器加速度在慣性坐標(biāo)系3個(gè)方向的分量。由此可將式(4)改寫為

(29)

若將中間控制量視為控制輸入,將跟蹤誤差視為輸出,則可將三維軌跡跟蹤誤差模型按x、y、z方向分解為3個(gè)相互獨(dú)立的如式(14)的二階SISO子系統(tǒng)。

根據(jù)式(15),對(duì)于分解后的3個(gè)子系統(tǒng)分別選取NFTSM滑模面,各方向的參數(shù)用下標(biāo)x、y、z加以區(qū)分,滑模面形式為

(30)

(31)

最后根據(jù)式(28)對(duì)中間控制量進(jìn)行變換,得到BTT飛行器三維軌跡跟蹤控制律為

(32)

其中,T1、T2、T3為中間量,表達(dá)式為

(33)

4 仿真結(jié)果與分析

本文采用的固定翼飛行器基本參數(shù)為:M=300 kg,Sref=0.06 m2,CD=0.5。考慮實(shí)際飛行條件限制,采用BTT-45控制方式,限制滾轉(zhuǎn)角指令γcmd范圍在±45°范圍內(nèi),限制可用推力范圍為300～1 500 N;可用法向加速度范圍為±40 m/s2。考慮到飛行器姿態(tài)回路和發(fā)動(dòng)機(jī)的工作特性,仿真時(shí)將飛行器對(duì)推力指令、法向加速度指令和滾轉(zhuǎn)角指令的響應(yīng)過程等效為二階振蕩環(huán)節(jié):推力控制回路的自然頻率為15 rad/s,阻尼比為0.9;法向過載控制回路的自然頻率為25 rad/s,阻尼比為0.8;滾轉(zhuǎn)角控制回路的自然頻率為30 rad/s,阻尼比為0.8。

在INDO-NFTSM三維軌跡跟蹤控制器中:滑模面參數(shù)選取為:αx=6,βx=0.8,αy=5,βy=1,αz=6,βz=0.8,mx=my=mz=7,nx=ny=nz=3,px=py=pz=5,qx=qy=qz=3;趨近律參數(shù)選取為:k1x=0.1,k2x=0.8,k1y=0.2,k2y=1.2,k1z=0.1,k2z=0.8,γ1x=γ1y=γ1z=1.5,γ2x=γ2y=γ2z=0.5。

選取文獻(xiàn)[28]提出的NDO與文獻(xiàn)[9]提出的MNDO進(jìn)行對(duì)比仿真分析。為確保3種擾動(dòng)觀測(cè)器具有相近的響應(yīng)速度,選取NDO的參數(shù)為lNDO=17.5,MNDO的參數(shù)為lMNDO=12.5,kMNDO=19.5,INDO的參數(shù)為lINDO=32,kINDO=400。

4.1 勻速直線軌跡跟蹤

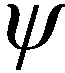
參考勻速直線軌跡保持1 000 m的飛行高度,飛行速度大小為200 m/s,速度方向朝x正方向。

仿真結(jié)果如圖1和圖2所示。

圖1 勻速直線軌跡跟蹤誤差曲線Fig.1 Tracking error curve of uniform linear trajectory

圖2 勻速直線軌跡跟蹤控制量變化曲線Fig.2 Control input curve of uniform linear trajectory

從圖1中可以看出,在多種擾動(dòng)的綜合作用下,INDO-NFTSM三維軌跡跟蹤控制器能較好地控制飛行器跟蹤勻速直線參考軌跡,x、y、z3個(gè)方向的跟蹤誤差均能夠快速收斂至0附近,且超調(diào)量較小,x方向最大跟蹤誤差為0.006 m,y、z方向最大跟蹤誤差為0.02 m,系統(tǒng)具有較高的跟蹤精度和良好的魯棒性。采用MNDO的跟蹤精度略微高于NDO,兩者在x方向的最大跟蹤誤差均在0.01 m附近,y、z方向最大跟蹤誤差均在0.05 m附近。說明在時(shí)變擾動(dòng)作用下,采用INDO的跟蹤精度明顯高于NDO和MNDO,且過渡過程平緩。

從圖2中可以看出,軌跡跟蹤控制器能夠控制飛行器持續(xù)機(jī)動(dòng)以減弱外界擾動(dòng)的影響。同時(shí)可以發(fā)現(xiàn)由于采用了雙冪次趨近律,推力、法向加速度、滾轉(zhuǎn)角3個(gè)控制指令均沒有出現(xiàn)明顯的抖振現(xiàn)象。

圖3 擾動(dòng)估計(jì)誤差曲線Fig.3 Disturbance estimation error curve

4.2 空間機(jī)動(dòng)軌跡跟蹤

參考軌跡的初始高度為1 000 m,初始速度為150 m/s,速度方向朝x正方向,加速度為1 m/s2,爬升速度傾角為5°,側(cè)向蛇形機(jī)動(dòng)周期為25 s,最大需用滾轉(zhuǎn)角為35°。

仿真結(jié)果如圖4～圖7所示。

圖4 空間機(jī)動(dòng)飛行軌跡Fig.4 Maneuvering flight trajectory

圖5 空間機(jī)動(dòng)軌跡跟蹤誤差曲線Fig.5 Tracking error curve of maneuvering trajectory

從圖4和圖5中可以看出,在同時(shí)存在初始位置偏差和航向偏差的情況下,飛行器能夠快速修正誤差進(jìn)行蛇形機(jī)動(dòng)爬升,跟蹤誤差能夠收斂至0附近。采用NDO時(shí),x方向最大跟蹤誤差為0.04 m,y方向?yàn)?.022 m,z方向?yàn)?.14 m;采用MNDO時(shí),x方向最大跟蹤誤差為0.02 m,y方向?yàn)?.02 m,z方向?yàn)?.07 m;采用INDO時(shí),x方向最大跟蹤誤差為0.013 m,y方向?yàn)?.017 m,z方向?yàn)?.04 m。在圖7中,由于初始狀態(tài)落后于參考軌跡,飛行器需要先額外加速進(jìn)行追蹤,在跟蹤上參考軌跡后,飛行器能夠保持1 m/s2的加速度進(jìn)行勻加速飛行,與參考軌跡要求相同。

圖6 空間機(jī)動(dòng)軌跡跟蹤控制量變化曲線Fig.6 Control input curve of maneuvering trajectory

圖7 飛行速度大小變化曲線Fig.7 Flight velocity curve

采用INDO時(shí)飛行器的軌跡跟蹤誤差明顯小于NDO和MNDO。說明在擾動(dòng)作用下,INDO-NFTSM三維軌跡跟蹤控制器對(duì)于空間機(jī)動(dòng)軌跡仍具有良好的跟蹤能力。

5 結(jié) 論

本文針對(duì)多種擾動(dòng)影響下的固定翼飛行器三維軌跡跟蹤問題,設(shè)計(jì)了一種基于改進(jìn)非線性擾動(dòng)觀測(cè)器的非奇異快速終端滑模三維軌跡跟蹤控制器。首先推導(dǎo)了BTT控制下的飛行器三維軌跡跟蹤誤差模型,然后設(shè)計(jì)了基于狀態(tài)估計(jì)誤差反饋的INDO觀測(cè)器對(duì)系統(tǒng)的綜合擾動(dòng)進(jìn)行觀測(cè)。之后基于NFTSM控制方法,使用雙冪次趨近律設(shè)計(jì)了三維軌跡跟蹤控制器,并證明了閉環(huán)控制系統(tǒng)的穩(wěn)定性。最后分別使用勻速直線軌跡和蛇形爬升機(jī)動(dòng)軌跡檢驗(yàn)本文設(shè)計(jì)的軌跡跟蹤控制器性能。仿真結(jié)果表明,本文設(shè)計(jì)的INDO觀測(cè)器能夠較好地觀測(cè)時(shí)變擾動(dòng),在系統(tǒng)模型不確定性和外界擾動(dòng)的綜合作用下,所設(shè)計(jì)的軌跡跟蹤控制器能夠?qū)θS軌跡進(jìn)行準(zhǔn)確、穩(wěn)定的跟蹤。