“玩轉”數學語言 解題不再困難

?首都師范大學教師教育學院

郭鑫培 閆瑞敏

1 引言

文字語言是數學問題最基本的表達形式，其特點是通俗，有助于理解題意，但有時敘述較為冗長、繁瑣.圖形語言的特點是直觀，便于觀察和聯想，但受制于學生的空間想象能力和圖形本身的復雜程度，有時難以理解.符號語言簡潔精煉，表述方便，有助于運算，但它的抽象性、概括性較強，對學生理解數學問題造成了一定的困難.三種數學語言各有所長，因此我們在解題時要善于靈活地轉換數學語言，高效解決問題.

2 數學語言之間的轉換

2.1文字語言向圖形語言、符號語言的轉換

文字語言轉換為圖形語言可以更加直觀地呈現數學問題，轉換為符號語言可以使數學問題量化、符號化，從而通過代數運算解決問題.

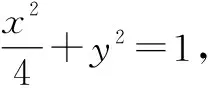
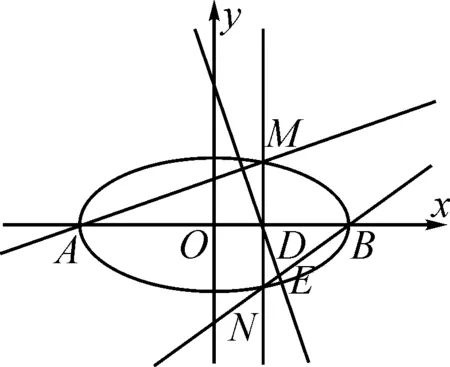
圖1

分析:首先我們通過文字語言理解題意，明確其中的幾何條件，然后將文字語言轉換為圖形語言，從而更加直觀地呈現問題，如圖1所示.再將其中的幾何條件轉換為符號語言，如斜率、垂直關系、相交關系等，最終要求證的是三角形面積之比，只需找到圖形中的有關三角形，利用三角形面積公式(符號語言)即可求證.

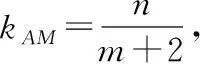
①

又直線BN的方程為

②

聯立方程①②，解得點E縱坐標為

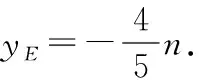
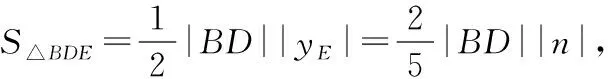
故△BDE與△BDN的面積之比為4∶5.

點評：解析幾何的核心思想是通過代數方法來解決幾何問題，但我們首先要做的是將題目中的文字語言轉換為圖形語言，即先將幾何問題呈現出來，否則后續的所有處理都是空談.

例2如圖2所示，北京天壇的圜丘壇分上、中、下三層，上層中心有一塊圓形石板(天心石)，環繞天心石砌9塊扇面形石板構成第一環，向外每環依次增加9塊，下一層的第一環比上一層的最后一環多9塊，向外每環依次也增加9塊，已知每層環數相同，且下層比中層多729塊，則三層共有扇面形石板(不含天心石) ( ).

圖2

A.3 699塊 B.3 474塊

C.3 402塊 D.3 309塊

分析：首先我們要對題目中的文字語言進行分析、轉換，借助示意圖理解題意，利用相應的數學模型解決問題.如果將上、中、下三層看作一個整體，仍滿足每一環比上一環多9塊，則這三層每一環石板數符合等差數列模型.再畫出示意圖理解各層石板數的關系，最后將“下層比中層多729塊”轉換為相應的符號語言進行求解即可.

圖3

解析：由題意可設每環中扇面形石板塊數構成的等差數列為{an},則a1=9,d=9.由每層環數相同，設每層有n環，每層之間石板數的關系如右圖3.

由下層比中層多729塊，結合示意圖轉換為符號語言，有(S3n-S2n)-(S2n-Sn)=729,即S3n-2S2n+Sn=729,利用等差數列前n項和公式，可得9n2=729，解得n=9.則三層共有扇面形石板S3n=3 402(塊).故選：C.

點評:面對文字量較大的題目，要仔細審題，從中提取關鍵信息，抓關鍵點；要善于畫示意圖來理解題意，同時檢索頭腦中相應的數學模型，從而實現數學語言之間的轉換.

2.2 圖形語言向文字語言、符號語言的轉換

圖形語言轉換為文字語言有助于對數學問題的理解與分析，轉換為符號語言有助于數學問題的解決，以“數”解“形”.

例3如圖4，牛牛從公園E處出發，先到F處與麗麗會合，再一起到位于G處的少年宮參加活動，那么牛牛到少年宮可以選擇的最短路徑有多少條[1]？

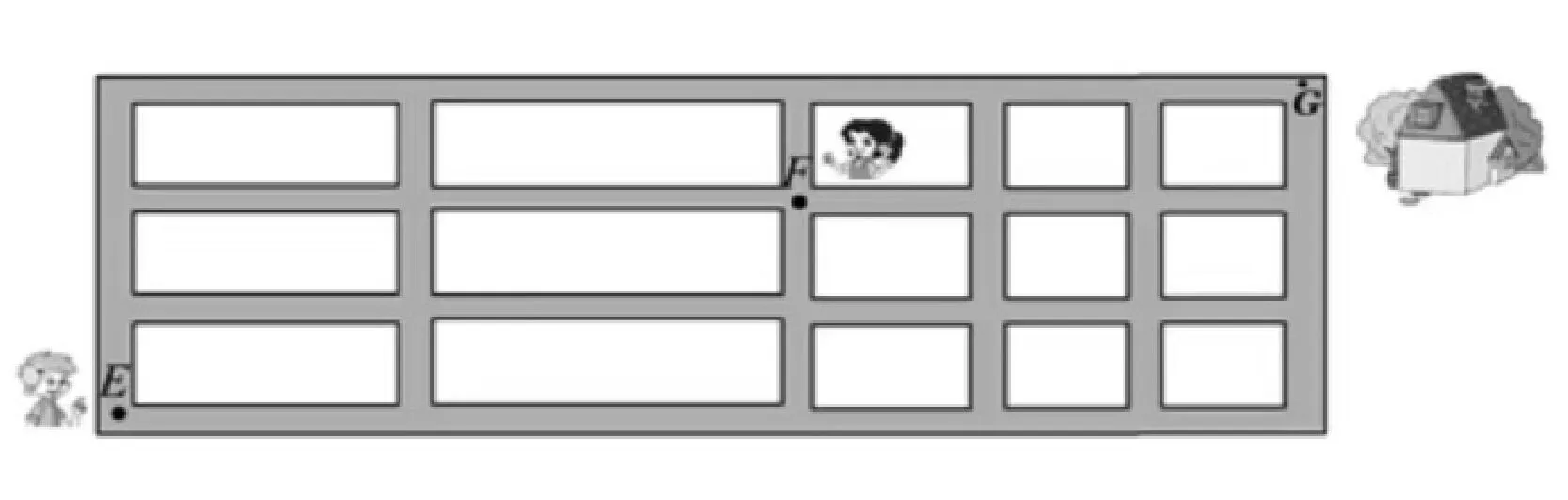
圖4

分析:本題是一個計數問題，要“完成的一件事”是從E處到G處，分兩步完成，即先從E處到F處，再從F處到G處，因此應利用分步乘法計數原理.我們先將其中的圖形語言轉換為文字語言，即將路線圖中的信息明確化，可以發現E到F處的最短路徑長度為以EF為對角線的矩形周長的一半，F到G處的最短路徑長度為以FG為對角線的矩形周長的一半，進而可以找出每一步的最短路徑條數，根據分步乘法計數原理計算公式(符號語言)求解即可.

解析：由題意可以知道第一步由E到F處共6條最短路徑，第二步由F到G處，共4條最短路徑.根據分步乘法計數原理，可知牛牛從E處到G處可以選擇的最短路徑條數共6×4=24.

例4：如圖5是一個獎杯的三視圖，試通過獎杯的三視圖計算它的體積和表面積.(尺寸如圖，單位：cm,π取3.14,結果取整數.)

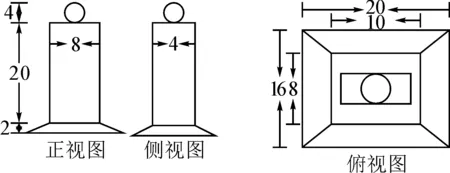
圖5

分析：本題是三視圖問題，信息全部蘊含在圖形之中，因此將圖形語言轉換為文字語言，是理解、分析問題的必要環節.觀察三視圖，可知該幾何體的上部是一個直徑為4 cm的球，中部是一個長、寬、高分別為8 cm，4 cm，20 cm的長方體，下部是一個棱臺，其中上底面是邊長分別為10 cm，8 cm的矩形，下底面是邊長分別為20 cm，16 cm的矩形，棱臺的高為2 cm.利用球、長方體、棱臺的體積公式(符號語言)即可求出體積.對于表面積，可以發現長方體和四棱臺有重合部分，因此計算表面積時，不要重復計算.

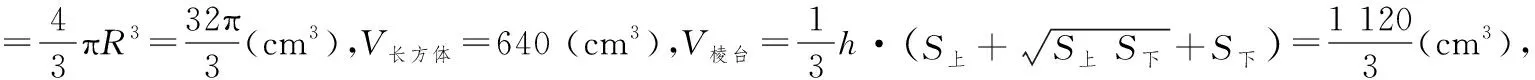
由球、矩形、梯形的面積公式，可得S球=4πR2=16π (cm2),通過計算可知，

點評：圖形語言向文字語言的轉換，是解決幾何圖形問題的第一步，但往往我們意識不到.這是因為在解題時，我們常常直接借助符號語言來定量計算，忽視了第一步轉換對理解問題的重要性.

2.3 符號語言向文字語言、圖形語言的轉換

符號語言轉換為文字語言可以使問題更加簡明，轉換為圖形語言可以使問題更加直觀、具體，以“形”助“數”.

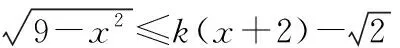
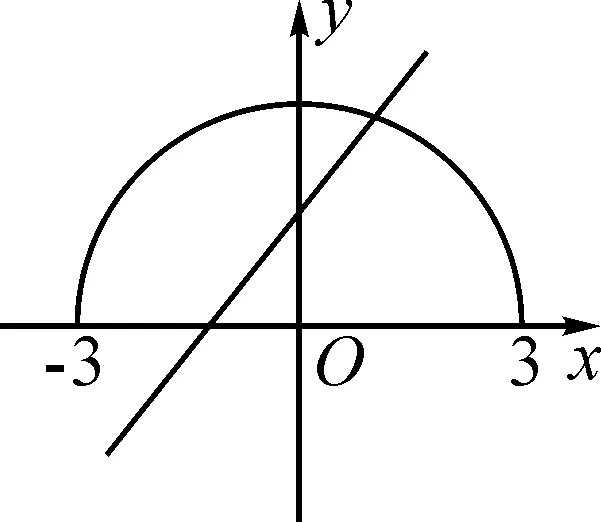
圖6

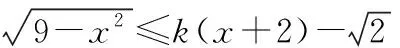
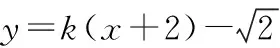
當k<0時，不滿足不等式的解集區間長度為2；

當k=0時，也不滿足題意.

因此，k>0.

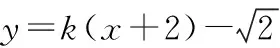
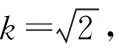
例6已知集合

A={(x,y)|y2=x+1,x,y∈R},

B={(x,y)|4x2+2x-2y+5=0,x,y∈R},

C={(x,y)|y=kx+b,x,y∈R},

是否存在正整數k和b使得(A∪B)∩C=??若存在，求出k和b的值；若不存在，請說明理由.

分析：先將題目中的符號語言轉換為文字語言，來理解題意.集合A和B所表示的都是拋物線，集合C表示一條直線，而(A∪B)∩C=?表示這條直線和兩條拋物線均不相交，還要注意k和b只取正整數.由此我們根據題意，將其中的符號語言轉換為圖形語言，如圖7所示.

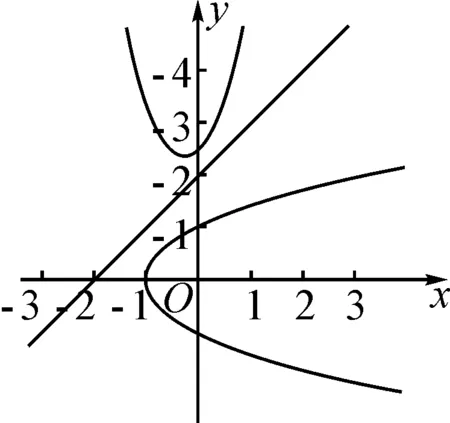
圖7

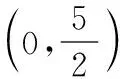
由b∈N*得b=2，則直線方程為y=kx+2.將直線方程分別和兩拋物線方程聯立，可得兩個方程組，

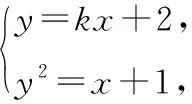
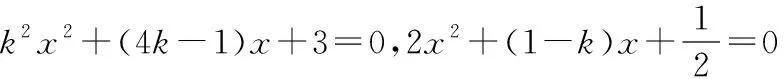
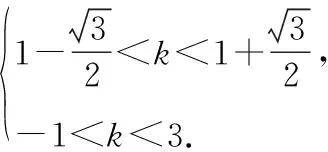
綜上所述，存在正整數k=1和b=2滿足題意.

3 總結

事實上，在解題的過程中，往往需要不止一次地進行數學語言之間的轉換，我們要知道每一次轉換都是為了更好地理解題目，從而有助于解決問題.因此在解題時，靈活地進行數學語言的轉換，可以大幅提高解題效率.這就需要我們在平時的學習中，深入理解與把握對“同一件事”的不同數學語言的表達形式，鍛煉數學語言轉換能力，“玩轉”數學語言，使解題不再困難.