考慮沙塵顆粒沖蝕損傷的航空葉片壽命預估

游文俊，梅威威，王計真，楊強，詹志新，胡偉平

1.北京航空航天大學，北京 100191

2.中國飛機強度研究所結構沖擊動力學航空科技重點實驗室，陜西 西安 710065

相比其他金屬材料，鈦合金具有比強度高、耐熱性好以及抗腐蝕性強等特點，廣泛運用于航空航天領域，在改善飛機結構設計并減輕飛機結構質量等方面起到了重要作用。鈦合金材料主要用于發動機葉片、機匣、燃燒室外殼及起落架等關鍵部位，其中，航空發動機的鈦合金葉片屬于轉動關鍵件，葉片表面易產生疲勞裂紋。在沙漠環境下，當航空發動機葉片和直升機槳葉在高速運行時，會吸入沙塵微粒等毫米級尺度的硬物，這些微粒撞擊在航空發動機葉片或其他部位，造成沖蝕損傷。一方面破壞了葉片的結構完整性，使得葉片易發生斷裂；另一方面葉片表面出現凹坑或缺口，導致葉片的局部應力集中并產生殘余應力，給發動機的疲勞性能或結構帶來不利影響，壽命急劇縮短，甚至是十分嚴重的后果。因此，研究沖蝕損傷對鈦合金葉片的疲勞影響，建立相應的評估方法，具有重要的應用意義，可為含沖蝕損傷葉片結構的疲勞損傷評定提供參考，有利于保障航空發動機葉片的正常運行，減少相應的飛行安全事故。

目前，針對結構的外物沖擊損傷問題，國內外的研究學者通過試驗手段和數值模擬取得了一定的成果。在試驗方面，Zhu 等[1]針對鋼球沖擊鈦合金平板，分析了不同沖擊角度下鈦合金平板的微觀形貌，研究了疲勞小裂紋的萌生和擴展行為。Duó 等[2]則測量了含沖擊損傷試樣的殘余應力分布，研究表明沖擊損傷的局部區域具有相對較高的應力梯度。Zabeen等[3]研究了外物損傷對激光噴丸處理構件的殘余應力場及裂紋擴展的影響。包珍強等[4]采用空氣炮沖擊試驗裝置，開展了鈦合金葉片的外物沖擊試驗，在不同的沖擊條件下分析了鈦合金的高周疲勞特性。黃偉等[5]基于空氣炮試驗裝置，開展了鈦合金沖擊損傷的宏觀和微觀分析，研究表明損傷局部有明顯的塑性變形。許祥勝等[6]對鈦合金平板試樣開展沖擊損傷試驗，發現沖擊損傷易于導致疲勞裂紋萌生,且對疲勞強度有較大影響。張宇等[7]基于二級空氣炮系統對V 形鋁合金靶板進行了高速沖擊試驗，發現其破壞模式為局部剪切沖塞，射彈角和射彈間距對塑性區大小有顯著影響。王計真[8]采用一種初始應力復合材料高速沖擊試驗方法，對復合材料層合板開展了高速沖擊試驗，研究發現面內初始應力對復合材料板高速沖擊行為影響顯著。在數值模擬方面，Mall 等[9]采用有限元方法計算模擬了外物沖擊損傷后的變形及應力狀態，并合理解釋了損傷和疲勞強度之間的關系。Oakley等[10]預測了燃氣輪鈦合金葉片在沖擊損傷后的剩余疲勞壽命，并開展相關試驗驗證了該方法的適用性。Lin 等[11]采用有限元方法分析了沖擊損傷后的激光沖擊噴丸的鈦合金試件的疲勞裂紋擴展行為，并計算了有效應力強度因子的范圍。張笑宇等[12]采用損傷力學方法對復合材料夾芯結構進行了冰雹沖擊和多次沖擊的數值分析，發現沖擊能量、位置和角度對損傷累積有明顯作用。

文獻研究表明，疲勞損傷的評估方法主要包括名義應力法[13]、局部應變法[14]、場強法[15]、臨界平面法[16]和損傷力學方法[17]等，這些方法各有利弊。其中，損傷力學方法通過引入損傷變量，來研究結構或材料的力學性能在循環載荷作用下的劣化規律[18-19]，其優點是物理意義比較明確。研究表明，相比常規結構，含沖蝕損傷的結構疲勞特性預估要復雜得多[20]，必須考慮沖蝕損傷對結構疲勞性能的影響。這一影響主要表現在沖蝕造成結構局部的殘余應力應變場和沖蝕造成結構表面沖蝕坑缺陷后在受載過程中引起結構局部區域的應力集中。

本文基于連續損傷力學理論，建立考慮沙塵顆粒沖蝕損傷鈦合金葉片疲勞壽命的預測方法。首先，采用有限元顯式分析，模擬真實的沖蝕過程，得到沖蝕后局部區域的初始缺陷；其次，基于疲勞損傷模型，建立損傷力學數值解法；最后，對含沖蝕損傷的鈦合金葉片進行了壽命預估，并分析了不同沖蝕條件對其疲勞損傷及壽命的影響。

1 理論模型

1.1 損傷耦合的彈塑性本構模型

在連續損傷力學理論中，以代表性體積單元（RVE）為研究對象，在RVE中某一方向的截面面積為S，總的微觀缺陷面積為Sd，則損傷度D[21]定義為總微觀缺陷面積與截面面積之比，即

當材料處于無損狀態時，Sd= 0，即D= 0；當Sd=S時，疲勞裂紋萌生。RVE的有效承載面積SR定義為

在外載荷P作用下，有效應力σ?為

基于應變等效假設，受損材料的彈性模量Ed定義為

式中：E為無損時的彈性模量。

本文采用的彈塑性本構模型，可以考慮各向同性以及隨動硬化。對于小變形而言，總應變εij可以表示為εii=+，其中，為彈性應變和為塑性應變。根據有效應力概念和應變等效假設，耦合損傷的本構方程如下

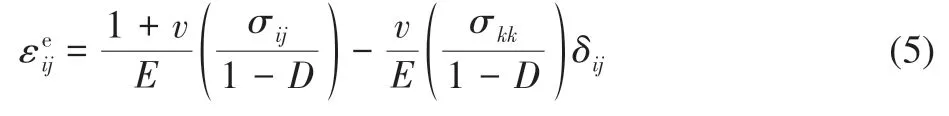
此外，損傷耦合的屈服準則F為

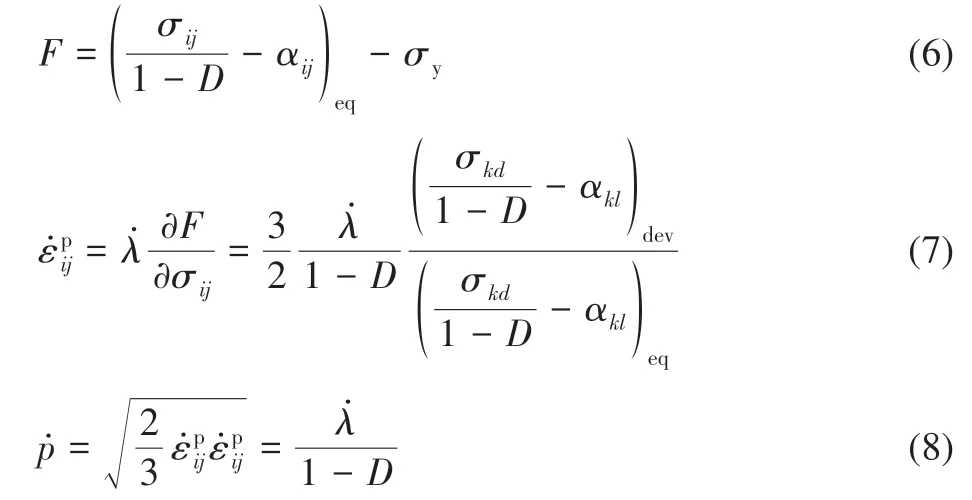
式中：括號的下標“eq”和“dev”分別代表的是Von Mises 等效應力和應力的偏量部分；αij為背應力；σy為屈服極限；λ?為塑性乘子；p?為累積塑性應變率。非線性隨動硬化律如下

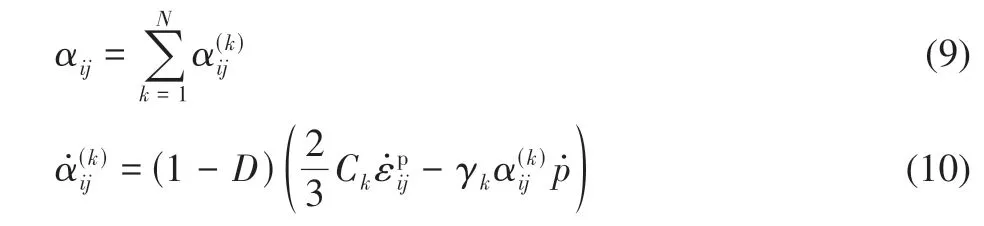
式中：N為背應力分量的個數；Ck和γk是由試驗結果決定的材料參數。

1.2 疲勞損傷演化模型

Chaboche等[22]損傷演化模型是一種常用的能夠反映非線性損傷累積現象的模型。Chaudonneret[23]對單軸疲勞損傷模型進行了分析，提出了多軸疲勞損傷演化方程

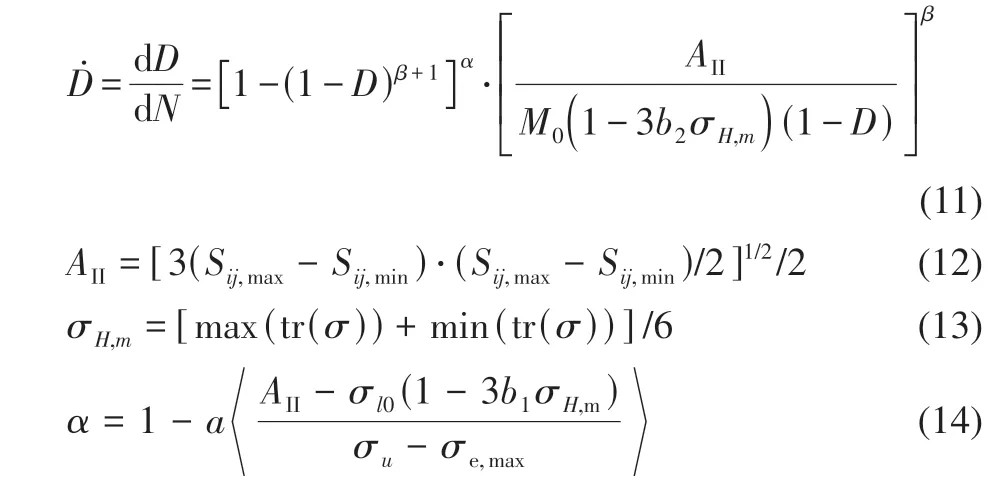
以上表達式中包含a、M0、β、b1和b2這5 個材料參數。AII為八面體切應力幅值；Sij,max和Sij,min分別為一個載荷循環歷程中偏應力分量的最大和最小值；σH,m是一次循環靜水壓力的平均值；σe,max是一個載荷循環內的最大等效應力。對多軸損傷演化方程從初始損傷下限積分到上限，可得材料破壞時的疲勞壽命NF為

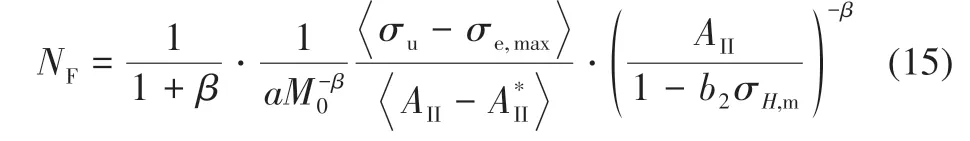
在單軸加載下，考慮由于沖蝕引起的初始損傷De的疲勞損傷演化方程的表達式為

式中：σu為強度應力；σmax為最大應力；σa為應力幅值；σm為平均應力；σf為疲勞極限。在實際應用過程中，危險部位的應力狀態是復雜的，多軸情況下考慮由沖蝕引起的初始損傷De的疲勞損傷演化方程的表達式為

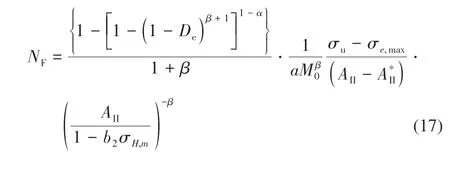
2 數值計算方法與材料參數標定

2.1 計算方法

在本節中，基于前述損傷耦合的彈塑性本構模型和疲勞損傷演化模型，建立損傷力學-有限元數值計算方法，以計算考慮沙塵顆粒沖蝕損傷的葉片的疲勞壽命。本研究所涉及的數值計算方法是在ABAQUS 平臺上通過二次開發實現的。具體的計算過程如下：（1）初始化模型中所有的參數，編寫彈塑性本構模型的VUMAT 子程序進行沖蝕過程模擬，得到沙塵顆粒沖蝕后葉片局部的殘余應力場和塑性應變場；（2）結合沖蝕過程的動力學模擬，得到不同的沖擊速度和沖擊角度下造成的初始缺陷的尺寸和形狀；（3）建立疲勞損傷計算的有限元模型，并初始化模型中所有的參數；（4）采用ABAQUS 軟件，并結合編寫的耦合損傷的彈塑性本構模型和疲勞損傷模型的VUMAT子程序計算含沖蝕損傷的應力應變場，以及每個單元高斯積分點的損傷速率和損傷度；（5）如果任意一個單元的損傷度累積達到了1，則認為疲勞裂紋在這個單元萌生，此時的循環次數即為疲勞裂紋的萌生壽命，如果沒有達到1，重復步驟（4），直至損傷度達到1。

2.2 材料參數的標定

根據Ti6Al4V 鈦合金板的靜力拉伸試驗[24]，得到其基本的彈塑性本構參數，見表1。然后，根據標準光滑試驗件的高周疲勞試驗[24]，標定多軸疲勞損傷模型中的損傷演化參數。其中，β,b1,b2可以直接根據對稱循環疲勞試驗和一個非對稱循環疲勞試驗得出，最后再采用損傷力學有限單元方法和一組缺口件疲勞試驗參數，可以對獨立的參數a和M0進行標定[25]。標定的所有參數在表2中列出。采用標定參數計算出的疲勞壽命與試驗數據的誤差在表3 中列出。由此可以看出，標定的參數可以滿足計算精度的要求。

表1 材料的靜力力學性能參數Table 1 Static mechanical properties of material

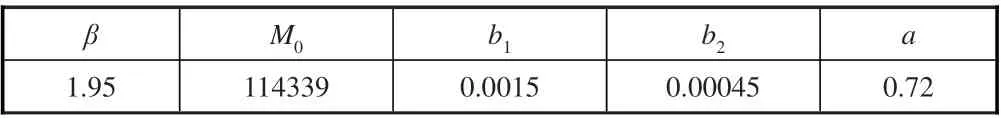
表2 材料的疲勞性能參數［25］Table 2 Fatigue properties of material

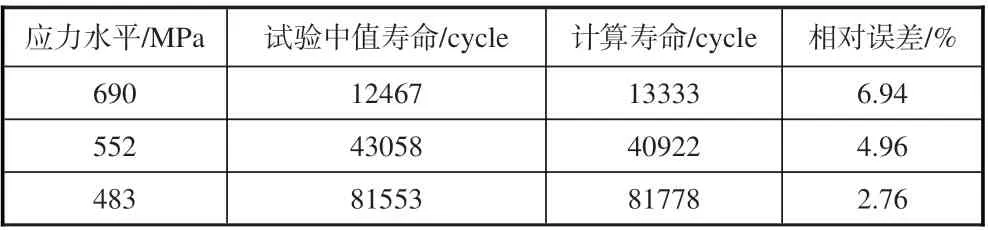
表3 計算的疲勞壽命與試驗數據的對比Table 3 Comparison between the computed fatigue lives and experimental results

3 沖蝕力學響應分析

在ABAQUS 中建立沖蝕過程有限元模擬模型。利用該模型分別進行三種不同沖擊速度（50m/s、100m/s、150m/s）、三種不同沖擊角度（0°、60°、30°）的沖蝕過程模擬，分析沖蝕的力學響應。沖蝕示意圖如圖1所示。

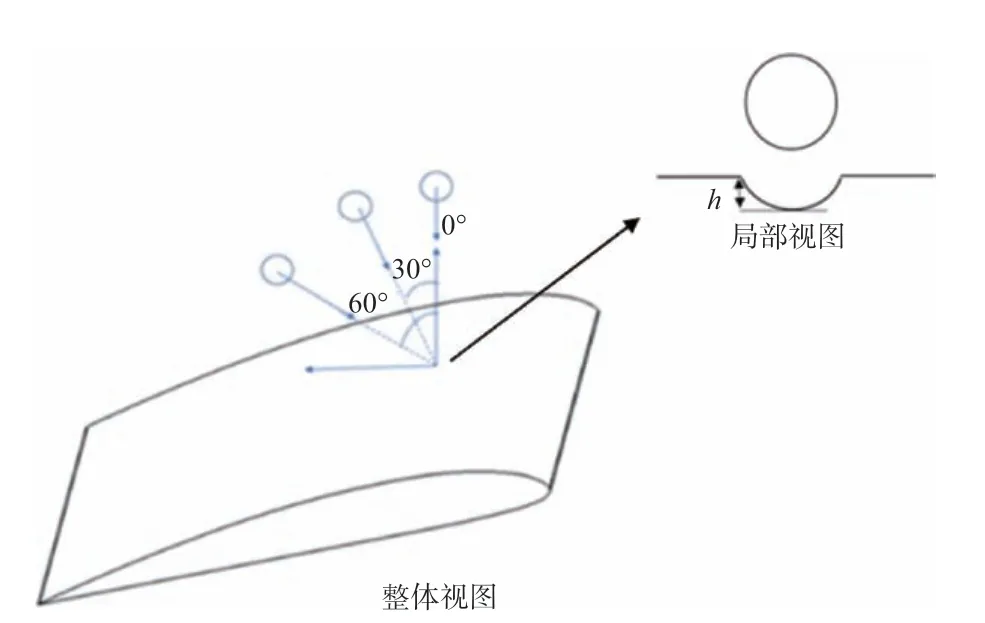
圖1 沖蝕示意圖Fig.1 Impact diagram

3.1 沖蝕有限元模型

沖蝕有限元模型如圖2 所示。在ABAQUS 平臺上，考慮到葉片模型的復雜性，建立葉片全模型，在端面上施加固支邊界條件。考慮到葉片整體外形曲面形狀，采用C3D4實體單元來進行網格劃分，因為四面體網格能較好地適應復雜形狀。整個有限元模型如圖2 所示，一共有236370 個單元、338874個節點；對葉片沖擊接觸部位網格進行細化，最小網格尺寸為0.1mm；球形沖擊物有限模型如圖2 所示。此外，還需對網格的密度無關性進行驗證，確保在此密度下的網格可以保證和滿足數值計算的精度。

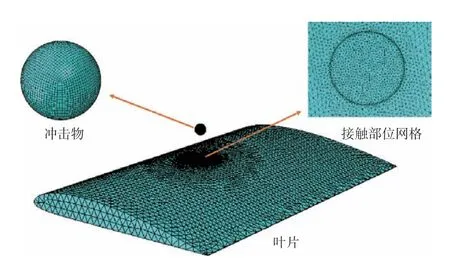
圖2 沖蝕有限元模型Fig.2 Finite element model

3.2 沖蝕凹坑分析

采用3.1節中的有限元模型開展沖擊過程模擬，得到葉片的沖蝕缺陷特征，如圖3所示。這里，利用該模型進行了三種速度v（50m/s, 100m/s, 150m/s）、三種角度α（0°，30°，60°）共9種情況的沖擊過程模擬，9種不同情況的模擬結果見表4（h表示沖蝕坑的深度）。

圖3 含沖蝕坑葉片的有限元模型圖Fig.3 Finite element model of the blade with impact pit

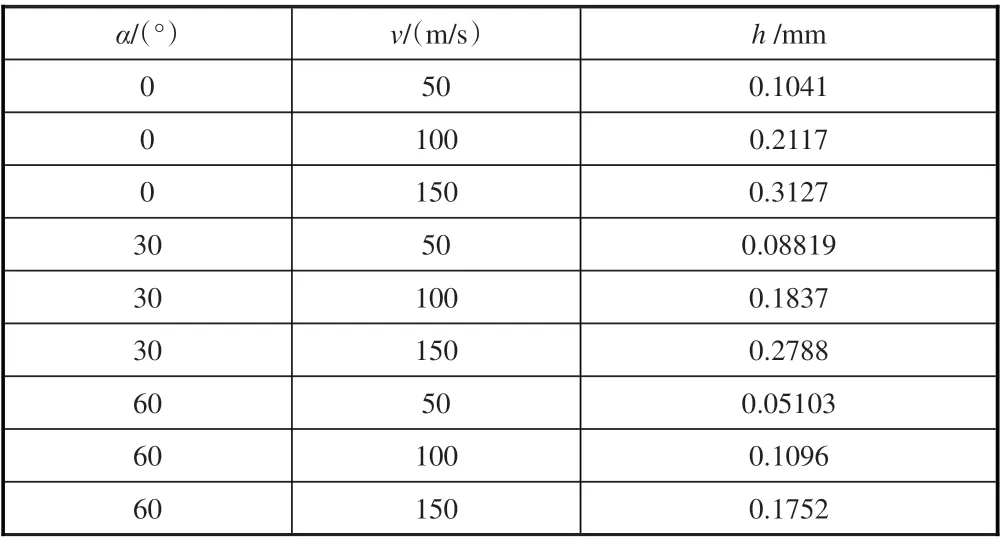
表4 沖擊模擬工況Table 4 Impact simulation cases

圖4為沖蝕坑深度隨沖擊角度和速度的變化情況。由圖4可以看出，當沖擊角度一定時，隨著沖擊速度增大沖擊凹坑越深；沖擊速度一定時，隨著沖擊角度增大沖蝕坑深度越小。

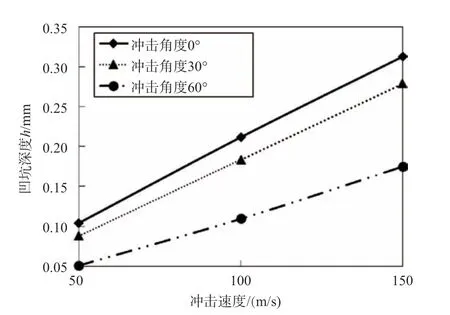
圖4 沖蝕坑深度隨沖擊角度和速度的變化Fig.4 Variation of impact pit depth with impact angle and velocity

3.3 沖蝕殘余應力、應變及塑性損傷分析

葉片受到外物沖擊后，沖擊能量被葉片吸收一部分以塑性變形能的形式耗散，產生塑性變形，從而在受沖擊區域產生較大的殘余應力。由于循環加載時沿葉片長度方向（也即Z軸方向）加載，故葉片加載方向的殘余應力對疲勞壽命的影響起到主導作用，本文稱之為軸向殘余應力。沖擊損傷部位附近的軸向殘余應力分布如圖5所示。沖擊損傷部位附近的殘余應變如圖6所示。軸向殘余應力沿沖蝕坑深度方向的變化規律如圖7所示。由圖7可以看出，沖擊速度越大軸向殘余應力越大，軸向殘余應力先隨深度方向增大而增大，而后隨深度方向增大而減小。由于塑性變形無法恢復，因此會產生殘余應變。

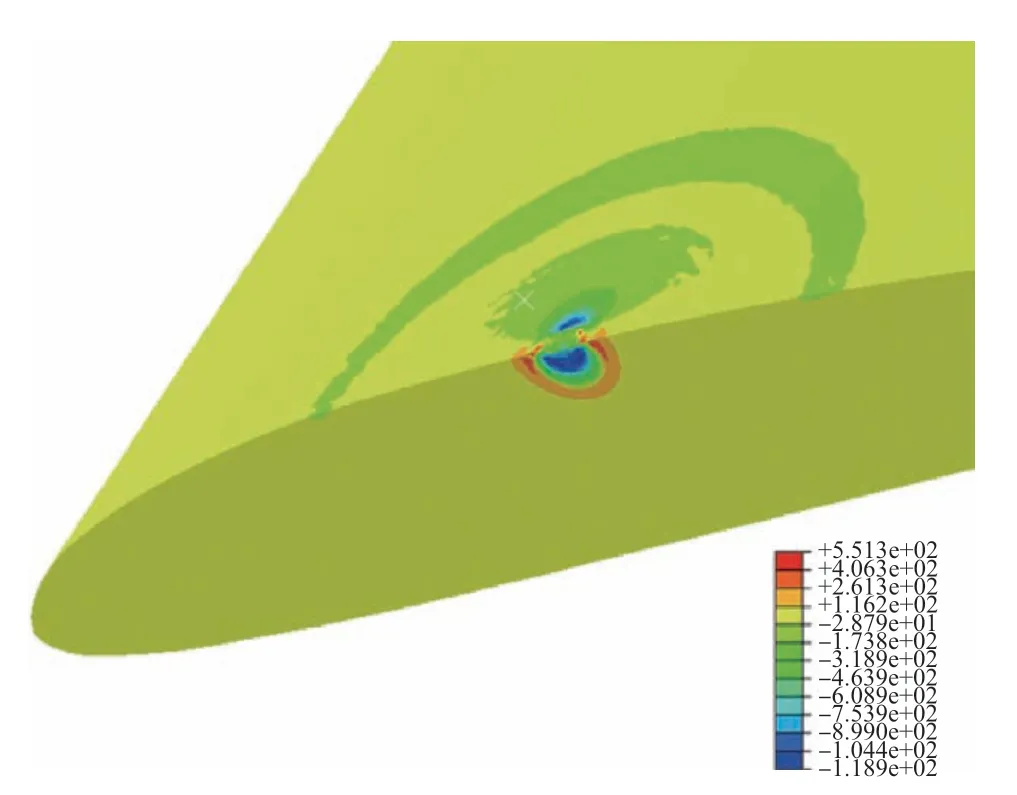
圖5 軸向殘余應力分布圖Fig.5 Distribution of axial residual stress

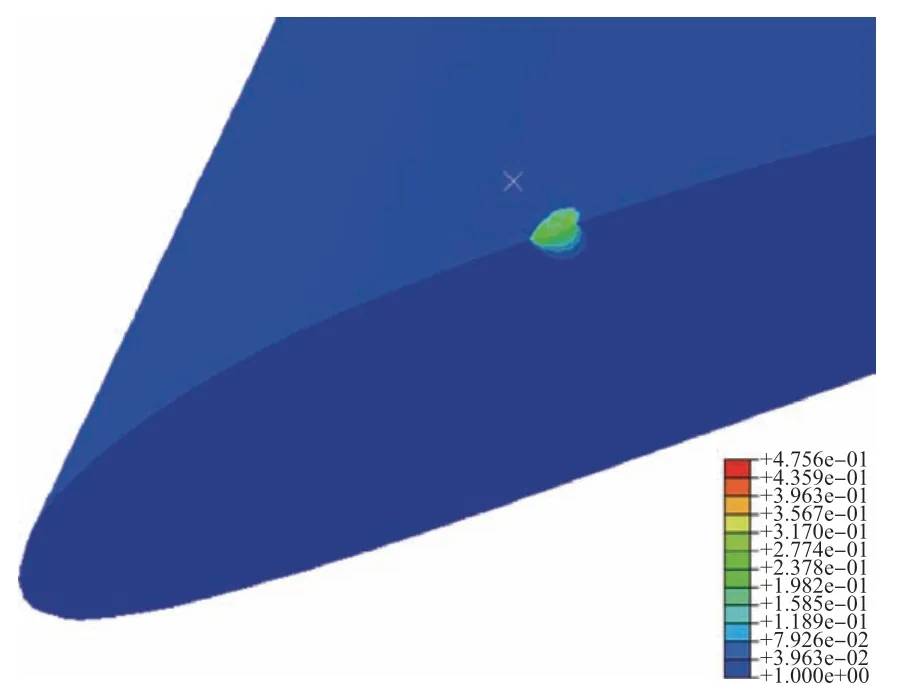
圖6 殘余應變分布圖Fig.6 Distribution of residual strain

圖7 軸向殘余應力沿沖蝕坑深度方向變化趨勢Fig.7 Variation trend of axial residual stress along pit depth

由沖擊過程產生的塑性變形所導致的沖擊損傷可以歸類為延性損傷。圖8 展示了受沖擊部位的塑性損傷分布，從圖8中可看出，沖蝕坑底部的沖擊損傷最大。

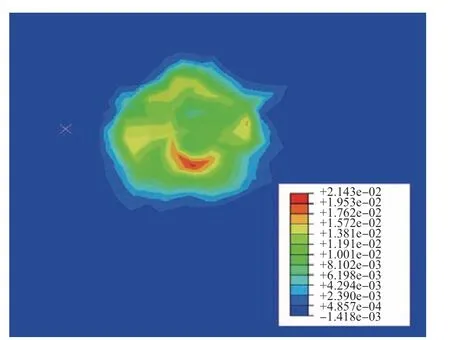
圖8 塑性損傷分布圖Fig.8 Distribution of plastic damage

圖9 給出了不同沖擊角度下軸向殘余應力隨沖擊速度的變化而變化的規律。從圖9 中可以看出，沖擊速度越大殘余壓應力越大。圖10 給出了不同沖擊速度下軸向殘余應力隨沖擊角度變化而變化的規律，從圖10中可以看出沖擊角度越大軸向殘余壓應力越大。

圖9 殘余應力隨不同沖擊角度速度的變化Fig.9 Variation of residual stresses with different impact angles

圖10 殘余應力隨不同沖擊速度的變化Fig.10 Variation of residual stresses with different impact speeds

圖11、圖12給出了不同沖擊角度、不同沖擊速度下的殘余應變變化規律。由圖11 可以看出，當沖擊角度一定時，沖擊速度越大則殘余應變越大。沖擊速度越大則動能越大，當外物與葉片接觸時會有更多的能量轉化為塑性變形能，因此殘余應變會更大。由圖12可以看出，沖擊速度為150m/s，沖擊角度為60°時，殘余應變最大為0.929。

圖11 殘余應變隨沖擊角度的變化Fig.11 Variation of residual strain with impact angles

圖12 殘余應變隨沖擊速度的變化Fig.12 Variation of residual strain with impact speeds

由圖13 可以看出，當角度一定時，沖擊速度為100m/s時沖擊損傷最小。由圖14可以看出，在沖擊速度為150m/s、沖擊角度為60°時，造成的塑性損傷最大為0.148。這可能與葉片的曲面形狀有關。本文中的60°沖擊角度可能比葉片曲面上受沖擊點的法線夾角更小，從而使更多的動能轉化為塑性變形能，導致更大的塑性損傷。

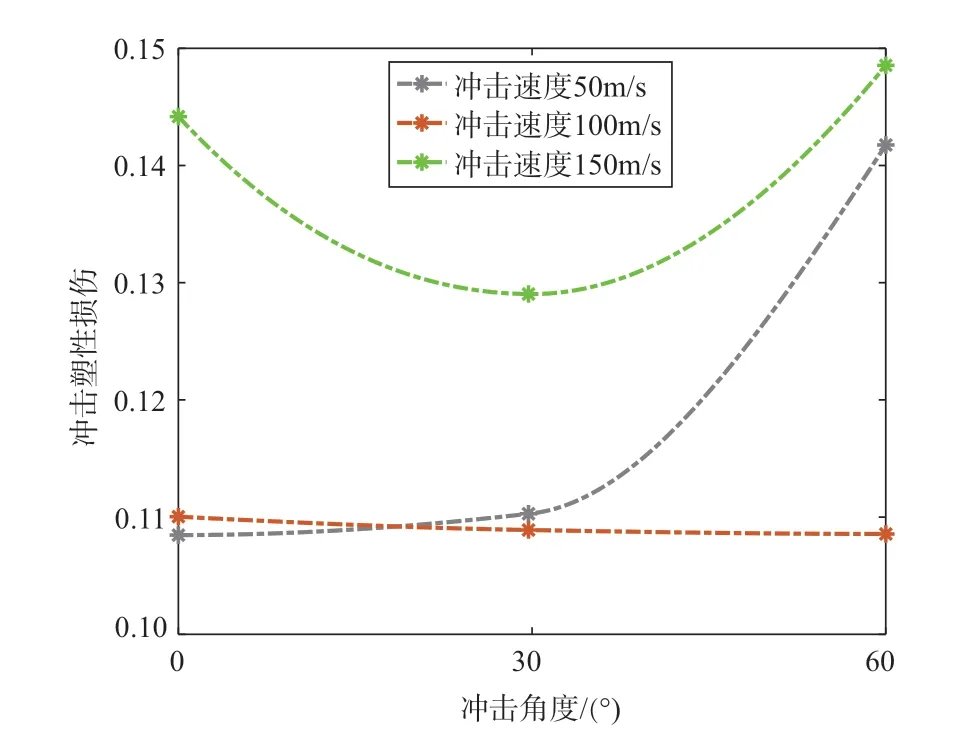
圖13 沖擊塑性損傷隨沖擊角度的變化Fig.13 Variation of impact plastic damage with impact angles

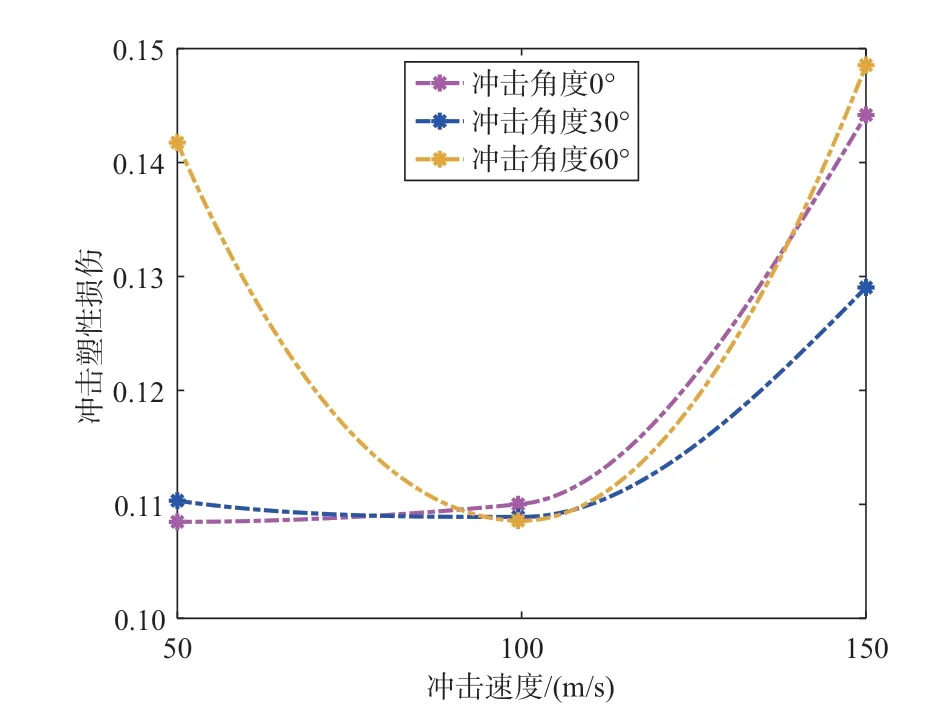
圖14 沖擊塑性損傷隨沖擊速度的變化Fig.14 Variation of impact plastic damage with impact speeds

4 含沖蝕凹坑的鈦合金葉片的疲勞壽命計算

沖蝕后產生不同的缺口形狀和不同殘余應力，會對葉片的疲勞壽命造成顯著影響。本節計算的壽命曲線考慮了以下三個方面的影響：（1）沖蝕損傷所造成的葉片沖蝕坑局部的應力集中；（2）由殘余應力和塑性應變造成的初始沖蝕損傷；（3）循環載荷所導致的疲勞損傷。本節基于損傷力學-有限元數值方法，對于不同沖擊速度和角度情況，計算了三級應力水平下含沖蝕損傷鈦合金葉片的疲勞壽命，進而繪制了不同沖擊速度和角度下的載荷—壽命曲線。在不同的沖擊速度下，載荷應力比為0.1，圖15～圖17 給出了計算得到的葉片疲勞壽命，這里分別給出了三種沖擊角度的預測壽命。可以發現，當沖擊角度一定、沖擊速度不同時，葉片的疲勞壽命變化規律一致，即隨著沖擊速度的增大，鈦合金材料的葉片疲勞壽命在不斷減小。對于最大名義應力為611MPa的情況，在三種不同的沖擊速度下，損傷度隨著循環次數的變化趨勢如圖18 所示。沖擊速度由50m/s、100m/s、150m/s 依次變化，損傷速率在不斷增加；從單個損傷度隨循環次數變化來看，隨著循環次數增加，損傷速率在不斷增加，且損傷速率在最后階段增速明顯。可見，沖擊速度是影響受沖擊葉片疲勞壽命的重要因素。

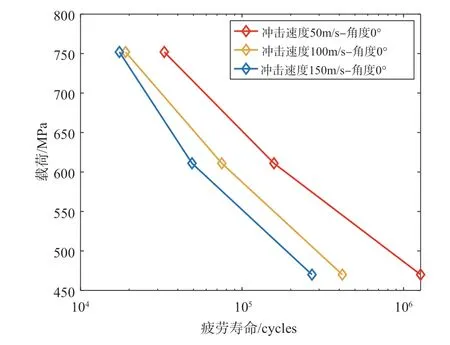
圖15 沖擊角度為0°時，不同沖擊速度下預估的疲勞壽命Fig.15 Predicted fatigue life under different impact velocity at the impact angle of 0°

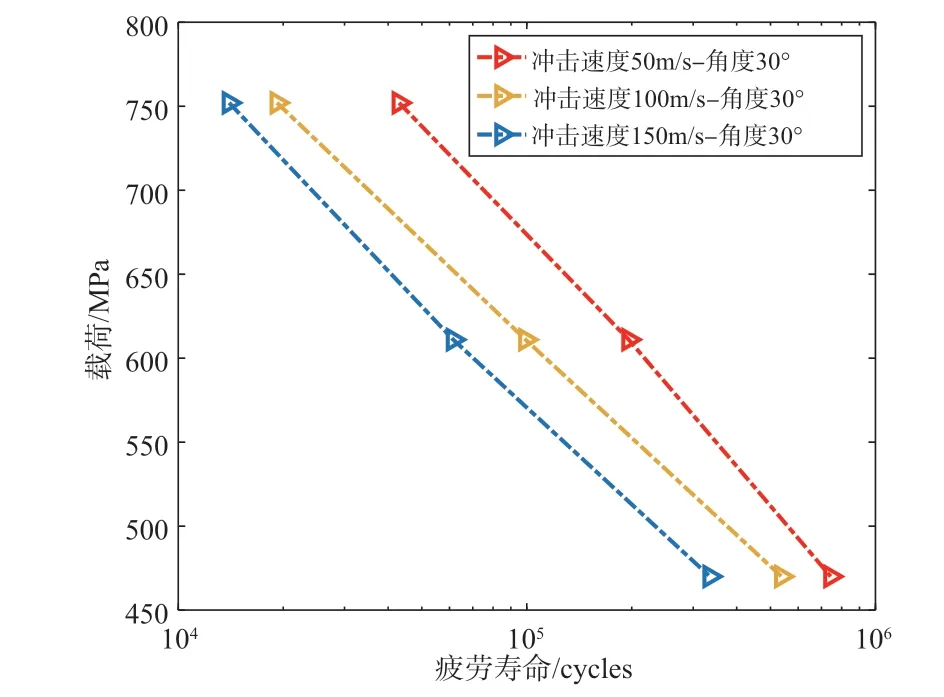
圖16 沖擊角度為30°時，不同沖擊速度下預估的疲勞壽命Fig.16 Predicted fatigue life under different impact velocity at the impact angle of 30°

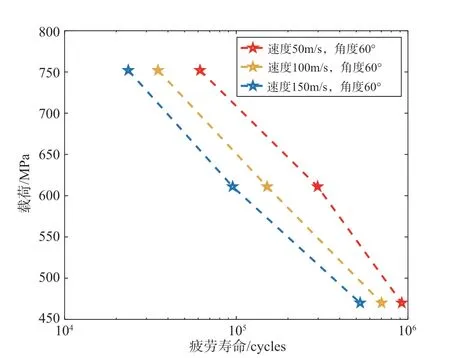
圖17 沖擊角度為60°時,不同沖擊速度下預估的疲勞壽命Fig.17 Predicted fatigue life under different impact velocity at the impact angle of 60°

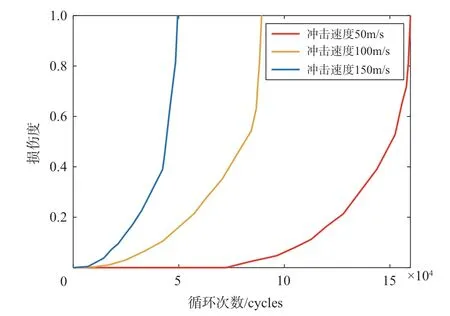
圖18 不同的沖擊速度下，損傷度隨著循環次數的變化趨勢Fig.18 Change trend of damage degree with the number of cycles under different impact speed

在不同的沖擊角度下，載荷應力比為0.1，圖19～圖21給出了計算得到的葉片的疲勞壽命，這里分別給出了三種沖擊速度的預測壽命。可以發現，當沖擊速度一定、沖擊角度不同時，葉片的疲勞壽命變化規律一致，即隨著沖擊角度的增大，鈦合金材料的葉片疲勞壽命在不斷增加。對于最大名義應力為611MPa的情況，在三種不同的沖擊角度下，損傷度隨著循環次數的變化趨勢如圖22所示。可以看到，沖擊角度從0°、30°再到60°依次變化，損傷速率依次降低；從單個損傷度隨循環次數變化來看，隨著循環次數增加，損傷速率在不斷增加，且損傷速率在最后階段增速明顯。可見沖擊角度也是影響受沖擊葉片疲勞壽命的重要因素之一。

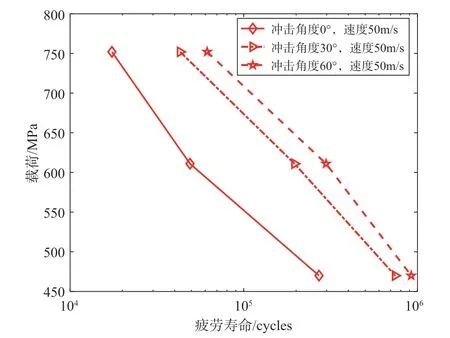
圖19 當沖擊速度為50m/s時，不同沖擊角度下預估的疲勞壽命Fig.19 Predicted fatigue life under different impact angle at the impact velocity of 50m/s

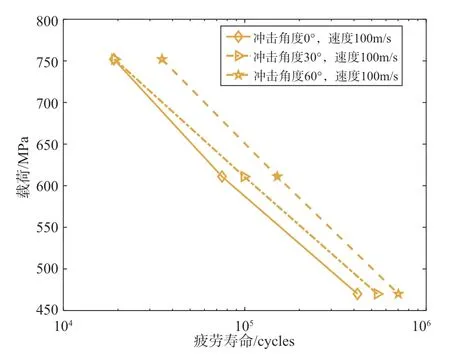
圖20 當沖擊速度為100m/s時，不同沖擊角度下預估的疲勞壽命Fig.20 Predicted fatigue life under different impact angle at the impact velocity of 100m/s

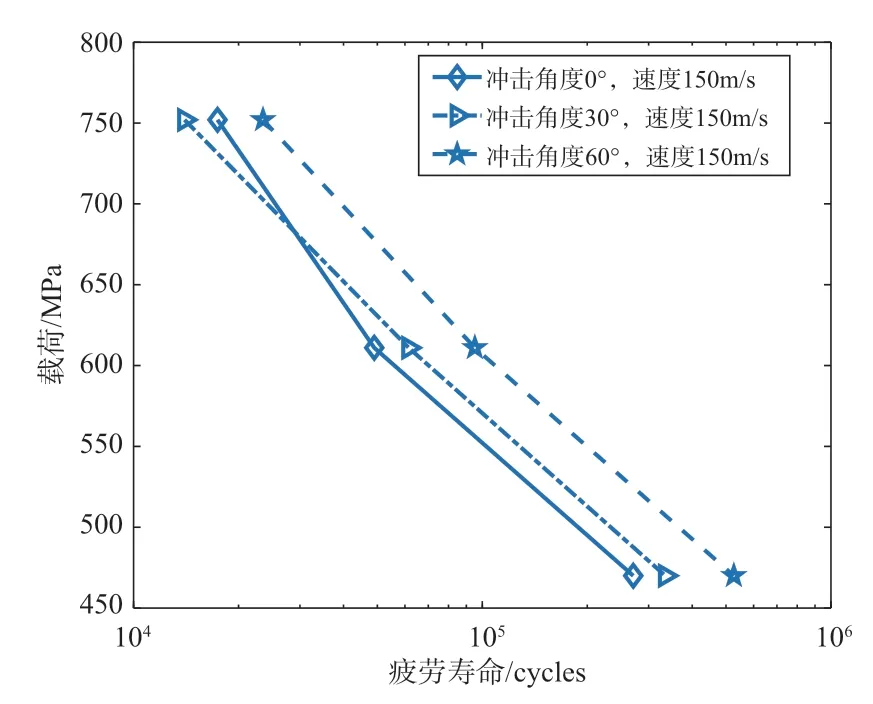
圖21 當沖擊速度為150m/s時，不同沖擊角度下預估的疲勞壽命Fig.21 Predicted fatigue life under different impact angle at the impact velocity of 150m/s

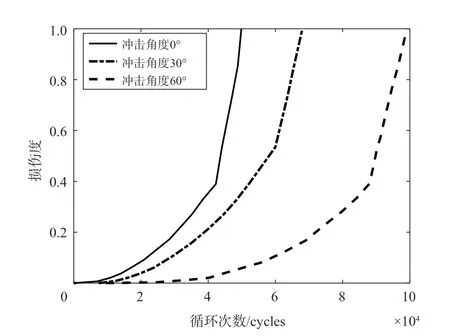
圖22 不同的沖擊角度下,損傷度隨著循環次數的變化趨勢Fig.22 Change trend of damage degree with the number of cycles under different impact angles

5 結論

本文建立了基于損傷力學的考慮沙塵顆粒沖蝕損傷鈦合金的疲勞壽命分析方法，并以鈦合金葉片為例進行了沖蝕疲勞損傷分析及壽命預測，主要結論如下。

（1）基于有限元顯式計算，通過編寫彈塑性本構模型的VUMAT，模擬了沙塵顆粒沖擊鈦合金葉片的過程，分析了沖擊葉片產生的力學響應，包括沖蝕坑、殘余應力、殘余應變以及初始塑性損傷。

（2）基于損傷力學理論，推導了疲勞損傷模型，通過編寫VUMAT，實現了損傷力學數值算法，以計算考慮沖蝕損傷的應力應變場；并預估了含沖蝕損傷的鈦合金葉片的疲勞壽命。

（3）開展了受沖蝕損傷后葉片的疲勞壽命影響因素分析，不同沖擊速度和沖擊角度會造成特征不同的沖擊缺陷，進而引起葉片的局部應力集中，最終影響葉片的疲勞損傷累積。