用于飛機模型參數辨識的飛行數據處理方法研究

葉子豪，張曉敏，劉亞飛，董朝陽

1.北京航空航天大學，北京 100191

2.中國飛行試驗研究院航空工業飛行仿真航空科技重點實驗室，陜西 西安 710089

隨著航空技術的不斷進步，機載傳感器的數量大量增加，機載傳感器所收集、交換的數據量成倍增長，飛行過程中產生的飛行器監測數據規模也隨之不斷增大。上述監測數據中包含了飛行器的全部狀態量、控制量以及飛行軌跡等信息，能夠充分體現當前飛行器控制系統設計的優劣，對控制系統的設計優化與飛行器性能的優化有著重要的指導意義。但現代飛行器的工作環境的復雜性與多變性將導致傳感器采集到的數據中包含較多的異常數據，其中的野值、隨機誤差、零位誤差、比例誤差與時間延遲[1-2]是影響數據質量的重要因素，將對后續研究的過程與結果產生直接影響。

現有的多路傳感器數據處理方法主要面向電氣工程與雷達網絡，面向飛行數據的誤差辨識與補償方法的研究較少，且存在過程不連貫、進行大規模數據處理時效率較低與通用性較差的缺點，難以滿足飛行器監測數據的大規模特性的要求，在飛行數據的批量與快速處理上存在著較大不足，難以滿足以飛行器控制系統的評估、設計與優化為目的的飛行器模型參數辨識以及后續多傳感器信息[3]融合的需求。

關于以數據中時間延遲的辨識與補償為代表的飛行數據處理方法，許多學者展開了研究。羅藝[4]等提出了基于極大似然法的異類傳感器數據配準方法。Zhang Pixu等[5]基于最小二乘法提出了多平臺傳感器系統誤差的配準算法。蔡金獅等[1]構建了考慮誤差的飛行數據數學模型，并系統地總結了飛行數據相容性檢驗的基本方法。劉超等[6]利用同一來源的數據中不同測量量間的微積分關系對不同測量量間的時間延遲進行了計算與修正。同時結合基于真實試飛數據的氣動導數辨識，驗證了該方法的有效性。王偉[7]基于拉格朗日插值法和卡爾曼濾波法提出了一種改進型的數據時間配準方法。李富剛等[8]基于增廣卡爾曼濾波法與輸出誤差法提出了一種新的飛行數據相容性檢驗方法。Panuntun等[9]提出了基于Smith預測器對四旋翼飛行器控制系統中的時間延遲的補償方法，并結合仿真結果得出了該方法在跟蹤性與抗干擾性方面的優勢。唐思圓[10]等采用了遺傳算法計算多傳感器系統誤差配準問題的解，并結合雷達真實數據與仿真數據驗證了該方法的有效性。在基于飛行數據處理的飛行器模型參數辨識方面，段偉偉[11]等分析了神經網絡、遺傳算法在控制系統參數辨識與建模上的應用。

首先，本文基于縱向小擾動線性模型構建了離散化數據相容性檢驗模型,并使用該模型生成含異常數據的模擬飛行數據。其次，對數據中的野值展開了識別-剔除與補正，并基于Savitzky-Golay 法進行了數據的平滑濾波。再次,基于極大似然法設計了數據中時間延遲、零位與比例誤差的辨識與補償方法。結合應用實例表明，控制量數據的常值誤差辨識與補償顯著改善了飛機模型參數辨識的迭代過程與結果的精度。最后，本文基于上述內容對結合常值誤差補償的飛行器模型參數辨識組合方法及其在飛行器設計中的應用進行了設計。

1 用于模型參數辨識的飛行數據處理方法

1.1 飛行數據相容性檢驗主要內容和方法

飛行器動力學系統試驗的測量數據常含有零位誤差或時間延遲等常值誤差造成各實測數據互不協調，即各狀態參數不滿足運動方程組[1]。飛行數據不相容將對包括飛機模型參數辨識在內的后續數據挖掘與研究工作造成不利影響。本文結合飛行器縱向小擾動線性模型，對飛行數據進行相容性檢驗。飛行數據相容性檢驗的基本思路是，以飛行器動力學方程組作為狀態方程，將常值誤差與比例誤差作為待估計參數，通過系統辨識方法估計出實測數據中的常值誤差與比例誤差并加以補償，即可得到相容的飛行數據[1]。只有當某觀測量既可以通過直接測量，又可以由其他觀測量通過運動關系式求出時，即該觀測量有多余的測量時，數據相容性檢驗才能夠進行。用于估計零位誤差、時間延遲與比例誤差的飛行數據數學模型為

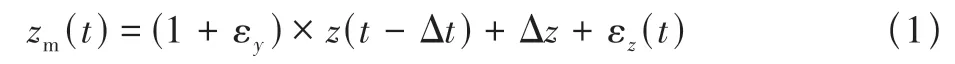
式中：zm為飛行數據實測值；z為飛行數據理想測量值；Δt為時間延遲；εy為比例誤差；Δz和εz是由傳感器的零位漂移及工作不穩定而引入的零位誤差與隨機誤差，隨機誤差εz為白噪聲，其均值為0，其方差為R。飛行數據實際值的表達式為

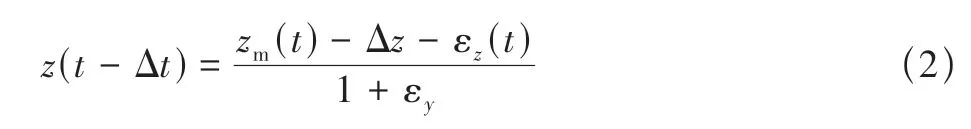
本文選用縱向小擾動線性模型作為狀態方程，其矩陣形式為

狀態變量x=[ΔV，Δα，Δq，Δθ]T，其中ΔV為速度變化值，Δα為迎角變化值，Δq為俯仰角速度，Δθ為俯仰角變化值。控制變量u=[Δδe，Δδp]T，其中Δδe為升降舵偏角，Δδp為油門大小變化。

系統矩陣A與控制矩陣B內的各項參數為在實際工程應用中為需要通過辨識得到的飛行器模型參數，通常為常數。縱向輸出方程為y=Cx+Du，其中C為四階單位矩陣，D為零矩陣。

結合飛行數據相容性檢驗的基本方程與選用的狀態方程，建立含有零位誤差、時間延遲、比例誤差與隨機誤差的飛行數據相容性檢驗模型。其狀態方程為

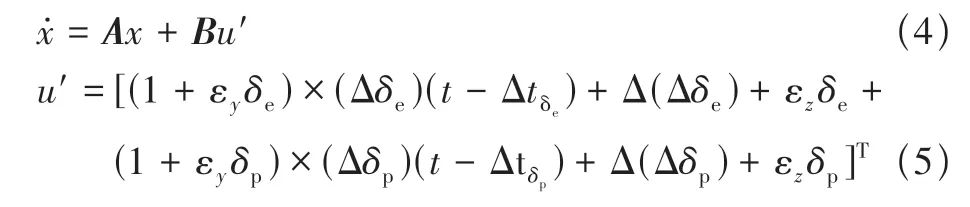
式中：[(Δδe)(t-Δtδe), (Δδp)(t-Δtδp)]為含時間延遲[Δtδe, Δtδp]（以狀態量的時間坐標為基準坐標）的控制量測量值；[Δ(Δδe)，Δ(Δδp)]、[εzδe，εzδp]與[εyδe，εyδp]分別為控制量的零位誤差、隨機誤差與比例誤差。觀測方程為

其中，xt=[ΔVt,Δαt,Δqt,Δθt],εzy=[εV,εα,εq,εθ]，分別為狀態量的測量值和隨機誤差。待估計的常值誤差與比例誤差為

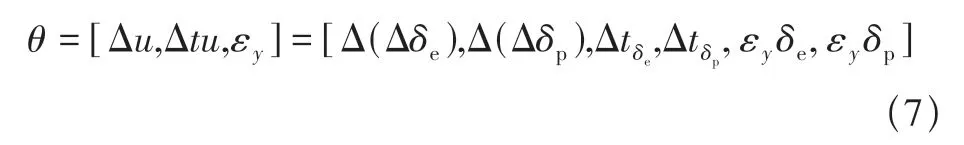
可將上述方程表示的方程改寫成以下形式

式中：控制量um=[(Δδe)t,(Δδp)t]，狀態量ym=[ΔVm,Δαm,Δqm,Δθm]；θ為控制量的常值誤差與比例誤差；εzu和εzy分別為控制量和狀態量的隨機誤差，其均值均為0，其協方差分別為Q和R。在此基礎上，采用四階龍格庫塔法得到式（8）的離散化形式

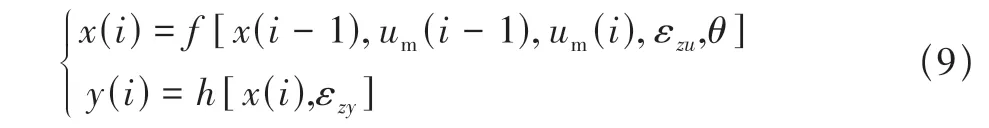
本文通過所構建的基于縱向小擾動線性模型的離散化系統方程進行仿真飛行試驗，以生成后續研究中所需的含異常數據的模擬飛行數據。首先將縱向小擾動線性模型參數以矩陣內元素的形式進行設定，并對輸入變量與輸出變量中的ΔV項進行無量綱化處理，設定模型參數值為

設置飛行數據采樣組數為500 組，飛行數據采樣頻率為20次/s。采用飛行試驗的典型動作“3211”信號[12]作為控制量數據，進行仿真飛行試驗，獲得后續研究中所需的含異常數據的模擬飛行數據。

1.2 野值的識別、剔除與補正

飛行數據中，野值的存在將降低試驗結果與基于它得到的辨識結果的可信度與精度。因此需要建立正確的準則，剔除真正的野值并加以補正[1]。本文通過低階多項式滑動擬合求得某點的期望值，測量值與期望值之差大于格魯布斯閾值時將該點識別為野值，采用七點二階多項前推差分算式[1]

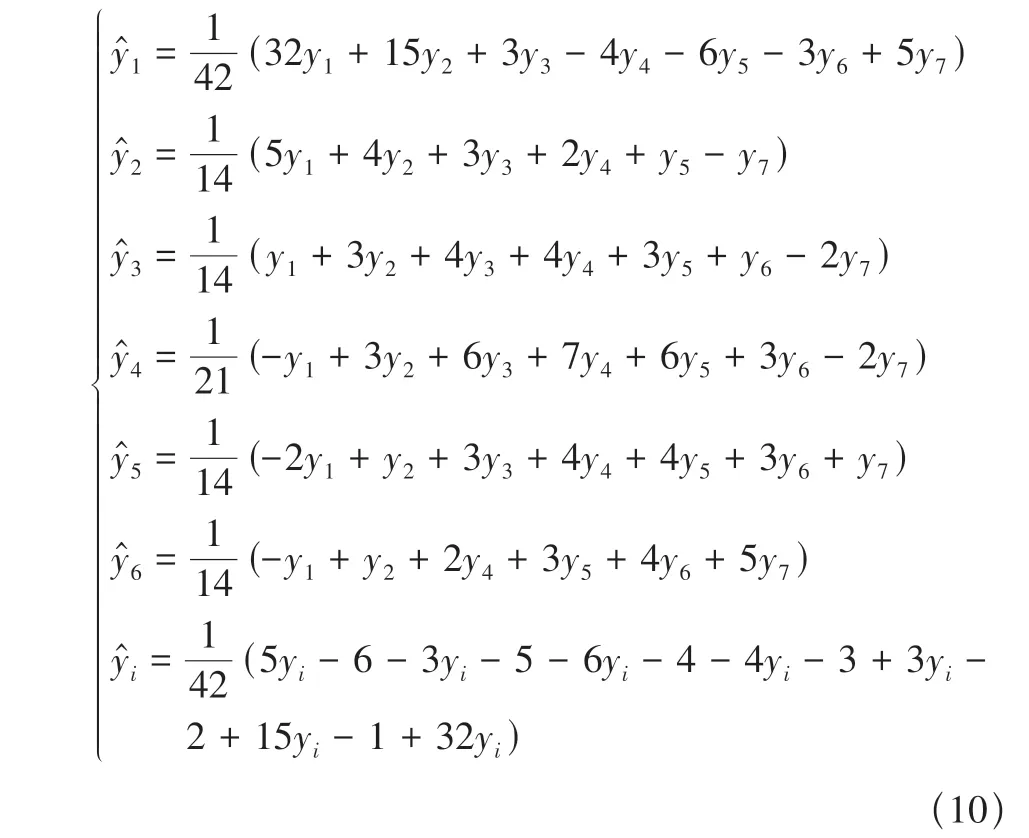
式中：i=7,8,9,…,N；yi與y?i分別為第i點的測量值與期望值。按數據順序逐點計算期望值y?i及新息vi=yi-y?i。取置信度α=99%，由格魯布斯臨界值表可知K(7,0.99)=2.097，滿足式（11）的點可視作野值點

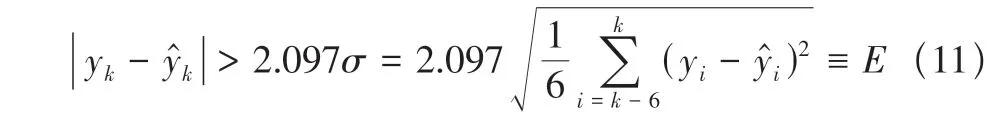
數據中可能出現較為接近的連續跳點，當k點為野值時，滿足式|yk+i-yk|＜E的點也為野值[1]。為避免將階躍信號誤識別為野值并將其剔除的情況發生，取m=3，當式（11）滿足k+i>k+3時，可以認為yk，yk+1，…，yk+m都為正常值[1]。在識別出已判定為野值的點并加以剔除后，采用以野值點前三點yk-3，yk-2，yk-1和后三點yk+m+1，yk+m+2，yk+m+3為已知值的六點拉格朗日插值進行野值點的補正[1]

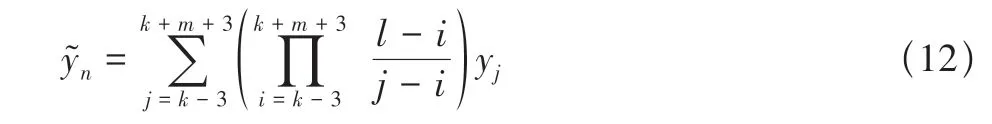
式中：滿足i，j≠k，k+1，…，k+m；i≠j；l=k，k+1，…，k+m。y?k,y?k+1,…,y?k+m為各野值點補正值。野值處理方法在模擬飛行數據上的應用實例如圖1所示，其中黑色、綠色圓圈分別代表識別出的野值點與野值補正點。

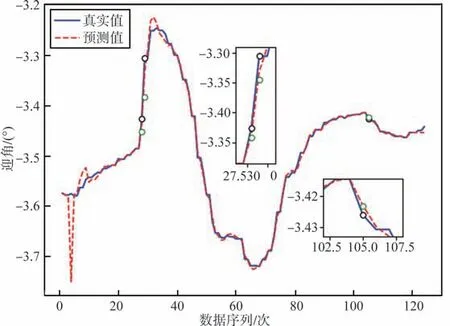
圖1 野值的識別、剔除與補正Fig.1 Identification,elimination and correction of outliers

由圖1 可以看出，野值補正點相較于識別出的野值點更貼合預測值曲線。該方法對飛行數據中的孤立野值點與連續跳點均具有較好的補正效果。

1.3 數據的平滑濾波

受機身振動、電磁干擾等因素影響，數據常含有測量噪聲，其使得計算殘差增大，從而導致氣動參數辨識過程難以收斂或辨識結果錯誤，因此必須濾除數據中的測量噪聲[8]。本文利用Savitzky-Golay法對數據進行平滑濾波。

Savitzky-Golay法的核心思想是對一定長度窗口內的數據點進行k階多項式擬合，用擬合值代替原始數值，從而實現高頻噪聲點的去除與原始數據序列的平滑[13]。對離散化數據而言，該方法實際上是一種移動窗口的加權平均算法，但是其加權系數是通過在滑動窗口內對給定高階多項式的最小二乘擬合得出[14]。將1.1節中生成的含異常數據的模擬飛行數據導入該方法，得到平滑濾波效果如圖2所示。

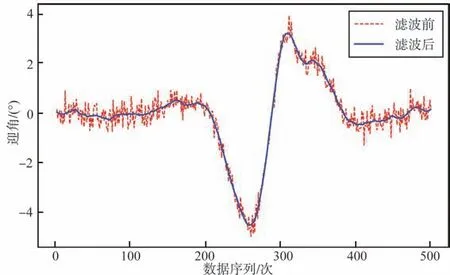
圖2 基于Savitzky-Golay法的數據的平滑濾波Fig.2 Smoothing filtering of data based on Savitzky-Golay method

由圖2 可以看出，Savitzky-Golay 法在飛行數據的平滑濾波中能夠在較好保持數據細節信息的同時濾除數據中的隨機誤差，能夠滿足飛行數據預處理的要求。

1.4 常值誤差與比例誤差的辨識與補償

本文數據中的零位誤差、時間延遲與比例誤差對狀態量的影響方式已在上文的離散化飛行數據相容性檢驗模型中得到確定，此時需要通過特定準則，將參數估計問題等價替換為求準則函數極值的問題，從而辨識出數據中的零位誤差、時間延遲與比例誤差。本文利用極大似然法進行數據中常值與比例誤差的辨識。對于給定的一組與待辨識參數θ有關的觀測量Z，極大似然法參數辨識的實質是通過不斷迭代，尋找使得選定的似然函數L取得極大值的參數θ?。當似然函數取為條件概率p(Z|θ)時，極大似然參數估計就是尋找使Z出現的條件概率達到極大值時對應的θ?[15]。通過基于觀測數據的統計學性質與假設的一系列化簡與轉化，得到似然準則函數為

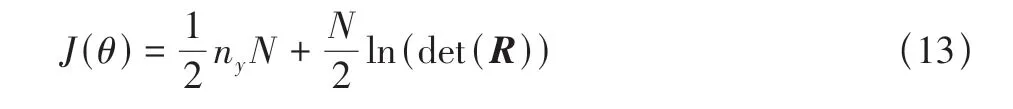
式中：ny為待辨識參數個數，N為觀測數據組數，R為量測誤差協方差矩陣，det(R)為矩陣R的行列式。此時，極大似然參數辨識可以轉化為在離散化飛行數據相容性檢驗模型的約束下，通過不斷迭代求得似然準則函數J(θ)取得極小值的θ?[16]。其基本流程如圖3所示。

圖3 極大似然法流程Fig.3 Flow chart of maximum likelihood method

1.4.1 零位誤差辨識與補償算例

選取待估計參數θ=[Δ(Δδe),Δ(Δδp)]，默認其他數據不含有零位誤差。向控制量數據加入大小為[-0.3(°),4]的零位誤差和方差均為10^(-2)的隨機誤差，并向狀態量數據加入方差均為10^(-1)的隨機誤差。采用matlab 中求多元非線性函數最小值函數“fmincon”迭代得到θ的最優解。零位誤差辨識值隨迭代次數變化過程與辨識結果如圖4與表1所示。

基于辨識值的控制量的零位誤差補償前后得到的狀態量響應曲線對比如圖5所示。

由圖4、圖5及表1可以看出，零位誤差辨識值隨迭代次數增加快速收斂至真值附近，且辨識結果具有較高精度。基于零位誤差補償后的控制量數據生成的狀態量數據與無零位誤差下的真實數據符合較好。

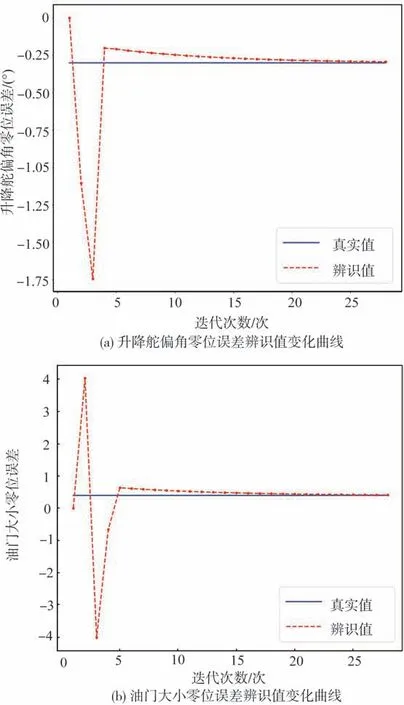
圖4 零位誤差辨識值隨迭代次數變化曲線Fig.4 Variation curve of the identification value of zero error with iteration times

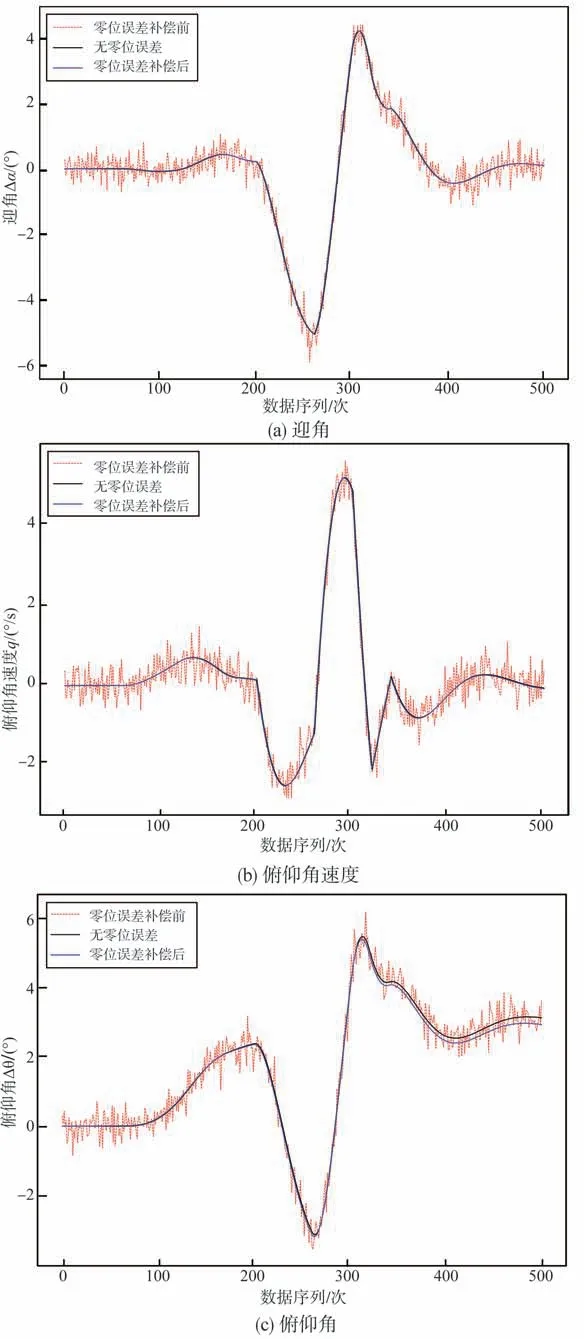
圖5 零位誤差補償前后響應曲線對比Fig.5 Comparison between response curves before and after zero error compensation

1.4.2 時間延遲辨識與補償算例

選取估計參數θ=[Δtδe，Δtδp]，默認其他數據不含有時間延遲。向控制量數據加入[8,-6]（單位：個采樣周期，本文取0.05s）的時間延遲，并向狀態量數據加入方差均為10^(-1)的隨機誤差。時延辨識值隨迭代次數變化過程與辨識結果如圖6和表2所示。

基于辨識值的控制量的時間延遲補償前后得到的狀態量響應曲線對比如圖7所示。

由圖6、圖7 及表2 可以看出，時間延遲辨識值的收斂較慢，中間還存在一些階梯狀變化，最終還是收斂于真值附近，且辨識結果具有較高精度。基于時間延遲補償后的控制量數據生成的狀態量數據與無時間延遲下的真實數據符合較好。

圖6 時間延遲辨識值隨迭代次數變化曲線Fig.6 Variation curve of the identification value of time delay with iteration times

圖7 時間延遲補償前后響應曲線對比Fig.7 Comparison between response curves before and after time delay compensation

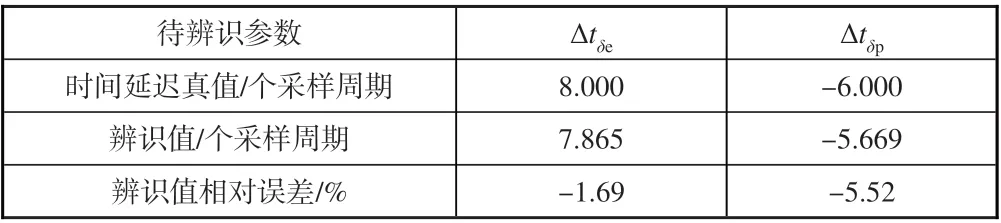
表2 時間延遲辨識結果Tabel 2 Identification result of time delay

1.4.3 比例誤差辨識與補償算例

選取待估計參數θ=[εyδe,εyδp]，默認其他數據不含比例誤差。向控制量數據加入大小為[0.6,-2.4]的比例誤差，并向狀態量數據加入方差均為10^(-1)的隨機誤差。

比例誤差辨識值隨迭代次數變化過程與辨識結果如圖8 和表3 所示。基于辨識值的控制量的比例誤差補償前后得到的狀態量響應曲線對比如圖9所示。

由圖8、圖9及表3可以看出，比例誤差辨識值隨迭代次數增加迅速收斂至真值附近，且辨識結果精度較高。基于比例誤差補償后的控制量數據生成的狀態量數據與無比例誤差下的真實數據符合較好。

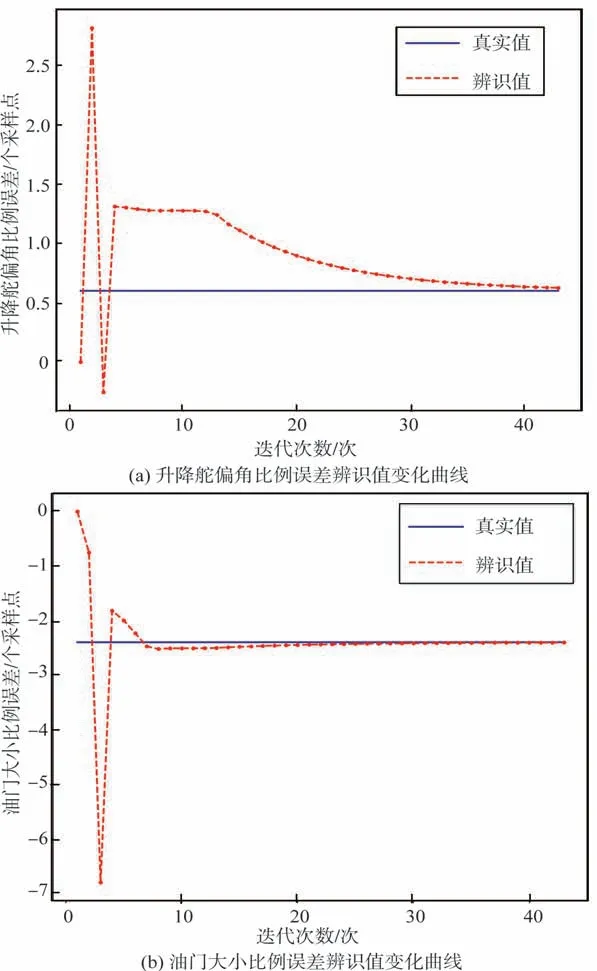
圖8 比例誤差辨識值隨迭代次數變化曲線Fig.8 Variation curve of the identification value of proportional error with iteration times

圖9 比例誤差補償前后響應曲線對比Fig.9 Comparison between response curves before and after proportional error compensation

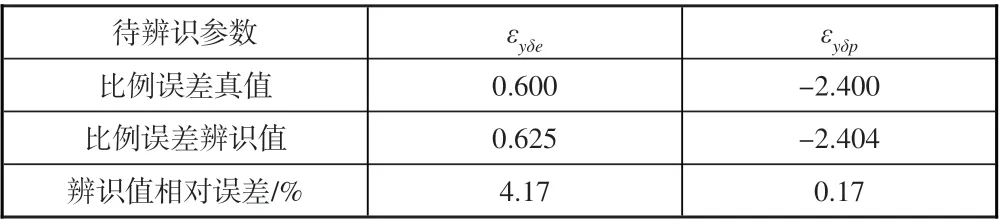
表3 比例誤差辨識結果Tabel 3 Identification result of proportional error

從上述算例中可以看出，本文提出的基于極大似然法的飛行數據處理方法可以較為快速精確地估計出各控制量數據相對于狀態量數據的零位誤差、時間延遲與比例誤差的大小，且基于補償后的控制量數據生成的狀態量數據更為貼合無控制量誤差下的真實狀態量數據。

2 飛行數據處理方法在模型參數辨識中的應用

在基于飛行數據進行飛行器模型參數辨識的實際應用中，通常已知的數據包括狀態量初值X0、通過理論計算或風洞試驗的氣動數據得到的氣動參數預估值θ0、飛行試驗中由傳感器收集到的控制量數據U0與狀態量觀測數據Z。其中的原始控制量數據U0常常含有大小未知的時間延遲與零位誤差，這可能給基于飛行數據的直接飛行器模型參數辨識造成不利影響，直接影響到飛行器的后續設計與優化工作。

基于此，本文圍繞控制量的常值誤差補償前后的飛行器模型參數辨識過程與結果間的對比，對所提出的飛行數據處理方法在飛行器模型參數辨識中的應用進行了研究。設定待辨識參數真值為

采用上文仿真飛行試驗中的仿真設置與模型、補償前后的控制量與狀態量數據，以上節內容中設定的縱向小擾動模型參數值作為待辨識參數初始值，基于極大似然法對模型參數進行辨識。

2.1 常值誤差補償前后控制量下的模型參數辨識結果

控制量的常值誤差補償前后，各待辨識模型參數（設定A、B矩陣中的參數A11、A12、A14、A21、A22、A31、A32、A33、B11、B21、B31，均為無量綱量）隨迭代次數的變化曲線如圖10 所示。其中黑色實線代表給定的待辨識參數真實值，紅、藍色虛線代表常值誤差補償前、后的模型參數辨識值變化曲線。

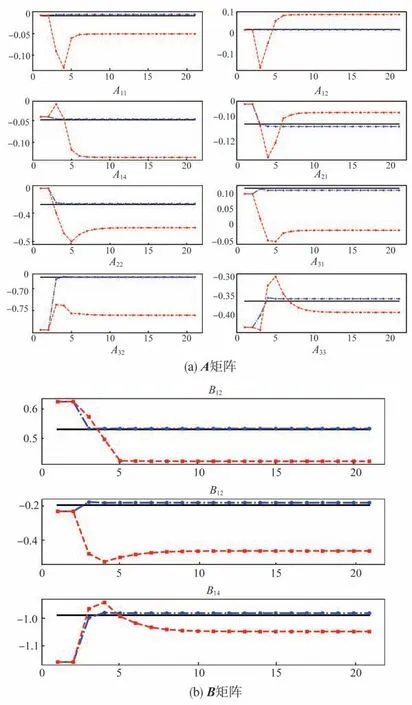
圖10 模型參數辨識值隨迭代次數變化曲線Fig.10 Variation curve of model parameter identification value with iteration times

由圖10 及表4 可以看出，控制量的常值誤差補償后的參數辨識過程收斂較快，且辨識精度更高。長、短周期模態是飛行器縱向運動的固有特性，是分析飛行器的縱向動穩定性的重要依據。本文分別對基于給定真實的系統矩陣A參數與通過常值誤差補償前后模型參數辨識值得到的系統矩陣A的縱向模態特征值進行計算與對比。由表5可以看出，常值誤差補償后模型參數辨識值下的系統矩陣A的縱向模態特征值在不同模態上更為接近給定真實的縱向模態特征值。由圖11可以看出，基于常值誤差補償后模型參數辨識值得到的狀態量數據更為貼近基于給定真實模型參數辨識值得到的狀態量數據。

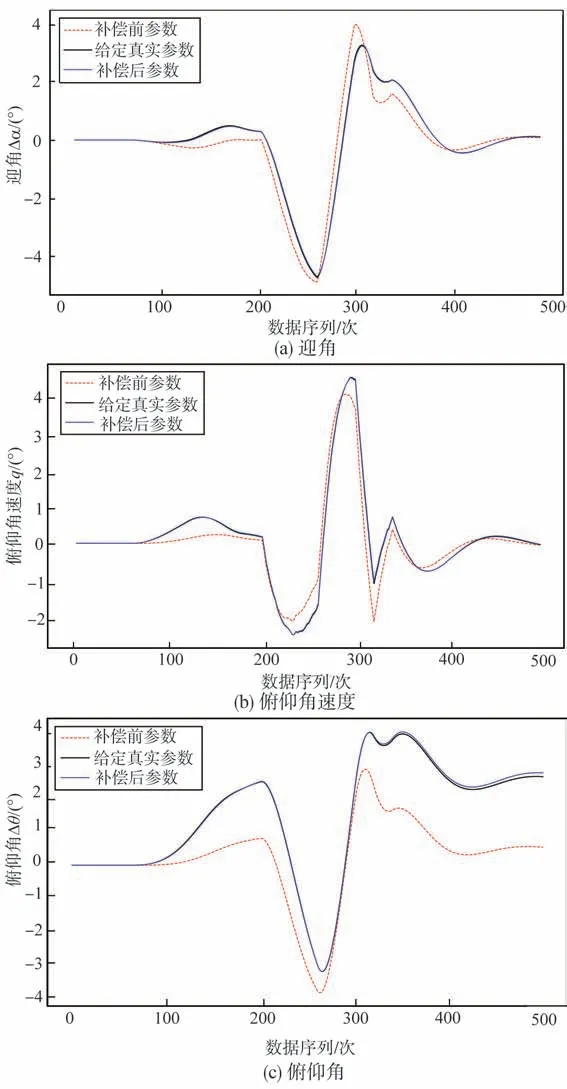
圖11 常值誤差補償前后模型參數得到的響應曲線對比Fig.11 Comparison between response curves obtained from model parameters before and after constant error compensation

表4 常值誤差補償前后模型參數辨識結果Tabel 4 Model parameter identification result before and after constant error compensation

表5 補償前后模型參數辨識結果的縱向模態對比Tabel 5 Longitudinal mode comparison of model parameter identification results before and compensation

2.2 結合常值誤差補償的模型參數辨識組合方法

在所設計的飛行數據處理方法及其在模型參數辨識中的應用的基礎上，本文進一步提出了結合常值誤差補償的飛行器模型參數辨識組合方法。其基本思路是：通過基于模型參數初始值與狀態量觀測數據的控制量常值誤差的辨識與補償環節和控制量常值誤差補償后的模型參數辨識環節的不斷迭代以及模型參數初始值的不斷更新，逐漸縮小狀態量計算數據Y與狀態量真實觀測數據Z之間的差異，從而使模型參數辨識值與控制量數據逐漸接近真實值。其流程如圖12所示。

圖12 結合常值誤差補償的參數辨識組合方法步驟Fig.12 Step diagram of the combination method of parameter identification combined with constant error compensation

3 結論

本文主要對飛行數據中異常數據的辨識與補償方法及其在飛行器模型參數辨識中的應用進行了研究，提出了一套從數據中野值與隨機誤差的消除，到結合數據相容性檢驗的時間延遲、零位誤差與比例誤差的辨識與補償的飛行數據處理方法，并結合模擬飛行數據中異常數據的辨識與補償實例驗證了本文所提方法的可行性。常值誤差補償前后的控制量數據下的模型參數辨識過程與結果之間的比較表明，本文提出方法中控制量數據的常值誤差辨識與補償能夠顯著改善飛行器模型參數辨識的迭代過程與結果的精度。基于上述內容，本文對結合常值誤差補償的飛行器模型參數辨識組合方法中的應用進行了設想。本文研究的內容對于進一步推動飛行器模型參數辨識在飛行器設計中的實際應用具有積極意義。后續研究將選用更多飛行器動力學模型與飛行數據種類構建數據相容性檢驗模型，以進一步拓寬本文所提方法的適用范圍。