任意殼線性彎曲與自由振動(dòng)分析的最小二乘無網(wǎng)格法

陳 衛(wèi)，楊健生，韋冬炎，諶亞菁，彭林欣,2,3

(1.廣西大學(xué) 土木建筑工程學(xué)院，南寧 530004;2.廣西大學(xué) 廣西防災(zāi)減災(zāi)與工程安全重點(diǎn)實(shí)驗(yàn)室，南寧 530004;3.廣西大學(xué) 工程防災(zāi)與結(jié)構(gòu)安全教育部重點(diǎn)實(shí)驗(yàn)室，南寧 530004)

殼作為一種重要的結(jié)構(gòu)元件被廣泛應(yīng)用于土木、航天、機(jī)械以及船舶等實(shí)際工程中。殼體理論經(jīng)過多年推動(dòng)發(fā)展，已日趨完善。對(duì)于特定的殼結(jié)構(gòu)形式解析解也相繼涌現(xiàn)。例如圓柱殼彎曲[1-3]、自由振動(dòng)精確解[4-6]，雙曲扁殼彎曲[7]及自由振動(dòng)[8]的精確解等。然而，由于殼結(jié)構(gòu)形狀的多變性，求解殼結(jié)構(gòu)問題的解析解復(fù)雜程度很高，手工計(jì)算極難完成，因此其相關(guān)問題的數(shù)值求解顯得尤為重要。這些數(shù)值方法包括有限單元法[9](finite element method,FEM)，邊界元法[10-11](boundary element method,BEM)，等幾何分析[12-13](isogeometric analysis,IGA)，小波伽遼金法[14](wavelet Galerkin method,WGM)等。

無網(wǎng)格法作為一種新興的數(shù)值方法，不依賴于網(wǎng)格和單元。基于移動(dòng)小二乘法構(gòu)造的高階連續(xù)形函數(shù)，能夠很好地逼近各類形狀殼，而且對(duì)薄板殼結(jié)構(gòu)存在的剪切及薄膜鎖死現(xiàn)象，只需提高形函數(shù)的階數(shù)，就可以完全避免。另外無網(wǎng)格較易實(shí)現(xiàn)自適應(yīng)分析，且在解決超大變形、裂紋擴(kuò)展及高速?zèng)_擊等問題上具有一定的優(yōu)勢(shì)。在國(guó)外，1996年，Krysl等[15]率先將移動(dòng)最小二乘法近似的無網(wǎng)格法應(yīng)用到薄殼結(jié)構(gòu)中，采用拉格朗日處理本質(zhì)邊界條件，分析了薄殼的彎曲問題。Noguchi等[16]在Krysl等的基礎(chǔ)上結(jié)合一階剪切變形理論，采用罰函數(shù)法處理本質(zhì)邊界條件，運(yùn)用無網(wǎng)格伽遼金法分析了厚殼彎曲問題。Li等[17]采用再生核粒子(reproducing kernel particle method，RKPM)近似的無網(wǎng)格法研究薄殼大變形問題。Liu等[18-19]根據(jù)Simo等[20]提出的幾何精確殼理論及基爾霍夫假設(shè)，采用基于移動(dòng)最小二乘近似的無網(wǎng)格法分別研究了薄殼的彎曲及振動(dòng)問題。Kim等[21]采用再生核粒子近似的無網(wǎng)格法分析了殼結(jié)構(gòu)設(shè)計(jì)靈敏度問題。Chen等[22]采用基于再生核粒子近似的無網(wǎng)格法，運(yùn)用穩(wěn)定節(jié)點(diǎn)積分，分析了殼結(jié)構(gòu)彎曲問題。Sayakoummane等[23]采用徑向基函數(shù)(radial basis function，RBF)近似的無網(wǎng)格法分析了殼結(jié)構(gòu)的彎曲問題。Jarak等[24-25]利用無網(wǎng)格局部彼得洛夫-伽遼金法(meshless local Petrov-Galerkin，MLPG)研究了殼的線性彎曲問題。Costa等[26]采用基于再生核粒子近似的無網(wǎng)格法分析殼的彎曲問題，并討論了拉格朗日、罰函數(shù)及Nitsche’s法三種處理本質(zhì)邊界方式的影響。在國(guó)內(nèi)，李迪等[27-28]采用Petrov-Galerkin無網(wǎng)格法研究了殼結(jié)構(gòu)的彈塑性大變形彎曲，利用了罰函數(shù)處理本質(zhì)邊界條件。葉翔[29]、王硯[30]與陳靠偉[31]采用基于圓柱殼基本理論與移動(dòng)最小二乘近似的無網(wǎng)格法研究了圓柱殼振動(dòng)特性，同樣采用罰函數(shù)法處理本質(zhì)邊界條件。然而，罰函數(shù)[32]在施加本質(zhì)邊界時(shí)，存在罰系數(shù)不易確定及系統(tǒng)矩陣對(duì)角元素變化等缺點(diǎn)，需要不斷嘗試才能得到精確值。本文將引入完全轉(zhuǎn)化法處理剛度、質(zhì)量矩陣，便可直接施加本質(zhì)邊界條件，容易實(shí)現(xiàn)且精度高。

綜上可知，采用無網(wǎng)格法分析任意殼的彎曲問題在國(guó)內(nèi)并不多見，且分析任意殼的自由振動(dòng)問題在國(guó)內(nèi)外未見相關(guān)報(bào)道。本文利用無網(wǎng)格法的優(yōu)點(diǎn)，基于移動(dòng)最小二乘近似[33]和一階剪切變形理論[34]，分析任意殼的線性彎曲及自由振動(dòng)問題。文末選用幾個(gè)不同形狀殼的算例，計(jì)算其彎曲或自振頻率，并與有限元或理論解進(jìn)行對(duì)比分析，以此來驗(yàn)證該方法在計(jì)算任意殼的線性彎曲及自振頻率的有效性及合理性。

1 任意殼的無網(wǎng)格基本方程

1.1 移動(dòng)最小二乘法

函數(shù)U(x)在區(qū)域Ω(x)內(nèi)的近似函數(shù)為

(1)

式中：pi(x)為矢量基函數(shù)；bi(x)為相應(yīng)系數(shù)；m為基函數(shù)個(gè)數(shù)。基函數(shù)通常使用多項(xiàng)式，如二維二次基(m=6)，pT(x,y)=[1,x,y,x2,xy,y2]。

根據(jù)加權(quán)移動(dòng)最小二乘法確定式(1)中bi(x)，即要求各點(diǎn)處誤差加權(quán)平方和L2模取最小值

(2)

式中：ω(x-xI)為權(quán)函數(shù)；n為區(qū)域Ωx中權(quán)函數(shù)大于零的節(jié)點(diǎn)數(shù)；UI為節(jié)點(diǎn)參數(shù)。本文權(quán)函數(shù)取

(3)

令L取最小值，并求偏導(dǎo)，最終可得U(x)的近似函數(shù)為

NI(x)=pT(x)A-1(x)BI(x)

(4)

NI(x)=pT(x)A-1(x)ω(x-xI)p(xI)

(5)

1.2 幾何模型

如圖1所示X=(x,y,z)是在笛卡爾坐標(biāo)系中的位置矢量，r=(r1,r2,r3)是轉(zhuǎn)換坐標(biāo)系中的位置矢量。ei是笛卡爾坐標(biāo)系中正交單位矢量，Vi是殼中面某一點(diǎn)的正交單位矢量。根據(jù)Mindlin板殼理論，殼上任意一點(diǎn)的位置矢量可用表示為

圖1 板殼幾何模型及映射技術(shù)Fig.1 Geometric model of shell and mapping technique

(6)

式中：Xmid為殼中面的點(diǎn)在笛卡爾坐標(biāo)系中的位置矢量；h為殼厚度(等厚度)；ri為轉(zhuǎn)換坐標(biāo)(r1，r2為殼中面內(nèi)的參數(shù)，r3為厚度方向的參數(shù))；V3為垂直殼中面的單位法向矢量；V1，V2，V3有如下關(guān)系

(7)

同樣，殼上任意一點(diǎn)的位移矢量參數(shù)可表示為

(8)

式中：umid為殼中面的點(diǎn)在笛卡爾坐標(biāo)系中的位移(u，v，w)，θ1，θ2分別為繞殼中面正交矢量V1，V2的轉(zhuǎn)角。

1.3 位移場(chǎng)近似

根據(jù)式(5)利用移動(dòng)最小二乘法逼近，則殼上任意一點(diǎn)的位置矢量及位移矢量參數(shù)可分別表示為

(9)

(10)

式(10)改寫成矩陣形式為

(11)

式中：[uI，vI，wI，θ1I，θ2I]T=UI為殼中面上第I個(gè)節(jié)點(diǎn)的節(jié)點(diǎn)參數(shù)；uI，vI，wI為殼中面上I節(jié)點(diǎn)沿著笛卡爾坐標(biāo)系x，y，z三個(gè)方向的位移；θ1I，θ2I為殼中面I節(jié)點(diǎn)繞I節(jié)點(diǎn)正交矢量V1，V2的轉(zhuǎn)角；n為殼中面節(jié)點(diǎn)個(gè)數(shù)。

式(9)的位置矢量對(duì)轉(zhuǎn)換坐標(biāo)系ri的偏導(dǎo)，可得到協(xié)變基矢量Gi(i=1,2,3)為

(12)

把式(9)代入式(12)，則有

(13)

其中，基矢量ei(i=1,2,3)在笛卡爾坐標(biāo)系中是正交的，即eiej=δij，而協(xié)變基矢量

Gi·Gj≠δij

(14)

根據(jù)對(duì)偶關(guān)系，則逆變基矢量Gj符合克羅內(nèi)克性質(zhì)

(15)

根據(jù)式(15)，則可推出逆變基矢量為

(16)

1.4 位移-應(yīng)變關(guān)系

根據(jù)協(xié)變基矢量及逆變基矢量關(guān)系，有應(yīng)變-關(guān)系如下

(17)

應(yīng)變分量εij可寫成矢量形式為

(18)

式中，?u/?ri為位移矢量u對(duì)轉(zhuǎn)換坐標(biāo)系ri的偏導(dǎo)，寫成矩陣形式為

(19)

(20)

式中，Aij(k)為Ai1或Ai2與單位基矢量ek的點(diǎn)積，Aij可寫為

(21)

其中，

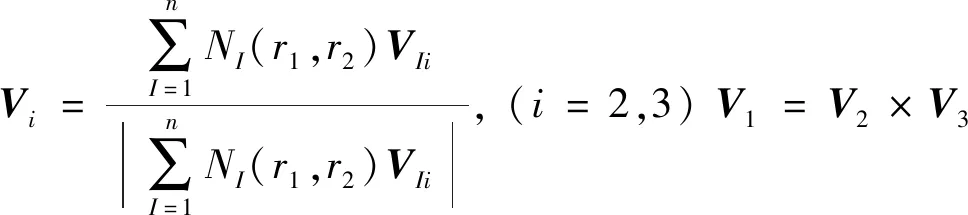
把式(19)、式(20)與代入式(18)可得應(yīng)變張量εij如下

(22)

應(yīng)變張量BI改寫為矩陣形式有

(23)

式中，Gi(j)為Gi與ej的點(diǎn)積。

1.5 本構(gòu)關(guān)系

對(duì)于線彈性材料，本構(gòu)關(guān)系有

σ=Dε

(24)

式中：σ為柯西應(yīng)力；C為四階彈性張量；通過正交單位矢量得到如下關(guān)系

D=DijklVi?Vj?Vk?Vl

(25)

其中，

式中：Ks為剪切修正因子,Ks=6/5；E為彈性模量；ν為泊松比。

基于協(xié)變基矢量及逆變基矢量，彈性張量D也可表示為

D=DijklGi?Gj?Gk?Gl

(26)

其中，

Dijkl=Dmnop(Vm·Gi)(Vn·Gj)(Vo·Gk)(Vp·Gl)

1.6 控制方程

殼在橫向荷載作用下的能量泛函為

(27)

式中：ρ為殼的密度；g為重力加速度；q為橫向均布荷載(板)；p為集中荷載。

將位移場(chǎng)公式(11)代入式(27)，并結(jié)合應(yīng)變方程式(22)，可得

(28)

其中，

由于本文算例中只考慮重力、集中荷載及板的橫向均布荷載，只列出這三種荷載類型。對(duì)于殼的法向均布荷載只需把荷載乘以x,y,z三個(gè)方向的方向余弦便可得到。x0為集中荷載作用點(diǎn)。

由最小勢(shì)能原理，泛函的變分ΠB=0，則殼彎曲控制方程為

KU=F

(29)

自由振動(dòng)時(shí)，節(jié)點(diǎn)參數(shù)uI，vI，wI，θ1I，θ2I都是關(guān)于時(shí)間t的函數(shù)，能量泛函為

(30)

其中，

(31)

式中：“‥”為關(guān)于時(shí)間t的二階偏導(dǎo)；ρ為密度。結(jié)合應(yīng)變方程式(22)，可得

(32)

其中，

(33)

根據(jù)Hamliton原理，由泛函的變分ΠV=0，則殼自由振動(dòng)控制方程為

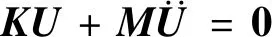
(34)

2 本質(zhì)邊界條件處理

基于MLS的無網(wǎng)格法不滿足克羅內(nèi)克條件，式(29)與式(34)的未知量是節(jié)點(diǎn)參數(shù)而非真實(shí)位移，不能像有限元法那樣直接施加本質(zhì)邊界條件。本文采用Chen等[35]提出的完全轉(zhuǎn)換法處理后，可以直接施加本質(zhì)邊界條件。

(35)

其中，

式中，UI為節(jié)點(diǎn)參數(shù)。式(35)兩邊同時(shí)乘以Λ-1得到

(36)

令T=Λ-1，變換式(36)有

(37)

把式(36)代入式(29)得到

(38)

式(38)兩邊同時(shí)乘以TT得到

(39)

式(39)可改寫為

(40)

同樣，式(34)可修改為

(41)

通過解如下方程特征值問題，可得到任意殼的自振頻率。

(42)

3 算 例

所有算例中影響域均采用方形，定義hr1=dmax×cr1,hr2=dmax×cr2。hr1為影響域r1方向長(zhǎng)度，hr2為影響域r2方向長(zhǎng)度，cr1為r1方向兩個(gè)相鄰節(jié)點(diǎn)的距離，cr2為r2方向兩個(gè)相鄰節(jié)點(diǎn)的距離，取dmax=3。采用高斯積分為3×3×2，基函數(shù)取m=6。所有模型采用ABAQUS建模時(shí)，均采用4節(jié)點(diǎn)殼單元(S4R)，結(jié)點(diǎn)數(shù)均大于1 000。所有算例中，記CCCC為四邊固支，SCSC為一鄰邊固支，另一鄰邊鉸接，SSSS為四邊鉸接。為了討論本文方法的收斂性，每個(gè)算例中均采用不同均勻布置的離散節(jié)點(diǎn)方案進(jìn)行分析，并將計(jì)算結(jié)果與精確解或者有限元解進(jìn)行對(duì)比分析。

3.1 平 板

平板是殼結(jié)構(gòu)形式的一種特殊形式。如圖2所示，方板尺寸為L(zhǎng)=20 m，厚度h=1 m，均布載荷P=1 N/m2，材料參數(shù)E=10 000 N/m2，泊松比ν=0.499 99(近似為不可壓縮材料)。由于對(duì)稱性取1/4結(jié)構(gòu)進(jìn)行分析。討論節(jié)點(diǎn)數(shù)布置方案對(duì)四邊固支及四邊簡(jiǎn)支板撓度的影響，計(jì)算結(jié)果和精確解[36]的對(duì)比曲線如圖3所示。從圖3可知，對(duì)簡(jiǎn)單的板結(jié)構(gòu)，利用較少的節(jié)點(diǎn)(5×5)也能得到很準(zhǔn)確的結(jié)果，取二次基函數(shù)m=6時(shí)，不存在體積鎖現(xiàn)象。

圖2 平板無網(wǎng)格模型Fig.2 Meshfree model of plate

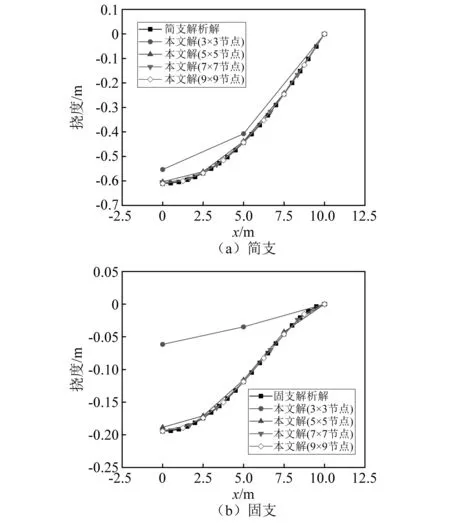
圖3 平板沿中心線的垂直位移Fig.3 Vertical displacement of plate along the center line

3.2 圓柱殼

如圖4所示，長(zhǎng)圓柱殼半徑R=5 m，長(zhǎng)度L=10.35 m，厚度h=0.094 m，材料的彈性模量E=10.5 MPa，泊松比ν=0.312 5，在圓柱殼中心點(diǎn)受一集中力P=100 N作用。集中力作用點(diǎn)豎向位移的解析解[37]為0.113 9 m，由于對(duì)稱性取1/8結(jié)構(gòu)進(jìn)行分析，收斂曲線如圖5所示。計(jì)算結(jié)果表明：隨著節(jié)點(diǎn)數(shù)增多，本文方法能有效地逼近有限元解，體現(xiàn)了本文方法良好的收斂性。

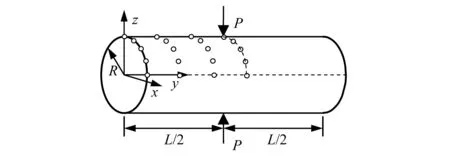
圖4 圓柱殼無網(wǎng)格模型Fig.4 Meshfree model of cylindrical shell

圖5 圓柱殼沿中心線的垂直位移Fig.5 Vertical displacement of cylindrical shell along the center line

3.3 屋頂殼

3.3.1 屋頂殼彎曲分析

如圖6所示，曲邊固支的屋頂殼半徑R=25 m，弧角度θ=40°，長(zhǎng)度L=50 m，厚度h=3 m，材料的彈性模量E=3 MPa，泊松比ν=0.3，密度ρ=9 kg/m3，重力加速度g=10 N/kg。由于對(duì)稱性取1/4結(jié)構(gòu)進(jìn)行分析，收斂曲線如圖7所示。研究表明，采用15×15節(jié)點(diǎn)離散時(shí)，本文方法計(jì)算結(jié)果與有限元解相比均在5%以內(nèi)，可認(rèn)為該離散方案使得該算例彎曲分析已收斂。

圖6 屋頂殼無網(wǎng)格分析模型Fig.6 Meshfree model of barrel vault roof

圖7 屋頂殼沿中心線的垂直位移Fig.7 Vertical displacement of barrel vault roof along the centerline

3.3.2 屋頂殼自振頻率分析

屋頂殼的幾何尺寸及其他無網(wǎng)格參數(shù)如同3.3.1節(jié)。取其全結(jié)構(gòu)計(jì)算邊界條件SSSS、SCSC和CCCC時(shí)屋頂殼的自振頻率，相關(guān)計(jì)算結(jié)果繪制于圖8及表1中。計(jì)算結(jié)果表明：對(duì)于屋頂殼的自振頻率分析，本文解的收斂速度快，只需9×9節(jié)點(diǎn)方案就可得到與有限元很相近的解(見圖8)；采用15×15節(jié)點(diǎn)方案時(shí)，本文解與有限元解的誤差均在1%以內(nèi)，有效驗(yàn)證本文方法的準(zhǔn)確性(見表1)。

圖8 屋頂殼SSSS邊界下自振頻率收斂性分析Fig.8 Convergence analysis of natural frequency of roof shell with SSSS boundary condition

表1 屋頂殼不同邊界下前10階自振頻率Tab.1 The first ten natural frequencies of barrel vault with different boundaries condition

3.4 雙曲扁殼

3.4.1 雙曲扁殼彎曲分析

如圖9所示，四邊固支(CCCC)的雙曲扁殼在中心點(diǎn)受P=4 N的集中力作用，扁殼的長(zhǎng)度L=6 m，厚度h=0.2 m，彈性模量E=30 000 N/m2，泊松比ν=0.3。集中荷載處撓度的解析解為0.010 6 m，由于對(duì)稱性取1/4結(jié)構(gòu)進(jìn)行分析，收斂曲線如圖10和圖11所示。研究表明：本文方法在分析雙曲扁殼時(shí)，除集中荷載處外，只需較少的節(jié)點(diǎn)就可以得到較好的計(jì)算結(jié)果(見圖10)；對(duì)雙曲扁殼彎曲分析，本文方法的收斂性比有限元快(見圖11)。

圖9 雙曲扁殼無網(wǎng)格模型Fig.9 Meshfree model of hyperbolic shallow shell

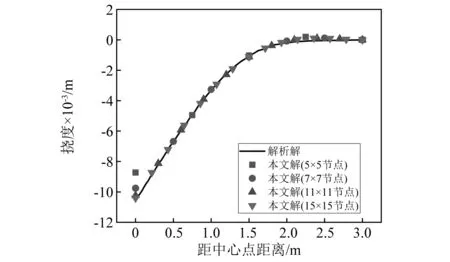
圖10 雙曲扁殼沿中心線的垂直位移Fig.10 Vertical displacement of hyperbolic shallow shell along the centerline

圖11 雙曲扁殼中心點(diǎn)垂直位移的收斂性Fig.11 Convergence of the vertical displacement of the center point of a hyperbolic shallow shell

3.4.2 雙曲扁殼自振頻率分析

雙曲扁殼的密度ρ=1 000 kg/m3，幾何尺寸及其他參數(shù)同3.4.1節(jié)，取其全結(jié)構(gòu)進(jìn)行分析。討論邊界條件為SSSS、SCSC和CCCC時(shí)雙曲扁殼自振頻率，相關(guān)計(jì)算結(jié)果繪制于圖12及表2。結(jié)果表明，本文方法在分析雙曲扁殼自由振動(dòng)時(shí)具有良好的收斂性及較高的精度。

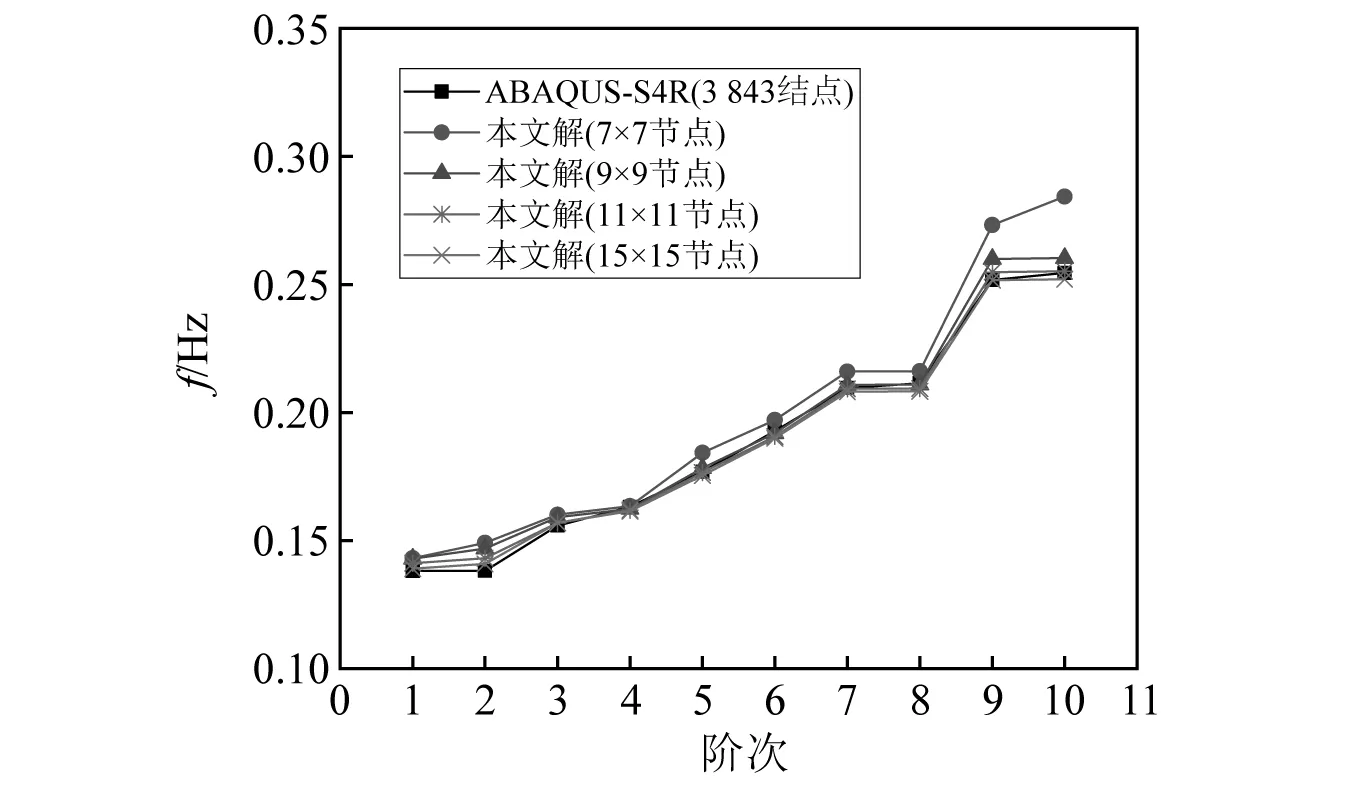
圖12 雙曲扁殼SSSS邊界下自振頻率收斂性分析Fig.12 Convergence analysis of natural frequency of hyperbolic shallow shell with SSSS boundary condition

表2 雙曲扁殼不同邊界下前10階自振頻率Tab.2 The first ten natural frequencies of hyperbolic shallow shell with different boundaries condition

3.5 波紋板自振頻率分析

如圖13和圖14所示，四邊固支(CCCC)的余弦波波紋板板長(zhǎng)L=1.8 m，W=1.8 m，板厚h=0.018 m，半波長(zhǎng)c=0.3 m，彈性模量E=30 GPa，泊松比ν=0.3，密度ρ=7 830 kg/m3，共3個(gè)完整波紋。幅值F=0.01時(shí)，波紋板在不同節(jié)點(diǎn)數(shù)離散方案情況下前10階的自振頻率如圖15所示。為驗(yàn)證本文方法求解波紋板自振頻率的適用性，討論波紋幅值F從0.01～0.04 m變化時(shí)，波紋板的自振頻率情況，相關(guān)計(jì)算結(jié)果列于表3。當(dāng)幅值F=0.04 m時(shí)，波紋板自由振動(dòng)的前3階模態(tài)如圖16所示。

圖16 波紋板(F=0.04 m)CCCC邊界下自由振動(dòng)前3階模態(tài)Fig.16 The first three modes of free vibration of corrugated plate (F=0.04 m) with four edges clamped (CCCC) boundary condition

表3 余弦波紋板四邊固支(CCCC)邊界下前10階自振頻率Tab.3 The first ten natural frequencies of corrugated plate with four edges clamped (CCCC) boundary condition

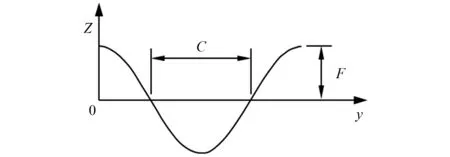
圖13 波紋板剖面示意圖Fig.13 Schematic diagram of corrugated plate section

圖14 波紋板無網(wǎng)格模型Fig.14 Meshfree model of corrugated plate

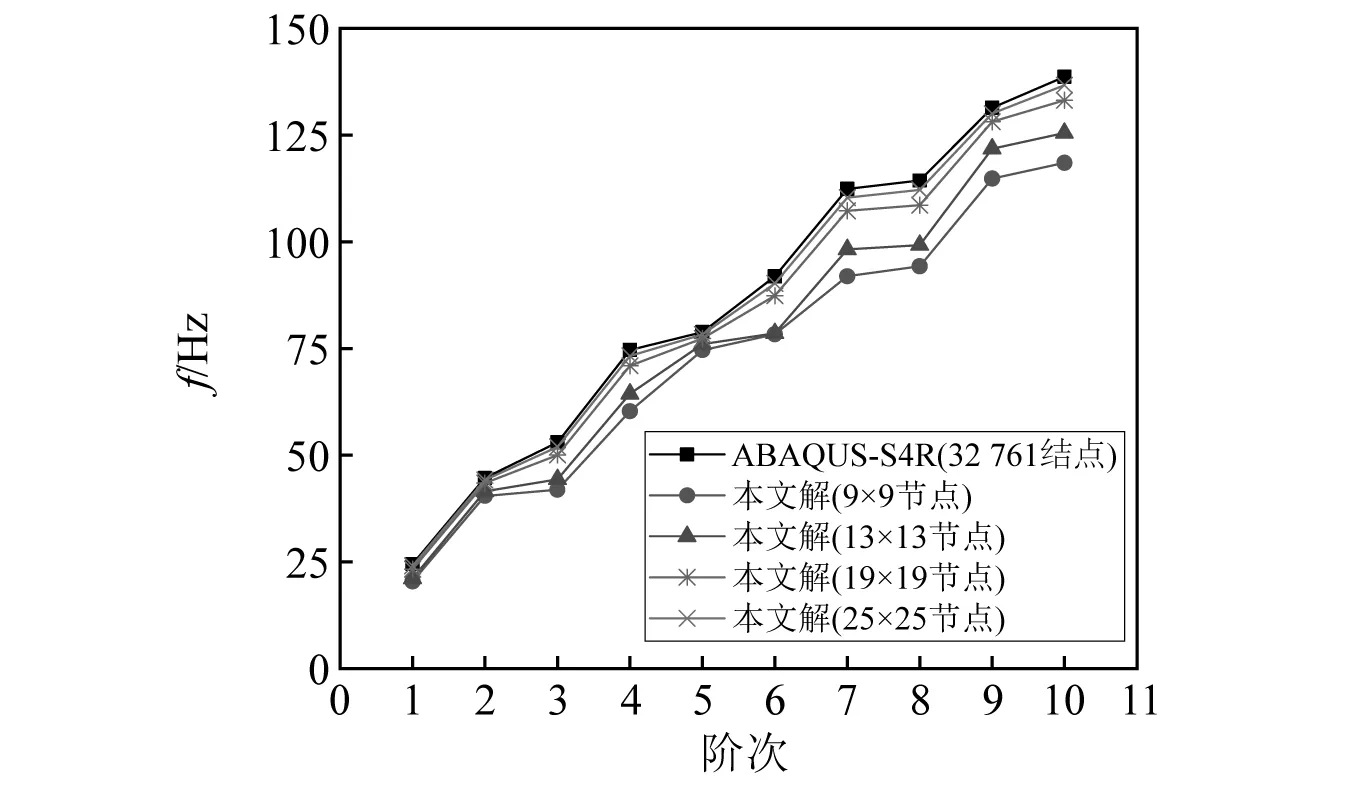
圖15 當(dāng)幅值F=0.01 m時(shí)波紋板自振頻率收斂性分析Fig.15 Convergence analysis of natural frequency of corrugated plate with amplitude F=0.01 m

研究表明：波紋板因其幾何形狀比屋頂殼及雙曲扁殼復(fù)雜，需布置更多的離散節(jié)點(diǎn)才能使計(jì)算結(jié)果收斂(對(duì)比圖15、圖12及圖8)；對(duì)于幅值F=0.01～0.04 m的波紋板，采用25×25節(jié)點(diǎn)離散方案得到的結(jié)果與有限元對(duì)比，誤差均在5%以內(nèi)。

4 結(jié) 論

本文基于移動(dòng)最小二乘法和一階剪切變形理論，推導(dǎo)了求解任意殼的無網(wǎng)格列式，采用完全轉(zhuǎn)換法處理邊界條件，計(jì)算了任意殼的線彈性彎曲及自振頻率問題，并與解析解及有限元解對(duì)比。結(jié)果表明：

(1) 本文方法計(jì)算任意殼的線性彎曲及自振頻率精度高，隨著節(jié)點(diǎn)的增加，計(jì)算結(jié)果數(shù)值穩(wěn)定地趨近解析解或有限元解，表現(xiàn)出良好的收斂性。

(2) 計(jì)算所得的彎曲撓度、自振頻率與解析解或有限元解很接近，其中自振頻率的結(jié)果與有限元解之間的誤差均在5%以內(nèi)，驗(yàn)證了該方法的有效性。

(3) 采用基于移動(dòng)最小二乘近似的無網(wǎng)格法求解任意殼，前處理簡(jiǎn)單，只需少量的節(jié)點(diǎn)信息，就能很好逼近不同形狀殼結(jié)構(gòu)形式，且可以有效地避免有限元中復(fù)雜的網(wǎng)格劃分及網(wǎng)格畸變的影響，在工程實(shí)踐中具有廣闊的應(yīng)用前景。