沉積條件對化學氣相沉積SiC涂層沉積速率的影響

徐振男，張立強，陳招科，霍皓靈，張浩然

(1. 中南林業科技大學機電工程學院，湖南 長沙，410004；2. 中南大學粉末冶金國家重點實驗室，湖南 長沙，410083)

2011-03-12，日本福島第一核電站發生嚴重的核事故，主要原因是海嘯導致海水倒灌破壞冷卻機泵致使冷卻水不能正常循環，鋯合金燃料包殼管在高溫下與水蒸氣發生鋯水反應，產生大量氫氣，并引發氫爆[1-3]。由此之后，可代替鋯合金作為燃料包殼管的新材料的開發和研究受到了研究者的重點關注。核級連續碳化硅纖維增強碳化硅基體(SiCf/SiC)復合材料由于在中子輻照下具有高的尺寸穩定性和低的誘導放射性，同時具有偽塑性斷裂模式，可設計的物理性能和力學性能，被認為是理想的水冷堆包殼管候選材料，并可應用于其他核反應堆的第一壁、偏濾器以及流道插件等部件[4-6]。

核級SiCf/SiC 復合材料由第三代SiC 纖維、少量的PyC 界面以及化學氣相滲透/沉積獲得的SiC基體和涂層組成核燃料包殼管要求直徑小，長度長，即大長徑比。這種結構對包殼管軸向基體和涂層的均勻性提出了更高的要求[7-9]。

化學氣相沉積法廣泛應用于制備SiC 涂層[10-13]。CVD SiC涂層過程中，氣態物質擴散和產物沉積反應之間的相互作用十分復雜，而且各項工藝參數對CVD SiC 涂層過程的影響也非常復雜[8,14]，若僅依靠實驗方法，則會耗費大量人力物力，有限元仿真技術為探究工藝參數影響CVD SiC涂層沉積速率提供了新的方法。LI等[15]建立了parallel-consecutive 模 型 和bimodal pore 模 型 來 模擬反應物在不同孔隙率中的擴散，發現在化學氣相滲透過程中會出現連續高密度區而影響致密化，通過改變工藝參數可以改變連續高密度區域出現的時間和地點。曾慶豐等[16-17]建立了耦合反應器的等溫化學氣相滲透過程的數學模型，分析了反應爐內的流場、溫度場、濃度場等，發現滲透均勻性與預制件結構密切相關。LI 等[18]對化學氣相沉積的抑制機理進行了仿真，仿真過程揭示了碳纖維體積分數為7.1%和14.2%的碳氈的致密化過程，數值模擬的密度分布與實驗結果吻合良好。成來飛等[19-20]采用有限單元法，實現了預制體內大、小孔的等溫化學氣相滲透過程的致密化行為的數值模擬，發現了降低溫度有利于滲透均勻性但會延長致密化時間。李沙等[21]模擬了2種構型的立式反應爐中反應氣體的流動過程，發現反應爐流場分布會對CVD產生較大影響，多孔型CVD爐內反應氣體滯留時間過長，直通型CVD 爐內流場會產生明顯渦流。目前對計算機仿真CVD 的研究已較為成熟[22-23]，但國內外對大長徑比(長度為1～4 m)的CVD SiC 涂層的有限元仿真較少。本文作者根據CVD SiC涂層的工藝特點和大長徑比的結構特點，對長度為2 250 mm的CVD爐建立有限元模型，仿真分析工藝參數對SiC涂層沉積速率的影響，為實驗研究提供理論依據。

1 有限元模型建立

1.1 幾何模型

應用solidworks軟件建立化學氣相沉積爐工作區幾何模型，模型結構如圖1所示。

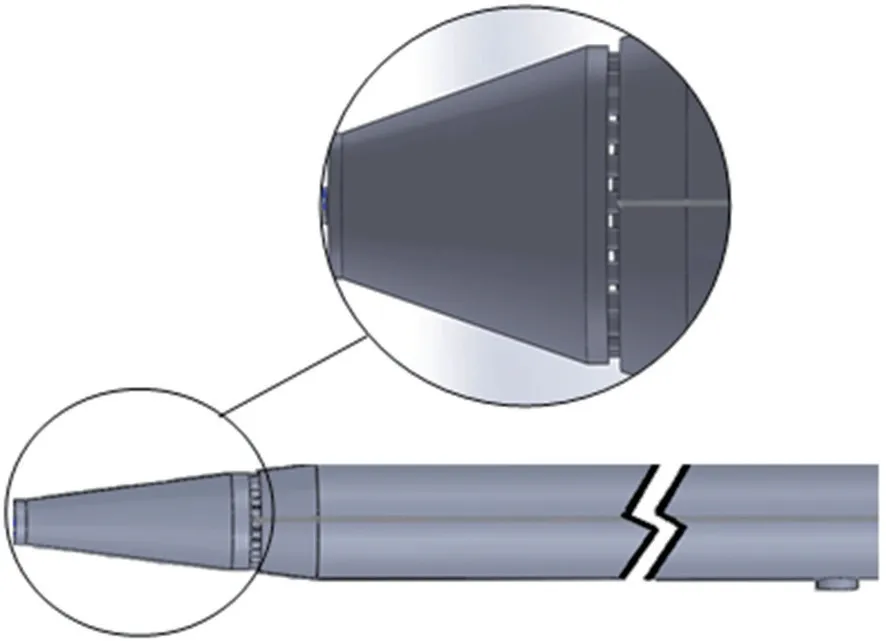
圖1 化學氣相沉積爐工作區幾何模型Fig.1 Geometric model of working area of chemical vapor deposition vessel

1.2 網格劃分

應用Fluent meshing 對化學氣相沉積爐工作區幾何模型進行網格劃分，采用基于“馬賽克”技術的Poly-Hexcore 方法生成體網格，在基體部分進行局部網格加密處理以便更加精確地對沉積速率進行分析。又因為反應爐工作區為對稱圓柱體，在保證計算精度的前提下減少計算量，構建的三維對稱CVD SiC有限元模型如圖2所示。

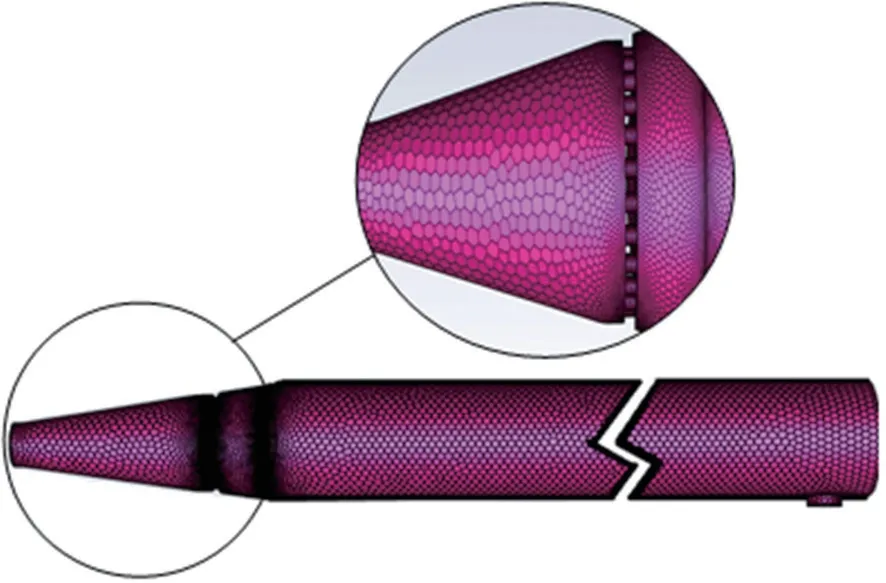
圖2 化學氣相沉積爐工作區網格劃分Fig.2 Grid division of working area of chemical vapor deposition vessel

1.3 模型假設

CVD SiC 涂層采用三氯甲基硅烷(CH3SiCl3，簡稱MTS)裂解生成SiC，其反應過程十分復雜，包括組分輸運及表面反應沉積，同時具有許多中間反應。仿真模擬的主要目的是研究工作區各種工藝參數對SiC涂層沉積速率的影響，因此，用總反應來描述MTS裂解的化學反應動力學過程：

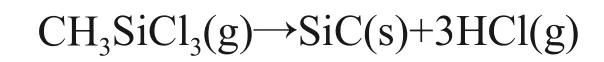
另外，在不影響結果的前提下進行如下假設：1)通過反應爐的氣體密度為常數；2)MTS 裂解反應過程中的反應氣體質量守恒；3)固壁，即流體與工作區所有壁面均采用無滑移壁面；4)不考慮輻射效應，忽略MTS裂解反應過程中產生的熱量，反應爐中的溫度保持恒定；5)假設氣體為理想氣體，符合理想氣體狀態方程。

式中：P為理想氣體的壓強，Pa；V為理想氣體的體積，m3；T為熱力學溫度，K；n為理想氣體的物質的量，mol；R為理想氣體常數，8.314 J/(mol·K)。

1.4 控制方程及邊界條件

根據傳熱傳質學的基本規律，化學氣相沉積爐內涉及復雜的化學反應及物質的傳遞，整個過程遵循基本的能量守恒、動量守恒及物質守恒方程[24]。求解過程為穩態過程，化學氣相沉積爐入口為速度入口，出口為壓力出口，無滑移壁面。

通過下式計算求得雷諾數，確定組分輸運過程為層流：

式中：Re為雷諾數；ρ為通入氣體密度，kg/m3；v為氣體流速，m/s；d為立式化學氣相沉積爐入口直徑，m；μ為通入氣體的動力學黏度，kg/(m·s)。

MTS 的反應速率常數隨溫度變化符合阿侖尼烏斯關系：

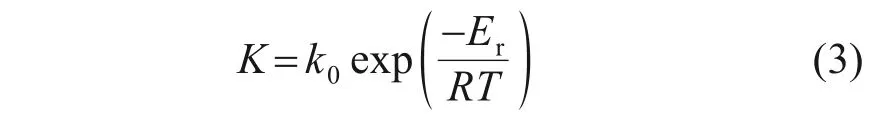
式中：k0為指前因子，m/s；Er為反應活化能，J/mol。

1.5 初始條件

為研究反應溫度、爐壓、載氣H2流量以及基體數量對CVD SiC 涂層沉積速率的影響規律，而這些因素對CVD SiC 涂層沉積速率的影響并非完全獨立，本文采用單因素試驗方案設計，通過將其他工藝參數保持在正常水平范圍值，來分析特定工藝參數對CVD SiC 涂層沉積速率的影響。仿真采用工藝參數變量與水平如表1所示。

表1 CVD SiC涂層仿真變量因子與水平Table 1 factors and levels of variable for CVD SiC coatings simulation

2 仿真結果分析與討論

2.1 反應溫度對SiC涂層沉積速率的影響

反應溫度是影響CVD SiC 涂層沉積速率的重要參數之一，在Ar 流量為1 200 mL/min、載氣H2流量為1 600 mL/min、爐壓為400 Pa、基體數量為4 根的條件下，仿真分析反應溫度對SiC 涂層的沉積速率的影響。圖3所示為不同溫度下SiC涂層沉積速率隨沉積位置的變化曲線。由圖3 可以看出：在900～1 150 ℃條件下，SiC 涂層沉積速率變化趨勢較為平穩，并且隨著溫度升高，沉積速率也隨之增大；在1 200～1 350 ℃條件下，SiC 涂層沉積速率變化較為劇烈。當沉積位置由-1 500 mm 至-1 100 mm 時，靠近進氣口區域SiC 涂層沉積速率下降較快；當沉積位置由-1 100 mm 至0 mm 時，遠離進氣口區域SiC 涂層沉積速率變化較為平緩，并且隨著溫度升高，SiC 涂層沉積速率反而降低。這是由于在900～1 150 ℃時，沉積速率受表面化學動力學，如化學吸附、化學反應、表面遷移、晶格重組和化學解吸等控制。在這種沉積機理控制下，反應物的消耗對膜層的沉積速率影響不大，所以，制備的膜層比較均勻。當溫度高于1 200 ℃時，表面化學反應進行得很快，沉積速率主要決定于氣相反應物通過邊界層向基體表面的擴散，這時反應受質量傳輸控制。由于化學解吸加快和反應副產物的腐蝕作用，沉積速率隨溫度升高而降低。

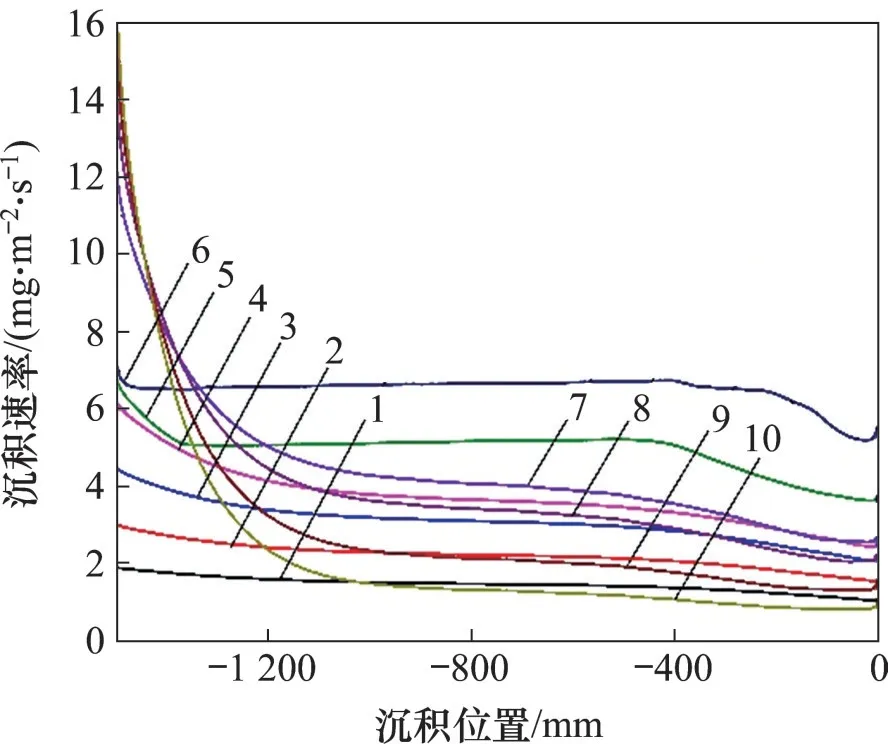
圖3 不同溫度下CVD SiC涂層沉積速率隨沉積位置的變化Fig.3 Deposition rates of CVD SiC coatings vary with deposition positions at different temperatures

2.2 爐壓對SiC涂層沉積速率的影響

爐壓會影響分子間的平均自由程從而影響氣體的擴散系數，改變爐壓將直接影響氣體在化學氣相沉積爐內輸運，進而影響SiC 涂層沉積速率。根據反應溫度對SiC涂層沉積速率的影響分析可以知道在900～1 200 ℃條件下SiC 涂層沉積均勻性較好，因此，選用溫度為1 000 ℃、Ar 流量為1 200 mL/min、載氣H2流量為1 600 mL/min、基體數量為4根的條件下，仿真分析爐壓對SiC涂層的沉積速率的影響。圖4所示為不同爐壓下SiC涂層沉積速率隨沉積位置的變化曲線。從圖4可知：在不同爐壓條件下，隨爐壓增大，SiC涂層沉積速率逐漸降低，并且沉積均勻性較差。這是因為較低的爐壓可以使MTS 的分子間的平均自由程增大，從而提高氣體的擴散系數，加快MTS 的輸運速率，減小MTS 分子間的不均勻性，提高SiC 涂層的沉積均勻性，這對大長徑比的CVD SiC 涂層沉積速率與沉積均勻性影響較大。

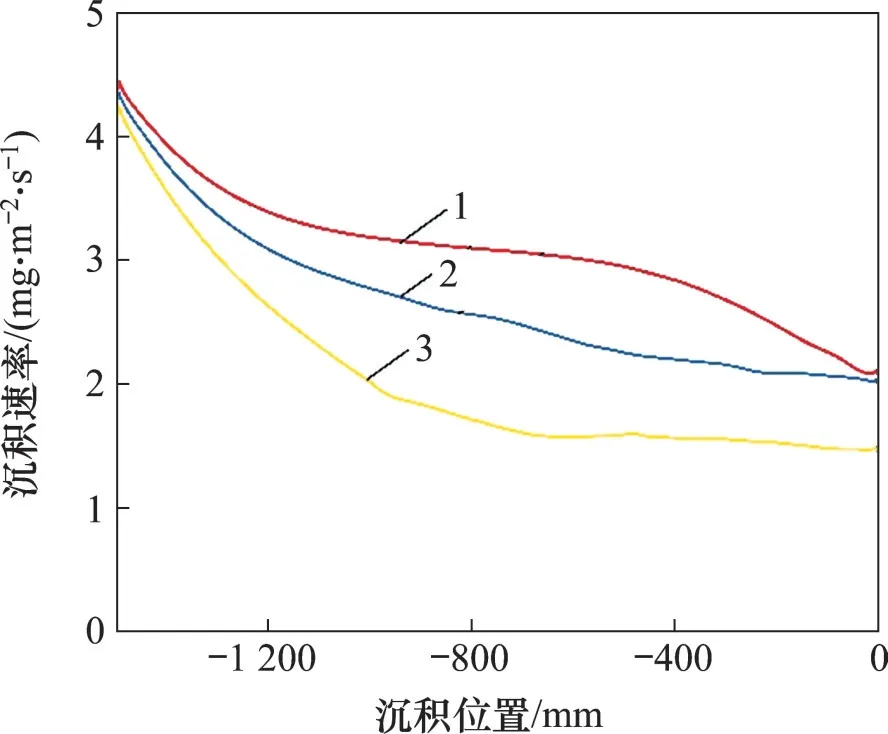
圖4 不同爐壓下CVD SiC涂層沉積速率隨沉積位置的變化Fig.4 Deposition rates of CVD SiC coatings vary with deposition positions at different vessel pressures

2.3 載氣H2流量對SiC涂層沉積速率的影響

在CVD SiC 涂層過程中，反應氣體MTS 是通過鼓泡法由載氣H2帶入反應腔內，因此，載氣H2的質量與MTS 的質量有嚴格的配比[25]，并將直接影響SiC涂層沉積速率。根據爐壓對SiC涂層沉積速率的影響分析可以知道，當爐壓為400 Pa 時，SiC涂層沉積速率較高。選用Ar流量為1 200 mL/min、爐壓為400 Pa、溫度為1 000 ℃、基體數量為4根，仿真分析載氣H2流量對SiC 涂層的沉積速率的影響，圖5所示為不同載氣H2流量下SiC涂層沉積速率隨沉積位置的變化曲線。由圖5可以看出：隨載氣H2流量增加，SiC 涂層沉積速率逐漸增大。同時，在載氣H2流量為1 000～1 200 mL/min 的條件下，SiC涂層沉積速率的變化幅度較小，沉積均勻性更好。這是因為進氣口截面直徑不變，隨著載氣H2流量增加，混合氣體流速增大，混合更為均勻。但隨著載氣H2流量增大到1 400～1 600 mL/min時，混合氣體流速也繼續增加，MTS 在基體表面停留時間較短，SiC涂層沉積均勻性較差。

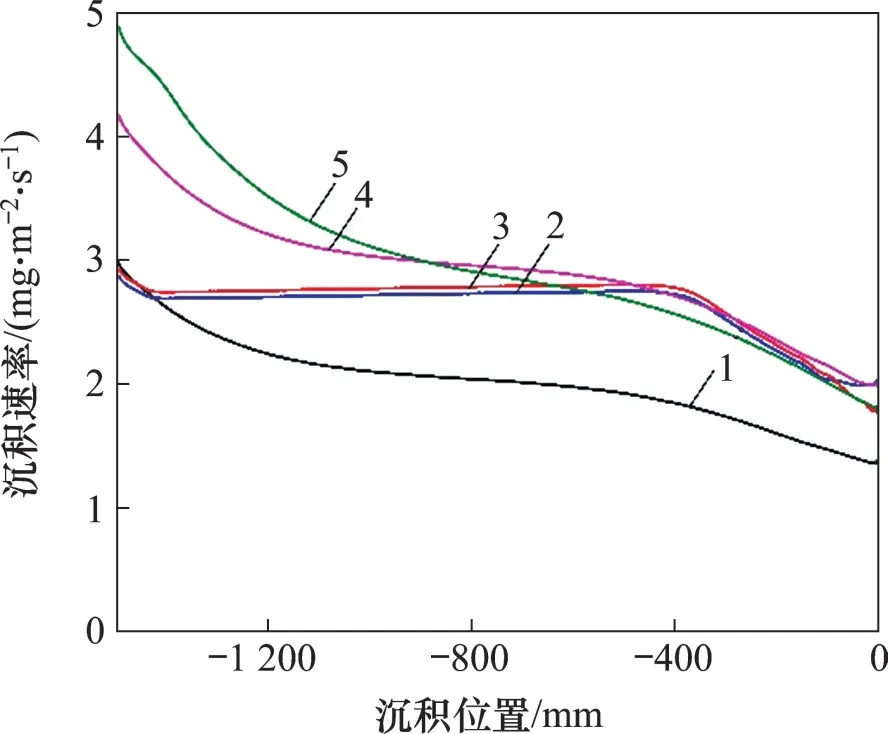
圖5 不同載氣H2流量下CVD SiC涂層沉積速率隨沉積位置的變化Fig.5 Deposition rates of CVD SiC coatings vary with deposition positions at different carrier gas H2 flow rates

2.4 基體數量對SiC涂層沉積速率的影響

不同基體數量也會影響化學反應沉積爐內的流場，進而影響SiC 涂層沉積速率。根據載氣H2流量對SiC涂層沉積速率的影響分析可以知道當載氣H2流量為1 000～1 200 mL/min時，SiC涂層沉積均勻性較好，選用Ar 流量為1 200 mL/min、載氣H2流量為1 000 mL/min、爐壓為400 Pa、溫度為1 000 ℃，仿真分析基體數量對SiC 涂層的沉積速率的影響，圖6所示為不同基體數量下SiC涂層沉積速率隨沉積位置的變化曲線。從圖6 可以看出：當基體數量在20 根以內時，隨著基體數量增加，SiC涂層沉積速率逐漸降低且沉積均勻性變差。這是因為當載氣H2流量與稀釋氣體Ar 流量恒定時，MTS在化學反應沉積爐內的質量分數也保持一定，當基體數量增多時，MTS氣體分散在各個基體上，進而影響SiC涂層沉積速率。

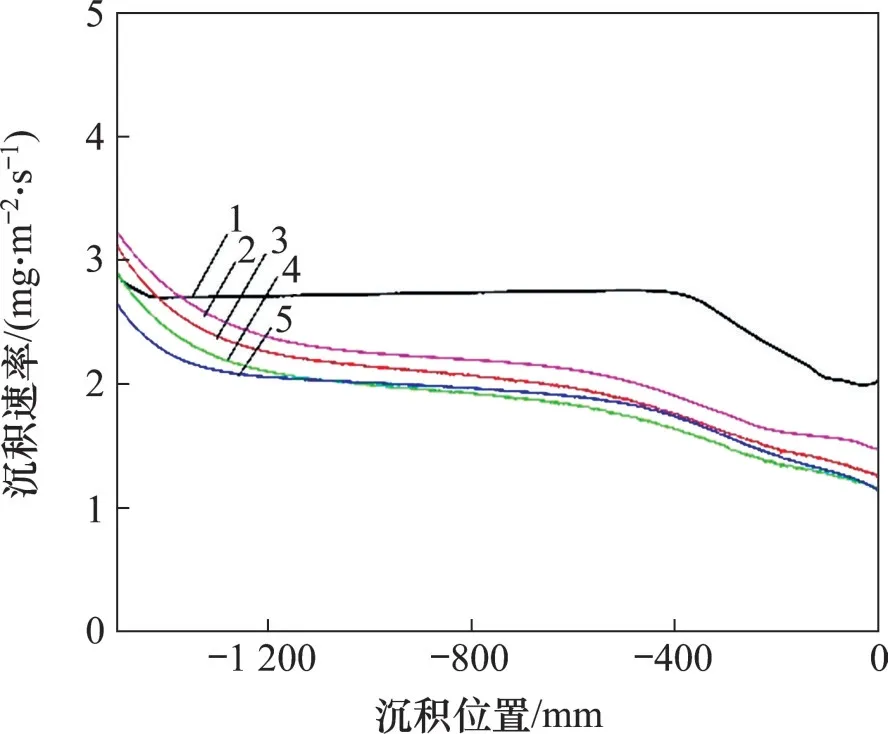
圖6 不同基體數量下CVD SiC涂層沉積速率隨沉積位置的變化Fig.6 Deposition rates of CVD SiC coatings vary with deposition positions at different number of substrates

3 CVD SiC涂層實驗

3.1 實驗條件與實驗過程

為驗證模型的準確性，在有限元仿真優化結果基礎上，進行相應的實驗。實驗條件如下：反應溫度為1 000 ℃左右，爐壓為400 Pa，Ar流量為1 200 mL/min，載氣H2流量為1 000 mL/min。采用化學氣相沉積法在直徑×長度為280 mm×2 250 mm立式化學氣相沉積爐內制備SiC涂層，1 500 mm長基體由化學氣相沉積爐上方吊入，假定上方吊入位置為原點，則反應氣體流動方向由-1 500 mm至0 mm。以H2為載氣，通過鼓泡法將源氣體MTS通入化學氣相沉積爐內，MTS裂解產生SiC沉積在基體表面。采用掃描電子顯微鏡(SEM)觀察產物的沉積厚度，通過X射線衍射(XRD)確定產物中存在的物相。

3.2 實驗結果分析與討論

3.2.1 CVD SiC涂層沉積速率變化

對1 500 mm 長CVD SiC 涂層樣品每隔50 mm取長×度為10 mm×10 mm 樣品，共取31 個，利用電子天平對沉積前后的樣品稱量，并根據下式計算得到樣品不同位置SiC涂層沉積速率r。

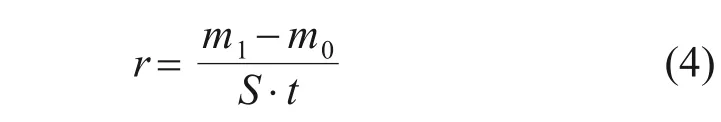
式中：m0為沉積前碳紙樣品的質量，kg；m1為沉積后基體的質量，kg；S為基體樣品的表面積，m2；t為沉積時間，s。

對SiC涂層沉積均勻性表征，采取下式計算其均勻性：

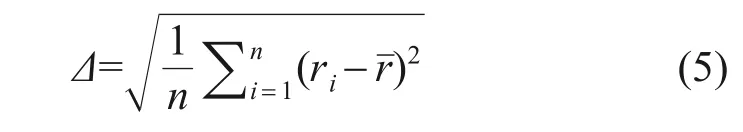
式中：Δ為涂層均勻性的標準差；ri為不同沉積位置的沉積速率；rˉ為平均沉積速率。Δ越小說明沉積越均勻，標準差Δ=2.172 38×10-7，表明SiC涂層沉積均勻性較好。

圖7所示為SiC涂層沉積速率隨沉積位置變化的模擬與實驗對比曲線。從圖7可知：當沉積位置由-1 500 mm 至-400 mm 時，靠近進氣口區域SiC涂層沉積速率變化較小；當沉積位置從-400 mm至0 mm 時，遠離進氣口區域SiC 涂層沉積速率下降較快，總體上是沿著反應氣體流向呈遞減的規律，仿真結果與實驗結果具有相同的變化趨勢，且平均相對誤差不大于8.3%，證實了本文所建立的有限元模型的可靠性。

圖7 在基體不同位置沉積速率仿真與實驗對比Fig.7 Comparison of deposition rates between simulation and experiment at different positions of carbon paper

3.2.2 CVD SiC涂層微觀結構

將CVD SiC 涂層每隔300 mm 取長×寬為10 mm×10 mm 樣品，共5 個，取樣位置分別編號為A，B，C，D和E。當Ar 流量為1 200 mL/min、載氣H2流量為1 000 mL/min、反應溫度為1 000 ℃、爐壓為400 Pa時，不同沉積位置SiC涂層的X射線衍射圖譜如圖8 所示。從圖8 可知：在2θ為35°，60°，72°以及75°左右出現的峰對應β-SiC 中的(111)，(220)，(311)和(222)晶面的衍射峰，說明在CVD 過 程 中 得 到 的SiC 為β 型。當Ar 流 量 為1 200 mL/min、載氣H2流量為1 000 mL/min、反應溫度為1 000 ℃、爐壓為400 Pa 時，1 500 mm 長CVD SiC 涂層不同沉積位置的SEM 圖像如圖9 所示。從圖9 可以看出：SiC 涂層沉積較為平整，當沉積位置遠離進氣口時，SiC 沉積厚度逐漸變小，表明沉積速率沿氣流方向逐漸降低，結果與仿真結果一致，進一步證實了本文所建立的有限元模型的可靠性。

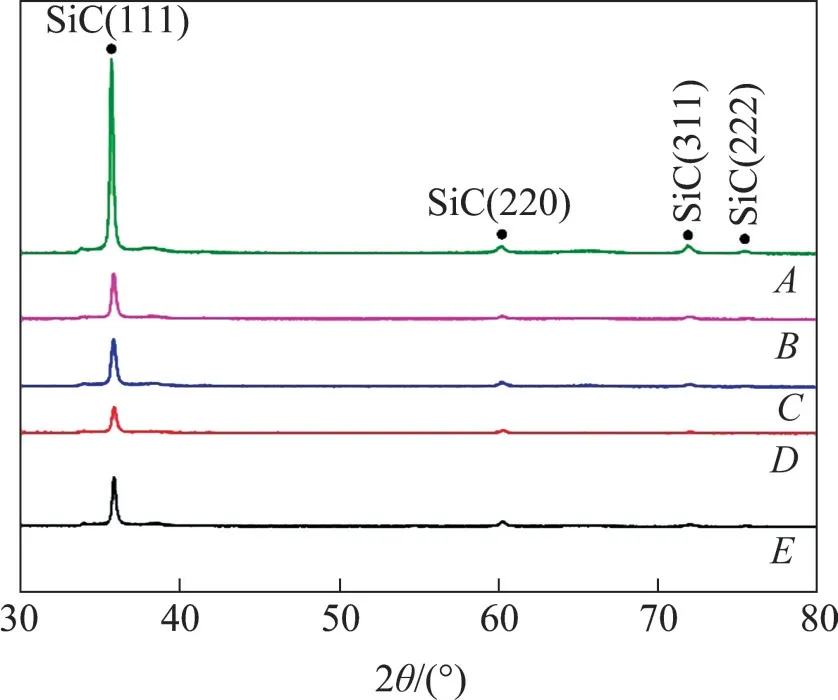
圖8 1 500 mm長CVD SiC涂層不同沉積位置的X射線衍射圖譜Fig.8 X-ray diffraction patterns of 1 500 mm long CVD SiC coatings at different deposition positions

圖9 1 500 mm長CVD SiC涂層不同沉積位置的SEM圖像Fig.9 SEM images of 1 500 mm-long CVD SiC coatings at different deposition positions

4 結論

1) 采用單因素試驗結合有限元仿真方法對CVD SiC 涂層工藝條件進行優化，獲得CVD SiC涂層的工藝參數水平如下：反應溫度為1 000 ℃左右，爐壓為400 Pa，Ar流量為1 200 mL/min，載氣H2流量為1 000 mL/min。SiC涂層的沉積速率在反應溫度為1 200 ℃出現明顯分界；當溫度低于1 200 ℃時，MTS 裂解生成SiC 主要由表面化學動力學控制；當溫度高于1 200 ℃時，反應主要由質量傳輸控制，此時，對于大長徑比的CVD SiC 涂層沉積均勻性影響較為嚴重；隨爐壓增大，SiC涂層沉積速率逐漸降低，并且SiC涂層沉積均勻性也隨之變差。隨載氣H2流量增加，SiC涂層沉積速率逐漸增大，在載氣H2流量為1 000～1 200 mL/min的條件下，SiC涂層沉積均勻性較好；隨基體數量增多，SiC涂層沉積均勻性隨之變差且沉積速率逐漸降低。

2) 在優化工藝條件下，得到沉積均勻性較好的β 型SiC 涂層，沉積均勻性的標準差Δ=2.172 38×10-7。沿反應氣體流動方向，SiC 涂層沉積速率逐漸降低，與有限元仿真結果一致，且平均相對誤差不大于8.3%，驗證了本文所建立有限元模型的正確性與可靠性。