MTLCDI控制連體超高層建筑風振響應研究

王欽華，吳華曉，田華睿，唐 意，賈 彬

（1.西南科技大學土木工程與建筑學院，四川綿陽 621010；2.汕頭大學土木與環境系，廣東汕頭 515063；3.中國建筑科學研究院有限公司，北京 100013；4.建筑安全與環境國家重點實驗室，北京 100013）

引 言

連體超高層結構作為一種復雜高層建筑類型，不僅擁有優美的建筑外觀、節省建筑所需的土地面積，而且各塔樓之間的連接體（如高空連廊）能提供開闊的觀光視野和獨特的視覺效果，因而其建筑形式得到廣泛應用［1］。按照塔樓與連接體的連接強弱可以分為柔性連接和剛性連接，柔性連接是指連接體可以通過隔振支座或者阻尼器等裝置與塔樓相連，柔性連接克服了剛性連接產生的端部應力復雜以及整體結構扭轉效應顯著等缺點［2?4］。因此，在工程中有廣泛的應用，如吉隆坡的雙子塔、北京當代MOMA、重慶來福士廣場等連體超高層建筑都采用柔性連接的形式。

目前，國內外學者針對剛性和柔性連接體超高層建筑在動力荷載作用下結構的響應進行了深入研究［5?7］。肖從真等［8］對北京麗澤SOHO 超高層雙塔連體結構的5 種連接方案進行抗震分析，最終選擇設置4 座連橋將雙塔“箍”成一個整體的方案。吳華曉等［9］建立了強、弱連接雙塔連體超高層風振響應分析的簡化數學模型，基于工程實例分析并對比了不同連接形式下的風振響應。研究表明：強連接形式可以減小兩棟建筑大多數風向角下的峰值加速度響應。Lee 等［10］分別研究了橡膠支座柔性和剛性連接對連體超高層建筑地震和風振響應的控制效果，研究表明：剛性連接在有些情況增加了結構的響應，而橡膠支座柔性連接能減小結構的動力響應。Xu等［11］進一步建立了基于阻尼器柔性連接連體超高層建筑在地震作用下的結構分析模型，并分析了在El Centro 地震作用下結構的響應，結果表明：優化的阻尼器能夠很好地控制連體建筑的地震響應。近幾年，基于慣容元件的阻尼器應用于控制建筑結構地震和風振響應的研究成為熱點［12?17］。該類阻尼器利用慣容元件機械原理實現表觀質量放大，可以在自身質量較小的情況下抑制超高層建筑的風振響應［18?20］。Palacios?Qui?onero 等［20］研究了TMDI 柔性連接的連體建筑在地震作用下的減震效果，結果表明：TMDI 比傳統的TMD 有更好的減震性能和魯棒性。本文作者分別對單及多調諧質量慣容阻尼器（TMDI，MTMDI）［21?23］用于單體及連體超高層建筑抗風和抗震進行研究，結果表明：基于慣容元件的阻尼器有更好的減振（震）性能。Wang 等［24］提出以建筑物的自帶水箱取代TMDI 中的質量塊，形成的單調諧液柱慣容阻尼器（TLCDI）不僅可以對主體結構振動響應進行控制，還可以發揮水箱日常用水和消防功能。文獻［25?26］將TLCDI 應用于連體超高層建筑抗震和抗風研究。通常，連體超高層建筑各個塔樓都有各自的水箱，各個水箱與慣容元件組成的多調諧液柱慣容阻尼器（MTLCDI）對連體超高層建筑風振響應的控制效果還需要進一步探索。而且，對上述4 種阻尼器（TMDI，MTMDI，TLCDI和MTLCDI）用于連體超高層建筑風振控制的效果缺乏系統的比較研究。

基于上述文獻分析，本文首先建立了MTLCDI控制連體超高層建筑風振響應非線性運動方程，并討論了其等效線性化方法的適用性；其次基于連體超高層建筑的風洞試驗獲得的風荷載時程，對MTLCDI 控制連體超高層建筑風致加速度、脈動位移響應和層間位移角進行分析；最后，比較了4 種阻尼器的控制效果，并對其進行討論。

1 數學模型及等效線性化方法的驗證

1.1 數學模型

在連體超高層建筑中安裝MTLCDI，如圖1（a）所示，該連體超高層建筑由B(1)和B(2)兩棟建筑組成，分別有i，j層。兩個連廊通過滑動支座分別與對應的TLCDI 連接，每個TLCDI 都包括U 型容器、容器內液體、彈簧元件、阻尼元件和慣容元件總共五個部分。容器的橫截面積、水平尺寸和質量分別為A，B，MC；液體總長度和密度分別為L和ρ=997 kg/m3，TLCDI 的總質量可記為mT=ρAL+MC。TLCDI 容器中間隔板水頭損失系數ξ取決于隔板的開孔率。為了比較MTLCDI 與其他阻尼器的減振效果，本文還討論了安裝TLCDI，MTMDI（如圖1（b）所示）以及TMDI 對連體超高層建筑的減振效果，未安裝振動控制裝置的原結構（OS）如圖1（c）所示。

圖1 連體超高層建筑結構示意圖Fig.1 Schematic diagrams of linked high-rise buildings

4 種減振方案僅考慮控制主體結構弱軸方向的響應，因此B(1)和B(2)可分別簡化成i和j個自由度的線性系統，MTLCDI 控制連體超高層建筑風致振動的運動微分方程為：

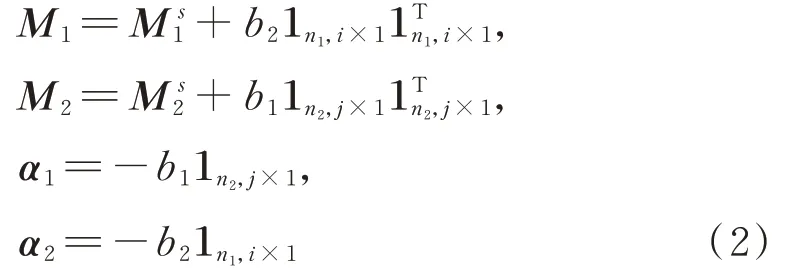
式中M1s∈Ri×i，M2s∈Rj×j分別為原結構B(1)和B(2)的質量矩陣，可由結構有限元分析模型獲得；1n1，i×1∈Ri×1表示第n1個元素等于1，其余元素為零的列向量，下文其余類似符號同義；b1和b2分別為慣容元件1 和2 的慣容系數；n1和n2分別表示慣容元件2 和1 相應的柔性連接固結點與B(1)和B(2)連接的層數；上標T 表示向量或矩陣的轉置運算符。在圖1（a）中，mT，1和mT，2分別表示TLCDI?1 和TLCDI?2總質量。

方程（1）剛度矩陣各項表示為：

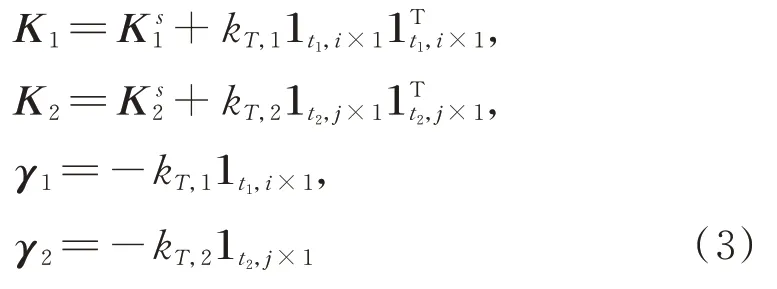
式中K1s∈Ri×i和K2s∈Rj×j分別為原結構B(1)和B(2)的剛度矩陣，可由結構有限元分析模型獲得；kT，1和kT，2分別為TLCDI?1 和TLCDI?2 的彈簧元件的剛度；t1和t2分別表示TLCDI?1 和TLCDI?2 彈簧和阻尼元件與B(1)和B(2)連接作用的層數。

方程（1）阻尼矩陣中各項可表示為：

式中cT，1和cT，2分別為TLCDI?1 和TLCDI?2 的阻尼元件阻尼，Cs1∈Ri×i為B(1)原阻尼矩陣，按下式［27］計算：

式中Φ1，ξ1，k和ω1，k分別為B(1)的模態矩陣、第k階阻尼比和自振頻率；φ1，k為B(1)第k階模態。同理，B(2)的阻尼矩陣C2s∈Rj×j參照式（5）。

在建立MTLCDI 控制連體超高層建筑的運動方程（1）后，TLCDI，MTMDI 和TMDI 控制連體建筑風致運動方程可由運動方程（1）退化獲得，例如：刪除方程（1）與MTLCDI 中液體自由度的對應行和列項；質量、剛度、阻尼矩陣與方程（2）～（5）表達一致，相關參數取MTMDI 對應的參數，即可獲得MTMDI 對應的運動方程。

式中為容器內液體速度(t)的標準差。

將式（6）代入式（1）得：

式（7）縮寫成：

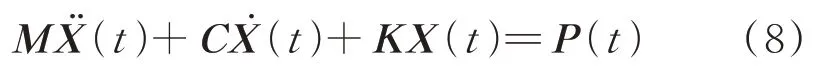
對式（8）等號兩邊進行傅里葉變換，MTLCDI控制超高層建筑位移和加速度響應頻響函數矩陣分別為［30］：

與TLCDI 控制系統相比，MTLCDI 非線性更強。因此，在文獻［26］的基礎上［26］，進一步驗證等效線性化方法對MTLCDI 控制系統的適用性。

1.2 等效線性化方法驗證

采用表1所給的優化參數，由數值方法求解非線性微分方程（1）和等效線性化后的方程（7），對比兩種方法的計算結果，驗證等效線性化方法的適用性。圖2是非線性方法和等效線性化方法計算的B(1)和B(2)頂層總體位移響應時程在90°風向角（橫風向）下的比較。

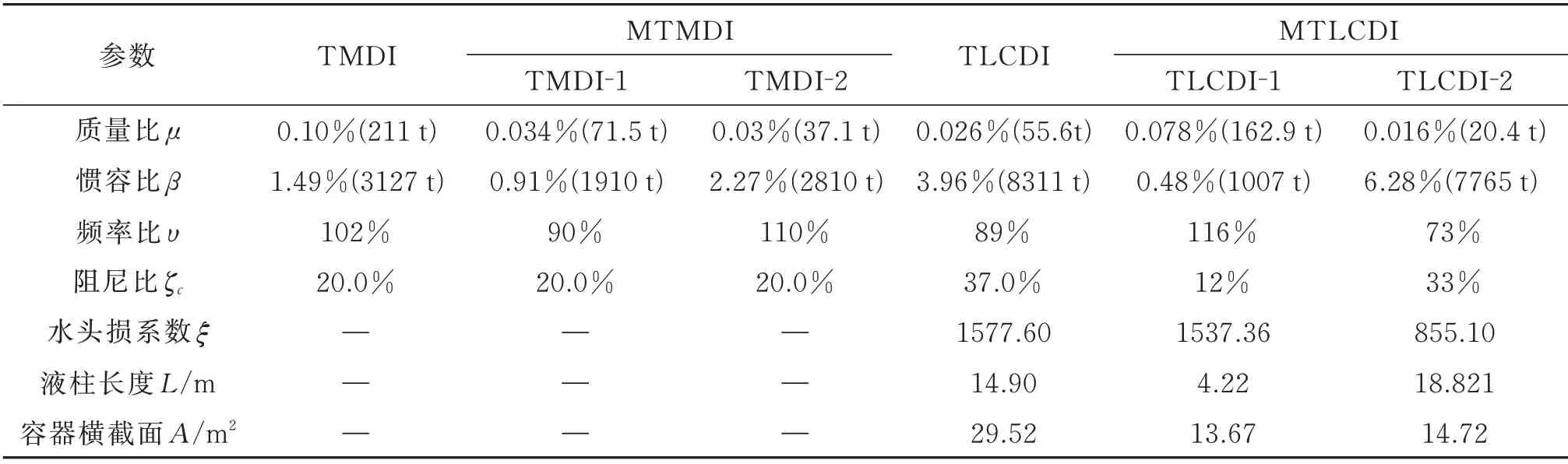
表1 四種慣容元件的阻尼器的最優參數Tab.1 Optimal parameters of four types of the inerter?based dampers

從圖2中可以看出兩種方法計算的總體位移時程響應幾乎一致。為了進一步比較這兩種方法的誤差，隨機選用MTLCDI 的100 組參數，計算兩種方法相對誤差的期望值δerr，其定義為［26］：

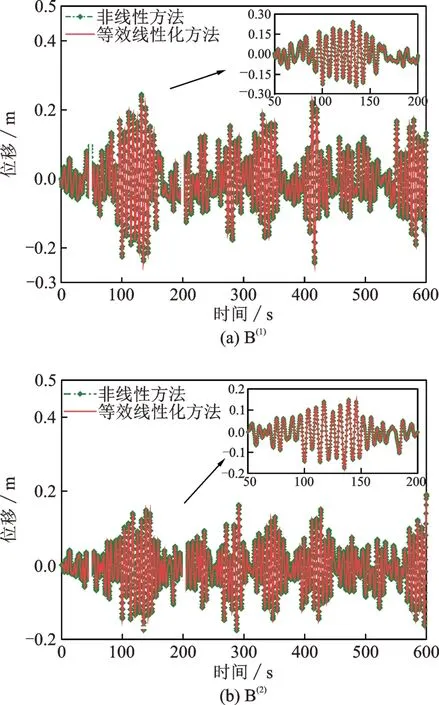
圖2 B(1 )和B(2 )的頂層位移時程在90°風向角下的比較Fig.2 Comparisons of the time histories of the displacement responses of the top storey of B( 1 )and B(2 )at 90° wind direction

式中δi為第i組參數兩種計算方法的相對誤差；分別為第i組參數下非線性方法和等效線性化方法計算的響應的標準差。表2給出了0°風向角（順風向）和90°風向角風致加速度和總體位移響應標準差的相對誤差的期望值。表2表明這兩種方法的計算結果相對誤差的期望值小于0.2%。根據圖2和表2的結果，證明了等效線性化方法求解MTLCDI 控制結構風致響應微分方程的適用性。

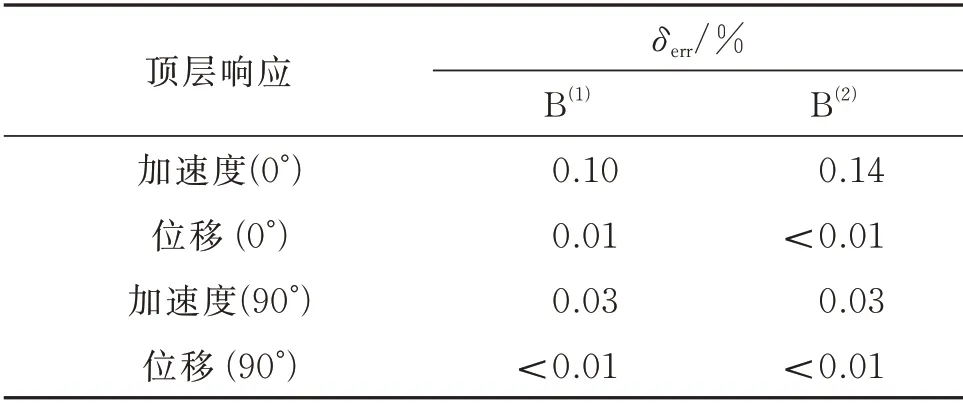
表2 0° 和90° 風向角下δerr 的值Tab.2 Values of δerr at wind directions of 0° and 90°

在驗證等效線性化方法的適用性后，可由式（7）獲得B(1)和B(2)的響應時程，其峰值響應定義為：

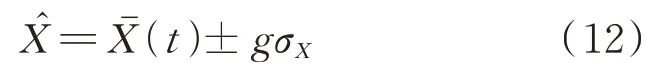
式中(t)和σX分別為選取樣本響應時程的期望和標準差，峰值因子g=3.0［31］。

2 工程實例分析

2.1 工程實例及其風洞試驗簡介

本文對位于中國東南沿海城市某連體超高層建筑進行了風致響應分析。該建筑的主要物理特征如下：B(1)和B(2)分別有59 層和55 層；總質量分別有209868 t 和123648 t。該連體建筑的平面圖和軸側圖分別如圖3（a）和（b）所示。圖3表明x軸是弱軸，結構最不利動力響應容易出現在水平側移剛度較弱的方向［22］，僅討論4 種裝置對x軸向的動力響應控制效果。

在汕頭大學風洞實驗室對B(1)和B(2)進行同步多點測壓風洞試驗，試驗模型比例采用1∶300。根據《建筑結構荷載規范》（GB 50009—2012）［32］，試驗模擬了B 類風場；初始風向角如圖3（a）所示，風向角沿逆時針方向間隔15°，從0°到345°共進行24 個風向角風洞試驗，風洞試驗相關信息詳見文獻［22?23］。

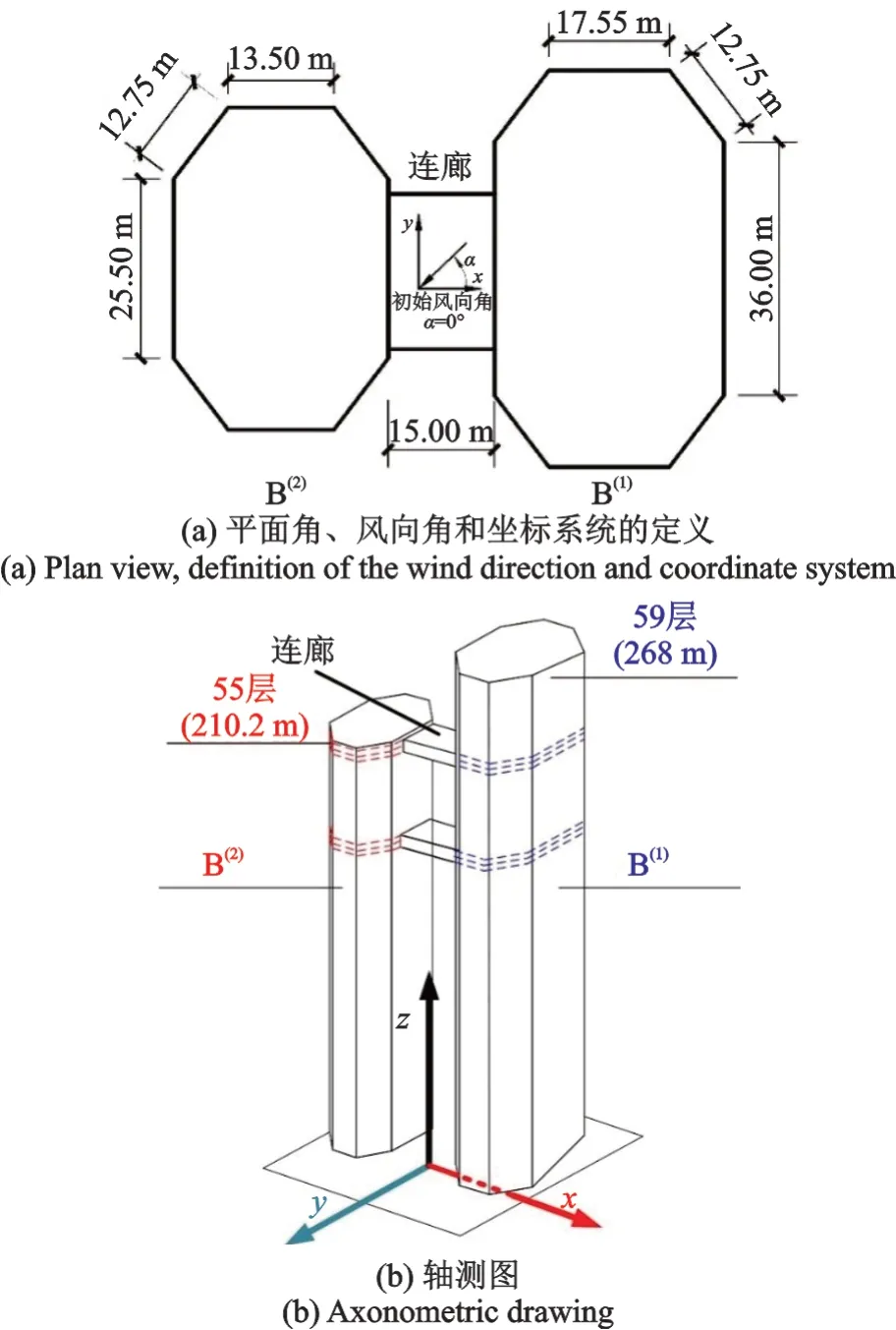
圖3 連體建筑示意圖Fig.3 Sketch of the linked buildings

2.2 四種基于慣容元件阻尼器的優化參數

在尋找最優MTLCDI 控制B(1)和B(2)風致響應過程中共有18 個待定參數，分別是TLCDI?h（h=1，2）的安裝樓層數、連廊連接樓層、質量比μh=MC，h/Mh（Mh是B(1)和B(2)總質量）、慣容比βh=bh/Mh、頻率比（ωT，h，ωs，h分別為TLCDI 的頻率及相應建筑的基頻）、阻尼比、水頭損失系數ξh、液柱總長度Lh和容器橫截面積Ah。其中安裝樓層數和連廊剛節點連接樓層數受限于結構的實際設計，其對應具體參數如下：TLCDI?1 安裝在B(1)的第46 層，對應連廊剛節點連接到B(2)的第55 層；TLCDI?2 安裝在B(2)的第53 層，對應連廊剛節點連接到B(1)的第44 層。余下參數的確定可視為帶約束多目標優化問題求解過程。對于超高層建筑，風致加速度往往是影響超高層建筑舒適度的最主要因素之一［33］，因此本文以B(1)和B(2)的加速度峰值和B(1)的位移標準差為3個優化目標。上述多目標優化問題的數學表達如下式：

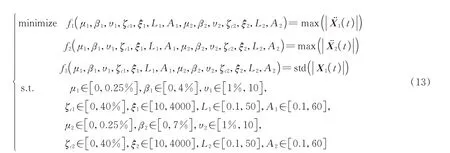
式中參數約束范圍的確定過程參考文獻［26］。使用MATLAB 內置函數‘gamultiobj’求解此多目標優化問題，將優化后的解集（最優個體的集合）繪制三維Pareto 前沿（如圖4所示）。基于點到面最遠距離的策略，在Pareto 前沿選擇膝點（knee point）作為MTLCDI 權衡3 個目標的最合適點。4 種控制方案選擇的最合適點對應參數列于表1。

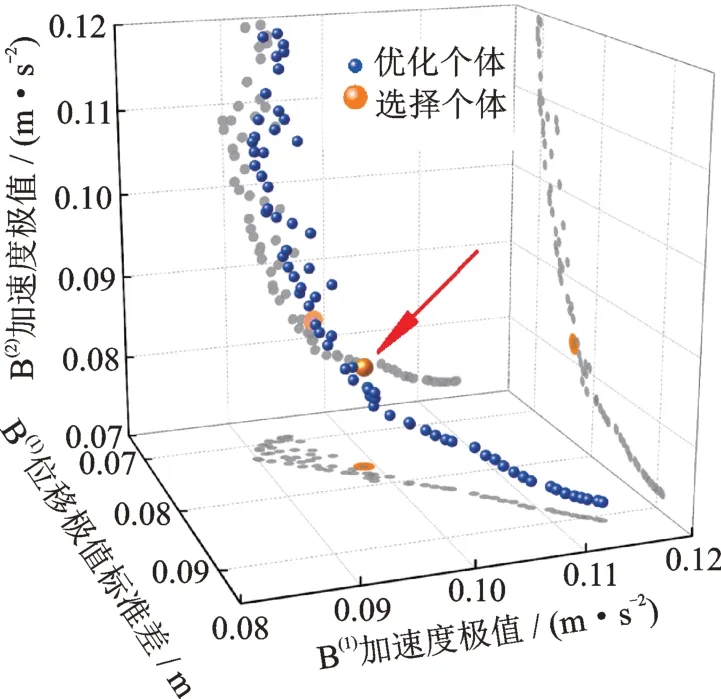
圖4 MTLCDI 最優個體的Pareto 前沿Fig.4 Pareto front corresponding to the parameter optimiza?tion of MTLCDI

2.3 風致加速度控制效果分析

本節分別討論了4 種控制裝置下連體超高層建筑加速度響應的頻響函數、時程及加速度響應峰值的減小效果。計算風致加速度響應時的風速為38.80 m/s（10年重現期），前3 階阻尼比取1.5%，其余階阻尼比的確定參見文獻［27］。根據式（10）計算了激勵力作用在B(1)和B(2)的頂層時，頂層的加速度響應的頻響函數。從圖5（a）可以看出，4 種方案都能明顯降低B(1)的加速度頻響函數在第1 階自振頻率附近的峰值，而MTLCDI 對其高階（第2，3 階）自振頻率附近的峰值也起到明顯的降低作用。圖5（b）表明4 種方案都能有效降低B(2)加速度頻響函數的前3 階固有頻率附近的峰值，且MTLCDI 對峰值的減小幅度優于其余控制方案。

圖5 頂層加速度響應頻響函數Fig.5 Frequency response function of the acceleration re?sponses of the top storey

根據式（7）可求得連體超高層建筑的風致加速度響應。圖6（a）和（b）分別給出了B(1)和B(2)頂層在270°風向角（橫風向）的加速度時程，圖6（a）和（b）表明4 種減振方案都能減小B(1)和B(2)的加速度響應，且對B(2)的控制效果更顯著。

圖6 270°風向角下頂層加速度響應時程Fig.6 Time histories of the acceleration responses of the top storey at 270°wind direction

獲得結構的加速度時程響應后，根據式（12）計算結構的加速度峰值響應。圖7（a）和（b）分別是B(1)和B(2)頂層風致加速度峰值隨風向角的變化情況。圖7（a）表明4 種減振方案都能大幅度降低B(1)在所有風向角下頂層的加速度的峰值，且控制效果基本一致。在沒有安裝控制裝置情況下，B(1)在90°和270°風向角下的加速度峰值最大，其數值約為0.16 m/s2，安裝MTLCDI 后在這兩個風向角下風致加速度峰值分別減至0.09 m/s2和0.10 m/s2。圖7（b）表明4 種方案均能顯著減小B(2)在所有風向角下的加速度響應，其中MTLCDI 減小幅度最大；在沒安裝控制裝置時，B(2)加速度峰值在0°（順風向）、90°和270°風向角下達到最大，其值接近0.18 m/s2，安裝MTLCDI 后在這3 個風向角下風致加速度峰值分別減至0.07，0.09，0.08 m/s2。

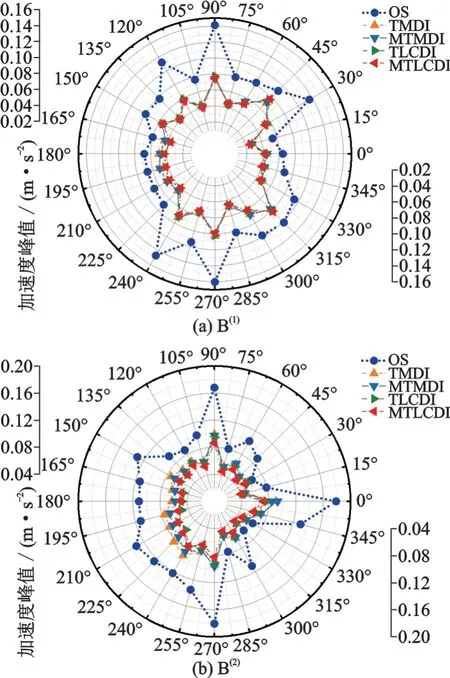
圖7 頂層風致加速度隨風向角變化Fig.7 Variations of peak wind?induced acceleration with wind directions from 0°to 345°

為了定量分析4 種控制方案的減振效果，定義了減振因子Fv：

式中ROS和RE分別表示連體超高層建筑安裝減振裝置前和后的響應峰值。由式（14）計算的B(1)和B(2)頂層加速度峰值在3 個典型風向角下的減振因子列于表3。表3表明4 種振動控制方案都能使B(1)和B(2)風致峰值加速度從無控制狀態的0.16 ～0.18 m/s2減小到0.09～0.10 m/s2，減振因子最大可達約60%。此外，對比3 個典型風向角下的B(1)和B(2)減振因子，4 種阻尼器對B(2)的峰值加速度控制效果優于對B(1)的控制效果。

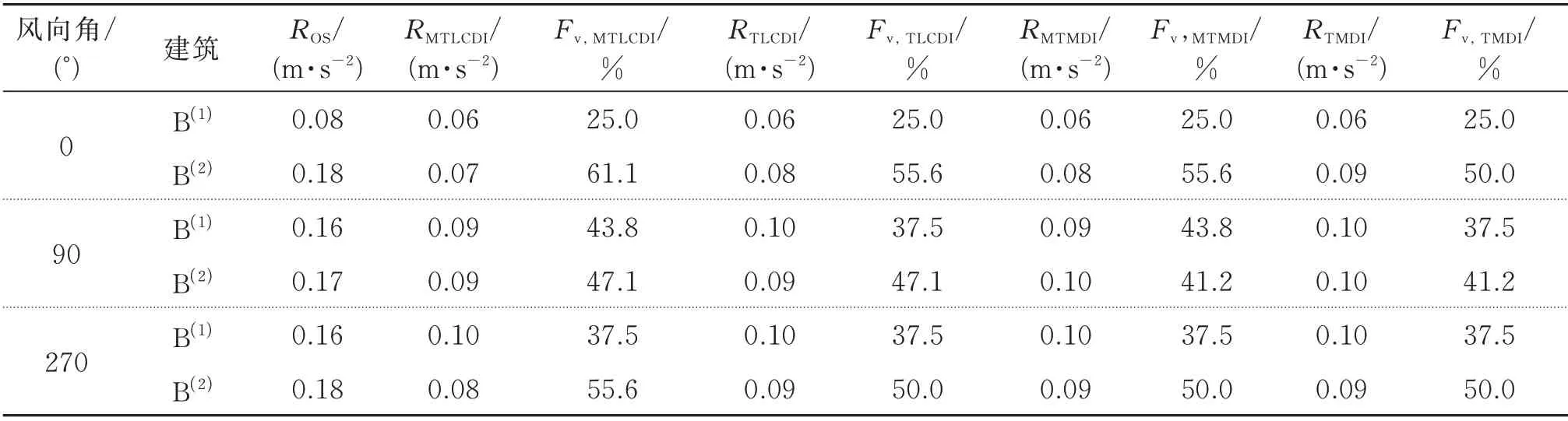
表3 典型風向角下B( 1 )和B( 2 )頂層風致加速度的減振因子Tab.3 Reduction factor of wind?induced acceleration of the top storey of B(1 )and B(2 )at typical wind directions

圖8（a）和（b）分別給出了連體超高層建筑在0°和270°風向角下峰值加速度沿樓層的變化規律。圖8表明4 種減振方案對B(1)和B(2)的各層的峰值加速度都能起到明顯的控制效果。在0°和270°風向角，MTLCDI 和TLCDI 對B(2)加速度控制效果相比于MTMDI 和TMDI 稍顯優勢，而對B(1)控制效果無明顯區別。

圖8 風致加速度峰值在0°和270°風向角沿樓層高度變化規律Fig.8 Variations of peak values of wind-induced acceleration with the height of buildings at 0° and 270° wind direc?tions

2.4 風致位移控制分析

本節分別討論了4 種控制裝置對B(1)和B(2)位移頻響函數、總體位移響應、脈動位移響應峰值和層間位移角的控制效果。位移計算前3 階阻尼比選取3%，其余階阻尼比與加速度分析時的一致，且計算B(1)和B(2)的風致位移響應時設計風速為50.8 m/s（50年重現期）。根據式（9），計算了激勵力作用在B(1)和B(2)的頂層時，頂層的位移頻響函數，如圖9所示。圖9（a）表明4 種控制方案僅對B(1)位移頻響函數在第1 階自振頻率對應的峰值有明顯降低作用，而對高階峰值減振效果并不明顯；圖9（b）表明4 種控制方案均能顯著減小B(2)前3 階自振頻率附近位移頻響函數的峰值，其中TLCDI 的效果最優。

圖9 頂層位移頻響函數Fig.9 Frequency response function of displacement of the top storey

根據式（7）計算出結構的風致總體位移響應。圖10（a）和（b）分別是30°風向角下（該風向角下的B(1)位移最大），B(1)和B(2)總體位移響應時程。圖10表明4 種方案都減小B(1)和B(2)的總體位移響應。

圖10 30°風向角下B(1 )頂層和B(2 )頂層總體位移響應時程Fig.10 Time histories of displacement responses of the top storey of B(1 )and B(2 )at 30°wind direction

風致總體位移響應由平均值和脈動部分組成，而被動控制裝置并不會對結構位移響應的平均值產生影響［18，23，27，34］，因此下面討論MTLCDI 對結構風致脈動位移響應的控制效果。由式（12）可得脈動位移響應部分峰值為gσX。

圖11（a）和（b）分別為B(1)和B(2)頂層脈動位移響應峰值隨24 個風向角的變化規律。圖11（a）表明4 種控制方案均能減小B(1)所有風向角下的脈動位移峰值，且控制效果接近。圖11（b）給出了B(2)位移脈動響應峰值隨風向角的變化規律。從圖11（b）中可以看出4 種控制方案能減小B(2)絕大部分風向角下脈動位移部分峰值，其中MTLCDI 略有優勢；但在部分風向角（如30°，120°，240°，330°）下，安裝減振設備后脈動位移峰值反而增大，這個現象出現的原因是安裝阻尼器設備的建筑通過連廊對另外一棟建筑施加了推力或者拉力，當B(2)的運動方向與推力或者拉力同向時，減振裝置起到了增大B(2)位移的作用［23］。

圖11 B(1 )和B(2 )頂層脈動位移峰值隨風向角變化Fig.11 Variations of peak values of wind-induced fluctuating displacement of the top storey of B(1 )and B(2 )at wind directions from 0°to 345°

脈動位移響應部分減振因子Fv同樣如式（14）所示。3 個典型風向角下，B(1)和B(2)頂層脈動位移響應峰值的減振因子如表4所示。在0°風向角，B(2)頂層減振因子在4 種控制方案中均大于30%，對應脈動位移峰值從0.20 m 減小到0.13 m；而B(1)減振系數僅有13%左右，對應脈動位移峰值從0.15 m 減小到0.13 m。在30°風向角，由于B(2)的未控制時的脈動位移很小（0.07 m），安裝控制裝置并通過彈簧、阻尼元件與B(1)連接后，受到B(1)的影響其位移響應反而增加了。在270°風向，B(1)的減振系數均接近于25%，對應頂層脈動位移峰值從0.32 m 減小到0.24 m。

表4 典型風向角下B( 1 )和B( 2 )頂層風致脈動位移部分峰值減振因子Tab.4 Reduction factor of peak values of wind-induced fluctuating displacement of the top storey of B( 1 )and B( 2 )at typical wind directions

圖12（a）和（b）分別給出了180（°順風向）和270°風向角下，連體建筑脈動位移響應峰值沿樓層高度的變化情況。圖12 表明在這兩個風向角下，4 種控制方案都能有效減小B(1)和B(2)各層的脈動位移峰值，且減振效果幾近一致。

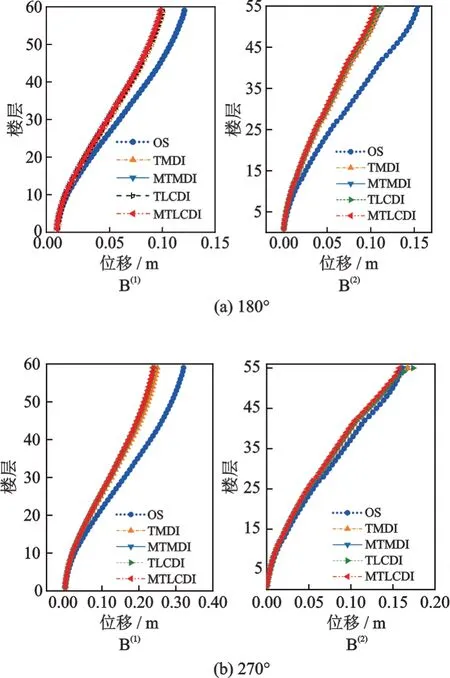
圖12 風致脈動位移峰值在180°和270°風向角沿樓層高度變化規律Fig.12 Variation of peak values of wind-induced fluctuating displacement with the height of buildings at 180° and 270°wind directions

為了避免建筑的位移響應過大影響結構的正常使用，《高層建筑混凝土結構技術規程》建議了其層間位移角的限值［35］。圖13（a）和（b）分別給出了180°和270°風向角下，連體建筑層間位移角沿樓層高度的變化情況。圖13 表明在這兩個風向角下，4 種控制方案都能有效減小B(1)和B(2)各層的層間位移角，使其幾乎都處于建議值1/500 以下，且控制效果幾近一致。

圖13 層間位移角在180°和270°風向角沿樓層高度變化規律Fig.13 Variation of storey drift ratio with the height of build?ings at 180°and 270°wind directions

3 結 論

本文建立了MTLCDI 控制連體超高層建筑的風致響應非線性數學模型，驗證了等效線性化方法的適用性，通過一個工程實例對MTLCDI 減振效果進行分析，并與其他3 種阻尼器的控制效果進行比較，得到以下結論。

（1）加速度響應方面：4 種振動控制方案都能大幅度減小B(1)和B(2)在24 個風向角下的加速度峰值響應，且對B(2)的控制效果較好，MTLCDI 的減振性能稍顯優勢，如在270°風向角，MTLCDI 使得B(1)頂層峰值加速度響應從0.16 m/s2降低到0.10 m/s2，對應減振因子為37.5%；B(2)峰值加速度響應從0.18 m/s2降低到0.08 m/s2，對應減振因子為55.6%。

（2）位移響應方面：4 種控制方案都能減少B(1)在所有風向角和B(2)在大部分風向角的下脈動位移響應部分峰值。同時，4 種控制方案在典型風向角下都能控制建筑的層間位移角，使其幾乎都滿足規程建議值。

總的來說，MTLCDI 比其他3 種基于慣容元件的阻尼器控制連體超高層建筑風致響應的控制效果略好，且MTLCDI 采用分布布置，節省了單個TLCDI 安裝空間和減小施工難度；此外，MTLCDI 系統中的液體部分在實際工程應用可被設計成消防水箱或游泳池等設施，兼具實用性和經濟性。