大跨懸索橋結構阻尼的風速依賴特性研究

郭增偉，時浩博，趙 林

（1.重慶交通科研設計院有限公司橋梁工程結構動力學國家重點實驗室，重慶 400067；2.重慶交通大學省部共建山區橋梁及隧道工程國家重點實驗室，重慶 400074）

引 言

千米級懸索橋剛度小、阻尼低的特點致使其容易發生各種形式的風致振動，跨徑排名前四的懸索橋均需要采用控制措施來克服風致振動以提高橋梁的抗風性能［1］，風荷載成為限制懸索橋跨徑進一步增大的最關鍵的控制荷載。懸索橋加勁梁屬于典型的鈍體斷面，空氣流經加勁梁斷面時會發生嚴重的氣流分離、再附現象，并在加勁梁表面產生周期性的壓力脈動，這種周期性壓力脈動在影響結構振動狀態的同時，也受到結構振動狀態的影響，這就是橋梁風致振動區別于其他振動形式的“氣動彈性”效應，氣彈效應的存在將導致結構自振頻率和阻尼依賴于風速［2?3］，因此不同風速下結構自振頻率和阻尼的實測對氣彈效應的研究至關重要。另外結構固有頻率和阻尼也是振動控制的關鍵［4］，充分了解懸索橋自振頻率和阻尼隨風速的變化規律對懸索橋風致振動特性及其控制措施的研究有非常重要的參考價值。

目前常用的結構模態參數識別方法主要有：環境激勵法和強迫振動法。環境激勵法（Natural Exci?tation Technique，NExT）無需人工激勵和大型器械、不影響結構正常使用且識別結果也相對準確，在大型結構的模態識別中應用更為廣泛。1997年Pe?terson 等［5］首先將環境激勵法引入土木工程領域，用特征系統實現算法（Eigensystem Realization Algo?rithm，ERA）準確識別一個4 層框架結構的自振頻率，開創了環境激勵法識別結構模態的先河。2006年，Huang 等［6］首先把希爾伯特?黃變換應用于鐵路橋的健康監測中，準確識別了該橋的模態頻率和模態阻尼，證明了基于環境激勵的模態參數識別方法在實際工程中運用的可行性。2008年，日本東京大學Siringoringo 等［7］利用特征系統實現算法對多座橋梁進行了連續觀測和參數識別，準確識別了Hakucho 橋的前5 階模態頻率，證明了環境激勵法在不同種類橋梁中的普適性。2011年，姜浩等［8］利用NExT?ERA 方法識別了在地震激勵下某座預應力混凝土連續梁橋的前4 階豎向模態頻率和模態阻尼比，發現該方法的模態頻率識別結果與有限元計算結果具有良好的吻合性，模態阻尼比存在較大的誤差。同年，張艷輝等［9］利用隨機減量法識別出了風載激勵下某剛構橋的模態頻率和模態阻尼比，發現模態阻尼比的識別結果與有限元計算結果存在較大的誤差，推測原因是風速對阻尼的影響。2016年，Wang 等［10］用小波變換的方法準確識別了蘇通大橋在臺風下的前4 階豎向、前2 階扭轉和第1 階水平方向的各22 組模態頻率和模態阻尼比，探討了蘇通大橋的模態參數隨時間的演化規律和風速對模態頻率、模態阻尼比的影響，但因受到實測數據量的限制，并未論述識別結果的統計特征。2017～2018年，韓國首爾大學Kim 等［11?3］采用NExT?ERA 方法，基于Jindo 橋渦激振動實測數據系統研究了安裝了多重調諧質量阻尼器后的橋梁模態和未安裝阻尼器前該橋模態阻尼的變化情況，通過引入AM 函數穩定車輛荷載響應數據，并排除其他環境因素（如振動水平、溫度和風速）的影響，識別出了與振幅具有線性依賴特性的阻尼比，其用95 組數據闡述了環境因素對阻尼比存在影響，但并沒有對模態阻尼比在各種環境下的變化規律展開深入研究。

雖然環境激勵法能較為準確地識別得到的結構自振頻率，但受自然環境、車輛的影響，結構阻尼比的識別結果離散性較大；另外目前對結構自振參數的識別結果多是從確定性的角度加以描述，少有人從統計的角度考察模態阻尼隨風速的變化規律。本文選取了為期一年的西堠門大橋風速和加速度響應實測數據，使用NExT?ERA 方法識別并分析了不同風速條件下西堠門大橋模態參數，討論了模態阻尼比識別結果的分布規律和概型分布，最后給出了模態阻尼比隨風速變化的置信區間。

1 結構模態識別NExT-ERA 方法

NExT?ERA 法是將自然環境激勵技術和特征系統實現算法相結合的一種模態識別方法［14］。該方法首先對環境激勵下結構的響應加速度數據（輸出）進行預處理，并用計算得到結構的互相關函數代替脈沖響應函數，再對由脈沖響應函數構成的Hankel矩陣進行奇異值分解，得到系統的最小實現，從而得到系統矩陣，并據此求解出系統的模態頻率和模態阻尼。NExT?ERA 方法計算效率高，對復雜的結構系統具有較強的識別能力，適用多種結構的模態識別。

用不同測點之間響應加速度的互相關函數代替傳統時域模態辨識法中的自由振動響應或脈沖響應函數是NExT 方法最核心的貢獻。當動力系統的k點受到單位脈沖的激勵時，系統i點的脈沖響應hir（t）可表示為：

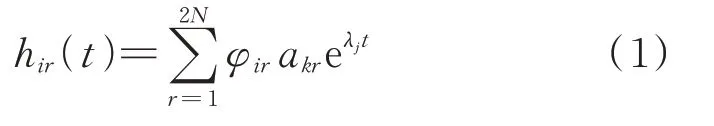
式中φir為第i測點的第r階模態振型；akr為僅同激勵點k和模態振型r有關系的常數項。

當系統k點在環境激勵fk（t）作用下，系統i點和j點的響應分別是xik（t）和xjk（t），當環境激勵fk（t）為白噪聲時，這兩者之間的互相關函數可以寫為：

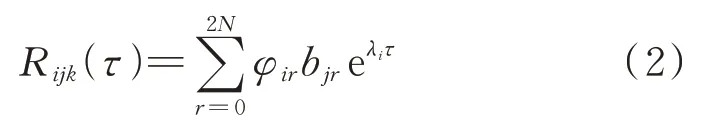
式中bjr為僅與參考點j及模態階次r有關的常數項。

對比式（1）和（2）可以發現，在白噪聲激勵下，線性系統中任意兩點的互相關函數與動力系統的脈沖響應函數除了常數項不一致外，兩者函數形式完全一致，而當各測點的同階模態振型乘以一個常數時，并不改變模態振型形狀，因此用互相關函數代替脈沖響應函數的做法可用于模態參數識別中。

ERA 法的基本思想是用脈沖響應函數構造Hankel 矩陣，并對其進行奇異值分解得到系統的最小實現并求得系統矩陣A，最后求解系統矩陣A的特征值和特征向量得到系統的模態參數。廣義Hankel 矩陣可以利用動態系統的脈沖響應函數h（k）進行構造［15］：

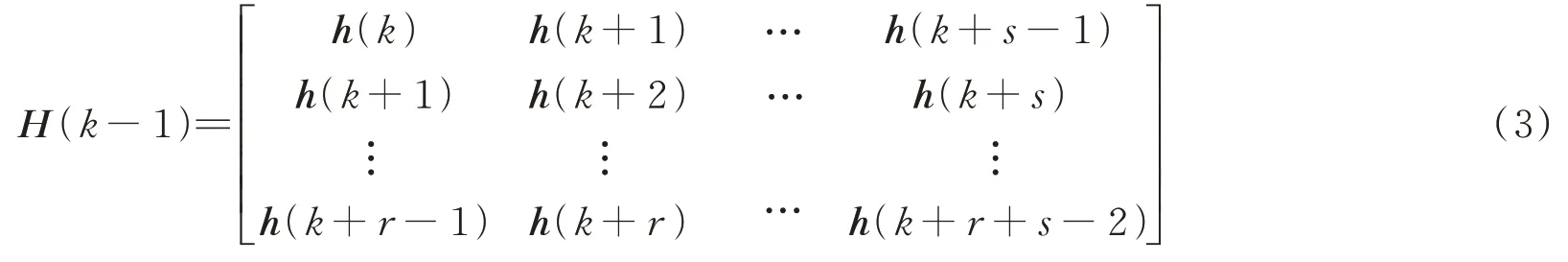
式中r=1，2，3，…；s=1，2，3，…矩陣中的每一個元素均為L×P維矩陣。

當k=1 時，對H（0）進行奇異值分解后，即可得到系統的最小實現：

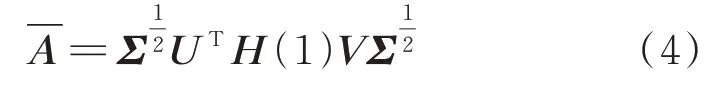
式中U，V和Σ分別為H（0）奇異值分解后的上三角、下三角和對角矩陣，而系統矩陣的特征值和特征向量即為系統的模態參數。

2 實測數據的預處理和模態識別結果準確性驗證

2.1 實測結果的預處理

西堠門大橋是中國浙江省舟山市境內的跨海大橋，橋位屬于典型的A 類地貌，主梁設計基準風速為55.1 m/s。橋位處風速序列利用如圖1所示的安裝于主跨1/4，1/2，3/4 跨徑處距離橋面5 m 的燈柱上的6 個Wind Master Pro 超聲風速儀收集得到（每個截面2 個風速儀），即采集的是距離海平面62.6 m處的風速；加勁梁加速度響應時間序列利用安裝于主跨1/4，1/2，3/4 位置和邊跨1/2 位置處的12 個加速度傳感器收集得到（每個截面2 個豎向加速度計、1 個橫向加速度計）；超聲風速儀的采樣頻率為32 Hz，加速度傳感器采樣頻率為50 Hz。

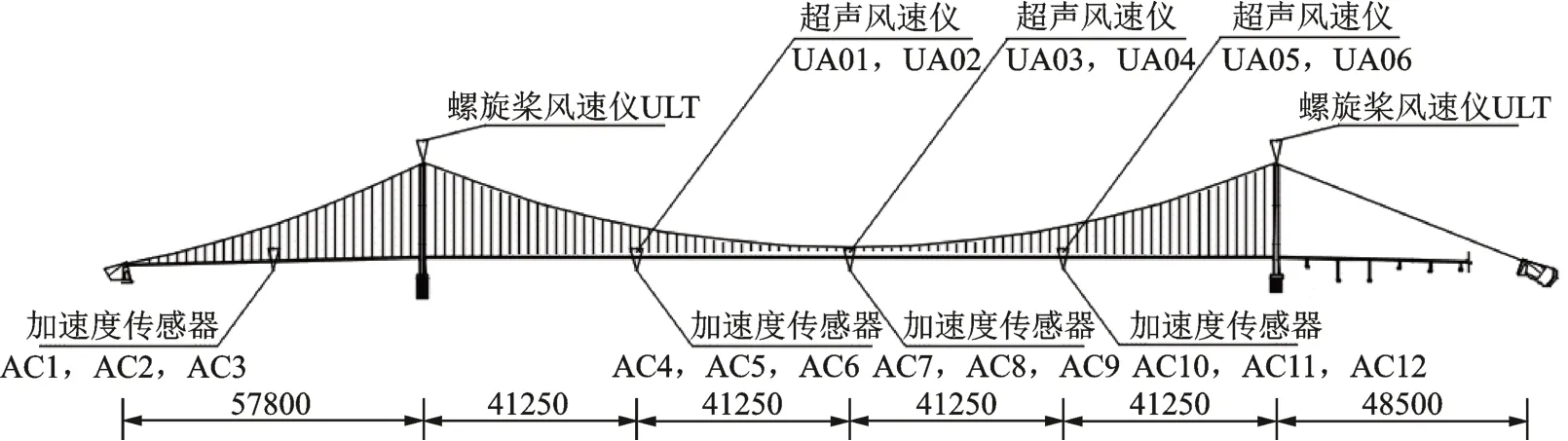
圖1 西堠門大橋風速儀和加速度傳感器總體布置圖（單位：cm）Fig.1 Layout of the anemometers and acceleration absorbers installed on the Xihoumen Bridge（Unit：cm）

選用西堠門大橋2012年全年實測風速及響應加速度數據作為識別西堠門大橋模態的原始數據。由于風速儀和加速度計長期在潮濕環境下工作壽命縮短、在低溫惡劣環境下工作易失靈、在雷暴天氣下風向標易損壞、在強風天氣下線路易中斷等現場復雜環境的影響，上述數據中會出現一些壞點或沒有數據的點，因此模態識別處理數據之前需要先剔除原始數據中一些存在明顯錯誤的風速和加速度壞點，即采用萊茵達（PauTa）準則將實測風速和加速度時間序列中大于3 倍標準差的瞬時值予以清除［16］。另外，日常運營過程中加勁梁的加速度響應實際上是橋梁在車輛、風、溫度等多種復雜動力荷載作用下的復合響應（輸出）結果。因此，為盡量規避車輛、溫度、風向對橋梁自振模態參數的影響，本文對實測風速與加速度數據進行了進一步的篩選。經調查發現，西堠門大橋在夜間車輛通行量遠小于日間，且夜間溫度相對比較穩定，故選擇用于模態識別的輸入與輸出數據皆為從23：00 至次日早晨6：00 區段內風速與加速度數據；另外在挑選數據時段時，還限定10 min 平均風速在連續1 h 內波動不超過10%、10 min 平均風向與橋軸線方向的夾角在±60°范圍內。

為了探究西堠門大橋自振頻率和氣動阻尼隨風速的變化規律，分別從1年的監測數據中遴選了如表1所示的0，2.5，5，7.5，10，12.5 和15 m/s 七組風速條件下的共計3015 組三向加速度數據，其中每組數據都為實測夜間連續1 h 內的加速度數據，則每組內共包含25×3600=90000 個加速度數據。

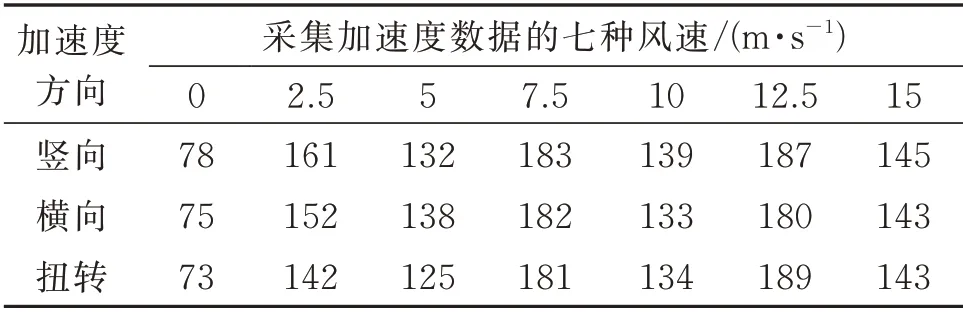
表1 七種風速條件下三向加速數據的采集組數Tab.1 Amount of acceleration samples at different wind speeds

2.2 模態識別結果的準確性驗證

為驗證使用NExT?ERA 方法識別的西堠門大橋模態結果的準確性和可靠性，選取無風環境中226 組西堠門大橋的前3 階豎向、橫向和扭轉的模態頻率和模態阻尼識別結果，并與ANSYS 有限元模型的計算結果以及譚慶才［17］于2012年利用強迫振動試驗實測的西堠門大橋固有模態結果進行了對比，結果如表2所示。從表中可以看出，NExT?ERA方法識別得到的主梁豎向、橫向及扭轉的模態頻率均值與有限元計算結果和強迫振動試驗結果吻合良好，識別誤差均在0.4%以內，且226 組振動樣本頻率識別結果的變異系數不超過0.05；雖然226 組樣本的模態阻尼均值也均在現場強迫振動試驗給定的范圍內，但利用不同振動樣本時間序列識別得到的模態阻尼波動明顯，扭轉阻尼的變異系數接近于1.0；橫向和扭轉阻尼比大致相當，但豎向振動阻尼比均值僅為橫向和扭轉阻尼的40%左右，在統計意義上與橫向和扭轉阻尼比的差異顯著。總體而言，使用NExT?ERA 方法能較為準確、可靠地識別西堠門大橋的模態參數。

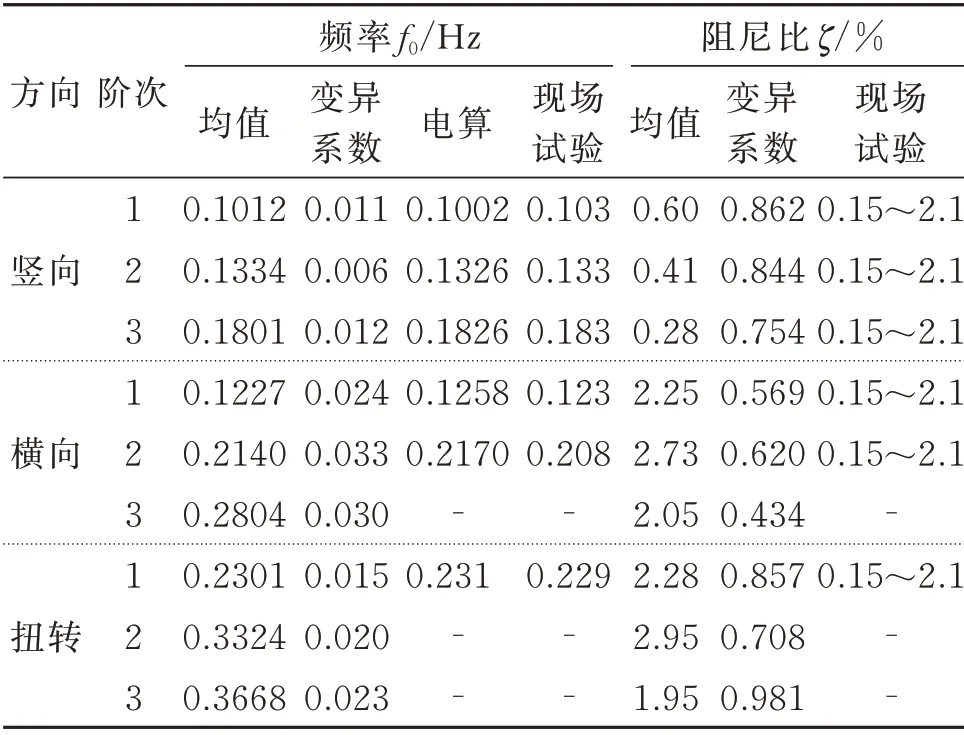
表2 模態識別結果與電算及振動試驗結果的對比Tab.2 Comparison of the identification results obtained by different methods

需要特別說的是，NExT?ERA 模態參數方法中時間序列的總長度、采樣頻率和Hankel 矩陣維數的取值會影響到互相關函數的質量，經過多次嘗試，最終發現用于西堠門大橋模態參數識別的樣本總時長不宜小于結構基本周期的120 倍，采樣頻率不宜低于25 Hz，Hankel 矩陣的維數不宜低于340，權衡計算成本后，確定上述3 個參數的取值分別為：60 min，25 Hz，340。

3 模態阻尼隨風速的變化規律

利用經過預處理的0，2.5，5，7.5，10，12.5 和15 m/s 七組風速條件下的共3015 組三向加速度時程樣本數據進行結構模態參數識別，為形象說明不同樣本序列識別結果的波動性，圖2給出了平均風速為2.5 m/s 時，455 組利用主梁加速度數據識別得到的西堠門大橋豎向、橫向及扭轉模態頻率和模態阻尼。

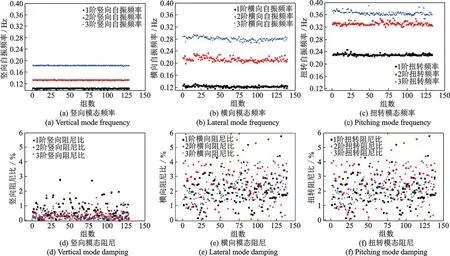
圖2 風速2.5 m/s 下豎向、橫向及扭轉模態頻率和阻尼比的識別結果Fig.2 Identification results of modal frequency and damping ratio in vertical，lateral and pitching direction at the wind speed of 2.5 m/s

從圖中可以看出，NExT?ERA 方法具有穩定的頻率識別能力，基于455 組主梁振動加速度時程序列識別得到的西堠門大橋主梁豎向、橫向和扭轉三個方向的前3 階自振頻率受樣本序列的影響較小，相對而言豎向和扭轉頻率受樣本影響的波動略低于橫向振動頻率；然而，利用不同樣本序列獲得的豎向、橫向、扭轉三個方向的阻尼識別結果則波動明顯，且扭轉阻尼比受振動樣本時間序列的影響最大、橫向阻尼比次之、豎向阻尼比最小。阻尼比受加勁梁加速度時間序列樣本顯著變化的現象說明從統計的角度描述結構阻尼隨風速的變化規律更為科學、準確。

3.1 不同風速下三向模態阻尼識別結果

七組風速下使用不同加速度時間序列獲得的結構模態阻尼均呈現出波動的特征，而氣動阻尼的風速依賴特性必然造成結構模態阻尼的波動程度、范圍也各不相同。為了探究結構模態阻尼的分布區間、波動程度與風速的依賴關系，圖3給出了七組風速下結構豎向、橫向及扭轉模態阻尼隨風速變化的箱型圖。從圖中不難看出：總體上相同風速條件下結構扭轉和橫向振動阻尼的均值和方差均大于豎向振動阻尼，但隨著風速的增大，這種差異將逐漸減弱；從均值上看，結構豎向模態阻尼隨風速的增大而增大，扭轉阻尼則隨風速的增大略有下降，而橫向模態阻尼受風速影響不大；從離散性上看，豎向振動模態的離散程度隨風速的增大而增大，扭轉阻尼的離散程度隨風速的增大略有下降，而橫向振動模態阻尼的離散程度則基本不受風速變化的影響。

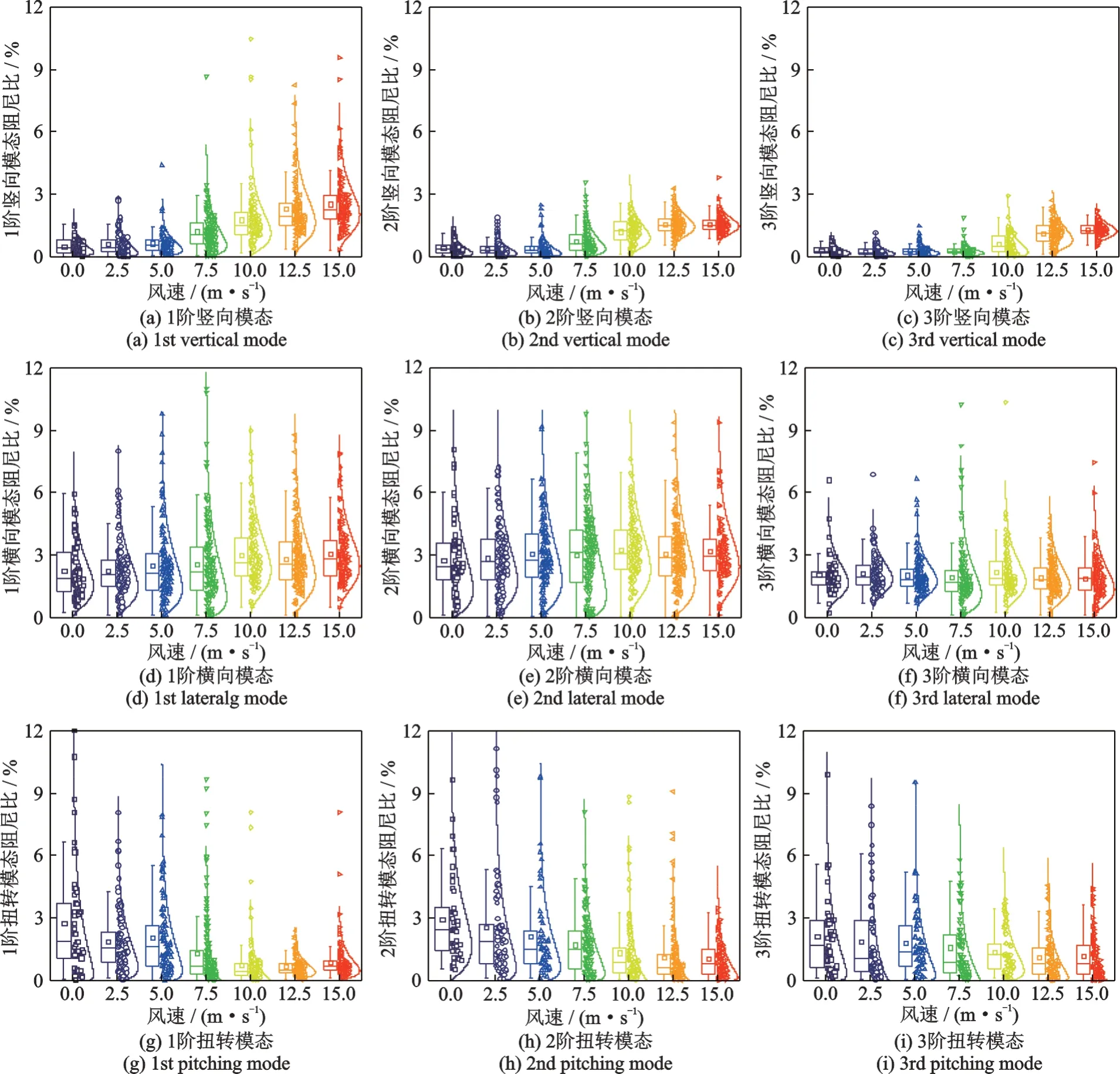
圖3 豎向、橫向和扭轉的模態阻尼比隨風速變化的箱型圖Fig.3 Box diagram of modal damping ratio in vertical，lateral and pitching direction at different wind speed

大量的風洞試驗和理論分析［18］表明：當氣流流經橋梁斷面時，空氣與主梁的氣動耦合產生的自激氣動升力與加勁梁振動位移相位差在180°左右，產生了隨風速增大而增大的正氣動阻尼，正氣動阻尼與結構自身阻尼疊加后將導致橋梁整體的豎向模態阻尼隨風速增大而增大的現象；但是氣動自激升力矩的方向與加勁梁振動位移之間相位差在0°左右，產生了隨風速增大而增大的負氣動阻尼，負氣動阻尼與結構自身阻尼疊加后將導致橋梁整體的豎向模態阻尼隨風速增大而降低的現象。本文使用NExT?ERA 模態識別算法得到的阻尼隨風速的變化趨勢與上述理論分析結果一致，證實了本文結果的正確性。

3.2 模態阻尼分布的概型分布

三個方向阻尼比的識別結果都表現出一定的隨機性和離散性，隨機變量的概型分布是描述其統計特性的最重要指標之一，而400 多組的加速度時間序列的識別結果也為結構阻尼比概型分布的研究提供了數據基礎。

概型分布的檢驗方法主要有：卡方檢驗、蒙特卡洛法、K?S 檢驗法。K?S 檢驗法一般使用p值（原假設下觀察到的檢驗統計量等于或大于觀測值的概率）來評價樣本數據分布與理論分布的相似性，進而確定隨機變量的概率分布類型，p值越接近0，表示拒絕原假設的統計學依據越充分，p值越接近1，表示接受原假設的統計學依據越充分。使用K?S 檢驗法計算不同風速下各階模態阻尼在廣義極值分布假設條件下的p值，在與0.05 檢驗水平下觀測值概率對比后，發現不同風速下各階模態阻尼比不拒絕服從廣義極值分布。

圖4給出了用廣義極值分布的概率密度函數（PDF）對在6 種風速條件下1 階豎彎模態阻尼的擬合結果。從圖中可以看出，廣義極值分布能很好地擬合各風速下結構的豎彎模態阻尼；隨著風速的增大，1 階豎彎阻尼比的分布形狀發生了從“矮胖”到“瘦高”的明顯變化，到風速為12.5 m/s 時，1 階豎彎阻尼比的分布形狀最為“瘦高”，即豎彎阻尼比識別結果的離散性最小，當風速繼續增大到15 m/s時，1 階豎彎阻尼比的分布形狀又變得稍“矮胖”，即此時的豎彎阻尼比識別結果的離散性又逐漸增大了。

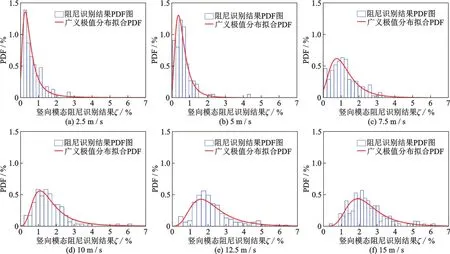
圖4 各風速下1 階豎彎阻尼識別結果的PDF 擬合結果Fig.4 Fitting results of damping ratio of 1st vertical mode at different wind speed

廣義極值分布是三種極值分布的廣義函數，形狀參數γ決定了極值分布的類型。當γ=0 時，廣義極值分布退化為尾部呈指數下降的極值Ⅰ型分布；當γ>0 時，廣義極值分布退化為尾部呈多項式下降的極值Ⅱ型分布；當γ<0 時，廣義極值分布退化為尾部有限的極值Ⅲ型分布。位置參數μ反映了極值分布的均值，尺度參數σ反映了極值分布的方差。為了進一步探究不同風速下的三個方向阻尼比的概率分布，圖5給出了三個方向前3 階阻尼比廣義極值分布的形狀函數γ隨風速的變化。從圖中可以看出：總體而言，雖然扭轉振型阻尼的概型分布并不隨風速變化（始終為極值Ⅱ型分布），但其形狀函數γ隨風速的明顯波動表明扭轉振型阻尼的分布形狀受風速影響明顯；橫向振型阻尼的形狀參數γ隨風速波動較小，表明其概型分布受風速的影響不大；豎向振型阻尼的形狀參數γ隨風速波動明顯且發生符號改變，表明其概型分布受風速影響較大。具體而言，1 階豎向阻尼比分布的形狀參數γ均大于0，說明1階豎向模態阻尼比均服從極值Ⅱ型分布，2 階和3 階豎向阻尼比分布的形狀參數在低風速下大于零、而在高風速下小于零，表明2 階和3 階豎向阻尼比的分布在低風速下服從極值Ⅱ型分布、在高風速下服從極值III 型分布；1 階橫向模態阻尼比均服從極值Ⅱ型分布，2 階橫向阻尼比服從極值Ⅲ型分布，3 階橫向阻尼比的分布在低風速下服從極值Ⅱ型分布，在高風速下服從極值Ⅲ型分布，前3 階扭轉模態阻尼比均服從極值Ⅱ型分布。

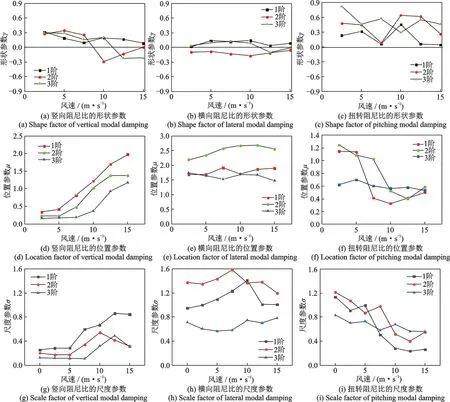
圖5 模態阻尼比廣義極值分布中特征參數隨風速的變化Fig.5 GEV distribution parameters of mode damping ratio at different wind speed

另外，從位置參數μ（均值）和尺度參數σ（標準差）隨風速的變化趨勢可以看出，豎向阻尼的均值和標準差隨風速的增大而增大，扭轉阻尼的均值和標準差則隨風速的增大而減小，而橫向阻尼的均值和標準差受風速的影響并不顯著。

3.3 模態阻尼隨風速演化的置信區間

對不同風速條件下三個方向前3 階結構模態阻尼的概率密度函數進行擬合，即可得到各工況下結構模態阻尼比的概型分布特征參數，據此便可獲得各工況下結構模態阻尼比在不同保證率下的置信區間。圖6給出了95%的置信水平下，三個方向前3階結構模態阻尼比的置信區間隨風速的變化情況。

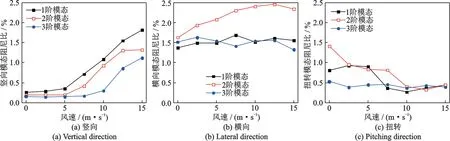
圖6 不同風速下的95%置信水平的模態阻尼比下限Fig.6 Lower limit of modal damping ratio at different wind speed in 95% confidence level

總體而言，西堠門大橋的阻尼比相對較低，在95%的保證率下，前3 階豎向阻尼比的分布區間為0.2%～2.1%，前3 階橫向阻尼比的分布區間為1.3%～2.8%，前3 階扭轉阻尼比的分布區間為0.3%～2.3%。從圖6（a）中可以更為明顯的看出，當風速低于7.5 m/s 時，前3 階豎向阻尼比受風速的影響并不十分顯著，但風速超過7.5 m/s 后，前3 階豎向阻尼比將隨風速的增大明顯增大，且阻尼比置信區間的寬度也隨風速的增大逐漸增大；3 階豎向振型的阻尼比在風速達到10 m/s 后才隨風速顯著增加，這表明低階豎向振型的阻尼比相對于高階振型更容易受風速的影響。從圖6（b）中可以明顯看出，1 階和3 階橫向阻尼比隨風速增大表現出在某一平衡位置上下波動的趨勢，2 階橫向阻尼比隨風速增大表現為緩慢增大的趨勢，但風速的變化對各階橫向阻尼比的大小及離散性的影響都較小。從圖6（c）中可以明顯看出，3 階扭轉阻尼隨風速的增大都呈現下降趨勢，且置信區間寬度逐漸變窄，與豎向振動阻尼相反，當風速低于7.5 m/s 時，各階扭轉振型阻尼受風速影響較大，而風速超過7.5 m/s 扭轉阻尼受風速影響逐漸減弱，相對而言低階扭轉振型阻尼受風速的變化更為敏感。

4 結 論

以西堠門大橋的實際工程背景、基于現場采集風速和加速度數據，識別了不同風速條件下共3015組三向加速度數據對應的模態參數，重點討論了結構模態阻尼隨風速的變化規律，分析了模態阻尼比的概型分布及其置信區間，得到如下結論：

（1）西堠門大橋的三向模態參數識別結果與有限元模態分析以及現場振動試驗結果相吻合，NExT?ERA 方法可以高效準確的識別西堠門大橋的模態參數；

（2）不同風速下西堠門大橋橫向振動阻尼比均在1.0%以上，但特定風速下結構豎向和扭轉振動阻尼在95%保證率的最小值分別為0.2%和0.3%，僅為設計建議值0.5%的一半，抗風設計和風洞試驗時應該引起足夠的重視；

（3）隨著風速的增大，結構豎向振型阻尼的均值和方差總體呈上升趨勢，扭轉振型阻尼的均值和方差總體呈減小趨勢，橫向振型的均值和方差受風速的影響不大。

（4）不同風速條件下西堠門大橋三個方向的模態阻尼比不拒絕服從廣義極值分布，但風速會影響結構豎向和扭轉振型阻尼的概型分布的拖尾性質。