山脈地形迎風面輸電線路風偏響應特性

劉春城，孫紅運

（東北電力大學建筑工程學院，吉林吉林 132012）

引 言

中國的地理位置和地形特點導致很多輸電線路架設在山區環境中。受山體的影響，山地風場與大氣邊界層風場存在很大差異。在山脈迎風面，由于山體的阻擋，會導致來流風的橫向風速顯著減小，使線路風偏減小，對線路風偏有利。但是由于爬坡加速效應，又會產生很大的上升氣流，豎向風速顯著增大，會對輸電線路風偏產生不利影響。在橫向風和豎向風的共同作用下，迎風面處輸電線路風偏特性及計算方法與平地有很大差別。影響這種差別的主要因素包括線路架設位置、桿塔呼稱高、山脈坡度。

目前國內外學者大多數關于輸電線路風偏響應的研究都基于平坦地貌邊界層風場［1?4］。De Bray 利用風洞試驗的方法對單山坡地形下的越山風效應進行了研究，針對陡坡和緩坡兩種情況研究了坡度對風場特性的影響［5］。Bowen 等、Lubitz 等、Neff 等研究了山體坡度、風向角、山體粗糙度等因素對加速效應的影響，但山體模型都是比較簡單的山丘，并未考慮山體長度［6?8］。張宏杰等則針對由兩個軸對稱山丘組成的峽谷地貌進行了一系列風洞試驗，得出了山脊和峽谷中軸線上風剖面的分布規律，并給出了典型位置處的計算公式［9］。李正良等提出了復雜山地風場平均及脈動風速均方根計算修正模型［10］。文獻［11?15］較系統地研究并分析了峽谷長度、山頂間距、山脈坡度3 種地貌因素對平均風加速效應的影響。目前對于山地線路風偏的研究大多只考慮了橫向風速，并未考慮豎向風速的影響。因此考慮豎向風速，準確計算線路的風偏響應，對于架設在山脈中輸電線路防風偏設計具有重要的借鑒和指導意義。

影響輸電線路豎向風速的主要因素包括：線路架設位置、桿塔呼稱高、山脈坡度。因此本文建立了不同山脈坡度的山地風場，得到線路各點的平均橫向風速和豎向風速隨線路架設位置、桿塔呼稱高、山脈坡度的變化規律。計算了線路在山地風和平地風下的風偏響應，通過風偏角增大百分比來量化三種因素對線路風偏的影響。最后，用響應面方法得到位置、呼稱高、坡度三種因素和風偏角增大百分比的二次回歸方程，分析了三種因素對風偏角的影響規律。

1 山脈風場的數值模擬

1.1 山脈地形模型

本文山體橫斷面選用余弦型山體。山脈三維模型及線路位置如圖1所示。其中：H表示山體高度（本文中山體高度統一取100 m），L表示山脈長度（統一取600 m），D表示山脈底部直徑，則山脈的坡度可表示為2H/D。線路沿山脊布置為縱向跨越山脈，垂直山脊方向為橫向，風向為橫向吹向山脈。

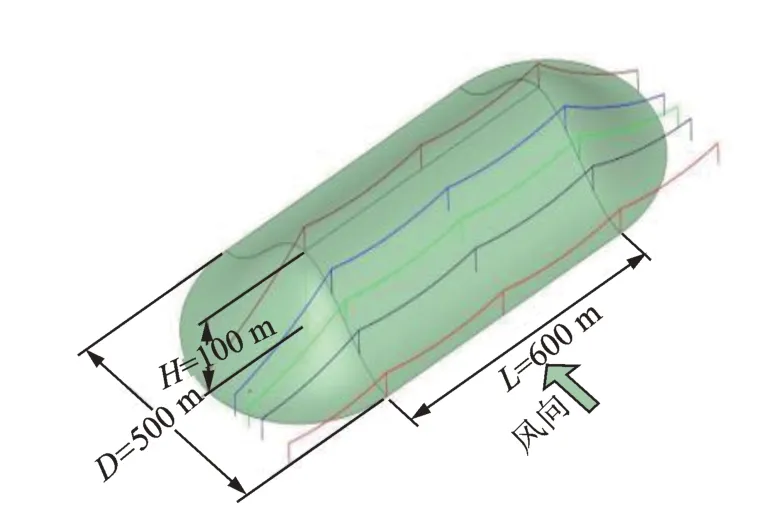
圖1 山脈模型及線路位置Fig.1 Mountain model and transmission line location

1.2 CFD 數值模擬

1.2.1 計算域及網格劃分

利用ANSYS 軟件中的SPACECLAIM 建立山脈模型，并用ICEM 劃分網格。其中計算域高度為6倍模型高度，計算域長度：山前取3 倍模型長度，山后取9倍模型長度，寬度為3倍模型迎風寬度［16?17］。計算域采用結構化六面體網格，山體表面最大網格尺寸為10 m，增長率為1.1，豎向網格首層高度取為1 m，增長率為1.05。計算域模型及網格劃分如圖2所示。

圖2 計算域模型及網格劃分Fig.2 Computational domain model and meshing

1.2.2 入口邊界條件

入口邊界條件的設定對于模擬的結果準確與否有顯著的影響，入口剖面包括平均風剖面和湍流風剖面，參照GB 50009—2012 建筑結構荷載規范［18］中使用的指數率模型，平均風剖面的計算公式為：

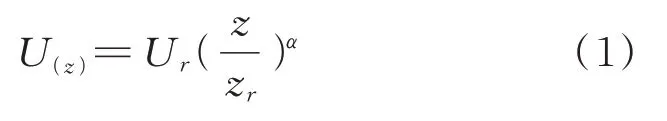
式中U(z)為離地高度z處的平均風速，Ur為參考高度zr處的平均風速，α為地面粗糙度指數。

湍流風剖面計算包括湍動能和耗散率兩個參數，為實現入口剖面的自保持性，對湍流動能k（z）和耗散率?分別采用下公式來計算：

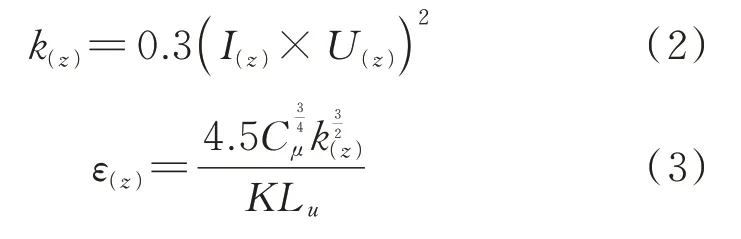
式中K=0.42，Cμ=0.09，I(z)為z高度處湍流度，Lu為湍流積分尺度。

這兩個參數均采用日本規范［19］中的公式：（zg為梯度風高度，B 類地貌下zb=5 m）：

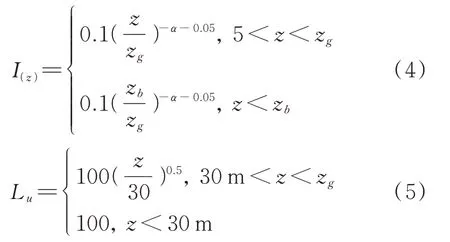
1.2.3 其余參數

湍流模型采用Realizablek?ε湍流模型，選用非平衡壁面函數，計算域入口為速度入口，出口為自由出口，兩側和頂部為對稱邊界，平地和山體表面為固定壁面。根據Franke 等［20］的研究，fluent 軟件中粗糙度高度（roughness height）ks與空氣動力學中粗糙度長度Z0的換算關系為ks=20Z0，B 類風場中對地貌粗糙度Z0的規定地表為0.025，山體表面為0.05，這里取山體和平地的粗糙高度分別為1 和0.5 m。

為驗證入口邊界條件合理性，本文建立一個H=100 m，D=200 m，L=300 m 的孤立山脈模型，利用上述所示的計算域和入口邊界條件計算公式進行計算。并隨機選取山體前一點處繪制風速剖面圖，如圖3所示。從圖中可以看出，山前風剖面和入口風剖面兩點的風剖面幾乎一致，說明邊界條件設置合理。

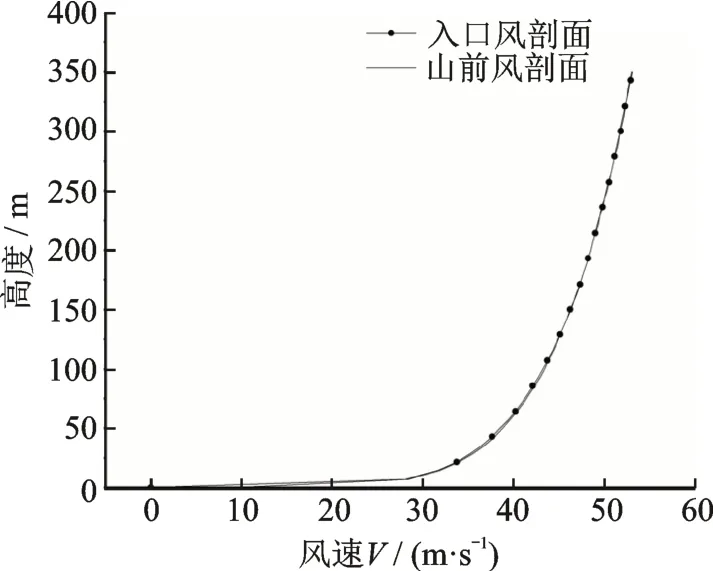
圖3 自保持性驗證（山前及入口處風剖面）Fig.3 Self?preservation verification（wind profile at the pied?mont and inlet）

2 輸電線路參數和計算工況

2.1 輸電線路參數

線路走向如圖1中所示，采用“耐張塔?直線塔?直線塔?直線塔?耐張塔”組成4 檔輸電線路，跨內無轉角。線路電壓等級為500 kV，B 類地區，基本風速V0=30 m/s，導線型號4×LGJ?400/35，絕緣子型號XWP2?160。為便于比較不同地形導線各點風速，每檔導線均劃分45 個單元，整條線路節點個數為181。

2.2 導線風荷載及風偏響應模擬

在有限元軟件中模擬導線風偏時，將四分裂導線等效為一根導線，并將截面積、風荷載等參數做等效化處理。將導線離散成多段索單元，計算每個單元所承受的風荷載，作為靜力施加到節點上。每個單元所受風荷載計算公式：

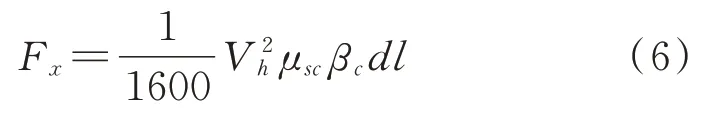
式中Fx為單元所受風荷載，Vh為單元所在高度h處的風速，μsc為導線體型系數，取1.1，βc為風荷載系數，計算風偏時取1，d為導線直徑，l為單元長度。

2.3 計算工況

為定量分析由于山體的存在會對絕緣子串風偏角產生的影響，本文設置兩種計算工況：

工況一：風速Vh取值按照《110kV?750kV 架空輸電線路設計規范》［21］中平地地形計算方法。即

工況二：風速Vh按方向分別取山脈中橫向風速Vx和豎向風速Vy，同時作用在導線上。

基于不同工況下直線塔絕緣子串風偏角，定義風偏角增大百分比為：

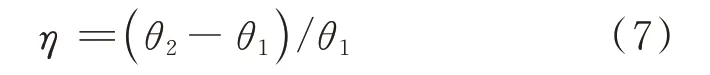
式中θ1，θ2，分別為工況1，2 的山脈中間直線塔絕緣子風偏角計算結果。

3 山脈不同位置輸電線路風偏特性

3.1 模型工況

山脈迎風面上不同位置的風場特性不同，因此輸電線路所承受的橫向風速和豎向風速也有所變化。本節通過改變線路架設高度來改變線路在山脈中的位置。所有涉及到的數值模擬地形工況如表1所示。

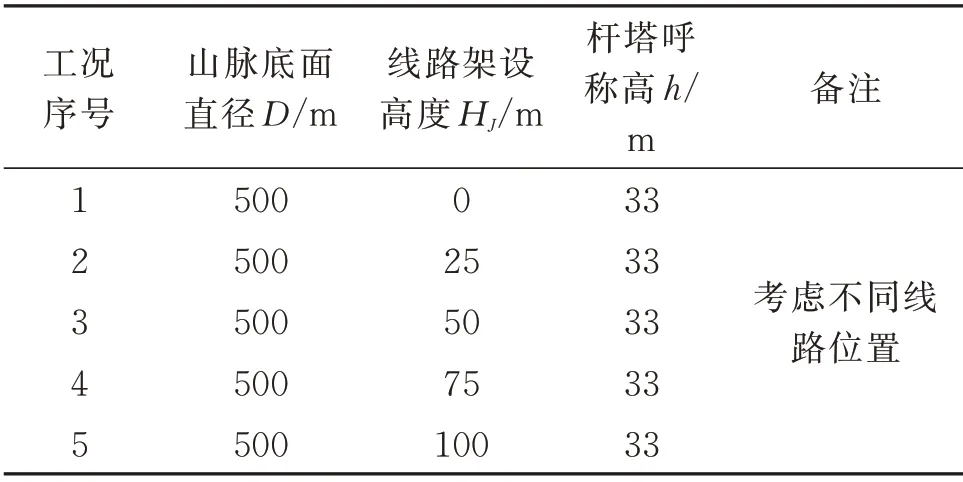
表1 線路及山脈模型參數Tab.1 Transmission lines and mountains model parameters

3.2 線路架設位置對風速的影響

根據數值模擬結果可以得到山脈中各個位置線路上的風速（山地風），為了研究由于山體的存在會對線路上風速產生怎樣的影響，將各個位置的線路放在常規大氣邊界層中，即可得到線路的平地風。迎風面上不同位置處輸電線路所受山地橫向風速，及平地風速如圖4所示。由圖可知，相比于同等高度下的平地風，線路所受橫向風速顯著減小，并且隨著架設高度的增加，風速逐漸增大。只有架設在山脊上的線路風速超過了平地風速。山坡上的風速小于平地風主要是由于山體的遮擋導致，并且有一部分能量分散到了豎向風。因此山坡迎面風會抑制線路的風偏響應，有利線路安全運行。山脊處形成了明顯的越山風，對風的加速效應顯著，不利于線路安全運行。山坡上各個位置風速變化較大，對于實際山地中輸電線路設計，應考慮具體的架設位置來確定設計風速。

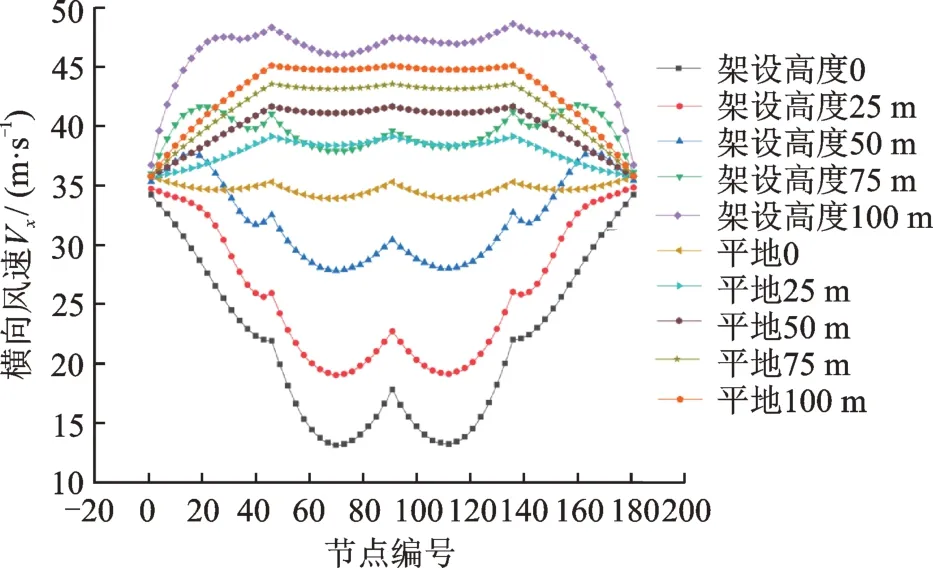
圖4 不同位置橫向風速Fig.4 Cross wind speeds of different positions

不同位置輸電線路所受山地豎向風速和平地豎向風速如圖5所示。由圖可知，平地中線路并不考慮豎向風速，而山坡上豎向風速隨著架設高度的增加先變大后減小，在75 m 高度處達到最大，最大風速甚至達到了來流風速的50%。這是由于地形的影響，導致來流風在爬坡的過程中，豎向風速越來越大，此時，豎向風對于線路風偏的影響不容忽略。因此，對于山坡上的輸電線路設計，應考慮橫向風和豎向風共同作用的影響。

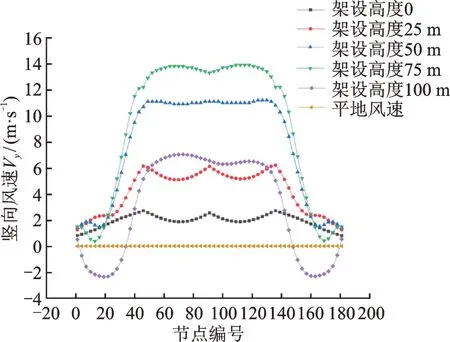
圖5 不同位置豎向風速Fig.5 Vertical wind speeds of different positions

3.3 線路架設位置對風偏的影響

由上節可知，橫向風和豎向風都會對線路風偏產生影響，因此本節通過2.3 節中的方法來求出不同位置處線路的風偏角增大百分比。如圖6所示，隨著架設高度的增加，山體對于線路風偏的影響會越來越不利。在架設高度75 m 以下時，風偏角增大百分比為負，說明位于迎風面山坡，高度在山脈總高度3/4 以下的線路風偏會小于同等高度下的平地線路風偏。對于此處的輸電線路抗風偏設計時可以適當減小設計風速，以節約材料，提高經濟性。而在總高度3/4 以上的線路，特別是在山脊處，要注意越山風對于線路的影響，適當增大設計風速，提高安全性。

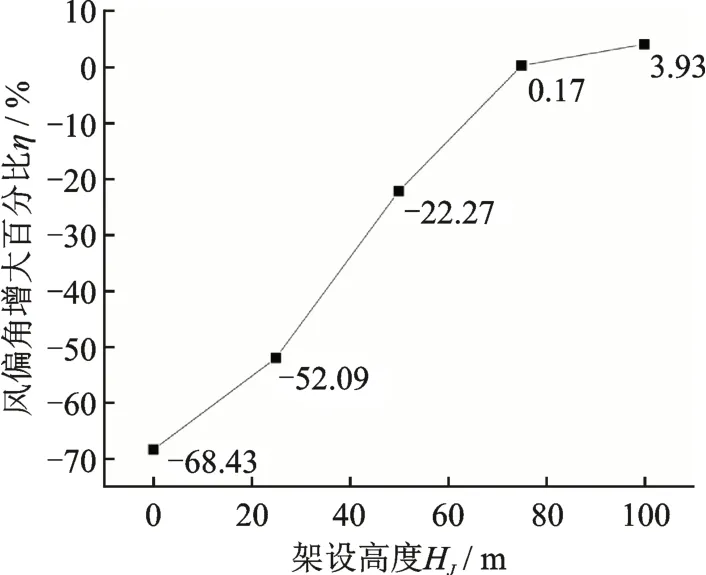
圖6 不同位置的風偏角增大百分比ηFig.6 The percentage increase of the wind?induced swing angle η of different positions

4 山脈中桿塔不同呼稱高輸電線路風偏特性

4.1 模型工況

山脈中對于同一位置的輸電線路，桿塔呼稱高不同也會影響線路所受橫向風速和豎向風速。由上文可知線路架設在75 m 高度處豎向風速最大，豎向風速影響最顯著。如圖7所示，為架設在75 m 高度處線路中間直線塔所在位置，豎向風速的風剖面，其中縱坐標為距離平地高度。山坡上方一定高度內都會產生豎向風速，并且隨著高度的增大，豎向風速逐漸減小。對于輸電線路，呼稱高一般在20～60 m 范圍內，對應圖中95～135 m，此處正是豎向風速最大的范圍。所以，豎向風速對于線路風偏的影響不宜忽略。本章研究桿塔呼稱高變化時，線路上橫向風速和豎向風速及風偏的變化規律。所有涉及到的數值模擬地形工況如表2所示。

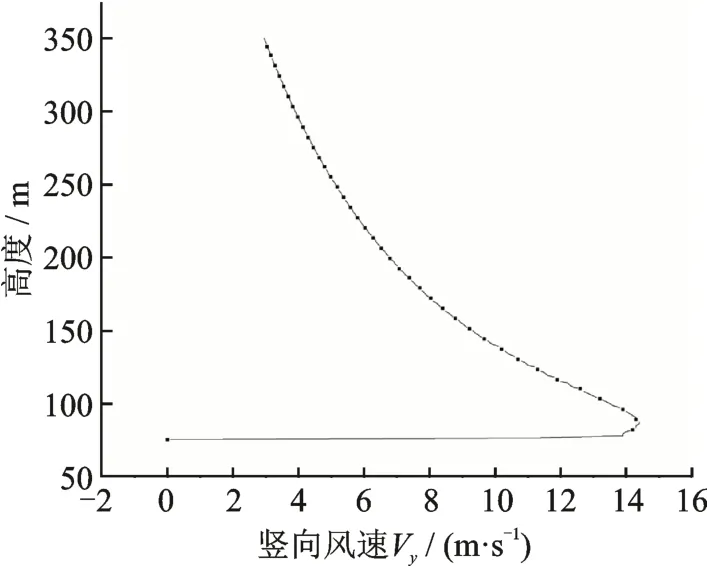
圖7 豎向風速風剖面Fig.7 Vertical wind speed wind profile

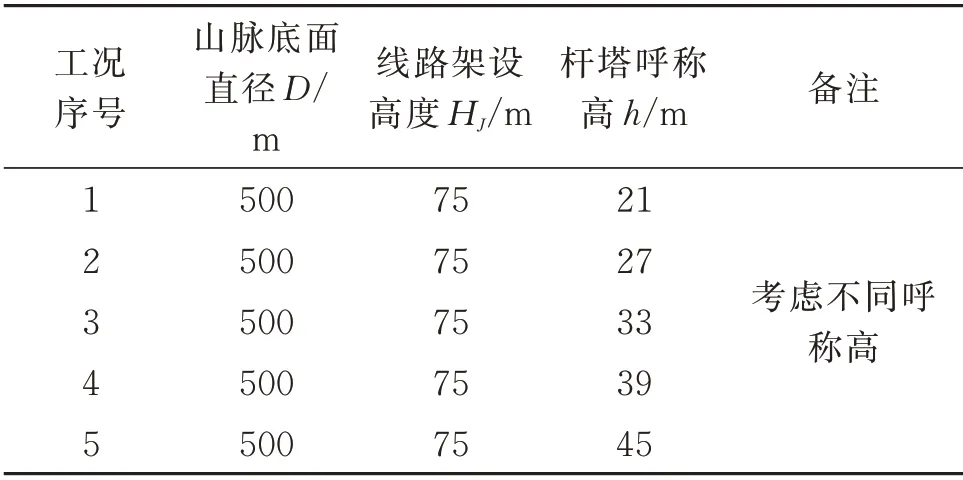
表2 線路及山脈模型參數Tab.2 Transmission lines and mountain model parameters

4.2 桿塔呼稱高對風速的影響

不同呼稱高輸電線路所受山地橫向風速和平地風速如圖8所示。由圖可知，山坡上輸電線路橫向風速隨著高度的增加而增大。而且不論呼稱高多少，山地風速都小于同等高度下平地風速。主要原因同樣是由于山體的遮擋。但是隨著高度的增加，山地風和平地風之間的差距逐漸減小，說明高度越高，山體的遮擋作用越小。

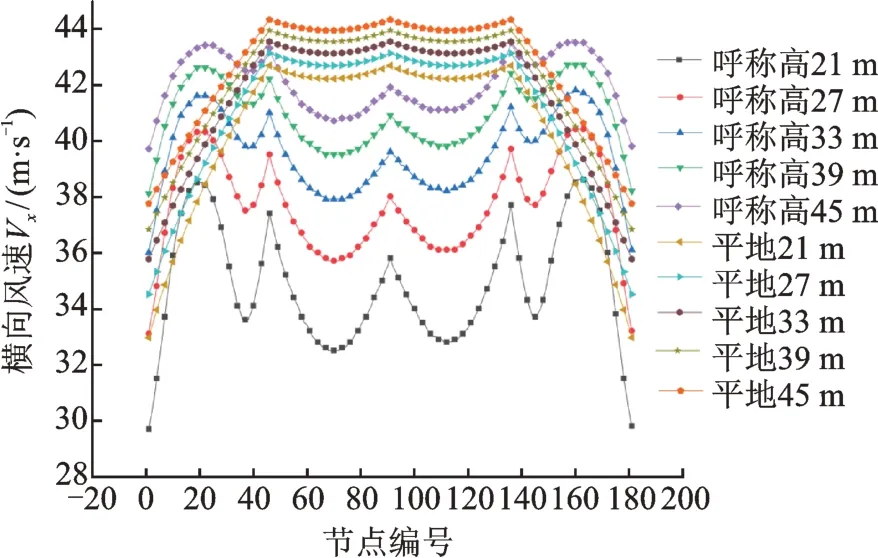
圖8 不同呼稱高橫向風速Fig.8 Cross wind speeds of different nominal height

不同位置輸電線路所受山地豎向風速及平地豎向風速如圖9所示。由圖可知，線路上豎向風速隨著高度的增加而減小。豎向風速是由氣流爬坡產生的，越靠近地面，豎向風速越大，高度越高，受爬坡效應的影響越小。山體的遮擋效應與爬坡效應相同，都是高度越高，影響越小。

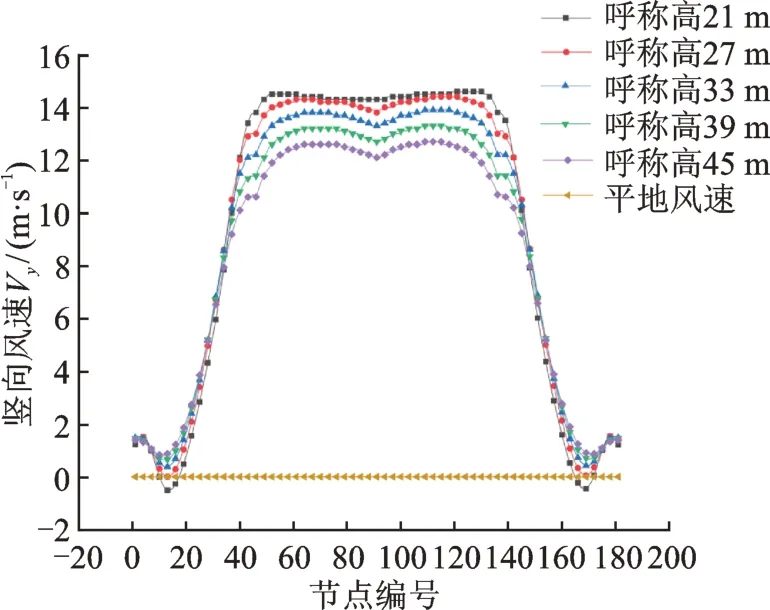
圖9 不同呼稱高豎向風速Fig.9 Vertical wind speeds of different nominal height

4.3 桿塔呼稱高對風偏的影響

同3.3 節計算出不同呼稱高時線路的風偏角增大百分比。如圖10 所示，在呼稱高21 m 時，風偏角增大百分為負，并且較小。結合圖8和9 來看，主要是由于山地橫向風速相對于平地橫向風速過小，雖然有豎向風速的存在，但不足以彌補橫向風速的減小。因此對于山地輸電線路的設計，當呼稱高小于27 m 時，應適當減小設計風速。隨著呼稱高的增加，風偏角增大百分比逐漸增加，并且趨近平穩。主要因為隨著呼稱高的增加，山體的遮擋效應和爬坡效應都逐漸減弱。理論上當高度足夠高時，風偏角增大百分比應趨近于0。但是呼稱高為45 m 時，風偏角增大百分比為1.75。結合圖6來看，在這個高度，豎向風速很大，雖然橫向風速小于平地風速，但由于豎向風速的影響，導致風偏角增大百分比為正。隨著高度繼續增加，豎向風速會迅速減小，橫向風速也會趨近于平地風速，風偏角增大百分比也會趨近于0。

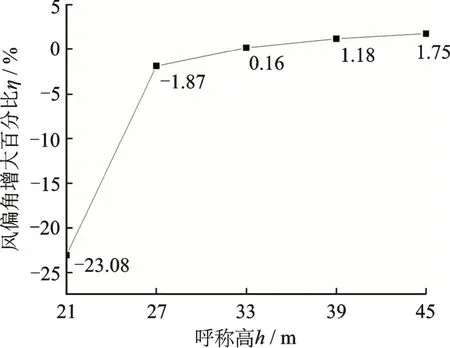
圖10 不同呼稱高的風偏角增大百分比ηFig.10 The percentage increase of the wind?induced swing angle η of different nominal height

5 不同山脈坡度輸電線路風偏特性

5.1 模型工況

山脈坡度不同，山脈中輸電線路的橫向風速和豎向風速也會改變。本節通過改變山脈底面直徑來改變山脈坡度。所有涉及到的數值模擬地形工況如表3所示。

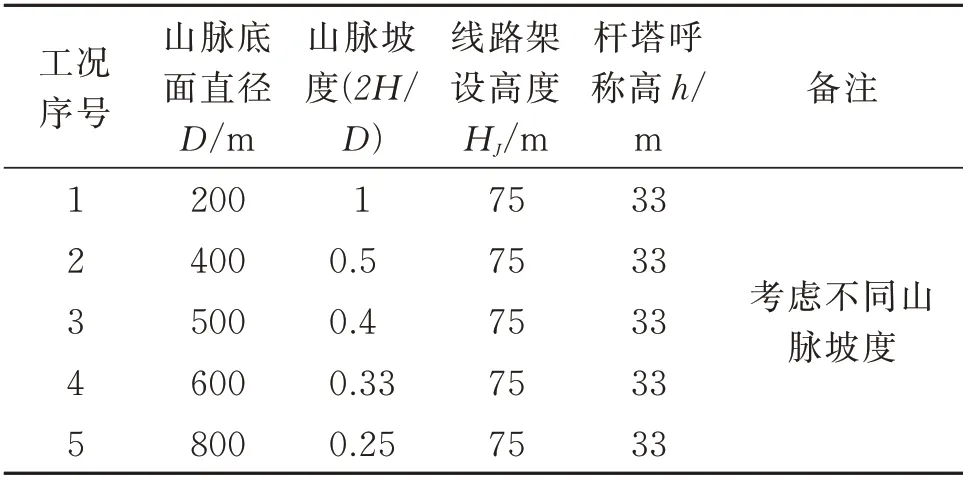
表3 線路及山脈模型參數Tab.3 Transmission lines and mountain model parameters

5.2 山脈坡度對風速的影響

不同山脈坡度輸電線路所受山地橫向風速和平地風速如圖11 所示。由圖可知，隨著山脈坡度的減小，中間兩跨風速逐漸增大，邊跨風速減小。因為坡度越小，山體底面直徑越大，山體蔓延的范圍越大。在來流風吹向山體時，有足夠的距離作為緩沖，可以沿著平緩的山坡順暢地越過山體，不會遇到較大阻擋導致風速驟降。因此山坡對于線路中跨風速的影響主要來源于遮擋效應，坡度越大遮擋效應越明顯，風速越小。對于邊跨，線路所處位置為山體輪廓線處，與山坡有較大不同。此處風速主要取決于地勢，坡度越小，地勢越平緩，加速效應越不明顯，風速越小。

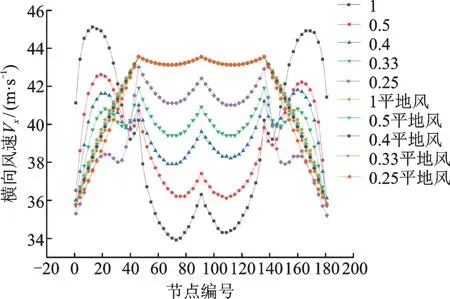
圖11 不同山脈坡度橫向風速Fig.11 Cross wind speeds of different mountain slopes

不同山脈坡度輸電線路所受豎向風速及平地風速如圖12 所示。由圖可知，坡度越大，豎向風速越大。因為陡峭的地形會產生更大的上升氣流，更多來流風能量分散到了豎向風速，導致橫向風速變小，豎向風速變大。尤其在坡度為1 時，豎向風速達到了來流風的2/3。

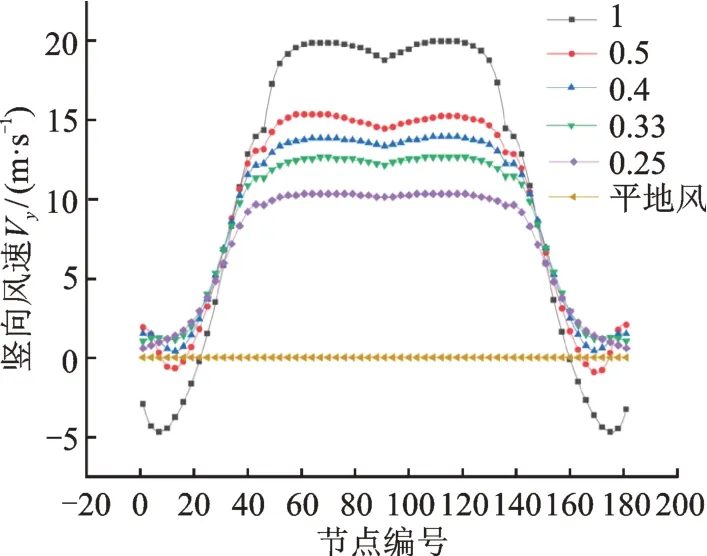
圖12 不同山脈坡度豎向風速Fig.12 Vertical wind speeds of different mountain slopes

5.3 山脈坡度對風偏的影響

同3.3節計算出不同山脈坡度時線路的風偏角增大百分比。如圖13所示，坡度為1時，雖然橫向風速相比平地小，但是豎向風速增大了20 m/s，最終導致風偏角大于平地風偏角。因此在坡度較大時，對于豎向風速的考慮至關重要。坡度為0.5時，風偏角增大百分比突降為負數，從圖12 來看，主要因為豎向風速減小過大，導致豎向荷載不能彌補橫向荷載的減小。坡度在0.5 以下時，風偏角增大百分比逐漸增大并趨于平穩。因為隨著坡度減小，豎向風速越來越小，對線路風偏影響越來越小，橫向風速起到了主要作用。但是隨著坡度不斷減小，橫向風速不會一直增大，只能趨近于平地風速，因此風偏角增大百分比會趨于平穩。

圖13 不同山脈坡度的風偏角增大百分比ηFig.13 The percentage increase of the wind?induced swing angle η of different mountain slopes

6 響應面分析模型

6.1 響應面回歸方程的建立

由于現實中山地地形、線路架設位置、桿塔呼稱高復雜多變，無法通過數值模擬計算出每個地形的η。因此本文采用Box?Behnken 方法進行仿真工況設計，以風偏角增大百分比為響應值（Y），選用線路架設高度（A），桿塔呼稱高（B），山脈坡度（C）為影響因素。

6.2 仿真分析因素及水平及仿真結果分析

本文研究的線路架設高度為0～100 m，桿塔呼稱高為21～45 m，山脈坡度通過底面直徑體現，底面直徑為200～800 m，此范圍為三種因素的水平上下限。仿真分析因素及水平如表4所示，響應面分析響應值結果如表5所示。

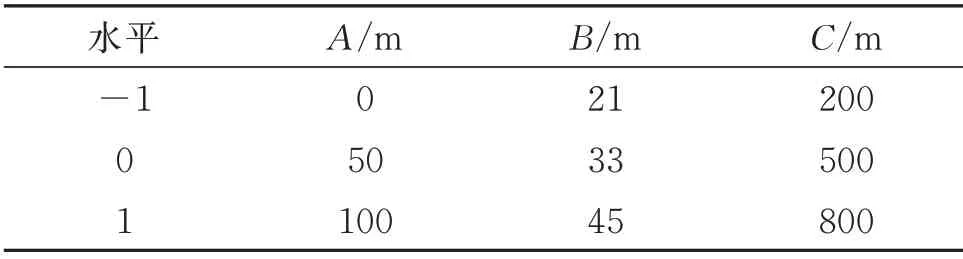
表4 仿真分析因素及水平Tab.4 Simulation analysis factors and levels

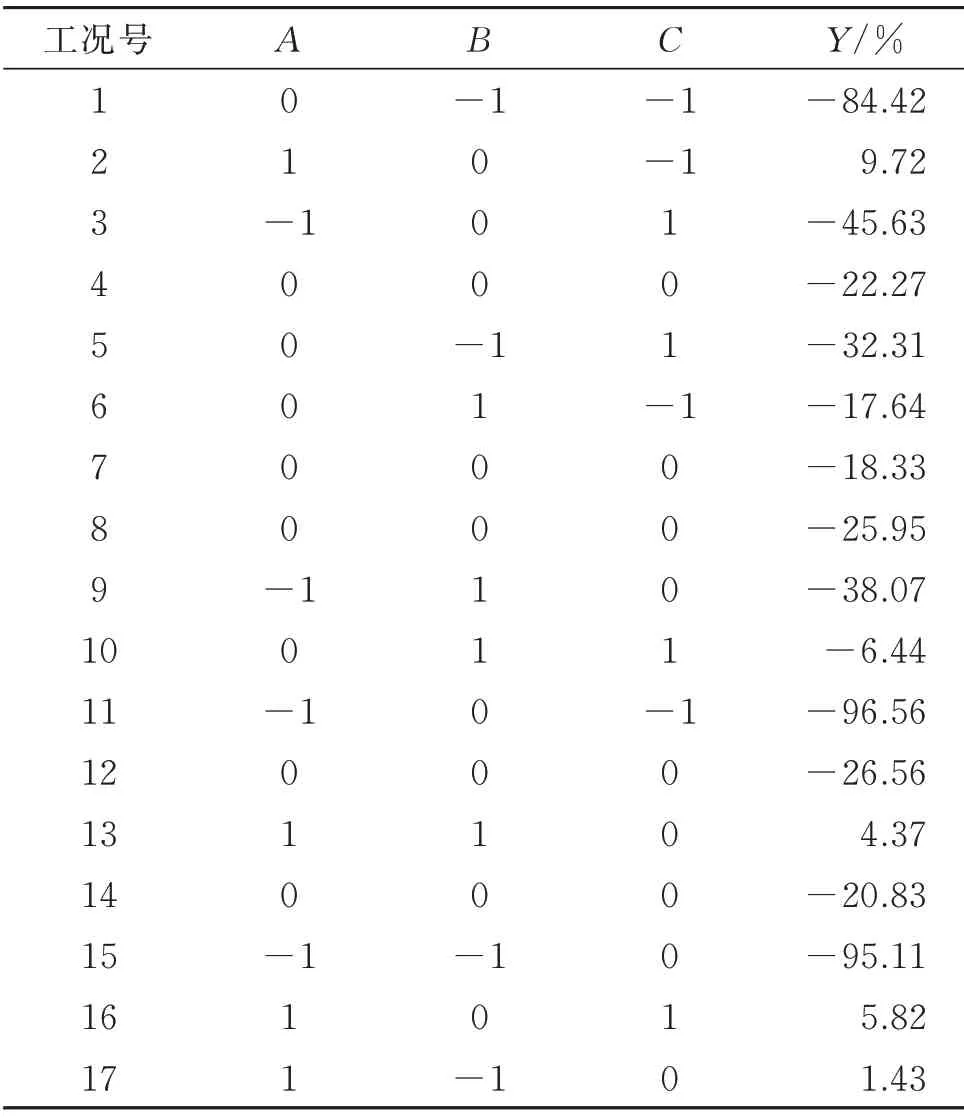
表5 響應值結果Tab.5 Response value result

運用Design?Expert 軟件進行多項擬合回歸分析，得到二次響應面回歸方程為：

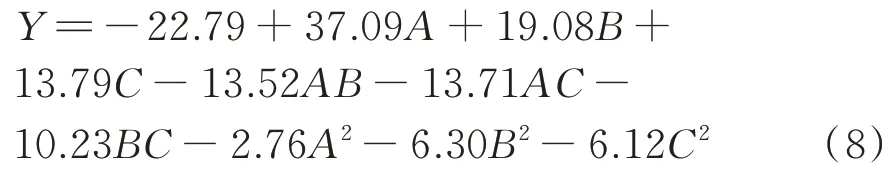
響應面回歸模型方差分析結果如表6所示。

由表6可知，所建立模型的概率P<0.0001，極顯著；失擬項用來表示所用模型與仿真擬合的程度，P=0.0609>0.05，無失擬因素存在；決定系數和R2均大于0.8，說明模型擬合優度較好，因此可用該回歸方程代替仿真真實點對仿真結果進行分析。調整決定系數R2adj=0.9671，表明風偏角增大系數的變化有96.71%來源于山脈坡度、線路架設高度、桿塔呼稱高。經方差分析，其自變量一次項A，B極顯著（P<0.0001）；C，AB，AC高度顯著（P<0.01）；BC顯著（P<0.05）。

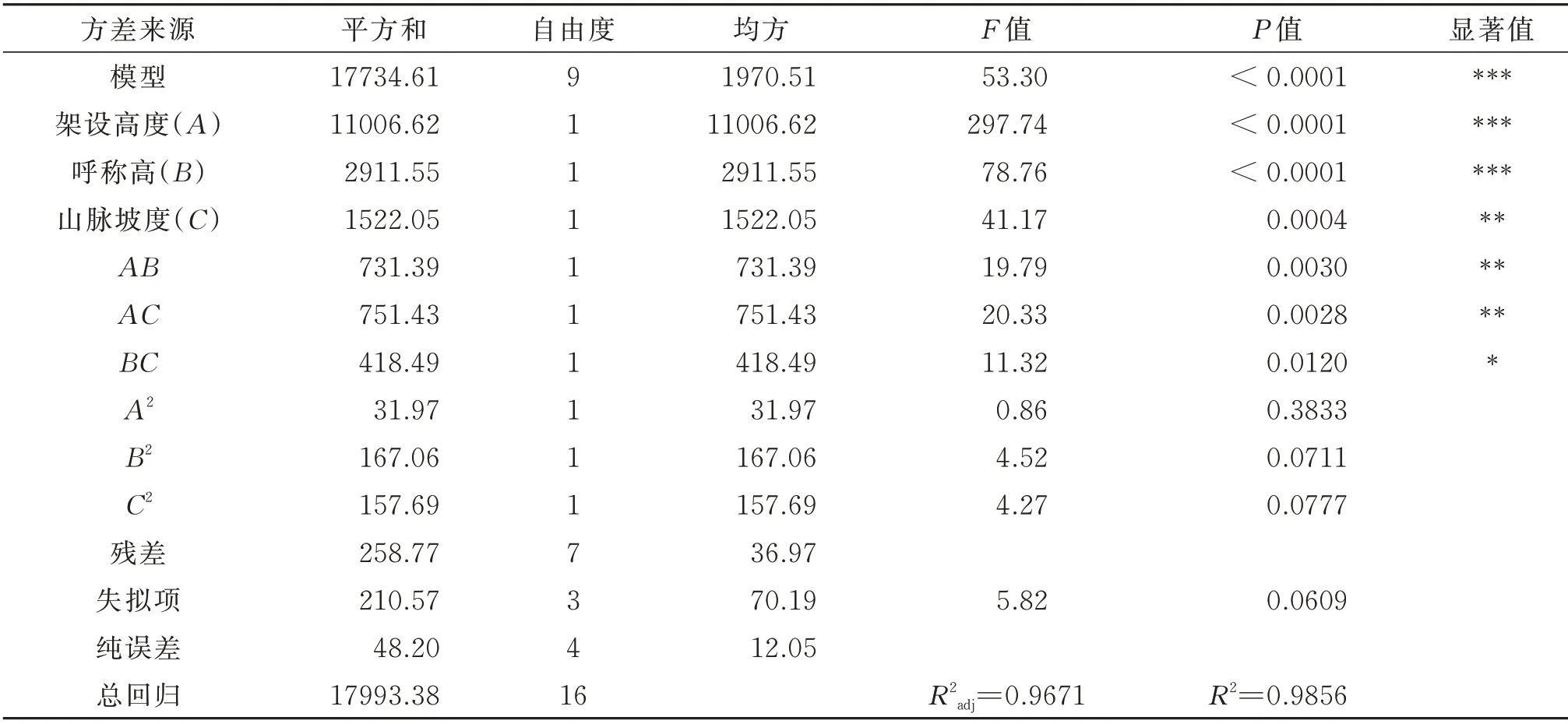
表6 回歸模擬的方差分析Tab.6 Variance analysis of regression model

6.3 各因素交叉相互作用分析

圖14～16 直觀顯示了各個因素交互作用的響應值，圖中各因素的邊線越平坦則該因素對風偏角增大百分比η的影響越小，邊線越陡則該因素對風偏角增大百分比的影響越大［22］。圖中顯示，各因素的陡峭程度為A>B>C，與方差分析結果一致。山脈中線路架設位置對于線路風偏響應的影響至關重要，線路越靠近山脊，風偏響應越大，不利于線路安全運行。

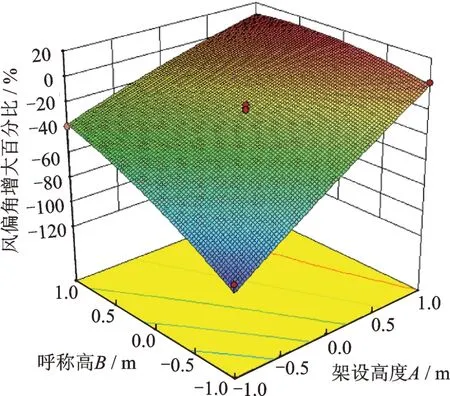
圖14 架設高度和呼稱高對η 影響的響應面Fig.14 Response surface of the effects of erection height and nominal height on the η

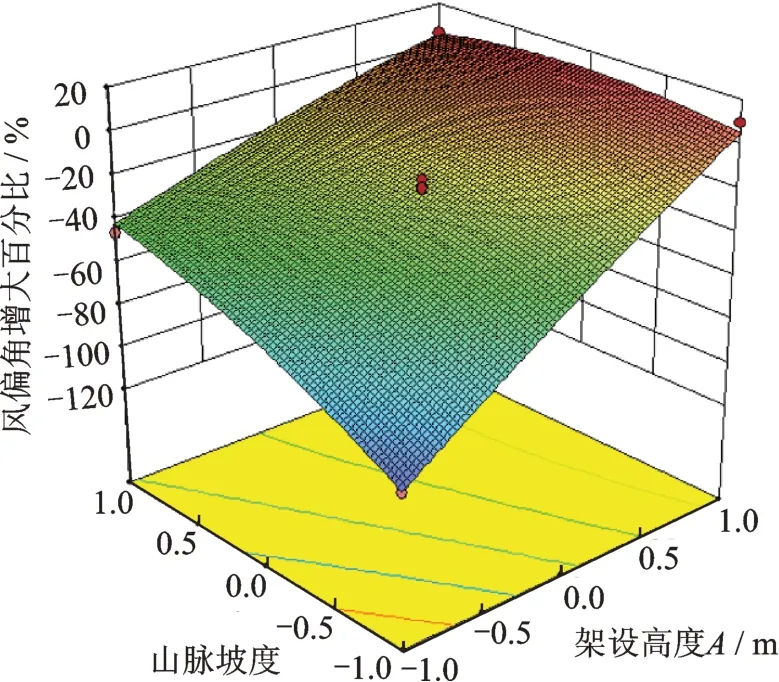
圖15 架設高度和山脈坡度對η 影響的響應面Fig.15 Response surface of the effects of erection height and mountain slope on the η

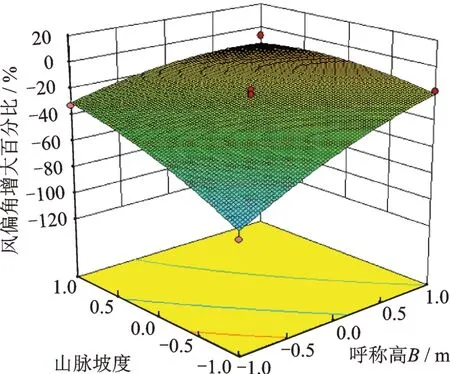
圖16 山脈坡度和呼稱高對η 影響的響應面Fig.16 Response surface of the effects of mountain slope and nominal height on the η

6.4 最大風偏角增大百分比

結合數值模擬和響應面分析結果，可以發現山脈坡度對于風偏角增大百分比的影響規律會根據位置的改變而變化。線路越靠近山脊，呼稱高越高，越不利于線路風偏。由于本文設置了呼稱高上限為45 m，所以根據回歸模型得到最不利于線路風偏的參數為：架設高度為100 m，呼稱高為45 m，山脈坡度為0.79，最大風偏角增大百分比為15.006%。

7 結 論

（1）對于余弦型山體，架設在山脈迎風面不同位置的33 m 呼稱高線路，高度在山脈總高度3/4 時線路豎向風速最大，能達到來流風速的一半。對于高度在山脈總高度3/4 以下的線路，設計時可以適當減小設計風速提高經濟性。而在總高度3/4 以上的線路，應適當增大設計風速，提高安全性。

（2）當線路架設在75 m 高度，山脈坡度為0.4 時，隨著線路呼稱高的增大，橫向風速會變大，豎向風速會減小。當呼稱高小于27 m時，應適當減小設計風速。

（3）對于75 m 高度處33 m 呼高的線路，隨著山脈坡度減小，線路上橫向風速變大，豎向風速減小。風偏角增大百分比先減小后增大，并趨于穩定，在坡度為1 時應適當增大設計風速。

（4）三種因素對風偏角增大百分比影響的靈敏度從大到小依次為架設高度、呼稱高和山脈坡度。其中，線路越靠近山脊，呼稱高越高，越不利于線路風偏。風偏角增大百分比隨坡度的變化規律取決于線路位置。在本文研究的模型范圍內，架設高度100 m，呼稱高為45 m，山脈坡度為0.79 時，風偏角增大百分比達到最大15.006%。