慣性耦合的三自由度導線舞動穩定性和慣性質量防舞機理

溫作鵬，樓文娟，姜 雄，2

（1.浙江大學結構工程研究所，浙江杭州 310058；2.杭蕭鋼構股份有限公司，浙江杭州 310058）

引 言

導線舞動是一種對輸電線路危害較大的失穩振動，準確、清晰地認識舞動激發機理有助于防治舞動。舞動機理的研究最早是從單自由度系統開始的，隨后的研究逐漸轉向二自由度、三自由度系統。早期的Den Hartog 舞動機理［1］解釋了豎向單自由度系統的舞動現象。豎向單自由度系統因其簡單實用，廣泛用于許多舞動研究中［2?3］。三自由度系統的舞動問題則較為復雜，涉及水平、豎向、扭轉三個方向的運動，并且受到系統各向頻率、氣動阻尼、氣動剛度、慣性耦合等多重因素綜合影響。

目前的舞動穩定機理研究往往忽略了氣動剛度或慣性耦合的作用［4?6］，但有研究表明，二者均可能對舞動產生顯著影響。Yan 等［7］對考慮慣性耦合的三自由度系統進行研究，發現慣性耦合顯著改變了系統的舞動穩定性。伍川等［8］采用有限元方法研究導線舞動，結果表明偏心覆冰作用下的導線舞動幅值變大，舞動形態更為復雜。但現有研究均未能解釋慣性耦合對舞動的影響機理。樓文娟等［9?11］的研究則發現，氣動剛度效應能夠解釋試驗中觀測到的舞動風速區間，表明氣動剛度對舞動穩定判斷的重要性。

利用李雅普諾夫一次近似理論，可通過系統特征值實部正負判斷舞動穩定性。對于三自由度系統，其特征值一般難以給出準確的解析解。但在舞動問題中，一般認為結構阻尼、氣動阻尼、慣性耦合對特征頻率影響很小，可以視為小量，從而可采用小參數攝動理論求得近似解析解，即矩陣特征值攝動法［12］。利用該方法，Luongo 等［13］推導了平動二自由度系統特征值的共振解和非共振解，但并未考慮氣動剛度和慣性耦合。姜雄等［14?15］應用矩陣攝動法推導了三自由度系統覆冰輸電導線離散自振頻率下特征值實部一階攝動解，據此分析了舞動機理，但該攝動解并不能反映慣性耦合的影響。

導線防舞裝置都是依據已有的舞動機理設計出來的，但由于舞動問題的復雜性，目前對舞動機理的認識并不清晰，防舞裝置的應用效果不盡如人意。若能獲得更加完備、準確的系統特征值實部解析解，則可對舞動機理有更準確的認識，有助于改進現有防舞器的控制策略，并發展出更加有效的防舞裝置。

慣性型防舞器是導線上廣泛應用的一類防舞裝置，包括雙擺防舞器、偏心重錘、失諧擺、壓重等［16?17］。這類防舞器通過對導線附加慣性質量，改變導線結構特性以抑制舞動。雙擺防舞器通過運動方程的Hurwith 穩定性判據來判斷舞動穩定狀態，但這種數值判據方法缺乏對防舞機理的分析，而實際運行中雙擺防舞器在某些氣象條件下的控制效果并不好。因此，研究附加慣性質量對于結構舞動穩定性的影響機理具有重要意義。

本文針對具有離散自振頻率的三自由度系統，采用修正的矩陣一階攝動解方法推導了同時考慮慣性耦合及氣動剛度的特征值實部修正解。以某D 形覆冰六分裂導線為例，驗證該修正解的準確性。基于該修正解，分析附加質量對舞動穩定性影響的機理，并對輸電線路常用的雙擺防舞器的控制效果及適用性進行檢驗。

1 含附加質量的導線三自由度系統運動方程

取一段含附加質量的導線微元，長度為ds，簡化的三自由度模型如圖1所示。設導線自身的彈性中心與質量中心重合，記為O點，m，J分別為單位長度導線質量、轉動慣量；設共有np個附加質量，mpi，Jpi分別為第i個附加質量的單位長度質量及其轉動慣量，Rpi，αpi分別為附加質量中心與中心O的連線距離、連線的偏心角；R為截面等效半徑，水平來流風速大小為U；ky，kz，kθ分別為單位長度豎向、水平向和扭轉向剛度；記位移向量為U=[v，w，θ]T，v，w，θ分別為豎向、水平向、扭轉向位移。

圖1 含附加質量的導線三自由度模型Fig.1 3-DOF conductor model with additional mass

對非線性風荷載Fw關于結構速度、位移項進行泰勒展開并保留一階項，去除平均風荷載后，運用拉格朗日第二運動方程，并作無量綱和歸一化處理［9］，可求得系統運動方程：

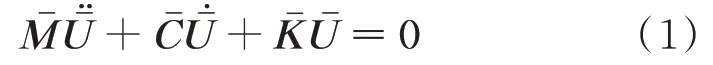
式中s為導線微元沿導線軸向的坐標；sp為附加質量沿導線軸向的坐標；δ為狄拉克函數分別為原系統、附加質量的質量矩陣；分別為結構阻尼、氣動阻尼的矩陣；分別為結構剛度、氣動剛度、附加質量重力剛度的矩陣。

以上為針對導線微元建立的運動方程，對于整檔導線這樣的連續系統，采用假設模態法，令：

式中 假設第j階振型為?j=sin(jπs/L)，n為振型數量，L為導線檔距，qvj，qwj，qθj分別為豎向、水平、扭轉廣義位移。

對式（1）乘以?j并沿導線軸向積分可得：

式中各項的表達式為：

?p為附加質量位置的振型位移；；g為重力加速度；ξy，ξz，ξθ分別為豎向、水平、扭轉向模態阻尼比；N為導線分裂數；ρ為空氣密度；D為導線直徑；CL，CD，CM分別為初始風攻角α0時導線整體的升力、阻力和扭矩系數；C′L，C′D，C′M為前述系數關于風攻角導數。

對于單導線，Ca矩陣第三列相關項表達式為：

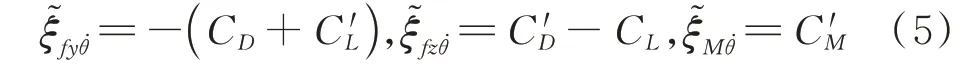
對于分裂數為N的多分裂導線，記sk=sin(α0+αck)，ck=cos(α0+αck)，αck為第k根子導線在多分裂導線截面的方位角。參考郭應龍等［16］給出的表達式，Ca矩陣第三列相關項表達式為：式中CLk，CDk，CMsk分別為第k根子導線的升力、阻力和扭矩系數；C′Lk，C′Dk，C′Msk為前述系數關于風攻角的導數。

2 三自由度系統特征值實部修正攝動解

通過矩陣一階攝動法推得的特征值實部能夠體現氣動阻尼、氣動剛度的貢獻［14］，但無法體現慣性耦合的貢獻。通過矩陣二階攝動法［12］得到的特征值實部理論上能反映慣性耦合的作用，但二階攝動法的計算較為復雜，難以獲得實用的表達式。在文獻［9］的基礎上，本文提出一種修正的攝動解方法，使得一階攝動的特征值實部能反映慣性耦合的作用。

根據特征值攝動理論，當結構參數發生微小變化時，結構參數可描述為零階項（初始值）與一階項（變化值）之和。按照文獻［9］的取法，式（4）中系統質量、剛度、阻尼的矩陣分別表示為：零階項：

一階項：

式中 ε 為小參數。

式（4）的特征方程滿足：

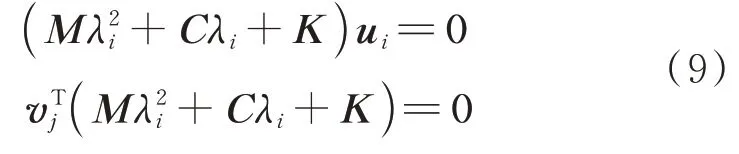
式中λi為第i個特征值，可表示為按ε展開的冪級數：

根據矩陣攝動法，λi的一階攝動解為［9］：

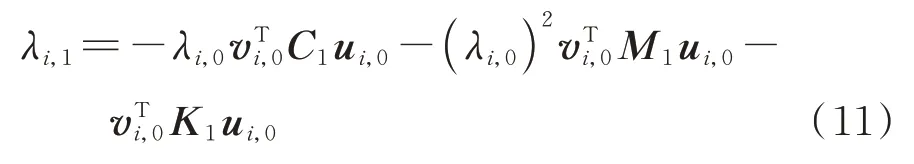
式中vi，0，ui，0為左、右特征向量；記結合豎向零階特征值λ1，0=i 由式（11）可得豎向一階特征值的實部、虛部分別為：

可見附加質量對豎向一階特征值的影響僅體現在其虛部中，而在實部未有體現，即，豎向一階特征值無法反映附加質量對系統穩定性的影響。

下面采用修正的矩陣一階攝動解方法求特征值實部。將εM1視為零階質量矩陣的一部分，得修正的零階質量矩陣為：

在此基礎上，通過小參數展開法求解零階矩陣的特征方程，并忽略高階小量，得修正的零階特征值為：

通過可求得修正的零階左、右特征向量為：

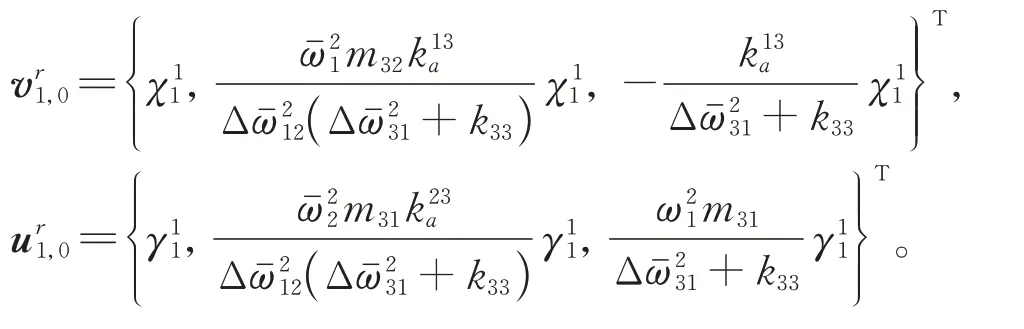
根據特征向量的正交關系，有［15］：

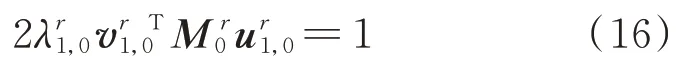
式中 項①對應的-c11/2 項即單自由度系統的特征值實部［9］，項①+②對應原攝動解的表達式（12）［9］；修正攝動解Re()是在原攝動解Re(λ1)的基礎上，新增了慣性耦合相關的附加項③和④，并且項③和④同時還包含氣動阻尼、氣功剛度，可見慣性耦合作用是與氣動力系數密切相關的；附加平動質量m11p與項①+②相乘，其作用在于縮放了原攝動解的數值。此外，假如視附加質量為一階小量，則項③和④均為二階小量，這也解釋了式（12）的特征值實部解為何只包含氣動阻尼項，而不含附加質量項，因為附加質量項僅出現在被舍去的二階小量中。

同上，可得水平向特征值實部為：

pz的表達式可由py中各角標1 全部置換為2 得到，便不在此給出。

扭轉向特征值實部也可通過上述方法得到，但由于扭轉向與兩個平動方向均存在耦合，推導過程較為復雜，這里采用一種簡便方法。記矩陣A為：

式中 I 為單位矩陣。給出以下3 個條件：1）本文所求特征值等價為矩陣A的特征值［15］；2）矩陣A所有特征值之和等于矩陣的跡tr（A）；3）特征方程的復數根成對出現且互為共軛復數。根據這些條件，扭轉向特征值實部可表示為：

由式（17），（18）和（20）可知，特征值實部中涉及多個慣性耦合相關項，表達式較為復雜，這表明慣性耦合大大增加了舞動穩定問題的復雜性。但是可以注意到，與包含有正弦、余弦項，意味著當附加質量位于原系統水平中心線或豎向中心線上，豎向或水平向的特征值可以得到簡化，這能為舞動穩定性判斷提供相對簡單的依據。

3 修正攝動解的驗證

3.1 算例參數

如圖2所示，以D 形覆冰六分裂導線為例進行算例分析。導線氣動力參數參見文獻［18］，結構參數見表1。需要說明的是，對于多分裂導線，覆冰一般在截面圓周的各子導線上都有分布，且子導線分裂半徑遠大于覆冰厚度，故在非重覆冰情況下慣性耦合效應較為微弱。而慣性型防舞器的質量一般集中在導線圓截面上某一側，慣性耦合效應較強。因此可以認為覆冰的慣性耦合效應相比于防舞器可以忽略。另外，假設導線為單一模態振動，附加質量設在導線跨中，則?p=1。定義附加質量的質量比為：

表1 D 形覆冰六分裂導線參數Tab.1 Parameters of the 6-bundled conductor with D-shaped icing

圖2 D 形覆冰六分裂導線Fig.2 6-bundled conductor with D-shaped icing

在單自由度系統的假設下，式（6）的對應扭轉向氣動阻尼。易知若各子導線的氣動力?風攻角曲線相同，中正余弦相關項為零，此時滿足3CD+C′L的形式。與Den Hartog 系數CD+C′L比較易知，3CD+C′L<0的風攻角范圍顯著小于CD+C′L<0的風攻角范圍。一般情況下各子導線氣動力曲線之間差異不會很大，因此可認為多分裂導線的豎向激發舞動占主導情況，扭轉向激發舞動較少發生。由圖3可知，對于該D 形覆冰六分裂導線，CD+C′L<0 的范圍主要為67°～79°，138°～180°，而在全風攻角范圍內大于0。因此對于該多分裂導線，只需重點關注其豎向激發的舞動。

圖3 氣動力相關參數曲線Fig.3 Aerodynamic coefficients

3.2 驗 證

下面以單個附加質量為例，默認取質量比為0.1，偏心角為30o，特征值實部修正攝動解與數值解的比較如圖4（a）所示。由圖可知，三個方向的修正攝動解總體上與數值解吻合良好，在高風速下開始逐漸偏離。圖4（b）對豎向特征值實部的數值解、單自由度解、原攝動解Re(λ1)、修正攝動解Re()進行比較。其中單自由度解指的單自由度系統運動方程的特征值實部［9］，與傳統的Den Hartog 舞動機理是一致的。如圖4（b）所示，單自由度解在8 m/s 風速左右開始顯著偏離數值解，攝動解在13 m/s 左右顯著偏離數值解，而修正攝動解在20 m/s 以內都吻合良好。需要說明的是，在不同氣動力條件下，各近似解與數值解的誤差情況均不相同。由式（17）可知，誤差取決于表達式中附加項的大小。這些附加項在推導過程中被視為小量，但若高風速下氣動負剛度過于顯著而使分母接近零，則誤差會明顯增大。

圖4 特征值近似解與數值解的比較（風攻角76o）Fig.4 Approximate solutions and numerical solution of eigen value real parts（76°attack angle）

圖5給出了0°～180°風攻角下豎向特征值實部數值解、原攝動解Re(λ1)、修正攝動解Re()的比較。如圖5所示，在大部分風攻角區域，修正攝動解的精度均顯著高于攝動解。而在某些風攻角下，兩種攝動解與數值解均較為接近，這表明慣性耦合的影響在該風速下并不顯著。由于慣性耦合項與氣動剛度、氣動阻尼參數是密切相關的，因此慣性耦合能發揮多大的作用與具體的氣動力參數相關。

圖5 豎向特征值實部隨風攻角的變化（風速20 m/s）Fig.5 Variation of vertical eigenvalue real part with attack angle（U=20 m/s）

4 附加質量的防舞機理分析

4.1 附加質量對系統穩定性的影響

如式（17）所示，考慮慣性耦合的攝動解表達式很復雜，涉及多個氣動剛度項、氣動阻尼項，因此難以直接利用式（17）對導線舞動穩定性進行分析。但自然界中有一些覆冰是形成于導線的正下方，而一些常用的導線防舞裝置的質心也是位于導線的正下方，如失諧擺、雙擺防舞器等。在這種情況下，式（17）中m31p=0，豎向?扭轉的慣性耦合作用消失，則特征值實部表達式得以大大簡化，為舞動穩定分析提供方便。

取m31p=0，附加質量后與原系統的的特征值實部之差為：

式中i=1，2，…，np。注意上式中m11p相關項已經被忽略，因為在舞動臨界風速附近，與m11p相乘的阻尼項接近0，對臨界風速影響很小。由式（22）可知，附加質量前后，特征值實部改變量主要由兩項組成：含m32p的慣性耦合項、含kg的重力剛度項。將m32p，kg表達式代入式（22），則式（22）可等價表達為：

由式（23）可知，慣性耦合、重力剛度這兩項均存在與氣動力參數的耦合，包括C′L，C′M，CL-C′D等。因此可以推斷附加質量對系統舞動穩定性的影響強烈依賴于具體的氣動力條件。此外，慣性耦合、重力剛度項均與k13a這個氣動剛度項相乘，可以推斷這兩項在高風速下可能會發揮顯著作用。

式（22）和（23）表明，在附加質量引起的慣性耦合與重力剛度作用下，系統的特征值實部可能發生顯著改變，從而引起系統舞動穩定狀態的變化。利用這一特性，可以使用附加質量對導線結構的舞動進行抑制。

4.2 雙擺防舞器控制效果

雙擺防舞器是目前在多分裂導線上應用廣泛的防舞裝置，其通過提高導線的動力穩定性以實現防舞的效果。雙擺防舞器的簡化結構如圖6所示，兩個擺錘質量相等，沿豎向中心線對稱布置。該裝置的設計優化一般針對少數特定的風攻角進行，若選取合適的防舞器參數，則可以有效控制線路舞動。但從工程應用經驗來看，若實際冰風條件超過設計范圍，則線路仍可能發生舞動，這與雙擺防舞器防舞機理不夠明確有一定關系。本文將從特征值實部正負的角度對雙擺防舞器的防舞機理與控制效果進行分析。

圖6 雙擺防舞器簡化示意圖Fig.6 Schematic of double pendulum anti-galloping device

以文中D 形覆冰六分裂導線為例對雙擺防舞器的控制效果進行計算。設定風攻角為76o，防舞器的質量比為0.1，以舞動臨界風速為優化目標對偏心角αp、擺長Rp參數進行優化，優化后偏心角定為30o，擺長為700 mm。相關計算結果見圖7和8 。

如圖7（a）所示，76o風攻角下，附加質量后豎向特征值實部在風速大于10 m/s 的區間顯著下降，臨界風速從8.5 m/s 提升為15.5 m/s。圖7（b）給出式（23）中重力剛度項與慣性耦合項的曲線，可以發現二者均為負數，大小處于同一量級，并且數值在10 m/s 風速以上變得顯著。因此式（23）的重力剛度項與慣性耦合項可以用來解釋附加質量后系統特征值實部顯著下降的現象。

采用Newmark?β 法計算該三自由度導線結構響應時程，如圖7（c）和（d）所示，在13 m/s 風速下，未受控結構在約90 s 時進入穩定舞動狀態，而受控結構并不舞動。可見附加的質量使得系統特征值實部由正變為負，從而使結構從原先的舞動狀態轉變為氣動穩定狀態，有效抑制了舞動。

圖7 在76°風攻角下結構受控前后變化Fig.7 Comparison of controlled and uncontrolled structure at 76°attack angle

附加質量對于舞動的控制效果實際上取決于具體的氣動力參數。保持原76o風攻角下設計的雙擺防舞器參數不變，對167o風攻角下的控制效果進行計算。如圖8（a）所示，原結構的特征值實部曲線始終小于0，而附加質量后，受控結構的特征值實部在高風速區域顯著抬升并且由負變正，臨界風速為10.1 m/s。圖8（b）表明，重力剛度項、慣性耦合項的曲線數值均大于0。因此對于同樣的雙擺防舞器參數，當風攻角從67o變為167o時，式（23）的C′L，C′M，CL-C′D等氣動力參數發生相應改變，重力剛度項、慣性耦合項起到了增大特征值實部的作用，使結構趨向于氣動失穩。

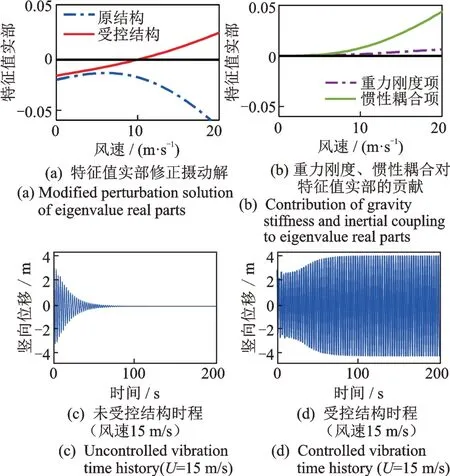
圖8 在167°風攻角下結構受控前后變化Fig.8 Comparison of controlled and uncontrolled structure at 167°oattack angle

由圖8（c）和（d）結構位移時程可知，在15 m/s風速下，未受控結構并未發生舞動，而受控結構發生了大幅度舞動。可見在167o風攻角下，所施加的雙擺防舞器能夠使導線結構從原先的穩定狀態轉變為舞動激發狀態，這與特征值實部計算結果一致。

綜上所述，借助慣性耦合、重力剛度的作用，針對某風攻角優化設計的雙擺防舞器能夠在該條件下有效地抑制舞動。但若風攻角及其氣動力條件發生改變，雙擺防舞器可能失去效果，甚至使原本穩定的結構發生舞動。

5 結 論

本文針對具有離散自振頻率的三自由度系統，采用修正的矩陣一階攝動解方法推導了考慮慣性耦合及氣動剛度的特征值實部修正解。以某D 形覆冰六分裂導線為例，通過與數值解對比以驗證該修正解的準確性。基于該修正解，分析了附加質量對舞動穩定性影響的機理，并對輸電線路常用的雙擺防舞器的控制效果進行計算。結論如下：

1）該修正解相較于原攝動解，附加了水平?豎向、豎向?扭轉這兩種慣性耦合項，且慣性耦合作用與氣動力參數密切相關。與數值解的對比表明，該修正解能夠較準確地反映附加質量對系統穩定性的影響。

2）考慮慣性耦合時系統穩定性判斷式較為復雜，但當附加質量關于導線豎向中心線對稱時，僅需考慮水平?扭轉慣性耦合作用，豎向特征值實部的表達式大為簡化，可用于舞動穩定分析。

3）對修正解的分析表明，附加質量主要通過重力剛度、慣性耦合影響系統的穩定性，這種影響與具體的氣動力參數相關。通過該修正解可以分析導線舞動與慣性質量防舞的機理，為防舞器設計優化提供指導。

4）對雙擺防舞器的計算表明，針對某風攻角優化設計的防舞器能有效抑制舞動；但若風攻角及氣動力條件發生改變，則防舞器可能喪失控制效果，甚至使原本氣動穩定的線路發生舞動。