應變功率譜密度傳遞比與工作應變模態參數識別

王世東，任偉新

（1.合肥工業大學土木與水利工程學院，安徽合肥 230009；2.深圳大學土木與交通工程學院，廣東深圳 518060）

引 言

模態參數是結構固有的動力特性，通過識別模態參數可以對結構的工作狀態進行評估。傳統的結構模態參數識別基于結構的輸入（激勵）和輸出（響應），對于處于運營（工作）狀態下的橋梁、建筑、核反應堆、大壩、海上平臺等大型土木工程結構，要準確測得結構所受到的激勵非常困難，而且做不到實時監測。工作模態參數分析（Operational Modal Anal?ysis，OMA）是僅基于響應數據，即只需測試結構響應信息，完成模態參數識別的過程，此時一般將結構工作期間所受的激勵（環境激勵）假定為白噪聲。基于環境激勵的結構工作模態參數識別方法快速發展，并形成了一系列較為經典的方法，如峰值拾取法（Peak?picking，PP）、頻域分解法（Frequency Domain Decomposition，FDD）、多參考最小二乘復頻域法、NExT 法（Natural Excitation Technique）、特征系統實現算法（Eigensystem Realization Algorithm，ERA）、隨機子空間識別（Stochastic Subspace Identi?fication，SSI）等。大量實踐表明：結構正常工作期間所受激勵難以避免地包含有非白噪聲如諧波成分等，OMA 方法對激勵所做的白噪聲假定與實際激勵有差別，會影響模態參數的識別結果，甚至導致錯誤的識別結果［1?2］。

Yan 等［3］提出了功率譜密度傳遞比（Power Spectrum Density Transmissibility，PSDT）的概念。PSDT 定義為兩響應測點i，j與一參考測點k的互功率譜密度函數Sik和Sjk的比值。從理論上證明了在系統的極點處，PSDT 收斂于兩測點i和j的振型系數之比φi/φj，這一特性與激勵類型和參考點位置的選擇無關。因此，在一種激勵工況下，對相同的測點選擇不同的參考點來計算多組PSDT，在系統極點處，各組PSDT 均相等且收斂于對應測點的振型系數。隨后，張昱等［4］和Li 等［5］細致地論述了以上特性。基于PSDT 的概念，Yan 等［6］進一步提出了改進的PSDT 方法，即PSDT?driven PP 和EPSDT 方法。Araujo 等［7?8］基于PSDT 相繼提出了PSDTM?SVD方法和改進的PSDTM?SVD 方法。結果表明，基于PSDT 的工作模態參數識別方法具有理論價值和實際應用優勢［9］。

經典的模態參數識別指位移模態參數識別，所得到的振型為位移振型［10］。和位移相比，應變對結構的局部損傷（如裂縫、孔洞等）更加敏感，能更好地反映出結構局部特性的變化，在損傷識別領域應用較多［11?12］。早期的模態試驗通過測試位移模態然后借助中心差分法間接得到應變模態［13?14］，為了避免中心差分所產生的數值誤差，學者們研究直接利用應變測試數據來建立應變響應模型。伊立言［15］將應變計用于模態試驗，提出了應變模態的概念。Yam等［16］推導了應變頻響函數（Strain Frequency Re?sponse Functions，SFRFs），給出了應變模態參數（頻率、阻尼、應變振型）識別的實驗測試方法。隨后，許多經典的位移模態分析方法也被引入到應變模態參數識別中，如隨機子空間方法、特征系統實現算法、頻域空間域分解法等［17?20］。

為了實現僅基于應變響應測試的結構應變工作模態參數識別，本文定義了響應應變功率譜密度傳遞比，從理論上證明了其在系統的極點處為應變振型系數之比。利用這一性質，選取一系列不同的參考點構造響應應變功率譜密度傳遞比矩陣，在系統的極點處對該矩陣進行奇異值分解，分解所得左奇異矩陣的第一列向量即為應變振型，從而實現結構工作應變模態參數的識別。該方法不需要對激勵做白噪聲假設，也不需要改變激勵類型，直接通過測試一種工況下的應變響應數據就能識別出結構的應變工作模態參數。

1 應變模態分析理論

由模態分析理論，結構位移響應u由位移振型向量φr和模態坐標qr疊加而成。類似地，結構的應變響應ε也可以用應變振型φεr和模態坐標q′r疊加而成，如下式所示：

位移和應變是結構同一能量狀態的兩種表達，對于第r階模態，應變模態坐標q′r和位移模態坐標qr相等。對于線性時不變系統，模態坐標可以表示為：

式中kr，mr和cr分別代表第r階模態剛度、模態質量和模態阻尼；N表示模態的數目；F表示激勵力的幅值；ω表示圓頻率；j 表示虛數符號，j2=?1；t表示時間。由方程（2）和（3）得到如下式所示的應變模態表達式：

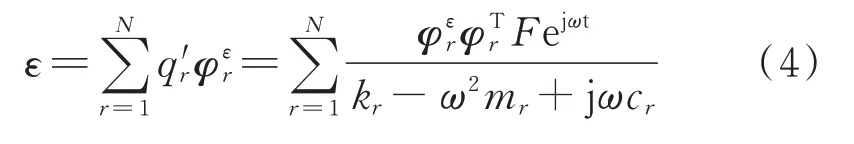
由方程（3）和（4）得到j點激勵，i點響應的應變頻響函數（Strain Frequency Response Function，SFRF）表達式如下：

式（5）表示第r階應變模態振型向量在i測點的系數，φjr由表示第r階位移模態振型向量在i測點的系數，應變頻響函數(ω)組成應變頻響矩陣Hε如下：

將方程（6）寫成如下式所示的極點留數形式：

式中s表示一個復數，表示系統的極點；表示留數矩陣；為第r階模態參與系數向量，其含義是第r階模態在振動響應中所占的比重；和分別為和λr的復共軛，ζr表示第r階模態阻尼比。當不考慮阻尼的影響時有ζr=0，λr=jωr為系統的極點。此時結構的第r階頻率如下式所示：

2 應變功率譜密度傳遞比

對于平穩隨機過程，系統的輸入與輸出有如下關系：

式中S(s)m×m表示響應的功率譜密度矩陣；m為位移響應的測試點數；G(s)n×n表示激勵的功率譜密度矩陣；n表示激勵的作用點數；H(s)為m×n階頻響函數矩陣；H*(s)T表示H(s)的共軛轉置。

由方程（9），點i與點j的互功率譜可以表示為以下方程：

式中表示H(s) 第i行；（s）j表示矩陣H*(s)T的第j列。方程（10）可以寫成如下式所示的累加求和形式：

式中Hik(s)表示i點響應和k點（k=1，2，…，N）激勵之間的傳遞函數；Gkn(s)表示在點k和點n（n=1，2，…，N）上激勵的互功率譜密度；(s)表示j點的位移響應和n點激勵的傳遞函數的復共軛。

選定任一響應測試點p為參考點，i點和j點的功率譜密度傳遞比PSDT 定義為：i點響應yi（t）與參考點p點響應yp（t）之間的互功率譜Sip（s），j點響應yj（t）與參考點p點響應yp（t）之間的互功率譜Sjp（s），兩者之比表示為：

借鑒位移響應功率譜密度傳遞比的概念，定義響應應變功率譜密度傳遞比（Strain Power Spectrum Density Transmissibility，SPSDT），即i點應變響應εi（t）與參考點p點應變響應εp（t）之間的互功率譜，j點應變響應εj（t）與參考點p點響應εp（t）之間應變響應的互功率譜密度兩者之比表示為：

由方程（6）和（9），對于平穩隨機過程，可以建立用應變表示的系統的輸入與輸出關系：

式中Sε(s)m×m表示結構應變響應的功率譜矩陣，m為響應測點；G(s)n×n表示激勵的功率譜密度矩陣，n為激勵作用點數；Hε(s)為m×n階應變傳遞函數矩陣；Hε*(s)T為Hε(s)的共軛轉置。由方程（9），（10），（11）和（14）可得：

則由方程（15）和（13），響應應變功率譜密度傳遞比可以表示為：

式中(s)表示k點激勵，i點響應的應變傳遞函數；Gkn(s)表示在k點和n點的激勵的互功率譜密度。在方程（16）中，取分母與分子有相同下標的項得到εtkn(s)：

當s→λr，εtkn(s)的極限：

式中和分別代表i測點和j測點在第r階應變模態振型中對應的振型系數。在復平面中，當fn（s）和gn（s）（n=1，2，…，N）滿足下式時：

方程（19）中η表示同一常數，可得：

結合方程（16），（18），（19）和（20）可以得到：

同理，當參考點選擇為q點時，可以得到下式：

至此證明了在系統的極點處，SPSDT 等于測點i和測點j的應變振型系數和的比值，這一特性與參考點的選擇無關，只與測點i和j的位置有關。

3 基于SPSDT 的應變模態參數識別

對測點i和j，選擇不同參考點p和q，對SPSDT做差，由方程（21）和（22）可以得到：

當s→λr時：

對方程（24）取倒數記為Δ-1[(s)］，顯然系統的極點是Δ-1[(s)]的極點。需要注意的是，由方程（25）所得到的極點中可能包含與系統極點無關的虛假極點。為了減少虛假極點的出現，融合所有參考點的信息構造如下方程，確定系統的極點：

選定k（k=1，2，…，N）測點為基準點，然后結合其他N個測點和N個參考點的信息，構成SPSDT矩陣εT(s)如下式所示：

由方程（21），（22）和（27），當s=λr時：

方程（28）中應變功率譜密度傳遞比矩陣εT(λr)的秩為1。在λ r處對εT(λr)矩陣進行奇異值分解：

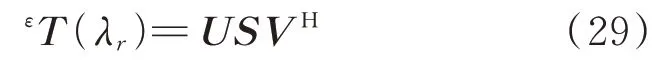
方程（29）中所得到的左奇異矩陣U的第一列向量為第r階應變振型。依次改變k（k=1，2，…，N）的取值，S表示對角線位置的元素由奇異值組成的對角矩陣，VH表示右奇異矩陣。由方程（27），（28）和（29）計算N個向量（k=1，2，…，N）。對以上所得N個向量按照最大值歸一化以后取平均，即可得到應變振型如下式所示：

綜上，基于響應應變功率譜密度傳遞比的結構應變工作模態參數識別過程如圖1所示。

圖1 基于SPSDT 的應變模態參數識別流程圖Fig.1 Flow chart of strain modal parameter identification based on SPSDT

4 數值算例

如圖2所示為三跨連續梁模型，連續梁總長為60 m，跨度為20 m+20 m+20 m。截面為矩形，寬0.6 m，高0.2 m。梁的材料特性如下：密度為7900 kg/m3，彈性模量為210 GPa。采用有限元方法，全橋劃分為60 個單元，每個單元的長度為1 m，單元類型為BEAM188，通過自振分析可得到結構固有頻率。

圖2 三跨連續梁模型Fig.2 Model of 3-span continuous beam

用Matlab 生成61 組服從標準正態分布的隨機數，每組數據包含5000 個數，模擬隨機激勵同步加載到各個節點，對梁做動力時程分析，時間步長為0.01 s，計算節點的應變時程數據。采用建立的基于響應應變功率譜密度傳遞比方法，僅基于應變響應識別梁的應變模態參數。按照最大值歸一化，得到應變模態振型如圖3所示，頻率識別結果比較如表1所示。

表1 頻率識別結果Tab.1 Recognition results of frequencies

值得注意的是，應變模態和位移模態是結構同一種狀態的兩種表達。通常位移模態振型φ和應變模態振型φε是不同的，如圖3所示，圖中位移模態振型由有限元計算直接得到，而應變振型為用本文方法識別得到的。

圖3 位移振型和應變振型Fig.3 Displacement mode shapes and strain mode shapes

對于受彎為主的梁而言，應變是位移的二階導數。有限元計算無法直接計算出應變模態振型，一般由位移模態振型差分2 次得到應變模態振型。本文所建立的應變功率譜密度傳遞比方法，基于結構的應變響應，可以直接識別出結構的應變模態振型。

5 實驗驗證

實驗簡支梁模型的梁長為3.05 m，凈跨為3 m。矩形截面高為22.5 mm，寬為125 mm，材料為鋁合金，密度為2.7×103kg/m3，彈性模量為70 GPa。梁等間距分為20 段，共設置19 個應變測點，測點布置如圖4所示。實驗采用的應變片為電阻式應變計，型號為BX120?3AA，由浙江黃巖測試儀器廠生產，電阻值為120 Ω，靈敏系數為2.08。實驗數據采集使用NI 動態數據采集儀，該儀器包括的組件有NI PXIe?1082、PXIe?8840 控制器、PXIe?4330 應變測試模塊、TB4330 接線盒。簡支梁模型、動態數據采集儀、支座模型和應變片分別如圖4～7 所示。

圖4 簡支梁模型Fig.4 Model of simply supported beam

圖5 NI 數據采集儀Fig.5 NI data acquisition instrument

圖6 支座模型Fig.6 Support model

圖7 應變片Fig.7 Strain gauge

本文給出的SPSDT 模態參數識別法不需要對激勵類型做任何假設，僅利用響應數據就能識別模態參數。因此實驗室做試驗時用小錘敲擊作為加載，加載位置和敲擊力大小隨機。采樣時長為150 s，采樣頻率為1000 Hz。測點10 的時長30 s 的應變時程曲線如圖8所示。

圖8 測點10 時長30 s 的應變時程Fig.8 30 seconds strain history of testing point 10

針對模型實驗梁實測應變響應數據，采用本文SPSDT 方法進行了應變模態參數識別，并采用傳統的頻域分解法（FDD）和隨機子空間方法（SSI）識別，同時給出有限元結果和理論解，五種方法所得固有頻率結果比較如表2所示，結果吻合良好。

表2 頻率結果比較Tab.2 Comparison of frequency results

由SPSDT 方法直接識別出的前四階應變模態振型如圖9所示。各振型按照最大值歸一化處理，表明本文建立的基于響應應變功率譜密度傳遞比結構工作應變模態參數識別方法，僅基于應變響應，不僅能方便地識別出結構的模態頻率，還可以識別出結構的工作應變模態振型。圖9對比了解析應變振型和識別應變振型；表3給出了前四階解析應變振型和識別的應變振型的MAC 值，其中對角項的MAC 均大于0.99，非對角項小于0.01。結果表明兩種方法所得到的結果是一致的。

表3 解析應變振型與識別應變振型的MACTab.3 MAC of analysis strain mode shape and identifi?cation strain mode shape

圖9 簡支梁應變振型Fig.9 Strain mode shapes of simply supported beam

為探討數據長度（采樣時長）對識別結果的影響，選取一段時長4 min，采樣頻率1000 Hz 的應變響應數據，將其劃分成時長為1，2，3 和4 min 的四段數據，進行應變模態參數識別。4 種不同時長的應變數據識別出實驗梁的固有頻率比較如表4所示，所得前四階頻率結果相同。

表4 采樣時長與頻率Tab.4 Sampling time and frequency

對于應變模態振型的比較，采用模態置信準則（Modal Assurance Criterion，MAC）：

式（31）中，當MAC 為0 時，表示兩向量完全無關；當MAC 為1 時，表示兩向量完全相關。以采樣時長60 s 的數據識別出的前四階應變模態振型作為基準，和其他三組不同時長數據做比較。分別取2，3，4 min 時長數據所識別出的前四階應變模態振型計算MAC，各組數據所識別結果不同階次的應變模態振型之間的MAC 均小于0.01，相同階次的應變振型MAC 接近于1。在表5中列出不同時長數據所識別的前四階相同階次應變模態振型之間的MAC值，其中第二列數值為采樣時長1 min 的數據所識別的前四階應變模態振型的MAC。

表5 采樣時長與MACTab.5 Sampling time and MAC

6 結 論

（1）選取一個應變響應測點作為參考點，定義了一個響應應變功率譜密度傳遞比（Strain Power Spectrum Density Transmissibility，SPSDT），從理論上證明了SPSDT 在系統的極點處為應變振型系數之比；

（2）選取一系列不同的響應參考點構造響應應變功率譜密度傳遞比矩陣，在系統的極點處對該矩陣進行奇異值分解，分解所得左奇異矩陣的第一列向量即為應變振型，從而實現結構工作（僅基于響應）應變模態參數的識別；

（3）數值模擬算例和實驗室模型試驗驗證了所提出方法的有效性，并分析了采樣時長對識別結果的影響，結果表明該方法具有較好的魯棒性；

（4）與傳統的工作模態分析方法相比，SPSDT方法不需要對激勵做白噪聲假定，不需要多種激勵類型，僅在一種激勵下，即可識別出結構的工作應變模態參數。