改進MBCV法在滾動軸承故障診斷中的應用

吳 超，崔玲麗，張建宇，王 鑫

（北京工業大學材料與制造學部，北京 100124）

引 言

滾動軸承是旋轉機械設備中的關鍵零件，其運行狀態直接影響到整個機械系統的性能。然而，由于機械設備結構復雜，工況多變，滾動軸承容易出現擦傷、裂紋、點蝕、脫落等局部損傷。據有關資料統計，在機械設備中大約有21%的故障是由軸承損傷引起。因此，為了提高滾動軸承的可靠性，保證機械設備安全運行，研究有效的軸承故障診斷方法非常必要［1?4］。

振動分析法由于其測量簡單，蘊含信息豐富，且對滾動軸承早期故障比較敏感，被廣泛應用于滾動軸承狀態監測與故障診斷中［5］。當軸承表面出現損傷時，損傷點在運行過程中與其他元件產生接觸沖擊，該沖擊由于作用時間短，頻域覆蓋面大，必然會激發軸承系統的固有振動頻率從而產生共振，導致振動信號的幅值和頻率出現調制現象［6?7］。同時，在工程實際中，機械系統中往往還含有其他干擾振動以及大量噪聲，且故障振動信號在經過復雜的傳遞路徑后亦會產生一定的能量衰減，導致滾動軸承的故障特征被掩蓋。因此，軸承故障診斷的一個關鍵是實現信號分離，即從采集的振動信號中分離出軸承故障信號。目前，已有多種信號分離技術被成功用于滾動軸承故障診斷中。

Randall 等［8］提出了一種基于倒頻譜編輯的故障滾動軸承振動信號與齒輪振動信號分離方法，該方法通過人工選取齒輪信號對應的倒頻譜譜線進行編輯，能夠有效去除目標離散頻率成分，分離出滾動軸承振動信號。李紅賢等［9］提出了一種迭代廣義解調的變轉速滾動軸承故障診斷方法。該方法消除了變轉速工作模式下齒輪嚙合對軸承信號干擾的問題，成功提取出了軸承故障信息，實現軸承運行狀態的判斷。張文義等［10］利用信號共振稀疏分解和能量算子解調相結合的方法，將信號分解為高、低共振分量，實現齒輪箱軸承故障信號的分離與診斷。

這些方法均能實現軸承故障信號的分離，但是仍存在一定的局限，不容易實現工程上的自動監測與診斷。為了實現工程上軸承的自動監測與診斷，美國學者Jacek Dybala 提出了一種自動的軸承故障診斷方法［11］。Dybala 將圖像分割的經典算法——最大類間方差法引入到軸承故障信號的信號分離中。這種算法能夠快速將信號頻域分為上下兩個類間方差最大的區間，且通過保留軸承故障信號所在的區間實現信號分離。該方法計算速度快，自適應性強，對于頻譜有明顯峰值差異的信號分離效果較好，但對于頻譜復雜的信號效果不佳，且存在經驗性選擇分離次數的問題。研究發現出現這一問題的主要原因是由于MBCV 法求得的分割閾值對軸承故障信號的適應性較差。

針對這一問題，提出一種基于改進MBCV 法的滾動軸承故障診斷方法。該方法的關鍵在于增強分割閾值的細節表達能力，提高分離效果。首先將信號頻譜均分為若干個子區間，分別求出每個子區間的MBCV 閾值，并將這些閾值進行插值擬合，從而得到整個頻域的閾值曲線；調整頻譜分割段數并以分離信號與原信號之間的均方根誤差最小化為目標尋找最優閾值曲線；然后依據最優閾值曲線分離出軸承故障信號，并使用平方包絡譜提取故障特征。試驗和仿真結果表明，該方法能有效剔除強干擾成分，對軸承故障信號的分離結果更加精確，診斷結果準確率更高。

1 MBCV 算法原理

1.1 MBCV 算法原理

最大類間方差法由日本學者N Otsu 提出，用于自動計算圖像閾值，對灰度圖像進行二值化處理［12］。該方法將灰度圖像按照灰度不同分為目標與背景兩部分，通過計算目標與背景之間的類間方差并以類間方差最大時對應的灰度值作為圖像二值化的標準。對于給定圖像，假設總像素數為N=n0+n1+…+nL-1，灰度范圍為［0，L-1］，則：

式中ni為第i個灰度等級的像素數；pi為像素點出現的概率，pi=ni/N，i=0，1，…，L-1，L為灰度等級。

區間［0，L-1］內任意灰度值k，可以將圖像分為目標c0和背景c1兩部分，分別由灰度值在［0，k］和［k+1，L-1］中的像素構成，c0和c1各部分的灰度均值為：

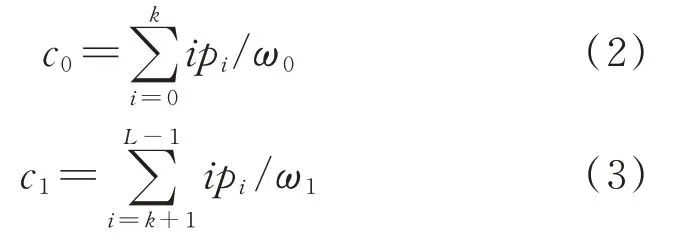
式中ω0和ω1分別為c0和c1兩部分出現的概率，

整個圖像的灰度均值表示為：

下式為c0和c1兩部分的類間方差計算公式：

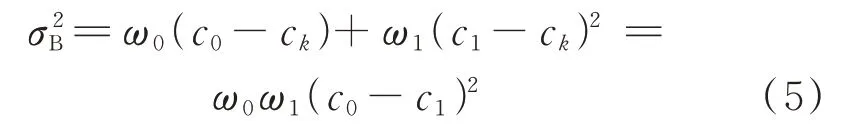
在［0，L-1］區間內，任意一個k值均對應一個類間方差。依據類間方差越大，分類效果越好的原則，確定類間方差最大時對應的k值作為最佳分割閾值。

美國學者Jacek Dybala 將MBCV 方法應用在軸承振動信號的信號分離中。他將圖像各像素的灰度等級對應為信號的頻譜分量的頻率，每個灰度級出現的次數即像素數對應為信號譜分量的振幅，并將公式（5）等效至信號頻譜中，得到頻譜中類間方差計算公式：

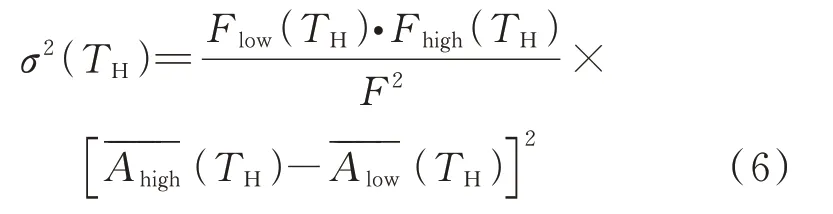
式中F為信號的所有譜頻率分量的數量，Flow(TH) 為低幅值信號頻譜分量的個數，Fhigh(TH)為高幅值信號頻譜分量的個數，(TH)表示低振幅信號頻譜分量的平均振幅(TH)表示高振幅信號頻譜分量的平均振幅。

公式（6）可以自適應地求出信號頻域的最優分割閾值TH。使用該閾值實現信號分離的具體流程如圖1所示。

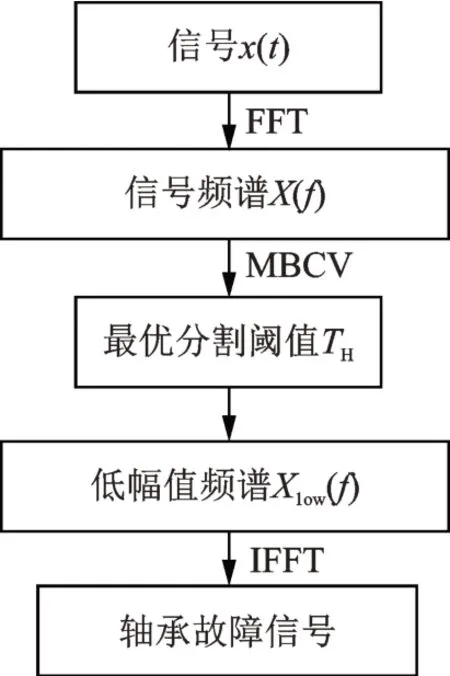
圖1 基于MBCV 法的信號分離流程Fig.1 Signal separation process based on MBCV method

即先根據閾值TH將原信號頻譜分為高幅值區Xhigh(f)，低幅值區Xlow(f)，再通過傅里葉逆變換將Xlow(f)轉為時域信號xlow(t)。

在實際工作環境中，通過振動傳感器采集的信號中含有一些齒輪嚙合和系統共振分量，這些分量的能量相對于軸承故障分量要高。因此，軸承故障信息大都存在于低幅值部分中。所以，這里對低幅值信號頻譜進行逆傅里葉變換得到的信號即為軸承故障信號。

1.2 仿真信號驗證

通過軸承外圈故障仿真信號進一步說明MB?CV 法對振動信號的分類效果。為了模擬軸承的工作環境，在仿真信號中加入兩個正弦信號，該信號如圖2所示。

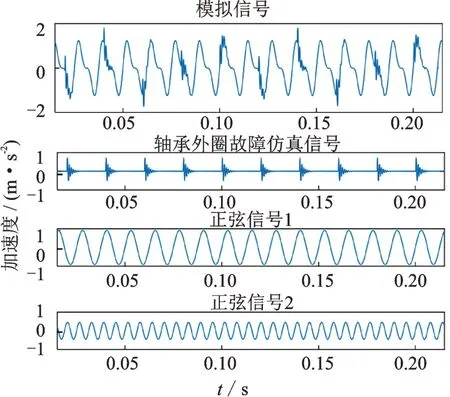
圖2 模擬信號及其組成Fig.2 Simulation signal and its composition

通過公式（6），利用MBCV 法求出該模擬信號頻域的閾值TH，如圖3所示。

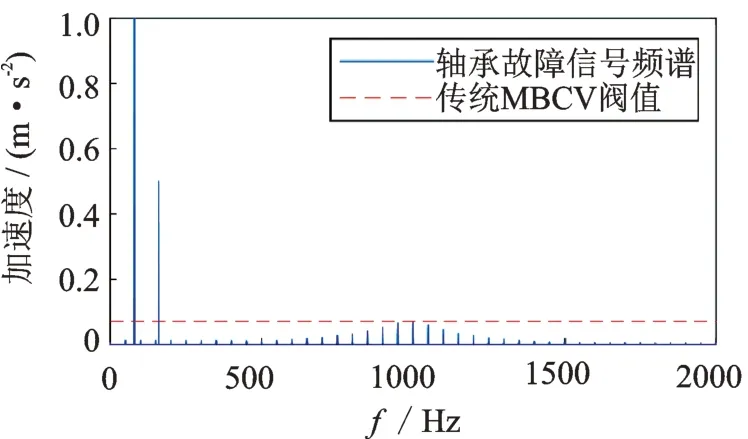
圖3 傳統MBCV 法的分割閾值Fig.3 Segmentation threshold of traditional MBCV method

閾值TH將整個頻域分為高低兩部分，分別將這兩部分做逆傅里葉變換實現信號分離，分離結果如圖4所示。

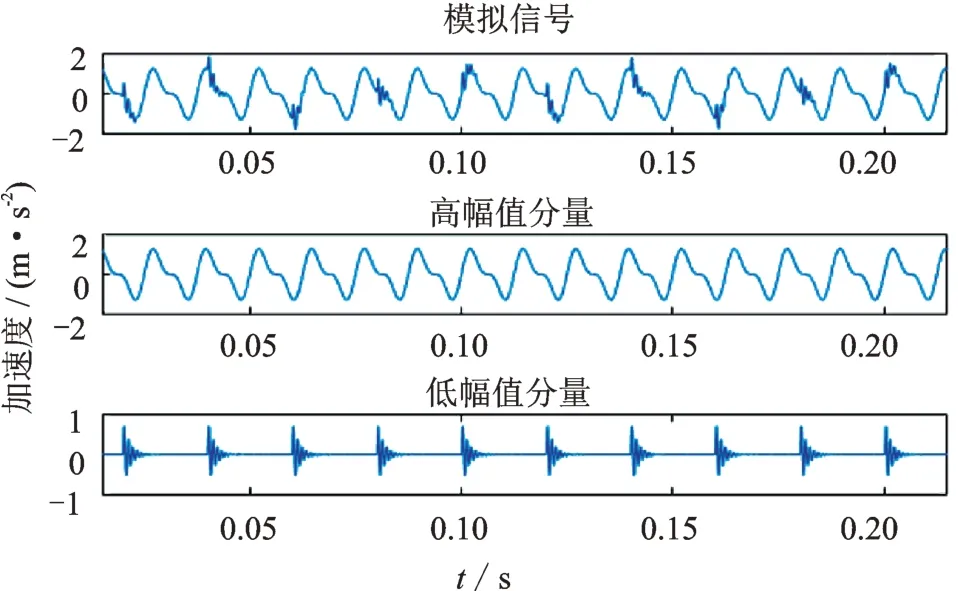
圖4 模擬信號分解結果Fig.4 Simulation signal decomposition results

從圖中可以看出，MBCV 法成功地從模擬信號中分離出軸承外圈故障信號。然而，對于工程實際信號來說，由于信號的組成和峰值情況未知，往往需要重復多次上述步驟才能分離出故障信號。而且，由于分離次數無法預測，需要耗費大量人力進行調試，效率低而且不夠準確。為了解決這一問題，提出一種基于改進MBCV 法的滾動軸承故障診斷方法。

2 基于改進MBCV 算法的軸承故障診斷方法

2.1 改進MBCV 閾值

針對傳統MBCV 法對工程實際信號的診斷效果較差甚至失效這一問題，進行了深入的研究。傳統MBCV 法能實現信號分離的關鍵在于最大類間方差閾值的分類效果。由最大類間方差的定義可知，該閾值是一種針對整個頻域的統計學閾值，而且是定值。然而，軸承故障信號的故障信息通常集中在某一頻段中，這種針對整個頻域的閾值無法準確提取出軸承故障信息。因此，要想達到最優的分離效果就要使閾值能在保留軸承故障信息的同時，最大程度地去除離散頻率成分。

為了實現這一目標，本文對MBCV 法的閾值確定方法進行了改進。主要思路是將原來的全局閾值改為局部動態的閾值曲線，增強閾值的細節分辨能力，從而提高信號分離的準確率。具體步驟如圖5所示。

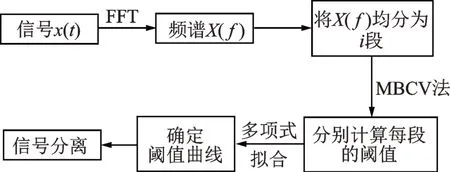
圖5 閾值改進步驟Fig.5 Improved threshold steps

即先將信號頻譜均分為i（i>1）段，分別計算每段頻域內的最大類間方差閾值，最后使用多項式插值法對所有閾值進行擬合，以擬合的閾值曲線代替原來的固定閾值。

2.2 確定最優閾值曲線

閾值曲線相較于傳統的固定閾值對軸承故障信號的分離更加準確，更適合實際的軸承信號提取。但是，要想達到最優的分離效果就要使閾值曲線能在保留軸承故障信息的同時，最大程度地去除離散頻率成分。對于實際采集的信號，由于其構成成分復雜、各成分峰值情況未知，無法直接確定最優閾值曲線。因此，有必要對最優閾值曲線的確定方法做進一步研究。

均方根誤差能用來衡量預測值同真值之間的偏差。在軸承故障診斷中，可以通過計算最后的分離信號與原軸承故障信號之間的均方根誤差來判斷分離信號是否準確。均方根誤差越小說明信號分離越準確。基于這一事實，提出了挑選最佳閾值曲線即確定分割段數i的方法，具體流程如下：

（a）求出信號x(t)頻譜X(f)，并設置最大分割段數S，將X(f)均分為i段（i=2，3，4，…，S）；

（b）當i=2 時，根據改進的MBCV 算法分離出低振幅信號xi(t)，并求出該分量與原軸承故障信號的均方根誤差RMSE；

（c）令i=i+1，返回步驟（b），開始新一輪計算，直至i>S時結束；

（d）對均方根誤差數據集進行趨勢擬合，均方根誤差最小時對應的分割段數i最優，即此時的閾值曲線最佳。

2.3 診斷流程

在上述研究的基礎上，提出了基于改進MBCV算法的軸承故障診斷流程，流程圖如圖6所示。

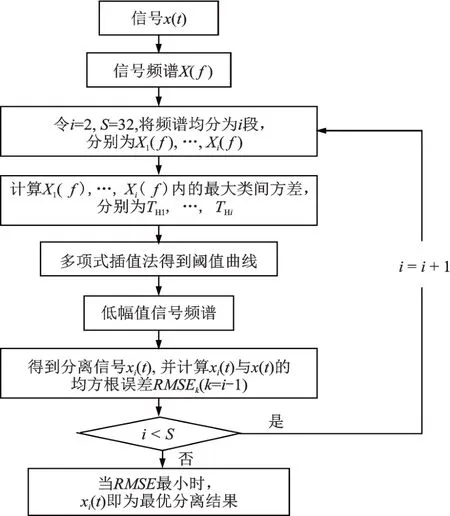
圖6 改進MBCV 法的軸承故障診斷流程Fig.6 Bearing fault diagnosis flow based on improved MBCV method

3 實驗驗證

3.1 案例1

采用美國辛辛那提大學實驗中心在2003～2004年進行的軸承壽命實驗數據進行研究，實驗裝置如圖7所示。電動機轉速保持在2000 r/min，通過傳送帶和軸連接，軸上安裝了四個Rexnord ZA?2115 滾動軸承，軸承每排有16 個滾子，節距直徑2.815 in，滾子直徑0.331 in，接觸角15.17°，軸和軸承承受6000 lb（約26690 N）的徑向載荷。在軸承座上安裝了PCB 353B33 高靈敏度石英加速度計，采樣頻率20 kHz，每隔10 min 采集一次，直至軸承1 外圈出現嚴重損傷停機。本文只使用了在第一軸承殼體上采集到的振動信號，利用軸轉頻率和軸承幾何形狀計算了滾動軸承的特性缺陷頻率。這些頻率值如下：滾動體故障特征頻率fBSF=139.92 Hz，保持架故障特征頻率fBFF= 279.84 Hz，外圈故障特征頻率fBPFO=236.40 Hz，內圈故障特征頻率fBPFI=296.93 Hz。

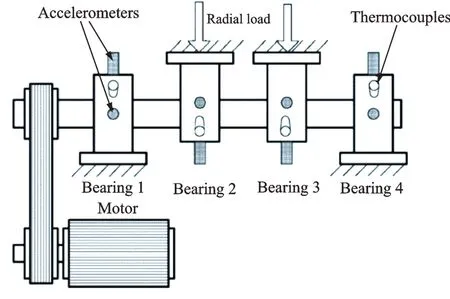
圖7 辛辛那提大學軸承實驗臺系統Fig.7 The bearing experimental platform system of Univer?sity of Cincinnati

由于該數據是在實驗臺上采集的，為了模擬實際工作環境，在每個軸承信號中都加入正常運行模擬變速箱信號，該信號由下式產生：

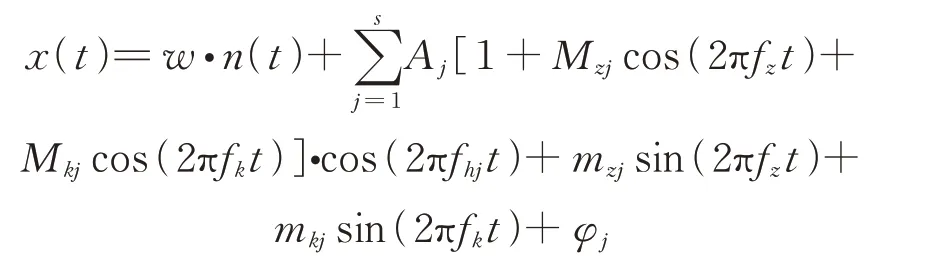
式中fz為電機轉軸的轉頻，fk為齒輪轉頻，s為齒輪嚙合頻率的諧波倍頻，Aj為第j個齒輪嚙合諧波的幅值，Mzj為第j階與軸頻相關的幅值調制系數，Mkj為第j階與齒輪轉頻相關的幅值調制系數，fhi為第j階齒輪嚙合諧波頻率，mzj為第j階與軸頻相關的相位調制系數，mkj為第j階與齒輪轉頻相關的相位調制系數，φj為第j階相位角，n（t）為符合高斯分布的隨機噪聲，w為噪聲幅值系數。

具體參數見文獻［11］，該實驗信號如圖8所示。

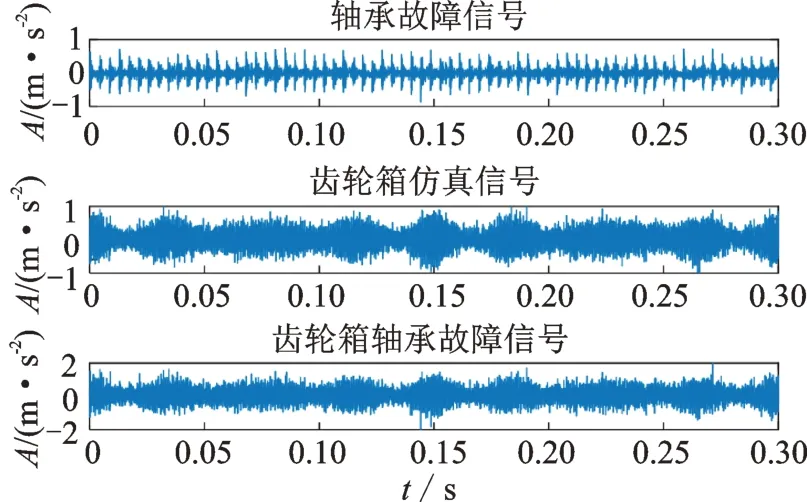
圖8 齒輪箱軸承故障信號時域圖Fig.8 Time domain diagram of gearbox bearing fault signal

依據本文提出的診斷方法，對該信號進行處理。首先，預設頻域最大分割段數S=32；然后，分別求出各分割段數情況下低幅值分量與軸承故障信號的均方根誤差，并繪制離散圖；最后，對該離散圖進行多項式擬合并觀察趨勢，結果如圖9所示。

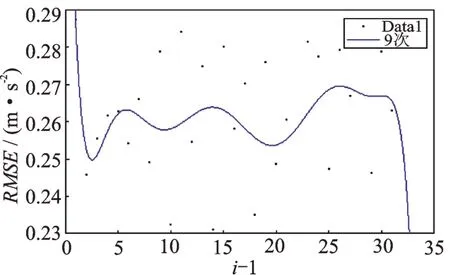
圖9 均方根誤差散點圖及其趨勢Fig.9 Root mean square error scatter plot and its trend

由圖9可知，在排除末尾項后，當i=4 時，均方根誤差出現首個極小值且為最小值。因此認為將頻譜分為四段時求得的閾值擬合曲線能最大程度地分離出故障信號。

此時，其最優閾值擬合曲線結果如圖10 所示。將閾值曲線與原方法得到的閾值進行對比，不難發現改進后的方法對軸承信息的提取效果更好。

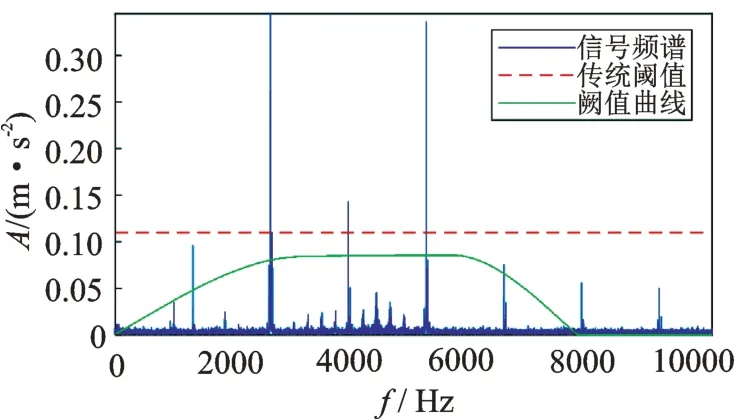
圖10 改進方法的閾值曲線和傳統方法的固定閾值Fig.10 Improved threshold curve and traditional fixed threshold

求出此時對應的低幅值信號x4(t)，直接對x4(t)進行平方包絡分析，包絡譜如圖11 所示。從圖中可以清晰地診斷出軸承故障頻率。同時，為了驗證該方法的優越性，將其與原方法的結果進行對比。對比發現，改進后的方法要比原方法的分離效果更好，診斷結果更加準確。

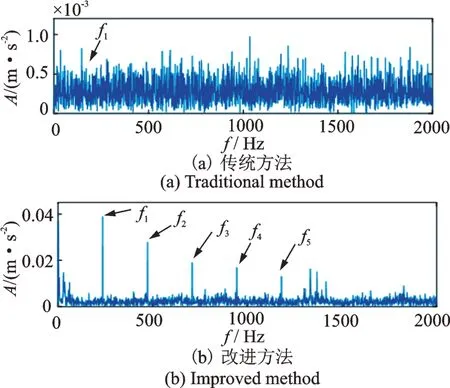
圖11 診斷結果Fig.11 Diagnosis results

3.2 案例2

采用美國凱斯西儲大學軸承內圈故障數據進行驗證。實驗系統如圖12 所示，左側為一個1.5 kW的電動機，右側為一個功率測試計。軸承型號為SKF6205，軸轉速為1750 r/min，采樣頻率為12 kHz，損傷直徑為0.028 in。為了充分驗證改進方法的優越性，在采集的軸承故障信號中加入信噪比為10 的白噪聲，該信號如圖13 所示。

圖12 凱斯西儲大學實驗臺系統Fig.12 The bearing experimental platform system of Case Western Reserve University

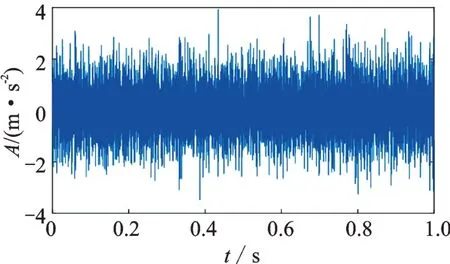
圖13 軸承內圈故障信號Fig.13 Bearing inner race fault signal

使用改進MBCV 法對該軸承故障信號進行分析。同樣，預設最大分解段數S=32，繪制出均方根誤差散點圖和趨勢圖，如圖14 所示。

由圖14 可知，當i=12 時，均方根誤差首次由下降變得平穩，此時獲得的閾值擬合曲線最佳，該最優閾值曲線如圖15 所示。

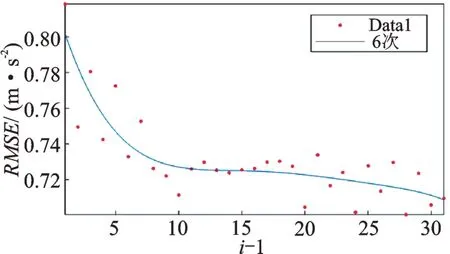
圖14 均方根誤差散點圖及其趨勢Fig.14 Root mean square error scatter plot and its trend

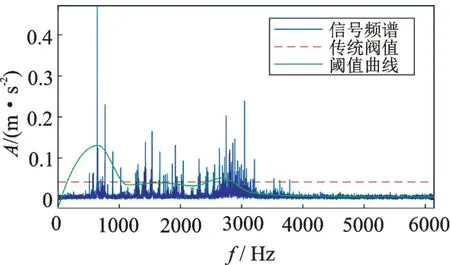
圖15 改進方法的閾值曲線和傳統方法的固定閾值Fig.15 Improved threshold curve and traditional fixed threshold

圖中紅色虛線為傳統MBCV 方法計算出的固定閾值。分別使用改進方法和傳統方法對此信號進行處理，結果如圖16 所示。由圖16 表明，相比原方法改進方法的診斷結果更加清晰準確。

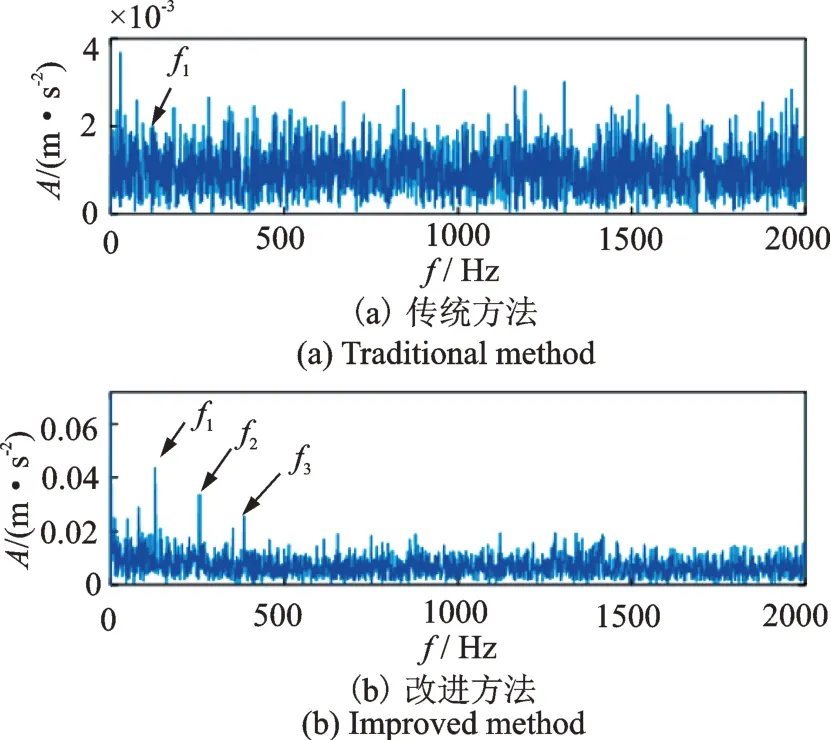
圖16 診斷結果Fig.16 Diagnosis results

4 結 論

（1）本文針對傳統MBCV 方法的不足，提出了一種基于改進MBCV 法的軸承信號分離方法。該方法使用動態閾值擬合曲線代替傳統的固定閾值。實驗結果表明，閾值曲線增強了局部分辨率，提高了信號分離的準確率。

（2）將改進的MBCV 法應用于軸承故障診斷中。同時，根據軸承故障信號的特點提出了選取最優閾值曲線的方法。通過仿真及實驗分析驗證了該方法的有效性。由于該方法基本不需要人為設定參數，比較適合于工業上的自動檢測系統，具有較強的實用價值。