雙腔室空氣彈簧動剛度理論模型與實驗研究
鄔明宇,李雪冰,尹 航,呂靖成,危銀濤
(清華大學車輛與運載學院,北京 100084)
1 概 述
帶附加氣室的空氣彈簧以其優良的隔振性能,已經在車輛領域(乘用車、地鐵、高速鐵路等)得到了普遍應用[1]。對于乘用車來說,空氣彈簧具有可調高度、質量較輕、承載能力高、可有效抑制噪聲等優點[2]。圖1展示了乘用車的帶附加氣室膜式空氣彈簧系統初始狀態及定質量工作過程原理圖,該系統主要包括主要承載力的空氣氣囊、用于調節剛度的附加氣室、充氣用的儲氣罐以及相關管路等零部件。在過去的半個世紀對車輛用空氣彈簧動力學的研究層出不窮,主要方法有幾何學法、等效力學模型、熱力學等。
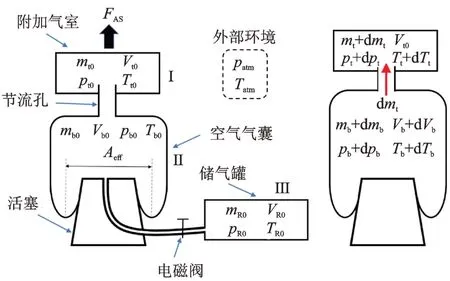
圖1 空氣彈簧充放氣及定質量工作原理圖Fig.1 The working principle diagram of air spring
Bruni 等[3]對空氣彈簧的動力學模型進行詳細總結。典型的動力學模型包括在一定頻率下適用的Nishimura model[4],Simpack model[5],考慮平方阻尼項的Vampire model[6],考慮摩擦單元與速度指數項相關阻尼的Berg model[7]以及一些相應的改進模型[2,8]。Quaglia等[9]推導出一個非線性模型,分析了該模型的頻率特性和階躍響應,并利用線性模型討論懸架剛度特性。Zhu等[10]推導出了帶附加氣室的空氣彈簧的動態剛度,并通過實驗進行了理論驗證。LIU 等[11]研究了空氣彈簧受諧波位移激勵時動態剛度隨腔室之間連接孔面積的變化,并進行仿真和實驗驗證。Li等[12]基于幾何學對鐵路用空氣彈簧進行垂向剛度建模,并進行實驗分析和參數討論。除此之外,Li等[13]還將氣體變化過程假設成多變過程并進行仿真分析,為后續深入了解空氣氣囊氣體變化過程提供了一定的思路。Lee 等[14]基于Harris 等[15]和Bryan[16]的工作,利用熱力學、連接管路模型建立雙腔室空氣彈簧動力學特性,并分析氣體的振蕩過程,為后續熱力學建模提供了一定的思路和參考。Facchinetti等[17]研究了空氣彈簧剪切和側傾變形之間的準靜態耦合效應對車輪/鐵路接觸力的影響,對行駛安全性和平順性提升有一定指導意義。Docquier[18]基于多體動力學和氣體動力學對鐵路用空氣懸架系統進行建模,并進行了懸架的結構優化。除此之外,Docquier 等[19]對熱交換過程進行敏感性分析,并深入研究了雙腔室空氣彈簧內部的多變過程,研究表明車輛的動力學特性與熱交換率有很強的相關性,對后續建模有一定指導意義。Yin 等[20]提出了一種結構空氣彈簧,利用氣體多變過程推導出動力學模型并以實驗進行驗證。李芾等[21]對空氣彈簧動力學參數進行分析,得出不同參數對空氣彈簧動力學特性的影響。陳俊杰等[22]利用線性模型以及試驗參數辨識方法對空氣彈簧關鍵設計參數進行標定研究。目前對空氣彈簧動剛度研究主要是基于氣體多變或絕熱假設進行推導,而沒有從熱力學角度出發推導考慮能量耗散的帶附加氣室空氣彈簧的動剛度公式。本文基于熱力學第一定律,應用空氣動力學、結構動力學理論推得一套適用于雙腔室空氣彈簧的動力學模型,并給出各項明確的物理意義及數學表達。
本文結構主要分為以下三個方面。首先,基于熱力學第一定律、空氣動力學、結構動力學提出了一組考慮能量耗散的多腔室空氣彈簧動力學方程及具有物理特性的抽象模型;其次,針對連接孔較大(不考慮連接孔阻尼)情況進行了理論簡化并設計實驗;最后,利用仿真方法進行了線性剛度、非線性剛度、考慮阻尼特性的動剛度公式與實驗結果的對比。結果表明,本文提出的動剛度公式能在大行程范圍內很好地擬合空氣彈簧的動力學行為,解釋空氣彈簧剛度非線性及其滯回特性。
2 帶附加氣室空氣彈簧動剛度模型
帶附加氣室的空氣彈簧動剛度模型主要基于熱力學第一定律推導出各氣室的能量交換方程;結合空氣動力學理論給出氣室間連接孔的質量流量方程;最后結合四分之一懸架動力學方程進行合理假設和傅里葉變換,給出動剛度各部分貢獻項的物理意義及數學表達。
2.1 熱力學方程
帶附加氣室空氣彈簧氣動圖如圖1所示,在結束充放氣后空氣彈簧內部氣體質量就確定了。這里首先對全文參數及正方向進行定義:m,p,V,T分別代表質量、壓強、體積和熱力學溫度,下標b,t,R代表空氣氣囊、附加氣室和儲氣罐。壓強為絕對壓強;氣體質量流量以流入附加氣室為正;氣體壓強、溫度、質量、體積變化量以變大為正;位移、力向上為正。對空氣取理想氣體狀態常數R= 287 J/(kg ?K),比熱容比γ= 1.4。并有氣體狀態方程及其全微分恒成立,熱力學第一定律恒成立,分別以從外界吸熱、外界對氣體做功和內能增加為正。即:
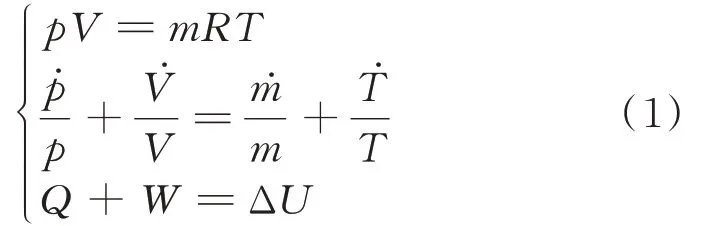
根據氣動圖建立附加氣室和空氣氣囊部分的熱力學第一定律方程。對Ⅰ(附加氣室)列寫熱力學公式,由于附加氣室體積不變,故外界對附加氣室做功為零。根據氣體流向正方向定義,對附加氣室內能部分第一項取負值代入熱力學第一定律方程(1)中,并除以時間步長dt,得到:
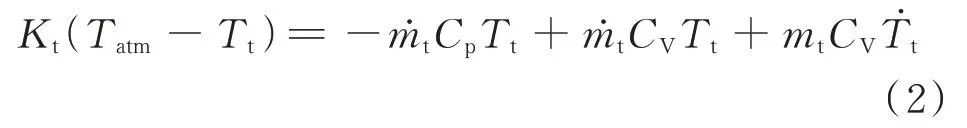
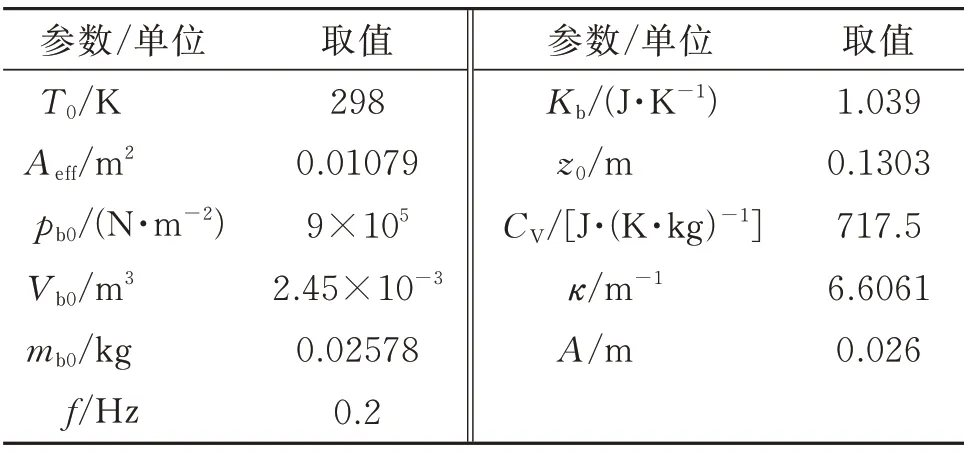
式中Kt為與外界熱交換系數,Tatm為外界大氣溫度,Cp為定壓比熱容,CV為定容比熱容。
結合式(2)與氣體狀態方程微分形式(1)消去該氣室溫度的導數,根據熱力學定律得出的氣體質量流量表達式為:
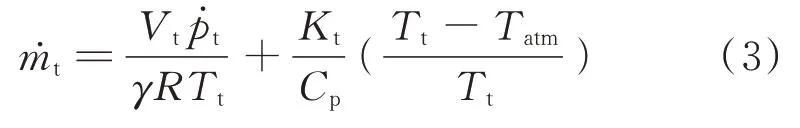
同理,假設連接在附加氣室與氣囊之間的管道很短,無質量滯后。對Ⅱ(氣囊)列寫熱力學公式,消去溫度隨時間的導數得:
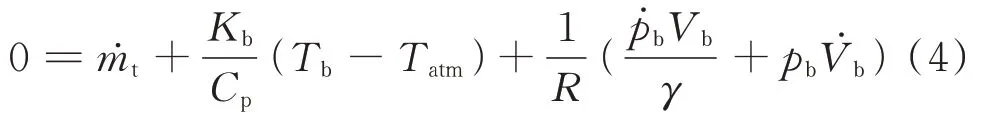
帶附加氣室的空氣彈簧熱力學方程由式(3),(4)進行表述。需要說明的是,該方程在進行推導的時候未規定附加氣室腔室個數,故對多腔室的空氣彈簧仍適用。下面根據空氣動力學理論推導出連接孔兩側壓強與質量流量之間的關系。
2.2 空氣動力學方程
根據空氣動力學理論[14]對小孔流動的描述以及氣體狀態方程,并且考慮對連接孔的有效面積進行系數修正,對不同壓強根據氣體流向正方向定義得出質量流量為:
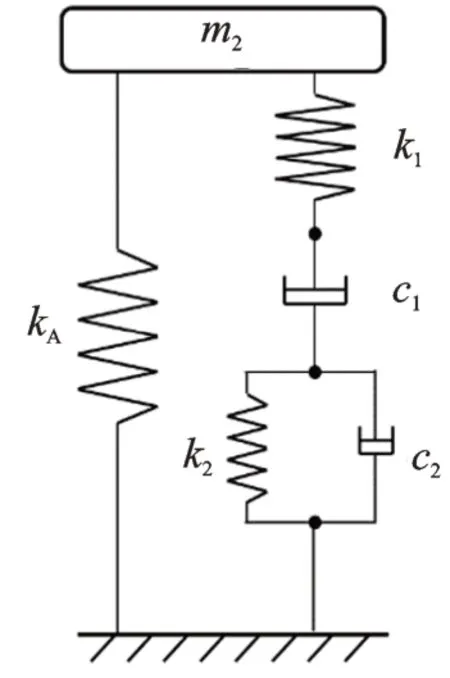
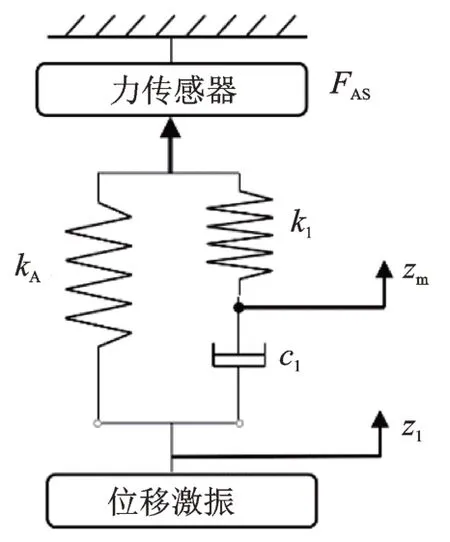
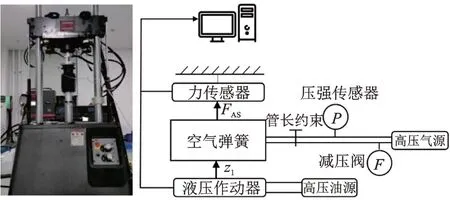
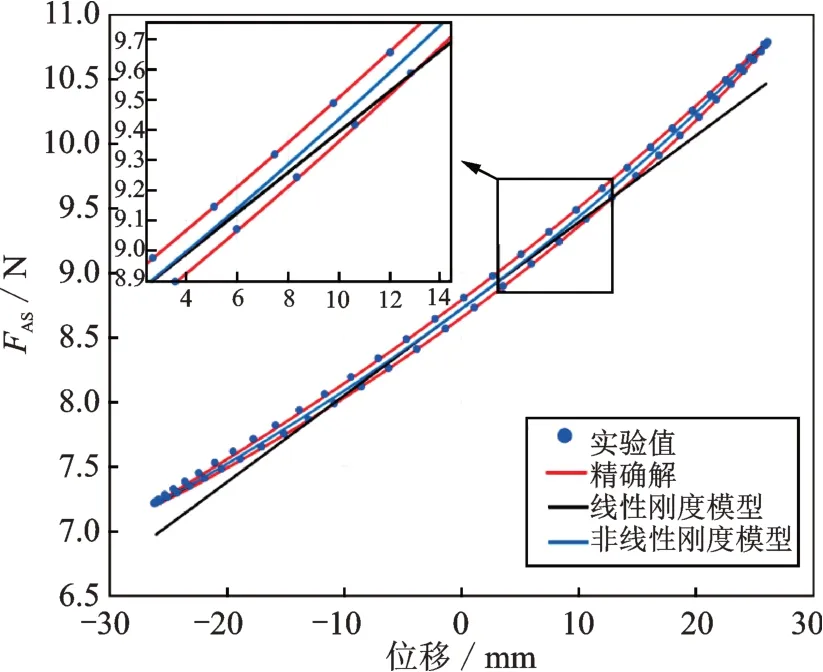
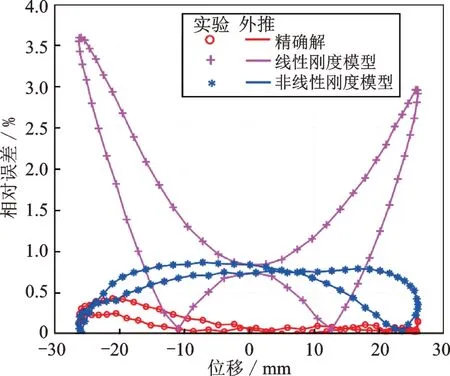
當pt 當pt>pb時, 為了使后續建模的過程中避免對不同腔室之間的氣體進行分類討論,本文引入一些假設,在不改變空氣動力學本質的基礎上通過數學技巧進行模型化簡。首先根據實際情況,雙腔室空氣彈簧氣囊與附加氣室之間的壓強比應當大于0.5283。并取α=min {pb,pt}/max {pb,pt} ≤1。 進而做假設如下: 式中T0為初始狀態溫度。 將式(6)代入(5),進而可以用一個等式來表示不同情況下空氣氣囊與附加氣室之間的氣體質量流量公式: 在確定了附加氣室與空氣氣囊之間連接孔的面積之后,δ(α)就是壓強比的函數。利用該公式可以將需要分類討論的兩種情況進行合并分析。下面結合動力學模型進行帶附加氣室空氣彈簧模型的構建。 如前所述,在充放氣過程結束后,整個空氣彈簧帶附加氣室內部氣體總質量就確定了,下面根據前述熱力學方程及空氣動力學方程推導出四分之一空氣懸架的動力學模型。圖2為根據車輛四分之一懸架簡化后的模型,空氣彈簧視為彈性元件。 圖2 四分之一空氣懸架模型Fig.2 One-quarter air suspension model 首先需要指出的是,空氣懸架系統具有高度可調的特性,理論上來說可以在任何初始位置保持平衡狀態。這是區別于傳統被動彈簧的重要特征。也是由于這個特征,在列寫動力學方程式的時候就不能用結構動力學的一般方法(如牛頓第二定律或拉格朗日第二定律等)以重力導致的靜止狀態為初始平衡位置列寫動力學方程。所以,本文中對空氣懸架系統動力學方程的建立均建立在考慮所有重力的基礎上。由結構動力學知識可知,對圖2所示二自由度動力學系統,其動力學方程組為: 需要注意的是式(8)中空氣彈簧傳遞的力特性公式是顯然成立的。其全微分為: 由此看出有效面積變化以及壓強變化均會對力學傳遞特性有重要影響。后文先基于有效面積不變假設展開,在最后給出考慮有效面積變化時的動剛度公式。 通過式(3),(4),(7)以及(8),將流經節流孔的氣體質量流量消去。又因為空氣氣囊與外界接觸面積比附加氣室大,故不考慮附加氣室與外界的熱量交換(或者可以考慮此熱量通過空氣氣囊與空氣進行熱交換)。得到: 再對空氣氣囊溫度與外界大氣溫度差、壓強與空氣氣囊速度耦合項、空氣懸架系統的行程倒數與原初始高度倒數進行假設: 式中z1為簧下位置位移,z2為簧上位量位移,h0為初始狀態懸架高度,下標0 表示初始狀態。 將式(11)代入(10)中得到簡化后的空氣彈簧參數間的微分關系: 在式(12)中有時域變量:pt,pb,(z2-z1)和FAS,對時域變量進行傅里葉變換。又基于式(8)力學傳遞特性的傅里葉變換及懸架動行程Z(ω)=Z1(ω)-Z2(ω),式(12)變為: 消去附加氣室壓強傅里葉變換可得附加氣室與懸架動行程之間的頻域關系。根據動力學系統的正方向定義,結合式(13),帶附加氣室的空氣彈簧總動剛度計算公式可以表示為: 觀察式(14),擬將其整理成具有物理意義的剛度公式。為此,對其進行簡單數學變換如下: 式中ω為激勵圓頻率,j 為虛數單位, 在等效完之后的動剛度表達式中,從動力學等效角度可以將其視為如下三項的串聯形式:彈簧k1、阻尼器c1、彈簧k2和阻尼器c2的并聯系統。仍然要強調的是,上述推導并未考慮有效面積的變化以及其變化對空氣彈簧等效動剛度的影響,因為有效面積的變化對空氣氣囊體積的計算影響很小。但根據式(9)可以得知有效面積變化量對剛度的直接影響較大,設由有效面積變化產生的等效剛度為kA,則有: 式中FAS,2代表由有效面積變化對空氣彈簧力學傳遞特性的影響。至此,根據熱力學、空氣動力學、結構動力學推導出的多腔室空氣彈簧的動力學模型可以直觀表示,如圖3所示。 圖3 雙腔室空氣彈簧等效力學模型Fig.3 Equivalent mechanical model of dual-chamber air spring 所以空氣彈簧的等效動剛度可分為假設有效面積不變化時由于熱力學、空氣動力學影響的部分與有效面積變化時對剛度的影響部分。結合式(15)和(17),動剛度總表達式為: 需要注意的是,該模型僅為懸架系統中空氣彈簧部件的等效動剛度公式,實際懸架還存在阻尼器,本文主要聚焦于空氣彈簧的模型建立。 下面對推導出的多腔室空氣彈簧的等效剛度公式(18)進行討論。其中由有效面積變化產生的剛度變化部分為kA;由空氣氣囊部分產生的剛度和阻尼項為k1與c1,兩部分串聯;由附加氣室產生的等效剛度和等效阻尼為k2和c2,與空氣氣囊部分串聯。根據式(16)的c1項可知,由空氣氣囊產生的阻尼項中的參數Kb主要是由空氣氣囊、附加氣室、空氣氣囊的阻尼項三個因素共同影響產生的。這里忽略了由橡膠氣囊產生的剛度部分,因為該部分影響十分小[12],故做忽略的假設是合理的。 本節中推導的創新點主要在于明確了多腔室空氣彈簧等效力學模型中各個元件的物理意義及影響因素,給出了各部件的明確數學表達式。并且基于熱力學第一定律綜合考慮了由附加氣室、空氣氣囊以及橡膠?簾線材料產生的阻尼特性導致的滯回特性。 為了證明本文中提出的帶附加氣室空氣彈簧動力學模型具有普適性,現對其進行簡化,假設附加氣室與空氣氣囊之間的連接孔很大,以至于可以不考慮其阻尼特性[14]。這也與實際情況相符,因為本文的主要對象是乘用車使用的空氣彈簧,其大部分形式為膜式空氣彈簧。單腔室空氣彈簧的動力學分析與雙腔室空氣彈簧類似,僅為除去小孔和附加氣室產生的影響[12]。則式(18)變為: 空氣氣囊動剛度公式的剛度部分與Li 等[12]得出的結論相符。但是從本文中可以看出實際的動剛度應該是動剛度的模,也就是說由于熱交換、氣囊的等效阻尼會使得實際的動剛度比單純考慮氣體的剛度低。下面針對式(19)進行討論分析。根據Qua?glia 等[9]的工作,本文將有效面積隨高度的變化簡化為線性,則可推得由有效面積變化產生的動剛度表達式為: 需要指出的是,式(19)對任意空氣彈簧平衡位置處及小振幅情況下均適用。根據此結論,可以將式(19)進行適當擴展。下面考慮將阻尼仍看不隨高度、有效面積變化的常數。將彈性項k1看不隨有效面積變化而變化,但與當前狀態下壓強和氣室體積有關的變化量,即: 本文主要關心單腔室空氣彈簧的動力學特性及力學傳遞特性,故針對式(21)構造出單腔室空氣彈簧的動力學等效力學模型及原理圖如圖4所示。 由圖4可以列出其力學傳遞特性微分方程: 圖4 單腔室空氣彈簧等效力學模型Fig.4 Equivalent mechanical model of single-chamber air spring 針對式(22),如果假設k1不變,即為最常見的線性模型;如果將其泰勒展開成高度的一階形式則為非線性模型,即: 本文提出的基于非線性剛度和考慮阻尼滯回特性的模型稱為精確解。 本文搭建了MTS 示功實驗平臺,并采用國內某車型使用的后軸空氣彈簧設計工裝以及實驗流程。圖5展示了MTS 及空氣彈簧實驗設備,連接管路采用Φ6 mm 管。利用高壓氣源將空氣彈簧充氣,達到工作的力值后通過減壓閥進行壓強控制。讀出此時的壓強值并約束管長進行實驗。 圖5 空氣彈簧MTS 實驗及原理圖Fig.5 MTS test bench and schematic diagram 實驗數據由MTS 傳感器讀取,包括固定采樣頻率的力傳感器值、液壓作動器位移、作動器速度、記錄時間等數據。下面進行實驗對比及數據分析。 本次實驗采用的參數與空氣彈簧結構參數如表1所示,利用MTS 設備產生正弦激勵波,其表達式為: 根據表1及公式(16)可以得到線性模型、非線性模型,利用Simulink 將本文中提出的考慮滯回特性的精確解進行仿真并與實驗進行對比,結果如圖6所示。 圖6 實驗結果與理論對比Fig.6 Comparison of experimental and theoretical results 表1 實驗參數及取值Tab.1 Experimental parameters and values 可以看出,線性剛度公式在一定小振動幅度范圍內(約±5 mm 左右)可以較好地擬合空氣彈簧動力學行為,但是隨著振幅加大,擬合效果逐漸變差。非線性剛度公式可以在較大振幅范圍內對空氣彈簧的動力學行為進行描述,但是其缺點是無法反映空氣彈簧加載卸載的滯回特性。不同設計或工況下空氣彈簧的滯回特性可能十分顯著,本例中取實驗值在初始坐標范圍附近,其加載、卸載的差值約為150 N,如果忽略此差值可能會對后續動力學模型及整車動力學行為的仿真造成影響。從本文提出的考慮空氣彈簧熱交換、橡膠阻尼的精確解曲線可以看出其能精確描述空氣彈簧在運動過程中的滯回特性及動力學行為,與實驗吻合程度較高。下面針對不同理論公式與實驗結果進行比較,并給出誤差量化指標的計算公式。本文中采用的是不同模型與實驗的相對誤差的絕對值,其計算公式為: 三種模型的理論解與實驗值的比較及合理外推值如圖7所示。 圖7 不同模型相對誤差比較Fig.7 Comparison of relative errors of different models 可以看出線性模型的誤差最大,在振幅最大值時預測誤差超過3%;非線性模型比線性模型精度高,且在中間位置誤差較大,振幅最大值處誤差較小;本文給出的精確解精度最高,不論位移大小其相對誤差均可以控制在0.5%以內。故可以得出結論,本文提出的多腔室空氣彈簧動剛度解析計算公式具有較高的精確性,可以適用于空氣懸架的精確控制。 提出了一種考慮空氣氣囊熱交換與阻尼滯回特性的多腔室空氣彈簧動力學模型,并進行了實驗驗證;給出了對應等效力學模型的各部分明確的物理意義及數學表達式,論文結論如下: 1)所提出的多腔空氣彈簧模型推導過程中未限制氣體狀態變化,故具有較強的普適性; 2)搭建了空氣彈簧動態特性試驗臺架,實驗比較了線性模型、非線性模型、和本文的精確解,證實了考慮滯回特性的精確解模型可以很好地反映空氣彈簧的動力學特性,在大行程下與實驗值的相對誤差小于0.5%。 本文提出的多腔室空氣彈簧動剛度模型對后續懸架精確控制及整車仿真和實驗驗證提供了很好的基礎。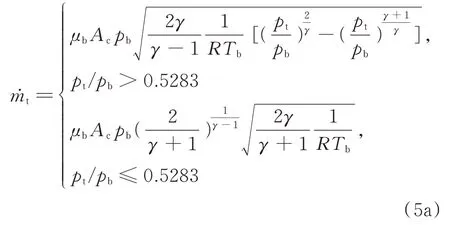
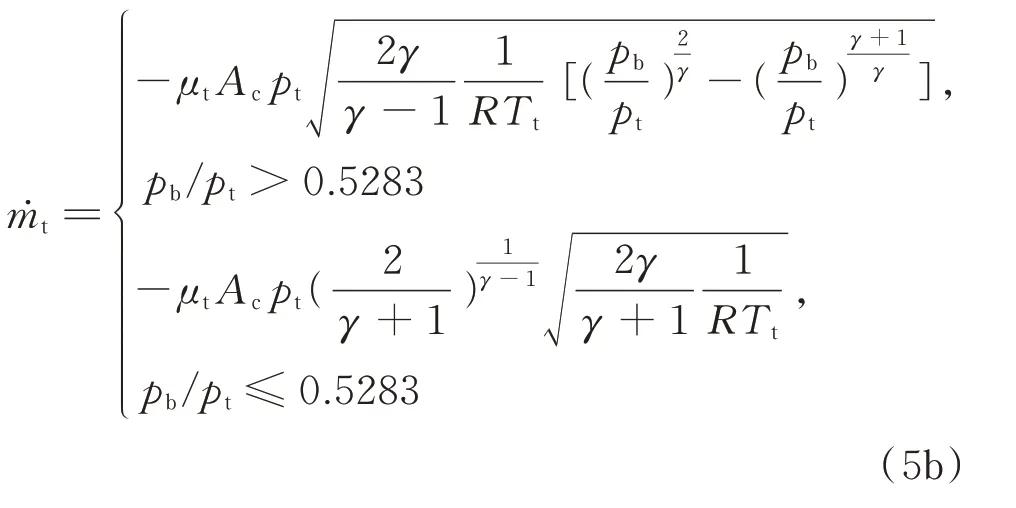
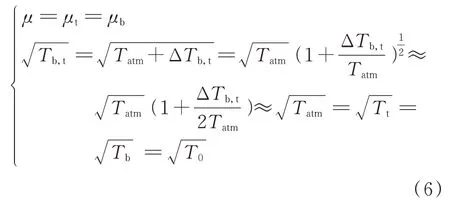
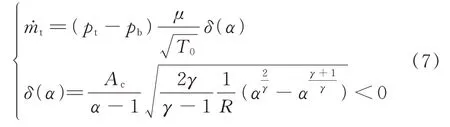
2.3 動力學模型

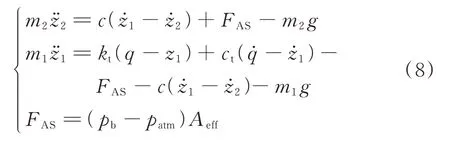
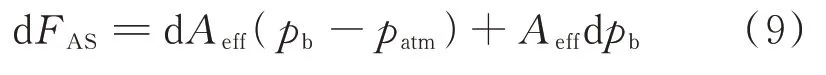
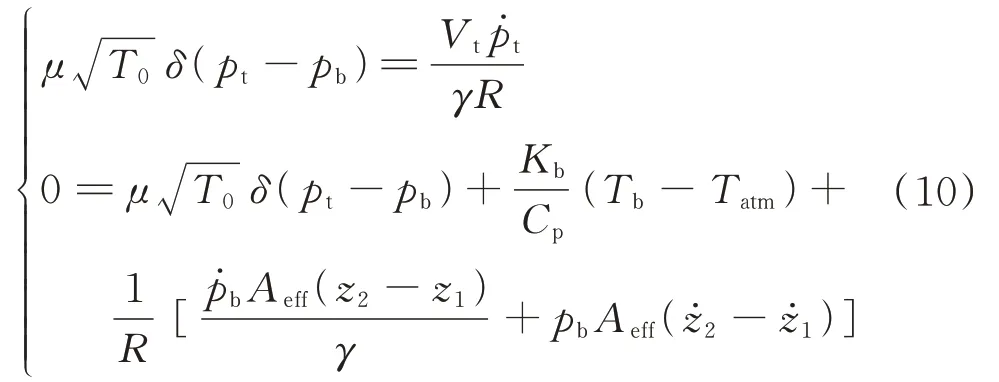

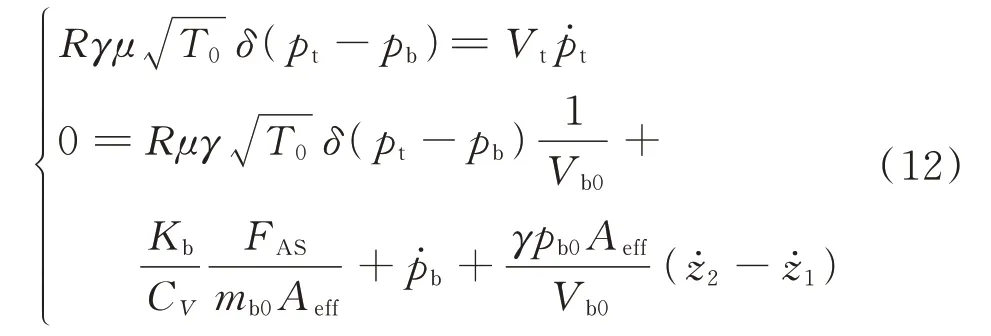
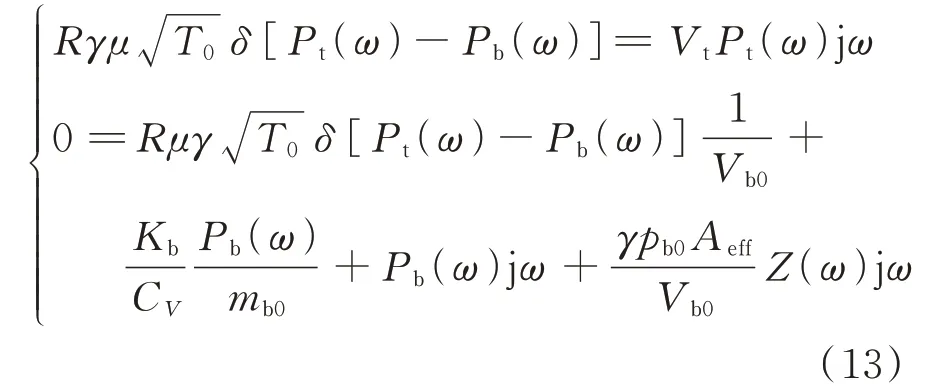
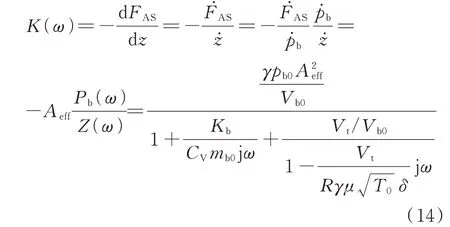
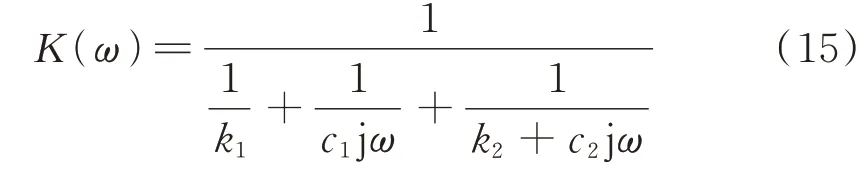
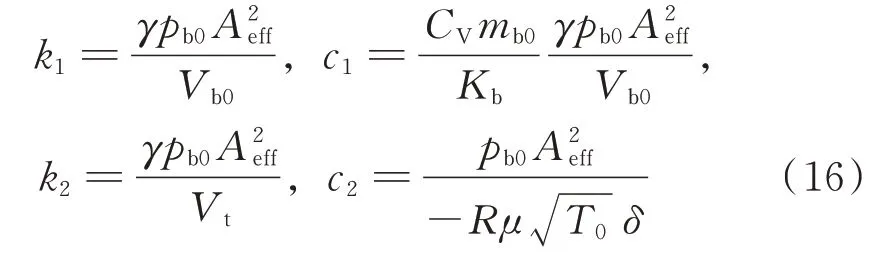
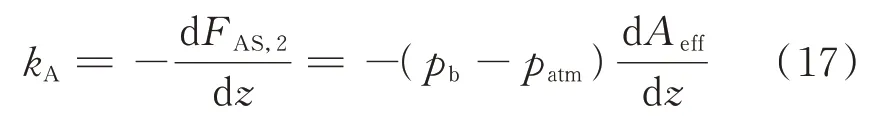
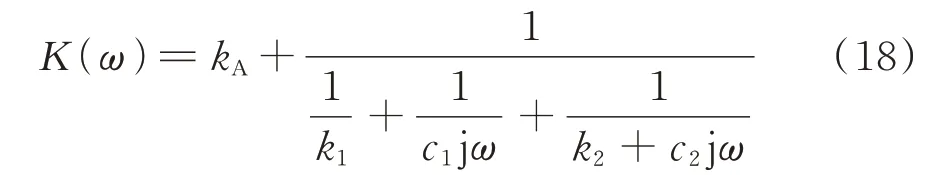
3 模型簡化及實驗設計
3.1 不考慮連接孔阻尼的空氣彈簧力學特性簡化

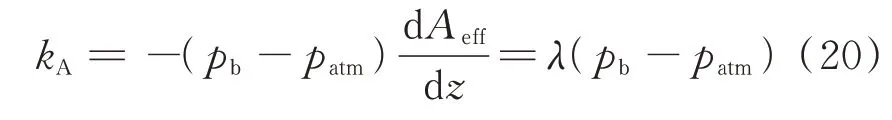
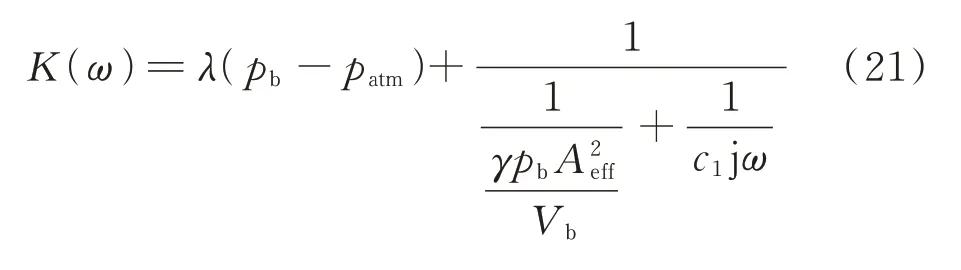
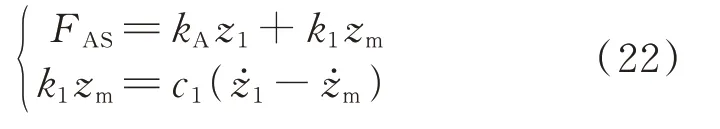
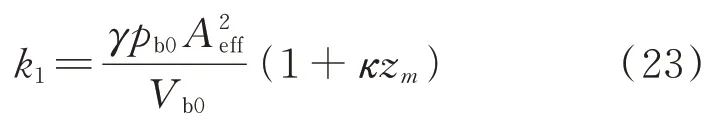
3.2 實驗設計
4 實驗對比及數據分析
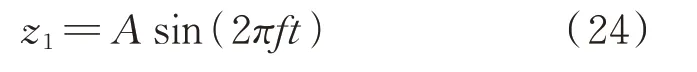
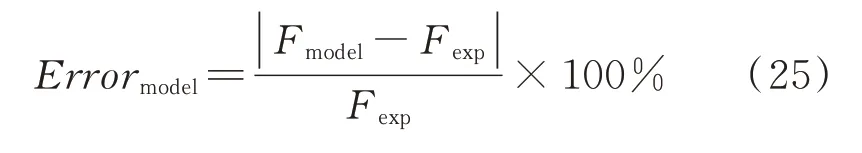
5 結 論

